Что такое frac в математике
Вещественные числа
Вещественные, или действительные, числа — это, грубо говоря, и целые и дробные. Они, конечно, нередко возникают в задачах, но при работе с ними возникают серьезные проблемы, которые не в каждой книге по программированию будут описаны.
Как компьютер хранит вещественные числа?
(Если вы не поймете, что написано в этом разделе, это не очень страшно, но попробуйте понять.)
Вещественные числа, с которыми может иметь дело компьютер, могут быть как очень большими, так и очень маленькими. С другой стороны, вещественные числа в принципе невозможно хранить абсолютно точно, т.к. в них могут быть очень много знаков (даже бесконечно много) после запятой.
Еще более точно — компьютер хранит числа в двоичной системе счисления; все примеры выше сделаны в десятичной системе только для простоты.
Типы данных
Все современные компьютеры умеют работать со следующими тремя типами данных:
5000, занимает в памяти 10 байт, работает намного медленнее;
Эти типы поддерживаются процессором (т.е. процессор умеет выполнять команду «сложить два числа типа single» или «вычесть два числа типа extended» и т.п.). Поэтому эти типы присутствуют (возможно, с другими названиями) во всех существующих языках программирования.
В питоне нет простой возможности выбрать один из этих трех типов, по умолчанию доступен только тип double, причем в питоне он называется float (!).
Про вывод подробнее
Часто в наших задачах вы можете встретить фразу «выведите ответ с точностью до 5 знаков после запятой», или «с пятью верными знаками» и т.п. Такие фразы почти всегда обозначают, что ваш ответ должен содержать 5 верных цифр после запятой, но они не запрещают вам выводить больше цифр. Вы можете вывести хоть 20 цифр — если первые пять из них верные, то ответ будет зачтен. И наоборот, вы можете вывести меньше цифр — если невыведенные цифры — нули, то ответ тоже будет зачтен. Вообще, строго говоря, такая фраза в условии просто обозначает, что ваш ответ должен отличаться от верного не более чем на 1e-5.
Пример: если правильный ответ на задачу — 0.123456789, то вы можете вывести 0.12345, или 0.123459876, или даже 1.2345e-1 (т.к. это то же самое, что и 0.12345). А если правильный ответ — 0.10000023, то вы можете вывести 0.10000, 0.10000987 или даже просто 0.1 или 1e-001 (т.к. это то же самое, что и 0.10000).
В частности, это обозначает, что вы можете пользоваться стандартными функциями вывода (writeln и print) без каких-либо особых ухищрений; не надо округлять число, не надо форматировать вывод и т.д.
Вот если в задаче строго сказано «вывести ровно с 5 знаками после запятой», то это другое дело. Но на приличных олимпиадах такое бывает очень редко.
Полезные функции
Пример программы, используйющей эти функции:
Погрешности
Два правила работы с вещественными числами
Сначала напишу два главных правила работы с вещественными числами:
Ниже я разъясняю оба этих правила.
Необходимость использования eps
Как уже говорилось выше, компьютер не может хранить все цифры числа, он хранит только несколько первых значащих цифр. Поэтому, если, например, разделить 1 на 3, то получится не 0.33333. (бесконечно много цифр), а, например, 0.33333333 (только несколько первых цифр). Если потом умножить результат обратно на 3, то получится не ровно 1, а 0.99999999. (Аналогичный эффект есть на простых калькуляторах; на продвинутых калькуляторах он тоже есть, но проявляется сложнее.)
Поэтому если вы напишите, например, следующий код:
| (для питона такой простой пример у меня подобрать пока не получилось, но в более сложных примерах есть аналогичные проблемы.) |
На самом деле все еще хуже: компьютер работает в двоичной системе счисления, поэтому даже числа, в которых в десятичной системе счисления конечное число цифр, в компьютере могут представляться неточно. Поэтому, например, сравнение if 0.3+0.6=0.9 тоже не сработает: если сложить 0.3 и 0.6, то получится не ровно 0.9, а слегка отличающее число (0.899999 или 0.900001 и т.п.)
(На питоне все тут проявляется еще ярче: print(0.3+0.6) выводит у меня 0.8999999999999999.)
Итак, погрешности, возникающие при любых вычислениях, — это основная проблема работы с вещественными числами. Поэтому если вам надо сравнить два вещественных числа, то надо учитывать, что, даже если на самом деле они должны быть равны, в программе они могут оказаться не равны.
Итак, именно поэтому
(Первое правило будет дальше 🙂 )
* за исключением случаев, когда вам не важно, что произойдет в случае точного равенства, см. ниже.
Выбор eps
Но обычно считают, что в «разумных» задачах все-таки такое eps существует, т.е. числа, которые должны быть равны, отличаются не очень сильно, а те, которые должны отличаться, отличаются намного сильнее. И eps выбирают где-нибудь посередине. (В частности, поэтому, как говорилось выше, не бывает так, что x=y-eps точно.) (В более сложных задачах может понадобиться применять более сложные техники, но мы их сейчас не будем обсуждать.)
Но бывают задачи, где так просто вычислить подходящее eps не получается. На самом деле таких задач большинство — как только вычисления у вас становятся сложнее чем сложить два числа, за погрешностями уже становится сложно уследить. Можно, конечно, применять какие-нибудь сложные техники, но обычно принято просто брать какое-нибудь eps порядка 1e-6..1e-10.
В частности, поэтому на олимпиадах очень не любят давать задачи, которые реально требуют вычислений с вещественными числами — никто, даже само жюри, не может быть уверено в том, что у них eps выбрано верно. Но иногда такие задачи все-таки дают, т.к. никуда не денешься.
Собственно, из этого и следует
В частности, в будущем вы заметите, что во многих задачах, которые, казалось бы, подразумевают вещественные входные данные (например, задачи на геометрию), входные данные тем не менее обычно целочисленны. Это сделано именно для того, чтобы можно было написать решение полностью в целых числах, и не иметь проблем с погрешностью. (Не всегда такое решение возможно, и уж тем более не всегда оно простое, но тем не менее.) Поэтому если вы можете написать такое решение, лучше написать именно его.
Дополнительный материал. «Грубые» задачи: когда eps не нужно
Так иногда бывает — когда вам все равно, в какую ветку if’а вы попадете, если два сравниваемых числа на самом деле равны между собой. В таком случае eps использовать не надо. Но каждый раз тщательно думайте: а правда ли все равно? Всегда лучше перестраховаться и написать eps (выше с eps тоже все работало бы), за исключением совсем уж простых случаев типа приведенного выше вычисления максимума.
Еще пример: считаем сумму положительных элементов массива
Еще пример, где уже eps необходим: определим, какое из двух чисел больше:
Вообще, тут полезно следующее понятие. Назовем задачу (или фрагмент кода) грубым, если ответ на задачу (или результат работы этого фрагмента) меняется не очень сильно (не скачком) при небольшом изменении входных данных, и негрубым в противоположном случае. (Понятие грубости пришло из физики.)
Тогда в задаче (фрагменте кода) eps нужен, если задача является негрубой: тогда существуют такие входные данные, которые вам важно отличить от очень близких им. Например, если надо определить, какое из двух чисел больше, то при входных данных «0.3 0.3» надо ответить «они равны», но при очень небольшом изменении входных данных, например, на «0.300001 0.3» ответ резко меняется: надо отвечать «первое больше».
Если же задача (или фрагмент кода) является грубым, то, скорее всего, в нем можно обойтись без eps : если вы чуть-чуть ошибетесь при вычислениях, ответ тоже изменится не очень сильно. Например, если вы вычисляете максимум из двух чисел, то на входных данных «0.3 0.3» ответ 0.3, а на входных данных «0.300001 0.3» ответ 0.300001, т.е. изменился не очень сильно.
Но, конечно, все приведенное выше рассуждение про грубые задачи — очень примерно, и в каждой задаче надо отдельно думать.
Что такое frac в математике
Смотреть что такое «FRAC» в других словарях:
frac — frac … Dictionnaire des rimes
frac — [ frak ] n. m. • 1767; probablt de l angl. frock, lui même du fr. froc ♦ Habit masculin de cérémonie, noir, à basques en queue de morue. ⇒ habit, 1. queue (queue de pie). ● frac nom masculin (anglais frock, de l ancien français froc) Synonyme… … Encyclopédie Universelle
Frac — Saltar a navegación, búsqueda El frac es un traje masculino de tipo formal que constituye el tipo de vestuario masculino más elegante para la noche, para el día (hasta las 19:00 aproximadamente) se luce chaqué. Sólo el traje nacional tiene la… … Wikipedia Español
frac — FRAC, fracuri, s.n. Haină bărbătească de ceremonie din stofă neagră, în faţă scurtă până la talie, iar în spate terminată cu două cozi lungi şi înguste. – Din fr. frac. Trimis de zaraza joe, 01.04.2008. Sursa: DEX 98 frac s. n., pl. frácuri… … Dicționar Român
Frac — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. En mode, le frac est une variante de la queue de pie En arts, FRAC est un acronyme pour désigner un fonds régional d art contemporain Ce document provient … Wikipédia en Français
frac — s.m.inv. ES fr. <
frac — (plural fraques) sustantivo masculino 1. Chaqueta masculina de etiqueta que por delante llega hasta la cintura y por detrás se prolonga en dos faldones: Era indispensable llevar frac para asistir a la recepción. Con aquel frac parecía un pingüino … Diccionario Salamanca de la Lengua Española
Frac — may refer to:* Fractional part, a mathematical function * In geology, a frac refers to fractures in a rock formation; see Fracture (geology) for natural fractures, or Hydraulic fracture for artificially created fracturesee also* Frak… … Wikipedia
frac — Voz tomada del francés frac, introducida en español a finales del siglo xviii, que designa cierto traje masculino de ceremonia. Muy pronto se puso en circulación la variante fraque, mejor adaptada al español, pero cuyo uso ha sido siempre… … Diccionario panhispánico de dudas
frac — (Del fr. frac). m. Vestidura de hombre, que por delante llega hasta la cintura y por detrás tiene dos faldones más o menos anchos y largos … Diccionario de la lengua española
frac — Mot Monosíl·lab Nom masculí … Diccionari Català-Català
Пошаговые калькуляторы:
Обыкновенные дифференциальные уравнения \(y»=\cos\left(x\right)\)
Калькулятор решает \(F\left(x,\,y,\,y’,\,y»,\dots,y^<\left(n\right)>\right)=0\) — обыкновенные дифференциальные уравнения (ОДУ) разных порядков, а именно:
Уравнения с разделяющимися переменными: \(p\left(x\right)\mathrm
Однородные уравнения: \(y’=f\left(k\,x,\;k\,y\right)=f\left(x,\;y\right)\)
Приведение к однородному подстановкой \(y=z^<\lambda>\)
Линейные уравнения первого порядка: \(y’+a\left(x\right)\,y=b\left(x\right)\)
Дифференциальное уравнение Бернулли: \(y’+a\left(x\right)\,y=b\left(x\right)\,y^n\)
Дифференциальное уравнение Риккати: \(y’+a\left(x\right)\,y+b\left(x\right)\,y^2=c\left(x\right)\)
Уравнение в полных дифференциалах: \(P\left(x,\;y\right)\,\mathrm
Уравнения не разрешенные относительно производной: \(F\left(x,\;y,\;y’\right)=0\) — метод введения параметра \(p\,\) ; вычисление полного дифференциала; замена \(\mathrm
Уравнения, допускающие понижение порядка — замена \(y^<\left(k\right)>=z\) для уравнений вида \(F\left(x,\,y^<\left(k\right)>,\,y^<\left(k+1\right)>,\dots,y^<\left(n\right)>\right)=0\) ; подстановка \(y’=p\left(y\right)\) для \(F\left(y,\,y’,\,y»\,\dots,y^<\left(n\right)>\right)=0\) ; однородное уравнение относительно y и его производных \(y’,\,y»,\dots,y^<\left(n\right)>\) ; однородное относительно \(x\) и \(y\) в обобщенном смысле
Однородные и неоднородные линейные уравнения с постоянными коэффициентами: \(y^<\left(n\right)>+a_
Различные замены из контекста уравнения
Для уравнений первого порядка используется метод Бернулли или вариации произвольной постоянной Лагранжа
Тригонометрические и гиперболические преобразования
Проверка на потерю частных решений
Во время вычислений калькулятор самостоятельно производит группировку, подстановки или домножение уравнения, выбирая в процессе более подходящий метод решения
Неопределенные и определенные интегралы \(\displaystyle\int<\sin^2\left(x\right)><\;\mathrmx>\)
Калькулятор пошагово вычисляет \(\displaystyle \int
Правило интегрирования суммы (разности) \(\displaystyle\int<\left(u\pm v\pm w\right)>\;\mathrm
Вынесение постоянной за знак интеграла \(\displaystyle\int
Интегрирование рациональных функций: тригонометрических \(\mathrm
Произведение степенных функций \(\sin^n\left(x\right)\,\cos^m\left(x\right)\) и гиперболических \(\operatorname
Степенные, логарифмические, тригонометрические и гиперболические преобразования
Подстановки, группировки с использованием упрощений
Для вычисления несобственных интегралов рассматриваются пределы на бесконечности, левосторонние и правосторонние пределы в точках разрыва функции на промежутке
Список задействованных математических функций:
\(\ln\) \(\sin\) \(\cos\) \(\operatorname
Производная функции \(\left(\ln\left(x^2\right)\right)’_x\)
Определены следующие правила:
Матричные вычисления \(\mathrm^<-1>\,\mathrm\)
Калькулятор ориентирован на пошаговое выполнение операций с матрицами \(\mathrm\), \(\mathrm\) и \(\mathrm
Умножение матрицы на константу (любую функцию) \(a\cdot\mathrm\) или сложение с константой \(c+\mathrm\)
Калькулятор обрабатывает как числовые значения, так и комбинации из арифметических операций и функций
Если в ходе решения матрица, либо пара матриц не удовлетворяют условию выполнения текущей операции — отображаются все вычисленные ранее шаги и наглядно указывается несоответствие
При наведении на вычисленные элементы — подсвечиваются все значения, используемые в вычислении. Например, при умножении матриц можно увидеть какие элементы строки и столбца задействованы в расчете
Все не матричные операции проводятся в обычном порядке по ходу вычислений
Как решать интегралы: примеры решения
Обновлено: 12 Октября 2021
Одно из самых значимых понятий в математике — интеграл. Термин часто можно встретить при решении задач по математике и физике. С помощью интеграла существенно упрощается поиск площади под кривой, пройденного пути объекта, движущегося неравномерно, массы неоднородного тела, функции по производной.
Что такое интеграл — понятие и определение
Интеграл представляет собой аналог суммы для бесконечного числа бесконечно малых слагаемых.
Интеграл является эффективным инструментом для решения задач из математического анализа. Слово «интеграл» происходит от латинского «integer», то есть «целый». Впервые это понятие ввел Иоганн Бернулли.
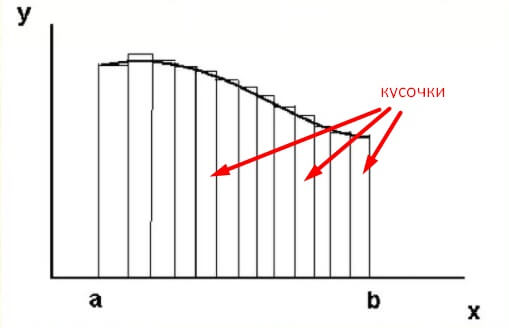
Разобраться в определении интеграла можно, если рассмотреть понятный график функции:
Исходя из графика, можно сделать вывод, что интегралом является сумма малых частей, которые составляют в целом рассматриваемый объект. Компоненты складываются в какую-то геометрическую фигуру. При сложении этих частей можно определить, какова ее площадь. Таким образом, пояснение для интеграла заключается в следующем: интеграл является площадью какой-то фигуры, расположенной под линией функции.
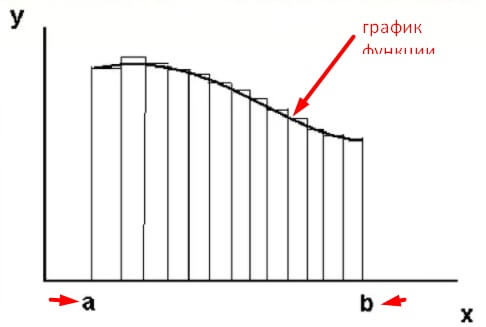
Данное понятие относится к определенному интегралу. Он определен на отрезке между точками а и b. В верхней части в качестве ограничения выступает некоторый график функции, как представлено на рисунке:
Математическая запись интеграла:
где f(x) является той самой функцией, график которой ограничивает фигуру в верхней части;
a и b представляют собой пределы;
x соответствует направлению, вдоль которого построены столбцы на графике.
Процесс интегрирования является обратным дифференцированию. В том случае, когда требуется определить минимальный промежуток заданной функции, целесообразно взять от нее производную. Это объясняется тем, что производная или дифференциал являются быстрым методом поиска части чего-либо. Можно наглядно определить с помощью рисунка, что минимальная фигура, которая является частью целого, при таком числе составляющих компонентов не повторяет форму кривой функции. Таким образом, требуется уменьшить габариты таких частей, чтобы они максимально точно совпадали с графиком. Площадь наименьшего компонента фигуры будет стремиться к нулевому значению. Точность повышается с уменьшением размеров рассматриваемой части. Площадь геометрической фигуры состоит из суммы таких частей, которые стремятся к нулю. Записать это можно с помощью уравнения:
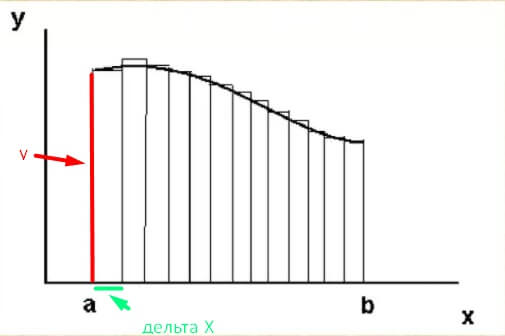
Подробно полученное выражение можно рассмотреть на графике:
Площадь малой части фигуры определяется так же, как площадь прямоугольника. Значение Y нужно помножить на значение ΔХ. Так как фигура представляет собой совокупность малых частей, то их требуется сложить. Следует учитывать, что каждый компонент фигуры ΔХ стремится к нулевому значению. Поэтому формула, которая представлена выше, включает это условие и позволяет определить результат максимально точно.
Если обозначить количество частей ΔХ, стремящихся к бесконечности, то можно определить, что существует предел интегральной суммы, которая состоит из таких компонентов, стремящихся к нулю и к бесконечности по числу таких частей. Таким образом, правая граница фигуры, изображенной на графике, является пределом. В этом выражается геометрический смысл определенного интеграла.
Физический смысл интеграла состоит в том, что это сумма бесконечно малых величин на бесконечно большом интервале. Исходя из этого, можно определить любую величину, которая изменяется, согласно функции. К примеру, рассчитать общий путь по закону изменения скорости. Необходимость в интеграле возникла, когда потребовалось рассчитать площади каких-либо фигур и объем любых тел, выбранных произвольно.
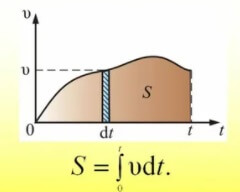
В том случае, когда расчеты подразумевают наличие постоянной характеристики, к примеру, скорости, найти путь можно с помощью произведения этой постоянной скорости и времени. Этот же момент можно проверить при вычислении интеграла от такой функции и записи уравнения прямой. Но скорость в процессе движения может меняться. Данное изменение можно представить в виде зависимости. Тогда следует вписать граничные условия, например, в случае пути — это время, в интеграл скорости по времени. Полученное выражение будет равно площади трапеции, которая расположена под функцией скорости, что является физическим смыслом определенного интеграла.
Свойства, которыми обладает определенный интеграл:
Термин «неопределенный интеграл» применим в ситуациях, когда требует найти площадь криволинейной трапеции, путь в соответствии с известной скоростью тела, которое движется неравномерно, и для решения других подобных задач.
Свойства, которыми характеризуется неопределенный интеграл:
Таблица интегралов для студентов
Такие формулы позволяют упростить решение многих задач. Основные интегралы:
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Найти (с решением) производную функции.
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Немного теории.
Определение производной
Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac<\Delta y> <\Delta x>\). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).
Геометрический смысл производной состоит в следующем. Если к графику функции \( y = f(x) \) в точке с абсциссой \( x=a \) можно провести касательную, непараллельную оси \(y\), то \( f(a) \) выражает угловой коэффициент касательной:
\( k = f'(a) \)
Если функция \(y=f(x)\) имеет производную в точке \(x\), то ее называют дифференцируемой в точке \(x\). Процедуру нахождения производной функции \(y=f(x)\) называют дифференцированием функции \(y=f(x)\).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция \(y=f(x)\) дифференцируема в точке \(x\). Тогда к графику функции в точке \( M(x; \; f(x)) \) можно провести касательную, причем, напомним, угловой коэффициент касательной равен \( f'(x) \). Такой график не может «разрываться» в точке \(M\), т. е. функция обязана быть непрерывной в точке \(x\).
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция \(y=f(x)\) дифференцируема в точке \(x\), то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция \( y=|x|\) непрерывна везде, в частности в точке \(x=0\), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция \( y=\sqrt[3]
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если \(C\) — постоянное число и \( f=f(x), \; g=g(x) \) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: