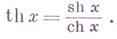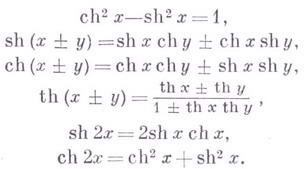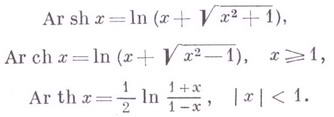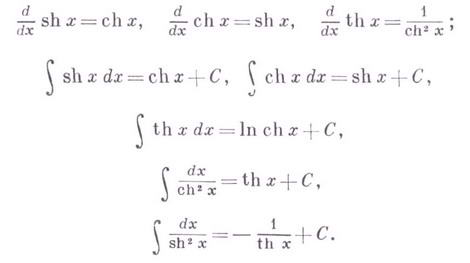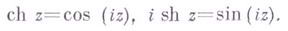ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

функции, определяемые формулами:

— гиперболический синус,

-г иперболический косинус.

Иногда рассматривается также гиперболический тангенс;

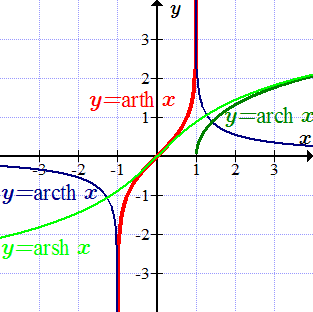
Другие обозначения: sinh x,Sh x,cosh x, Ch x,tgh x,tanh x,Th x. Графики см. на рис. 1.

Производные и основные интегралы от Г. ф.:

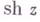
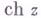
Во всей плоскости комплексного переменного z Г. ф. и могут быть определены рядами:

Полезное

Смотреть что такое «ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ» в других словарях:

Гиперболические функции — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус). Иногда рассматривается также гиперболический тангенс: (графики Г. ф. см. на рис. 1). Г. ф.… … Большая советская энциклопедия

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус), (гиперболический тангенс) … Большой Энциклопедический словарь

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: shx = (ex e x)/2(гинерболич. синус), chх (еx + е к)/2 (гиперболич. косинус), thх = shx/chx (гиперболич. тангенс). Графики Г. ф. см. на рис … Естествознание. Энциклопедический словарь

Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия

гиперболические функции — функции, определяемые формулами: shx = (ex – e x)/2 (гиперболический синус), chx = (ex + e x)/2 (гиперболический косинус), thx = shx/chx (гиперболический тангенс). Графики гиперболических функций см. на рис. * * * ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ… … Энциклопедический словарь

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Функции. определяемые ф лами: (гиперболич. синус), (гиперболич. косинус), (вставить рисунки. ) Графики гиперболических функций … Большой энциклопедический политехнический словарь

Гиперболические функции — По аналогии с тригонометрическими функциями Sinx, cosx, определяемыми, как известно, при помощи Эйлеровых формул sinx = (exi e xi)/2i, cosx = (exi + e xi)/2 (где е есть основание нэперовых логарифмов, a i = √[ 1]); иногда вводятся в рассмотрение… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Обратные гиперболические функции — функции, обратные по отношению к гиперболическим функциям (См. Гиперболические функции) sh х, ch х, th х; они выражаются формулами (читается: ареа синус гиперболический, ареа косинус гиперболический, ареа тангенс… … Большая советская энциклопедия

ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, обратные к гиперболич. функциям; выражаются формулами … Естествознание. Энциклопедический словарь

Обратные гиперболические функции — Обратные гиперболические функции определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… … Википедия

Источник

Гиперболические функции

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Содержание

Определение

Определение гиперболических функций через гиперболу

Один из способов определения тригонометрических функций через единичную окружность

Гиперболические функции задаются следующими формулами:

Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.

Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.

Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно.

Иногда также определяются

Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно.

Геометрическое определение

Ввиду соотношения гиперболические функции дают параметрическое представление гиперболы (, ). При этом аргумент , где — площадь криволинейного треугольника , взятая со знаком «+», если сектор лежит выше оси , и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Свойства

Связь с тригонометрическими функциями

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

.

Важные тождества

Разложение в степенные ряды

Здесь — числа Бернулли.

Графики

Аналитические свойства

Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках , где — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек , вычеты его в этих полюсах также равны единице.

Обратные гиперболические функции

Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».

— обратный гиперболический синус: — обратный гиперболический косинус — обратный гиперболический тангенс — обратный гиперболический котангенс — обратный гиперболический секанс 0\end>\right.>» /> — обратный гиперболический косеканс

Эти функции имеют следующее разложение в ряд:

1>» />

История

Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы.

Применение

Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.

Ссылки

cs:Hyperbolická funkce he:פונקציות היפרבוליות hu:Hiperbolikus függvények is:Breiðbogafall nl:Hyperbolische functie pl:Funkcje hiperboliczne sr:Хиперболичне функције sv:Hyperbolisk funktion

Источник

Что такое chx в математике

Гиперболические синус (shx) и косинус (chx) можно определить следующим образом:

Гиперболические тангенс (thx), котангенс (cthx), секанс (sechx) и косеканс (cosechx) можно задать аналогично соответствующим тригонометрическим функциям:

Отсюда получаются следующие формулы:

Свойства гиперболических функций во многом аналогичны свойствам тригонометрических функций.

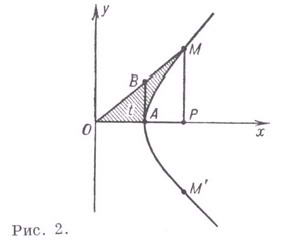
Подобно тому как тригонометрические функции синус и косинус параметрически определяют тригонометрическую окружность х 2 + у 2 = 1 уравнениями х = cost, y = sint, уравнения x = cht, y = sht – параметрические уравнения равнобочной гиперболы x 2 – y 2 = 1.

Из определений легко следует нечетность гиперболических синуса, тангенса, котангенса и косеканса, а также четность гиперболических косинуса и секанса.

Для гиперболических функций, как и для тригонометрических, имеют место теоремы сложения:

Как обычно, положив в этих формулах у = х, приходим к формулам удвоения аргумента:

Источник

Учебник. Гиперболические функции

Подобно тому, как тригонометрические синус и косинус являются координатами точки на координатной окружности, гиперболические синус и косинус являются координатами точки на гиперболе.

Графики функций y = sh x и y = ch x

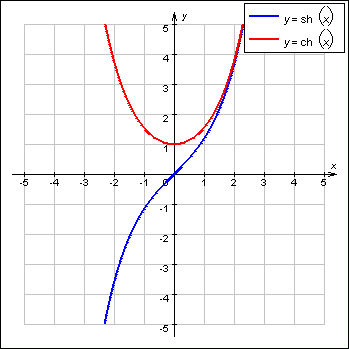
Тангенс определён на всей числовой оси, котангенс – при всех x ≠ 0 ( lim x → ± 0 cth x = ± ∞ ). Обе функции непрерывны на всей области определения, нечетны и имеют горизонтальные ( и (

Графики функций y = th x и y = сth x

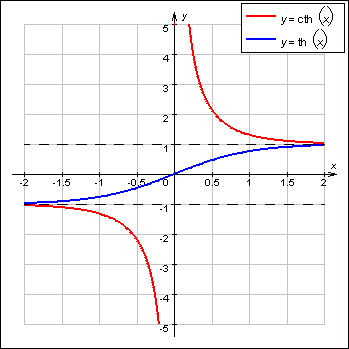
Приведём некоторые формулы, связанные с гиперболическими функциями.

sh x + ch x = e x
ch 2 x – sh 2 x = 1 ch 2x = ch 2 x + sh 2 x sh 2x = 2 sh x ch x sh (x + y) = sh x ch y + ch x sh y ch (x + y) = ch x ch y + sh x sh y

Функции, обратные гиперболическим синусу и тангенсу, определены и непрерывны на всей числовой оси. Они обозначаются соответственно arsh x и arth x. У гиперболического косинуса определены сразу две обратные функции: arch_– x при x ≤ 0 и arch₊ x при x ≥ 0.

Графики функций y = arsh x и y = arth x. Графики функции y = arch_– x и y = arch₊ x.

Источник

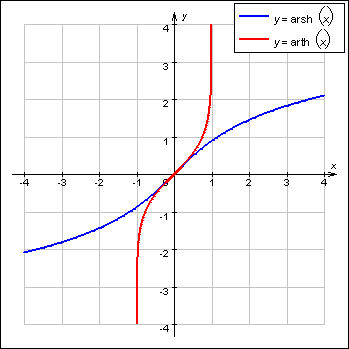
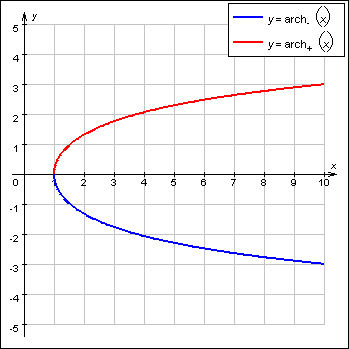
Обратные гиперболические функции, их графики и формулы

Определения обратных гиперболических функций, их области определений и значений

Ареасинус строго возрастает на всей числовой оси.

Ареакосинус строго возрастает на своей области определения.

Вторая ветвь ареакосинуса также определена при x ≥ 1 и расположена симметрично относительно оси абсцисс, – ∞ 0 :
. Она строго убывает на области определения.

Ареатангенс строго возрастает на своей области определения.

Ареакотангенс строго убывает на своей области определения.

Графики обратных гиперболических функций

Формулы с обратными гиперболическими функциями

Связь с тригонометрическими функциями

Четность

Формулы связи обратных гиперболических синусов через тангенсы и косинусов через котангенсы

Формулы суммы и разности

Производные обратных гиперболических функций

Интегралы от arsh x, arch x, arth x, arcth x

arsh x

Для вычисления интеграла от гиперболического арксинуса, делаем подстановку x = sh t и интегрируем по частям:
.

arch x

Аналогично, для гиперболического арккосинуса. Делаем подстановку x = ch t и интегрируем по частям учитывая, что t ≥ 0 :
.

arth x

arcth x

Разложения в ряды

arsh x

При |x| 1 имеет место следующее разложение:

arth x

При |x| 1 имеет место следующее разложение:

arcth x

При |x| > 1 имеет место следующее разложение:

Обратные функции

Гиперболический синус

При – ∞ и – ∞ имеют место формулы:
,
.

Гиперболический косинус

При 1 ≤ y и 0 ≤ x имеют место формулы:
,
.

Гиперболический тангенс

При – 1 1 и – ∞ имеют место формулы:
,
.

Гиперболический котангенс

При – ∞ 1 или 1 и x ≠ 0 имеют место формулы:
,
.

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Источник