Что такое cdf в статистике

Кумулятивная функция распределения в нормально распределенных данных

В данной статье объясняется, как получить кумулятивную функцию распределения Гаусса и почему она полезна в статистическом анализе.

Если вы только присоединяетесь к нашему обсуждению статистики в электротехнике, возможно, вам будет интересно сначала просмотреть предыдущие статьи этой серии, список которых можно найти в оглавлении вверху над статьей.

Что мы знаем из предыдущих статей:

Если участки интегрирования функции плотности вероятности являются ключом к извлечению вероятностей из измеренных данных, можно задаться вопросом о возможности простого интегрирования всей функции и тем самым создания новой функции, которая даст нам прямой доступ к информации о вероятности.

Как оказалось, это стандартный метод статистического анализа, и эта новая функция, которую мы получаем путем интегрирования всей функции плотности вероятности, называется кумулятивной функцией распределения.

Кумулятивная функция нормального распределения

Использование кумулятивной функции распределения (CDF, cumulative distribution function) является особенно хорошей идеей, когда мы работаем с нормально распределенными данными, потому что интегрировать гауссову кривую не так-то просто.

Фактически, чтобы получить кумулятивную функцию распределения кривой Гаусса, даже математики должны прибегнуть к численному интегрированию (функция \(e^<-x^2>\) не имеет первообразной, которая может быть выражена в элементарной форме). Это означает, что кумулятивная функция распределения Гаусса на самом деле представляет собой последовательность дискретных значений, созданных из множества отдельных выборок, взятых вдоль гауссовой кривой.

В эпоху компьютеров мы можем легко обрабатывать огромное количество выборок, и, следовательно, дискретная кумулятивная функция распределения, полученная путем численного интегрирования, может быть вполне адекватной заменой непрерывной функции, полученной посредством символьного интегрирования.

Если мы отложим на графике большое количество значений гауссовой функции распределения, кривая будет выглядеть следующим образом:

Рисунок 1 – Кумулятивная функция нормального распределения

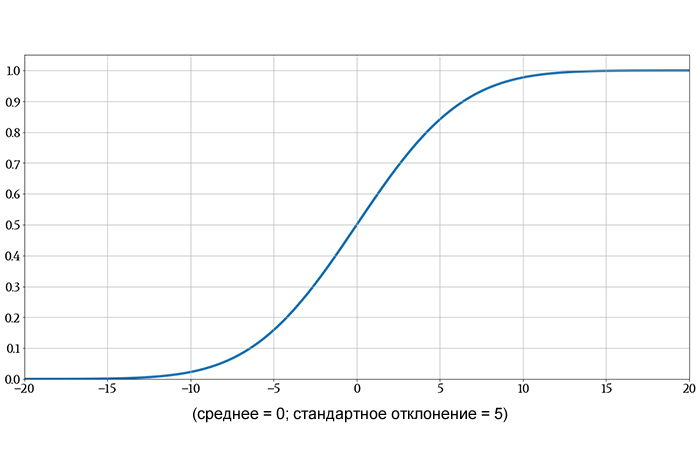
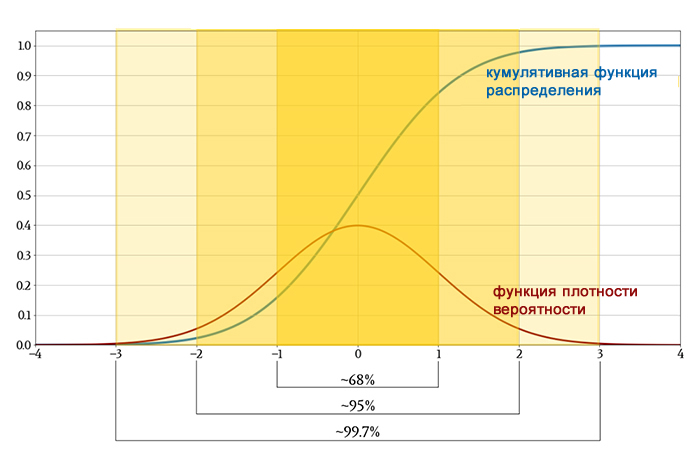
На следующем графике показаны как исходная гауссова функция плотности вероятности, так и ее функция распределения, чтобы вы могли увидеть, как интегрирование превращает одно в другое.

Рисунок 2 – Функция плотности вероятности нормально распределенной переменной и соответствующая функция распределения

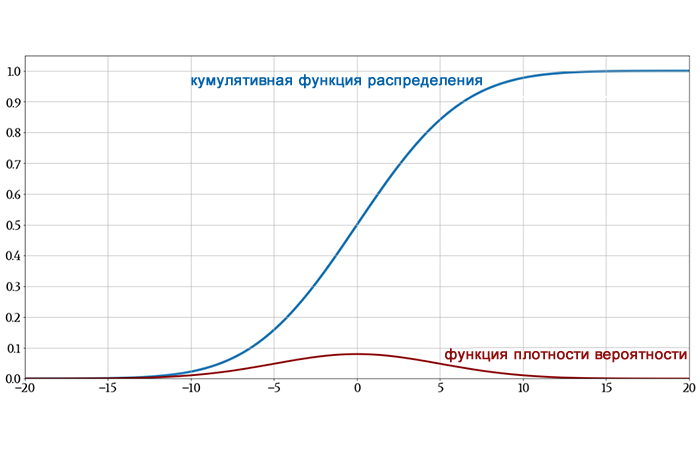
Одно небольшое замечание, прежде чем мы продолжим: в обсуждениях о статистике вы можете увидеть символ Φ (заглавная греческая буква фи). Когда нормальное распределение имеет среднее значение 0 и стандартное отклонение 1, оно называется стандартным нормальным распределением. Кумулятивная функция стандартного нормального распределения обозначается Φ; таким образом,

Пример кумулятивной функции распределения

Когда мы интегрируем функцию плотности вероятности от отрицательной бесконечности до некоторого значения, обозначенного z, мы вычисляем вероятность того, что результат случайно выбранного измерения или нового измерения попадет в числовой интервал, который простирается от отрицательной бесконечности до z. Другими словами, мы вычисляем вероятность того, что измеренное значение будет меньше z.

Это именно та информация, которую мы получаем из кумулятивной функции распределения и без необходимости интегрирования. Если мы посмотрим на график кумулятивной функции распределения и найдем вертикальное значение, соответствующее некоторому числу z на горизонтальной оси, мы узнаем вероятность того, что измеренное значение будет меньше z.

Рисунок 3 – Определение вероятности того, что измеренное значение будет меньше некоторой величины, с помощью кумулятивной функции распределения

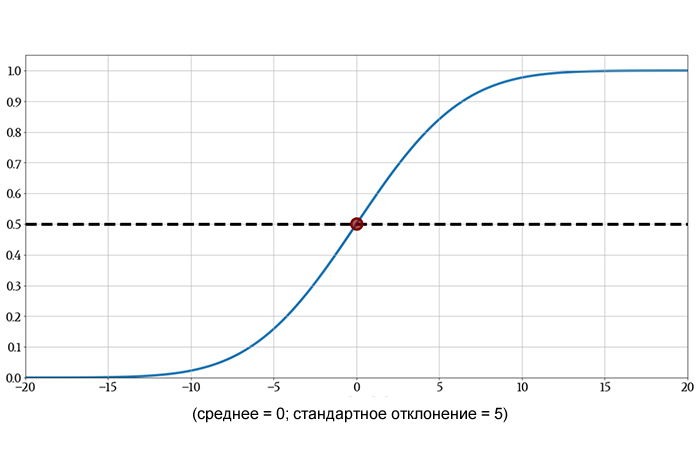
Кумулятивная функция распределения при z = 0 равна 0,5. Это говорит нам о том, что результат выбранного случайным образом измерения имеет 50% вероятность быть меньше нуля. Это интуитивно понятно: нормальное распределение симметрично относительно среднего, и поскольку среднее значение в этом случае равно нулю, любое отдельное измерение имеет равные шансы быть меньше или больше нуля.

Кумулятивная функция распределения (CDF) также обеспечивает простой способ определения вероятности того, что результат измерения попадет в определенный диапазон. Если диапазон определяется двумя значениями z₁ и z₂, всё, что нам нужно сделать, это вычесть значение функции распределения в z₂ из значения функции распределения в z₁ (а затем при необходимости взять модуль полученного значения).

Вот еще один пример:

Рисунок 4 – Определение вероятности попадания результата измерения в определенный диапазон с помощью кумулятивной функции распределения

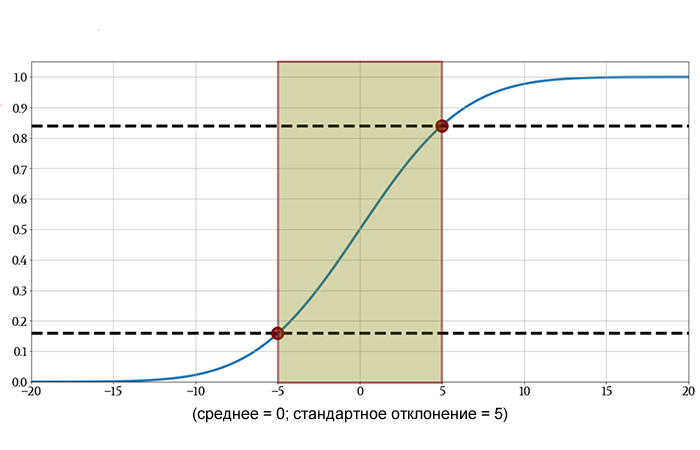
Вероятность того, что результат случайно выбранного измерения будет между –5 и +5, составляет приблизительно (0,84 – 0,16) = 0,68 (или 68%). Более точное значение – 68,27%.

Вероятность и стандартное отклонение

Вы могли заметить, что интервал, выбранный в предыдущем примере, был равен одному стандартному отклонению выше и ниже среднего. Когда мы обсуждаем вероятности со ссылкой на интервалы, представленные в единицах стандартного отклонения, эта информация применяется ко всем наборам данных, которые следуют нормальному распределению. Таким образом, мы можем определить вероятностные характеристики, используя кумулятивную функцию стандартного нормального распределения, а затем распространить эти тенденции на другие наборы данных, просто изменив стандартное отклонение (или размышляя относительно стандартных отклонений).

Выше мы видели, что в нормально распределенных данных измеренное значение имеет шанс 68,27% попасть в диапазон в пределах одного стандартного отклонения от среднего. Мы можем продолжить обобщение нормально распределенных данных следующим образом:

Эти три вероятности дают простое представление того, как будут вести себя нормально распределенные измерения.

Более приблизительная версия этого обобщения известна как правило 68-95-99,7: если набор данных демонстрирует нормальное распределение, около 68% значений будут в пределах одного стандартного отклонения от среднего, около 95% будут в пределах двух стандартных отклонений, и около 99,7% будут в пределах трех стандартных отклонений.

Рисунок 5 – Демонстрация правила 68-95-99,7 на графиках функции плотности вероятности и функции распределения

Заключение

Мы рассмотрели важный материал, и я надеюсь, что вам понравилось наше исследование нормального распределения и связанных с ним тем статистики. В следующей статье мы рассмотрим два малоизвестных описательных статистических показателя: асимметрию и эксцесс.

Источник

Python, исследование данных и выборы: часть 3

Пост №3 для начинающих посвящен генерированию распределений, их свойствам, а также графикам для их сопоставительного анализа. Предыдущий пост см. здесь.

Булочник и Пуанкаре

Существует легенда, почти наверняка апокрифическая, которая дает возможность детальнее рассмотреть вопрос о том, каким образом центральная предельная теорема позволяет рассуждать о принципе формирования статистических распределений. Она касается прославленного французского эрудита XIX-ого века Анри Пуанкаре, который, как гласит легенда, в течение одного года каждый день занимался тем, что взвешивал свежую буханку хлеба.

В те времена хлебопекарное ремесло регламентировалось государством, и Пуанкаре обнаружил, что, хотя результаты взвешивания буханок хлеба подчинялись нормальному распределению, пик находился не на публично афишируемом 1 кг, а на 950 г. Он сообщил властям о булочнике, у которого он регулярно покупал хлеб, и тот был оштрафован. Такова легенда ;-).

В следующем году Пуанкаре продолжил взвешивать буханки хлеба того же булочника. Он обнаружил, что среднее значение теперь было равно 1 кг, но это распределение больше не было симметричным вокруг среднего значения. Теперь оно было смещено вправо. А это соответствовало тому, что булочник теперь давал Пуанкаре только самые тяжелые из своих буханок хлеба. Пуанкаре снова сообщил о булочнике властям, и булочник был оштрафован во второй раз.

Было ли это на самом деле или нет здесь не суть важно; этот пример всего лишь служит для того, чтобы проиллюстрировать ключевой момент — статистическое распределение последовательности чисел может сообщить нам нечто важное о процессе, который ее создал.

Генерирование распределений

В целях развития нашего интуитивного понимания относительно нормального распределения и дисперсии, давайте смоделируем честного и нечестного булочников, и для этого воспользуемся функцией генерирования нормально распределенных случайных величин stats.norm.rvs. (rvs от англ. normal variates, т.е. нормально-распределенные случайные величины). Честного булочника можно смоделировать в виде нормального распределения со средним значением 1000, что соответствует справедливой буханке хлеба весом 1 кг. При этом мы допустим наличие дисперсии в процессе выпекания, которая приводит к стандартному отклонению в 30г.

Приведенный выше пример построит гистограмму, аналогичную следующей:

Теперь смоделируем булочника, который продает только самые тяжелые буханки хлеба. Мы разобьем последовательность на группы по тринадцать элементов (на «чертовы дюжины») и отберем максимальное значение в каждой:

Приведенный выше пример создаст гистограмму, аналогичную следующей:

Совершенно очевидно, что эта гистограмма выглядит не совсем так, как другие, которые мы видели. Среднее значение по-прежнему равно 1 кг, но разброс значений вокруг среднего больше не является симметричным. Мы говорим, что эта гистограмма показывает смещенное нормальное распределение.

Асимметрия

Асимметрией называется смещение распределения относительно ее моды. Отрицательная асимметрия, или левое смещение кривой, указывает на то, что площадь под графиком больше на левой стороне моды. Положительная асимметрия, или правое смещение кривой, указывает на то, что площадь под графиком больше на правой стороне моды.

Положительная и отрицательная асимметрии

Библиотека pandas располагает функцией skew для измерения асимметрии:

Приведенный выше пример показывает, что коэффициент асимметрии в выпечке от нечестного булочника составляет порядка 0.4. Этот коэффициент количественно определяет степень скошенности, которая видна на гистограмме.

Графики нормального распределения

Ранее в этой серии постов мы познакомились с квантилями как средством описания статистического распределения данных. Напомним, что функция quantile принимает число между 0 и 1 и возвращает значение последовательности в этой точке. 0.5-квантиль соответствует значению медианы.

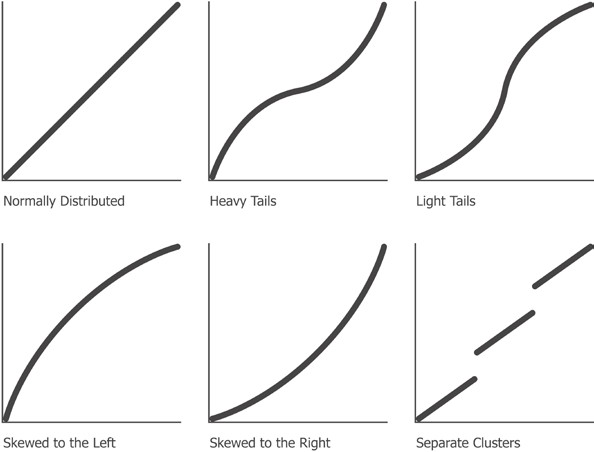
Изображение квантилей данных относительно квантилей нормального распределения позволяет увидеть, каким образом наши измеренные данные соотносятся с теоретическим распределением. Подобные графики называются квантильными графиками, или диаграммами квантиль-квантиль, графиками Q-Q, от англ. Q-Q plot. Они предоставляют быстрый и интуитивно понятный способ определить степень нормальности статистического распределения. Для данных, которые близки к нормальному распределению, квантильный график покажет прямую линию. Отклонения от прямой линии показывают, каким образом данные отклоняются от идеализированного нормального распределения.

Теперь построим квантильные графики для честного и нечестного булочников. Функция qqplot принимает список точек данных и формирует график выборочных квантилей, отображаемых относительно квантилей из теоретического нормального распределения:

Приведенный выше пример создаст следующие ниже графики:

Выше показан квантильный график для честного булочника. Далее идет квантильный график для нечестного булочника:

Тот факт, что линия имеет изогнутую форму, показывает, что данные положительно асимметричны; наклон в другую сторону будет означать отрицательную асимметрию. Квантильный график в сущности позволяет легко различить целый ряд отклонений от стандартного нормального распределения, как показано на следующем ниже рисунке:

Надписи: нормально распределенные, тяжелые хвосты, легкие хвосты, скошенность влево, скошенность вправо, раздельные кластеры

Квантильные графики сопоставляют статистическое распределение честного и нечестного булочника с теоретическим нормальным распределением. В следующем разделе мы сравним несколько альтернативных способов визуального сопоставления двух (или более) измеренных последовательностей значений.

Технические приемы сопоставительной визуализации

Квантильные графики дают замечательную возможность сопоставить измеренное эмпирическое (выборочное) распределение с теоретическим нормальным распределением. Однако если мы хотим сопоставить друг другу два или более эмпирических распределения, то графики нормального распределения для этого не подойдут. Впрочем, у нас есть несколько других вариантов, как показано в следующих двух разделах.

Коробчатые диаграммы

Коробчатые диаграммы, или диаграммы типа «ящик с усами», — это способ визуализации таких описательных статистик, как медиана и дисперсия. Мы можем сгенерировать их с помощью следующего исходного кода:

Этот пример создаст следующую диаграмму:

Ящики в центре диаграммы представляют интерквартильный размах. Линия поперек ящика — это медиана. Большая точка — это среднее. Для честного булочника линия медианы проходит через центр окружности, показывая, что среднее и медиана примерно одинаковые. Для нечестного булочника среднее отодвинуто от медианы, что указывает на смещение.

Усы показывают на диапазон данных. Выбросы представлены полыми кругами. Всего одна диаграмма позволяет яснее увидеть расхождение между двумя статистическими распределениями, чем рассматривать их отдельно на гистограмме или квантильном графике.

Интегральные функции распределения

Интегральные функции распределения (ИФР), также именуемые кумулятивными функциями распределения, от англ. Cumulative Distribution Function (CDF), описывают вероятность, что значение, взятое из распределения, будет меньше x. Как и все распределения вероятностей, их значения лежат в диапазоне между 0 и 1, где 0 — это невозможность, а 1 — полная определенность. Например, представьте, что я собираюсь бросить шестигранный кубик. Какова вероятность, что выпадет значение меньше 6?

Для уравновешенного кубика вероятность выпадения пятерки или меньшего значения равна 5/6. И наоборот, вероятность, что выпадет единица, равна всего 1/6. Тройка или меньше соответствуют равным шансам — то есть вероятности 50%.

ИФР выпадения чисел на кубике следует той же схеме, что и все ИФР — для чисел на нижнем краю диапазона ИФР близка к нулю, что соответствует низкой вероятности выбора чисел в этом диапазоне или ниже. На верхнем краю диапазона ИФР близка к единице, поскольку большинство значений, взятых из последовательности, будет ниже.

ИФР и квантили тесно друг с другом связаны — ИФР является инверсией квантильной функции. Если 0.5-квантиль соответствует значению 1000, тогда ИФР для 1000 составляет 0.5.

Подобно тому, как функция pandas quantile позволяет нам отбирать значения из распределения в конкретных точках, эмпирическая ИФР empirical_cdf позволяет нам внести значение из последовательности и вернуть значение в диапазоне между 0 и 1. Это функция более высокого порядка, т.е. она принимает значение (в данном случае последовательность значений) и возвращает функцию, которую потом можно вызывать, сколько угодно, с различными значениями на входе, и возвращая ИФР для каждого из них.

Функции более высокого порядка — это функции, которые принимают или возвращают функции.

Приведенный выше пример сгенерирует следующий график:

Несмотря на то, что этот график выглядит совсем по-другому, он в сущности показывает ту же самую информацию, что и коробчатая диаграмма. Мы видим, что две линии пересекаются примерно в медиане 0.5, соответствующей 1000 гр. Линия нечестного булочника обрезается в нижнем хвосте и удлиняется на верхнем хвосте, что соответствует асимметричному распределению.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Следующая часть, часть 4, серии постов «Python, исследование данных и выборы» посвящена техническим приемам визуализации данных.

Источник

Нежное введение в распределение статистических данных

Дата публикации 2018-06-08

Выборка данных будет формировать распределение, и на сегодняшний день наиболее известным распределением является распределение Гаусса, которое часто называют нормальным распределением.

Распределение предоставляет параметризованную математическую функцию, которую можно использовать для расчета вероятности любого отдельного наблюдения из выборочного пространства. Это распределение описывает группировку или плотность наблюдений, называемую функцией плотности вероятности. Мы также можем рассчитать вероятность того, что наблюдение будет иметь значение, равное или меньшее заданного значения. Краткое изложение этих взаимосвязей между наблюдениями называется функцией кумулятивной плотности.

В этом руководстве вы узнаете о гауссовских и связанных с ними функциях распределения и о том, как рассчитать вероятности и функции кумулятивной плотности для каждой из них.

После завершения этого урока вы узнаете:

Обзор учебника

Этот урок разделен на 4 части; они есть:

Распределения

С практической точки зрения, мы можем думать о распределении как о функции, которая описывает связь между наблюдениями в пространстве выборки.

Многие данные соответствуют хорошо известным и понятным математическим функциям, таким как распределение Гаусса. Функция может соответствовать данным с модификацией параметров функции, таких как среднее значение и стандартное отклонение в случае гауссиана.

Как только функция распределения известна, ее можно использовать в качестве краткого описания для описания и вычисления связанных величин, таких как вероятности наблюдений, и построения графика отношений между наблюдениями в домене.

Функции плотности

Распределения часто описываются в терминах их плотности или функций плотности.

Функция плотности вероятности, или PDF, может использоваться для вычисления вероятности данного наблюдения в распределении. Его также можно использовать для обобщения вероятности наблюдений в пространстве выборки распределения. Графики PDF показывают знакомую форму распределения, такую ​​как кривая колокола для распределения Гаусса.

Распределения часто определяются в терминах их функций плотности вероятности с соответствующими параметрами.

И PDF-файлы, и CDF-файлы являются непрерывными функциями. Эквивалент PDF для дискретного распределения называется функцией вероятности или PMF.

Далее, давайте посмотрим на распределение Гаусса и два других распределения, связанных с гауссовым распределением, с которыми вы столкнетесь при использовании статистических методов. Мы рассмотрим каждый из них с точки зрения их параметров, вероятности и кумулятивных функций плотности.

Гауссово Распределение

Гауссовское распределение, названное в честь Карла Фридриха Гаусса, находится в центре внимания многих областей статистики.

Данные из многих областей исследования неожиданно могут быть описаны с использованием распределения Гаусса, настолько, что распределение часто называют «нормальныйРаспределение, потому что это так часто

Гауссово распределение может быть описано с использованием двух параметров:

Обычно используется нормализованный расчет дисперсии, называемый стандартным отклонением.

Мы можем работать с гауссовым распределением черезнорм SciPy модуль, Функция norm.pdf () может использоваться для создания гауссовой функции плотности вероятности с заданным пространством выборки, средним значением и стандартным отклонением.

Выполнение примера создает линейный график, показывающий выборочное пространство по оси X и вероятность каждого значения по оси Y. Линейный график показывает знакомую форму колокола для распределения Гаусса.

В верхней части колокольчика показано наиболее вероятное значение из распределения, называемое ожидаемым значением или средним значением, которое в этом случае равно нулю, как мы указали при создании распределения.

Функция norm.cdf () может быть использована для создания гауссовой функции кумулятивной плотности.

В приведенном ниже примере создается гауссовский CDF для того же образца пространства.

При выполнении примера создается график, показывающий S-образную форму с пробным пространством на оси X и совокупной вероятностью на оси Y.

Мы можем видеть, что значение 2 охватывает почти 100% наблюдений с очень тонким хвостом распределения за этой точкой.

Мы также можем видеть, что среднее значение нуля показывает 50% наблюдений до и после этой точки.

Студенческий T-Distribution

T-дистрибутив Студента, или просто t-дистрибутив, для псевдонима «Студент» назван Уильямом Сили Госсетом.

Это распределение, которое возникает при попытке оценить среднее нормального распределения с выборками разных размеров. Таким образом, это полезное сокращение при описании неопределенности или ошибки, связанной с оценкой статистики населения для данных, полученных из гауссовых распределений, когда размер выборки должен быть принят во внимание.

Хотя вы не можете напрямую использовать t-распределение Стьюдента, вы можете оценивать значения по распределению, требуемому в качестве параметров других статистических методов, таких как тесты статистической значимости.

Распределение может быть описано с использованием одного параметра:

Ключом к использованию t-распределения является знание желаемого количества степеней свободы.

Число степеней свободы описывает количество единиц информации, используемых для описания количества населения. Например, среднее имеетNстепени свободы как всеNнаблюдения в выборке используются для расчета оценки среднего населения. Статистическая величина, которая использует другую статистическую величину в своем расчете, должна вычесть 1 из степеней свободы, таких как использование среднего значения в расчете дисперсии выборки.

Наблюдения в t-распределении Стьюдента рассчитываются на основе наблюдений в нормальном распределении, чтобы описать интервал для среднего числа населения в нормальном распределении. Наблюдения рассчитываются как:

Какой конкретный дистрибутив вы используете для данной проблемы, зависит от размера вашей выборки.

SciPy предоставляет инструменты для работы с t-дистрибутивом вмодуль stats.t,t.pdf ()Функция может быть использована для создания t-распределения Стьюдента с указанными степенями свободы.

Выполнение примера создает и строит график t-дистрибутива PDF.

Мы можем видеть знакомую форму колокольчика в распределении, очень похожем на нормальное Ключевым отличием являются более толстые хвосты в распределении, что подчеркивает повышенную вероятность наблюдений в хвостах по сравнению с гауссовой.

t.cdf ()Функция может быть использована для создания кумулятивной функции плотности для t-распределения. Пример ниже создает CDF в том же диапазоне, что и выше.

При выполнении примера мы видим знакомую S-образную кривую, как мы видим с гауссовым распределением, хотя с более мягкими переходами от нулевой вероятности к одной вероятности для более толстых хвостов.

Распределение хи-квадрат

Распределение хи-квадрат обозначается как строчная греческая буква чи (X), возведенная во вторую степень (X ^ 2).

Как и t-распределение Стьюдента, распределение хи-квадрат также используется в статистических методах данных, полученных из гауссовского распределения, для количественной оценки неопределенности. Например, распределение хи-квадрат используется в статистических тестах хи-квадрат на независимость. Фактически, распределение хи-квадрат используется при выводе t-распределения Стьюдента.

Распределение хи-квадрат имеет один параметр:

Наблюдение в распределении хи-квадрат рассчитывается как суммаКквадрат наблюдения, полученные из гауссовского распределения.

кудачиэто наблюдение, которое имеет распределение хи-квадрат,Икснаблюдения взяты из гауссовского распределения, иКэто числоИкснаблюдений, который также является числом степеней свободы для распределения хи-квадрат.

Опять же, как и в случае t-распределения Стьюдента, данные не соответствуют распределению хи-квадрат; вместо этого из этого распределения взяты наблюдения при расчете статистических методов для выборки гауссовских данных.

SciPy предоставляетмодуль stats.chi2для расчета статистики для хи-квадрат распределения. Функция chi2.pdf () может использоваться для вычисления распределения хи-квадрат для выборочного пространства между 0 и 50 с 20 степенями свободы. Напомним, что значения в квадрате суммы должны быть положительными, отсюда и необходимость в положительном выборочном пространстве.

При выполнении примера вычисляется PDF-файл в хи-квадрат и представляется в виде линейного графика.

Хотя распределение имеет колоколообразную форму, распределение не является симметричным.

Функция chi2.cdf () может быть использована для вычисления кумулятивной функции плотности в том же пространстве выборки.

Выполнение примера создает график функции кумулятивной плотности для распределения хи-квадрат.

Распределение помогает увидеть вероятность значения хи-квадрат около 20 с жирным хвостом справа от распределения, которое будет продолжаться еще долго после окончания графика.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

статьи

Резюме

В этом уроке вы обнаружили гауссовы и связанные с ними функции распределения, а также способы вычисления вероятности и функции кумулятивной плотности для каждой из них.

В частности, вы узнали:

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Источник