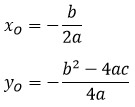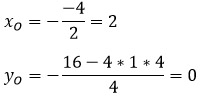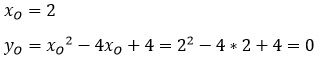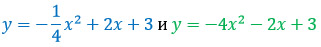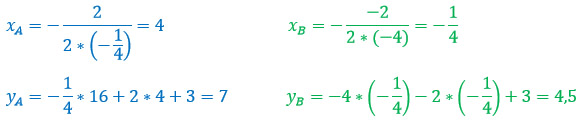Что такое b в функции ax2 bx c
Как определить a, b и c по графику параболы
Предположим, вам попался график функции \(y=ax^2+bx+c\) и нужно по этому графику определить коэффициенты \(a\), \(b\) и \(c\). В этой статье я расскажу 3 простых способа сделать это.
1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью \(y\) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент \(a\) можно найти с помощью следующих фактов:
— Если \(a>0\), то ветви параболы направленных вверх, если \(a 1\), то график вытянут вверх в \(a\) раз по сравнению с «базовым» графиком (у которого \(a=1\)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: \(y=ax^2+bx+c\). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим \(9a\) вместо \(b\):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки \(A\) и \(B\) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение \(a\):
Получается квадратичная функция: \(y=-x^2-9x-15\).
Сразу заметим, что по графику можно сразу определить, что \(c=4\). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: \(C(-1;8)\), \(D(1;2)\) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Сам способ базируется на следующих идеях:
График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).
– Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
— График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц.
График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).
То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:
Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).
Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).
Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
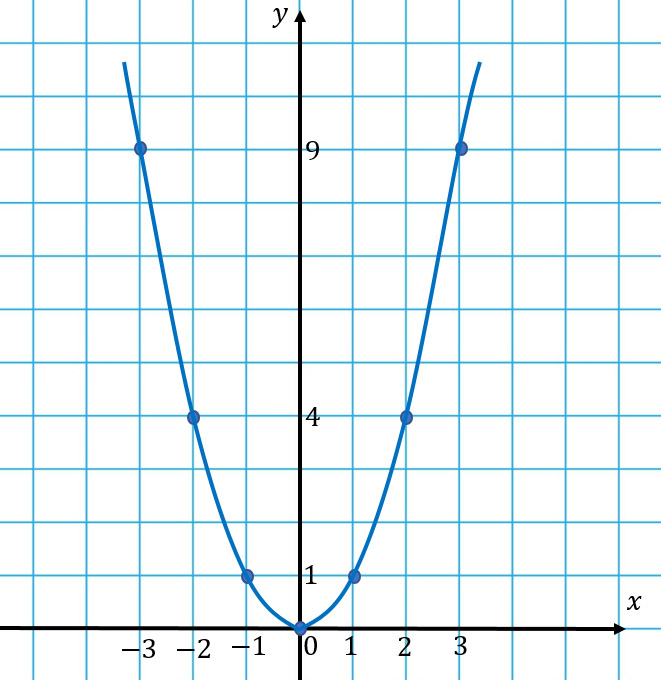
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
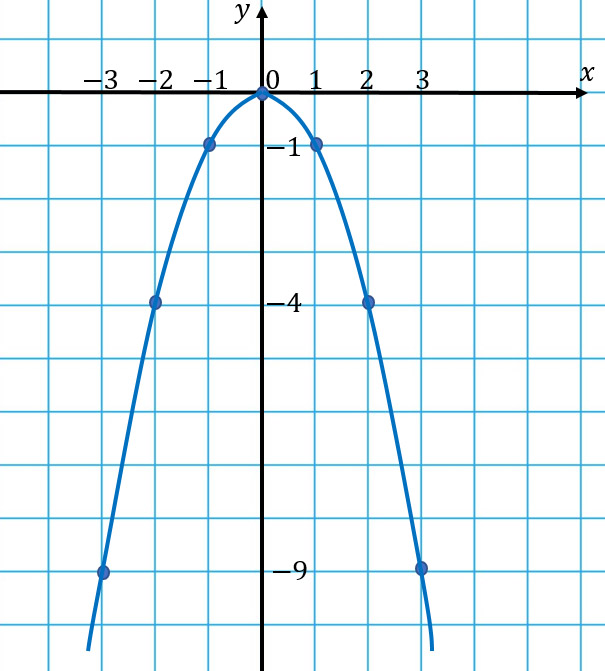
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Квадратичная функция. Парабола
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Квадратичная функция — это функция вида
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
Как построить график квадратичной функции
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции « y = x 2 −7x + 10 ».
Если « a > 0 », то ветви направлены вверх.
Если « a », то ветви направлены вниз.
В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.
Чтобы найти « x0 » (координата вершины по оси « Ox ») нужно использовать формулу:
Найдем « x0 » для нашей функции « y = x 2 −7x + 10 ».
Теперь нам нужно найти « y0 » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x0 » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».
Для начала давайте разберемся, что называют нулями функции.
Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».
0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x1;2 =
| 7 ± √ 49 − 4 · 1 · 10 |
| 2 · 1 |
x1;2 =
| 7 ± √ 9 |
| 2 |
x1;2 =
| 7 ± 3 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 5 | x2 = 2 |
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.
Отметим полученные точки («нули функции») на системе координат.
Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
Для каждого выбранного значения « x » рассчитаем « y ».
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
x0 =
| −b |
| 2a |
x0 =
| −(−6) |
| 2 · (−3) |
=
| 6 |
| −6 |
= −1
y0(−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
x1;2 =
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
x1;2 =
| −6 ± √ 36 − 48 |
| 2 |
x1;2 =
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.
Квадратичная функция и её график
Парабола является графиком квадратичной функции, которая задается формулой y = ax 2 + bx + c.
Нарисовать параболу можно, используя таблицу значений, в которой мы выбираем произвольный х и находим у. Но не всегда этот способ является самым рациональным.
Начнем, как всегда, с простого)
Стандартная парабола.
На координатной плоскости отмечаем эти точки и чертим параболу.
Начало координат тоже является вершиной этой параболы, как и в предыдущем случае, но ветви уже будут направлены вниз:
Если у тебя черный пояс по рисованию стандартных парабол, то следующий раздел пройдет у тебя «на ура».
Параболы со смещенной вершиной.
Зачем я начала статью со стандартной параболы? Ответ прост. Графиком любой квадратичной функции y = ±x 2 + bx + c (обязательно коэффициент перед х 2 должен равняться ±1) является стандартной параболой, только вот вершины этих парабол не будут находится в начале координат.
Чтобы начертить подобные параболы нужно сначала узнать, где находится вершина.
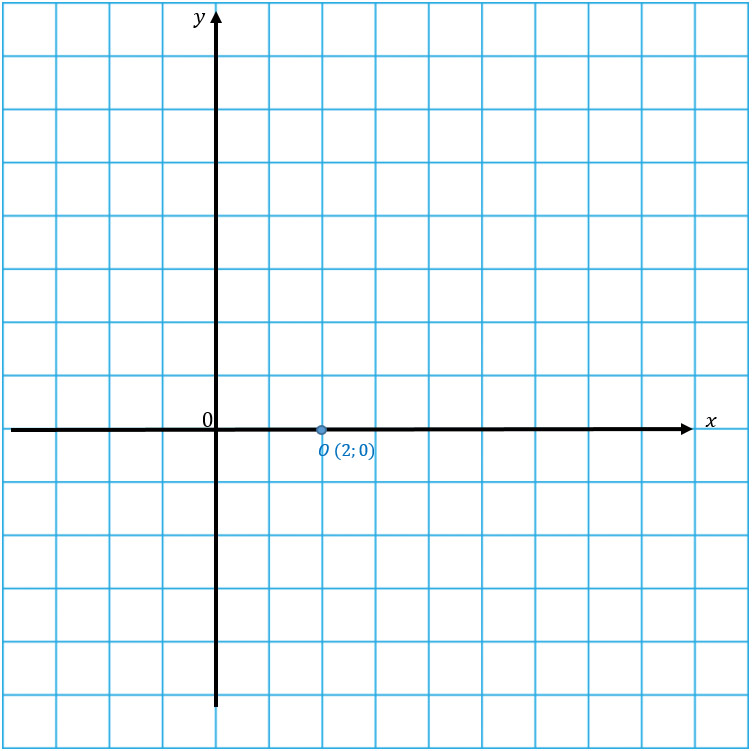
Пусть вершиной параболы будет точка О с координатами (x1; y1). Тогда найти эти координаты можно по формулам:
Кстати, можно найти координаты вершины и другим способом.
Координату хО находим по той же формуле, а координату уО можно найти подстановкой координаты хО в функцию.
Без примера не обойтись)
Найдем сначала вершину параболы двумя способами, чтобы убедится, что оба способа рабочие.
1 способ: по формулам.
2 способ: подстановкой.
Одну координаты мы уже нашли по формуле. Подставляем ее в исходную функцию.
Параболы-стройняшки и параболы-пухляшки.
Удивительно, но числовой коэффициент перед х 2 оказывается влияет на стройность и полноту парабол.
Если числовой коэффициент лежит в промежутке (-1; 0) ∪ (0; 1), то парабола будет более обширно смотреться на координатной плоскости.
Не веришь? Давай проверим! Для примера возьмем две функции:
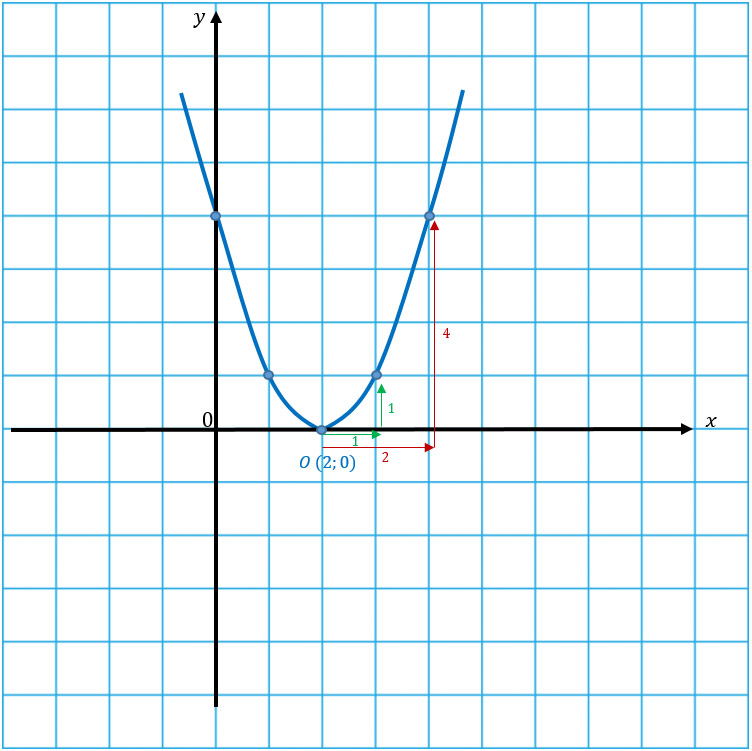
К сожалению, здесь схитрить не получится: обе параболы нестандартные и для обеих необходимо создать таблицы значений. Но перед эти определимся с их вершинами.
Переходим к таблицам значений.
| x | 0 | 2 | 4 | 6 | 8 |
| y | 3 | 6 | 7 | 6 | 3 |
| x | -1,5 | -1 | -0,25 | 0 | 1 |
| y | -3 | 1 | 4,5 | 3 | -3 |
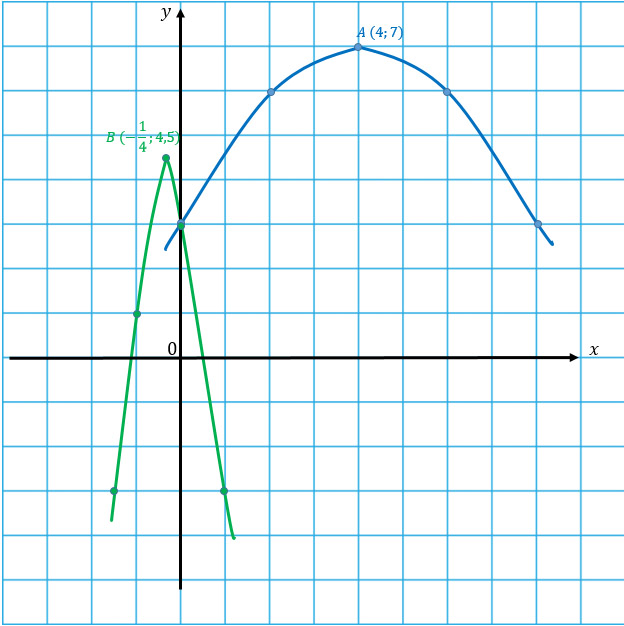
Чертим обе параболы по получившимся координатам.
Вот о чем я и говорила) Перед тобой парабола-стройняшка и парабола-пухляшка во всей красе.
Практикум по параболам.
Теорию о параболах можно еще писать и дальше, но тебя, скорее всего, интересует практика по графикам.
Поскольку речь идет о параболах, то с параболами мы и будем сейчас возиться.
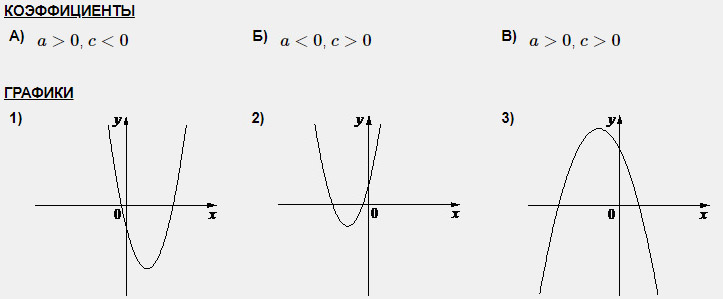
Задание 1. На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с отрицателен, то график пересекает ось Оу ниже нуля. Подходит график 1.
Б) Если коэффициент а отрицателен, то ветви направлены вниз; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 3.
В) Если коэффициент а положителен, то ветви направлены вверх; если коэффициент с положителен, то график пересекает ось Оу выше нуля. Подходит график 2.
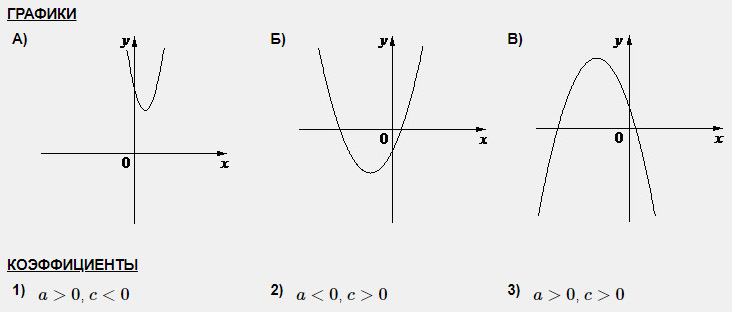
Задание 2 (наоборот). На рисунке изображены графики функций вида y = ax 2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
А) Ветви направлены вверх, значит а > 0; график пересекает ось Оу выше нуля, значит и с > 0. Подходит вариант под номером 3.
Б) Ветви направлены вверх, значит а > 0; график пересекает ось Оу ниже нуля, значит и с 0. Подходит вариант под номером 2.
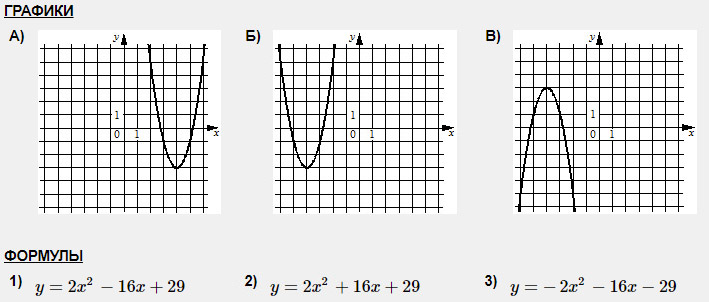
Задание 3. Установите соответствие между графиками и их функциями.
Дальше рекомендую отработанную годами технику. Она минимизирует твои ошибки, если ты, конечно, умеешь считать)
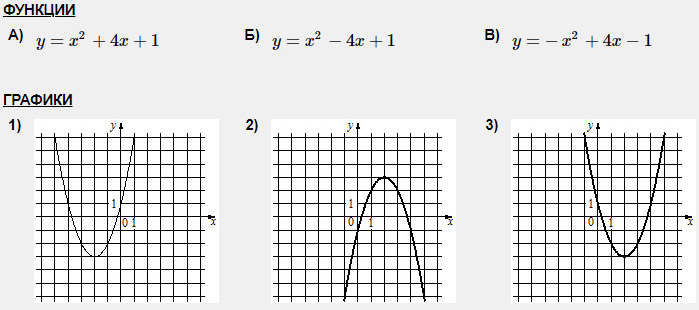
Задание 4 (наоборот, но принципе тот же). Установите соответствие между функциями и их графиками.
На графике 1 выбираем точку. Вершина снова четкая, но для разнообразия давайте возьмем другую точку, например, точку с координатами (-4; 1). Будь внимателен и смотри, чтобы точно такой же точки не было на третьем графике!
Квадратичная функция.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax 2 + bx + c = 0·x 2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x 2 − 2x или x 2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x 2 − 2x = 3x 2 − 2x + 0 и x 2 + 5 = x 2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax 2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax 2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax 2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Это представление удобно использовать при построении графика и изучении свойств квадратичной функции действительного переменного.

Графиком квадратичной функции является парабола, вершина которой находится в точке 
Парабола обладает еще одним интересным свойством, которое также используется как её определение.
Парабола представляет собой множество точек плоскости, расстояние от которых до определенной точки плоскости, называемой фокусом параболы, равно расстоянию до определенной прямой, называемой директрисой параболы.
Построить эскиз графика квадратичной функции можно по характерным точкам.
Например, для функции y = x 2 берем точки
| x | 0 | 1 | 2 | 3 |
| y | 0 | 1 | 4 | 9 |
Соединяя их от руки, строим правую половинку параболы. Левую получаем симметричным отраженим относительно оси ординат.
Для построения эскиза графика квадратичной функции общего вида в качестве характерных точек удобно брать координаты её вершины, нули функции (корни уравнения), если они есть, точку пересечения с осью ординат (при x = 0, y = c) и симметричную ей относительно оси параболы точку (−b/a; c).
| x | −b/2a | x1 | x2 | 0 | −b/a |
| y | −(b 2 − 4ac)/4a | 0 | 0 | с | с |
| при D ≥ 0 | |||||
Производная квадратичной функции вычисляется по формуле (ax 2 + bx + c)’ = 2ax + b.
Формулы для такого перехода можно выучить наизусть, а можно научиться выделять полный квадрат из трёхчлена с заданными коэффициентами. Это умение весьма полезно также для решения некоторых уравнений и неравенств, для вычисления интегралов и т.д.
Итак, чтобы построить график функции y = 3x 2 − 5x + 2 из графика y = x 2 нужно последний сдвинуть по оси Ox вправо на 5/6 ≈ 0,83 единицы. Затем растянуть вдоль оси Oy в 3 раза и, наконец, опустить по оси Oy на 1/12 ≈ 0,08 единицы.
Посмотрите, что получилось.
Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.
Преобразуем выражение с выделением полного квадрата: 
Строим график функции 
Видеоуроки с параболой.
Графики квадратичной функции и коэффициенты квадратного трёхчлена.
Положение и вид параболы в зависимости от знака и значения параметра c.
Построение параболы по характерным точкам.
Быстрое построение параболы как графика квадратичной функции.
Другие случаи. Примеры построения.
Задачи на анализ графика квадратичной функции.
Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.