Что такое arctg в физике

Что такое arctg в физике

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

К понятиям арксинус, арккосинус, арктангенс, арккотангенс учащийся народ относится с опаской. Не понимает он эти термины и, стало быть, не доверяет этой славной семейке.) А зря. Это очень простые понятия. Которые, между прочим, колоссально облегчают жизнь знающему человеку при решении тригонометрических уравнений!

Сомневаетесь насчёт простоты? Напрасно.) Прямо здесь и сейчас вы в этом убедитесь.

Разумеется, для понимания, неплохо бы знать, что такое синус, косинус, тангенс и котангенс. Да их табличные значения для некоторых углов. Хотя бы в самых общих чертах. Тогда и здесь проблем не будет.

Что означает выражение

И всё.

arc sin 0,4
угол, синус которого равен 0,4

Как пишется, так и слышится.) Почти. Приставка arc означает дуга (слово арка знаете?), т.к. древние люди вместо углов использовали дуги, но это сути дела не меняет. Запомните эту элементарную расшифровку математического термина! Тем более, для арккосинуса, арктангенса и арккотангенса расшифровка отличается только названием функции.

Верно. Выражение arccos1,8 не имеет смысла. И запись такого выражения в какой-нибудь ответ изрядно повеселит проверяющего.)

Внимание! Элементарная словесная и осознанная расшифровка арков позволяет спокойно и уверенно решать самые различные задания. А в непривычных заданиях только она и спасает.

Например: что такое arcsin 0,5?

Или, более солидно, через радианы:

Всё, можно забыть про арксинус и работать дальше с привычными градусами или радианами.

Если вы осознали, что такое арксинус, арккосинус. Что такое арктангенс, арккотангенс. То легко разберётесь, например, с таким монстром.)

Достаточно сообразить, что:

и всё. Заменяем все арки на значения в радианах, всё посокращается, останется посчитать, сколько будет 1+1. Это будет 2.) Что и является правильным ответом.

Вот таким образом можно (и нужно) переходить от арксинусов, арккосинусов, арктангенсов и арккотангенсов к обычным градусам и радианам. Это здорово упрощает страшные примеры!

Частенько, в подобных примерах, внутри арков стоят отрицательные значения. Типа, arctg(-1,3), или, к примеру, arccos(-0,8). Это не проблема. Вот вам простые формулы перехода от отрицательных значений к положительным:

Нужно вам, скажем, определить значение выражения:

Это можно и по тригонометрическому кругу решить, но вам не хочется его рисовать. Ну и ладно. Переходим от отрицательного значения внутри арккосинуса к положительному по второй формуле:

Внутри арккосинуса справа уже положительное значение. То, что

вы просто обязаны знать. Остаётся подставить радианы вместо арккосинуса и посчитать ответ:

Ограничения на арксинус, арккосинус, арктангенс, арккотангенс.

Грамотный человек знает, что синус равен 0,5 не только у угла 30°! Так как:

С этими ограничениями надо разобраться основательно. Тем более, что это дело простое.) Запоминаем:

Запомнить эти диапазоны очень легко по картинкам. Тригонометрический круг вам в помощь!) Для арксинуса:

Теперь, я думаю, понятно, что arcsin 0,5 = 30°. И только 30°! Так как углы 150°, 390°, 510° и т.д., которые тоже дают синус, равный 0,5, арксинусами быть не могут. Они выпадают из разрешённого диапазона.

Уже проще, правда?) Ну и, аналогичная картинка для арккосинуса и арккотангенса (при наведённом курсоре):

Надеюсь, зрительная память вас спасёт, если что. )

Вопрос резонный. В математике просто так, чисто для красоты, ничего не бывает. Только по острой необходимости!) А вы попробуйте ответить на такой вопрос:

У какого угла синус равен 0,4?

Для ответа в градусах или радианах вам придётся открывать таблицы Брадиса, или включать солидный калькулятор. Искать там значение синуса, равное (примерно!) 0,4 и смотреть, какой же угол имеет этот синус. После тяжких трудов вы определите, что это угол примерно 23 градуса и 36 минут. Про радианы я вообще молчу. )

Если вы осознали этот забавный факт, то легко ответите на все подобные вопросы:

А можно записать (приблизительно) тот же самый угол через градусы. Это будет:

≈ 23,57817847820183110402. °

Осознали простой и важный смысл арков? Тогда порешаем самостоятельно. Примерчики от устных до хитрых.)

Источник

Арктангенс и арккотангенс. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти арксинус и арккосинус от числа. Результат можно видеть как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Арктангенс и арккотангенс − теория, примеры и решения

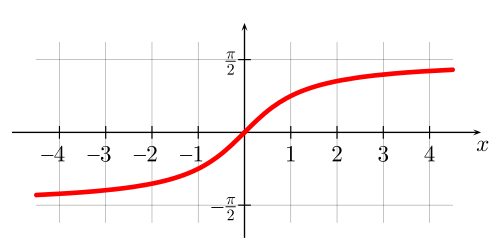
Функция арктангенс и ее график

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

, , , и т.д.

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

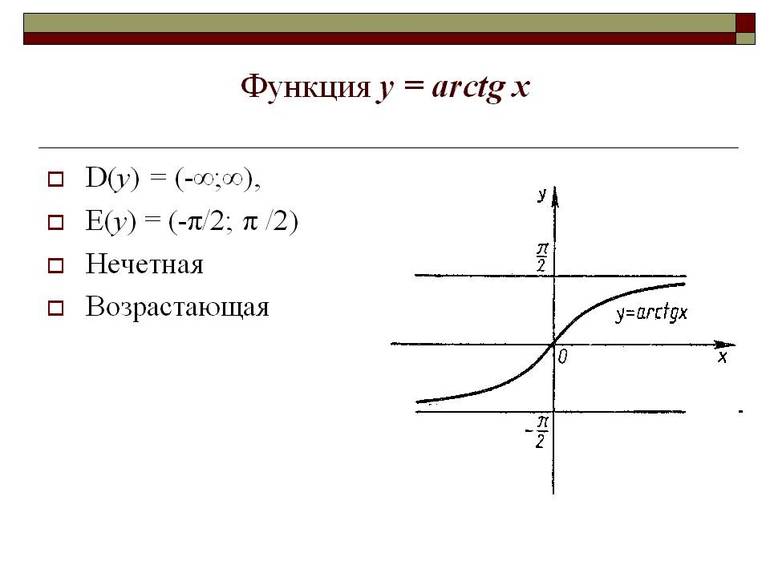
Свойства функции арктангенс.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

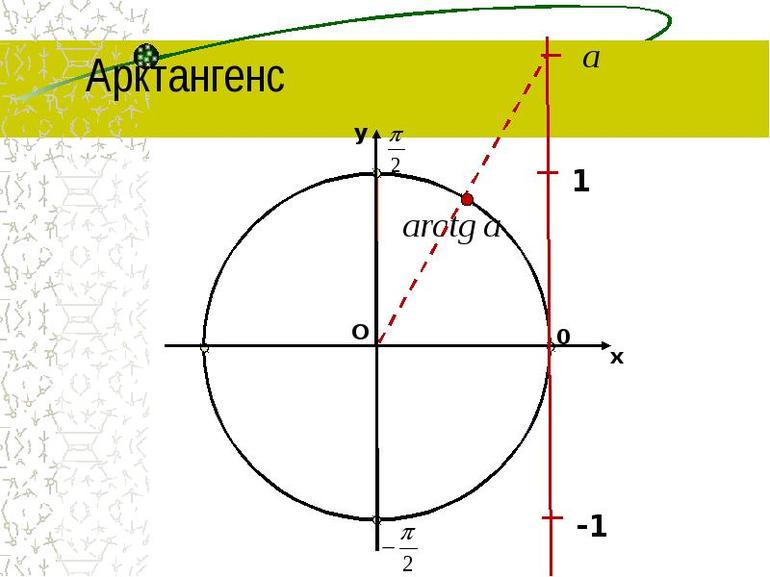
Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OM_t1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OT_t пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

Источник

Как найти арктангенс: формула, функция, свойства

Понятие арктангенса

Область определения для функции \(y=\operatorname x\) распространяется на всю прямую с числами, не прерывается и обладает ограничениями. Такая функция строго возрастает на графике.

\(\operatorname \,(\operatorname \,x)=x, если при x\in <\mathbb R>,\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(D(\operatorname \,x)=(-\infty ;\infty )\) (область определения),

Функция arctg обладает следующими свойствами, которые полезно использовать при расчете:

Получение функции арктангенса

Предположим, что имеется некая функция:

Заметим, что эта функция имеет вид кусочно-монотонной. Такая ситуация наблюдается на любом участке области определения. В результате нельзя назвать функцией:

Это связано с нарушением условий однозначности. Проанализируем участок, где функция является возрастающей и имеет каждое значение лишь однажды:

Отрезок \(y=\operatorname \,x\) отличается тем, что здесь функция является монотонно возрастающей со всеми своими значениями, которые она принимает только однажды.

График арктангенса

Рассматриваемая аркфункция характеризуется определенным графиком. Изобразить арктангенс на координатной плоскости можно с помощью преображения графика, которому соответствует тангенс. В процессе требуется переместить между собой оси абсцисс и ординат.

График функции \(y=\operatorname \,x\) (можно построить в программе Эксель при вводе нужной формулы):

Арксинус, арккосинус, арктангенс и арккотангенс как число

Обратными функциями в тригонометрии называют такие функции, которые являются обратными к тригонометрическим функциям.

Существует несколько основных аркфункций:

Обратные тригонометрические функции обладают особыми наименованиями. Названия аркфункций формулируют путем приписывания к наименованию функции приставки «арк-».

Функции в тригонометрии отличаются периодичностью. В связи с этим обратные к ним функции обладают множеством значений в виде углов (дуг), для которых конкретная прямая функция определена соответствующим числом.

Под функцией \(\arcsin 1/2\) понимается множество углов \(\left ( \frac<\pi><6>, \frac<5 \pi><6>, \frac<13 \pi><6>, \frac<17 \pi> <6>\dots

(30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right ).\)

Если посчитать, синус перечисленных углов соответствует 1/2.

Если рассмотреть множество значений обратной тригонометрической функции, то можно получить ключевые ее значения. Данные значения подразумевают при упоминании арксинуса, арккосинуса и других аркфункций.

Тогда каждое из решений уравнения \(\sin x=\alpha\) допустимо записать, как:

\(x=(-1)^\arcsin \alpha +\pi n,

При нахождении ответов в процессе решения задач, в условии которых присутствуют такие функции, как: синус, косинус, тангенс, котангенс угла, обратные им функции — арксинус, арккосинус, арктангенс, арккотангенс — определяют угол. В том случае, когда речь в задании идет о тригонометрических функциях числа, то аркфункции также будут определяться в виде числа.

Арккосинус числа \(а \in [−1, 1]\) является числом \(t\in [0, \pi]\) с косинусом, равным а.

Арккотангенс числа а \(\in (−\infty, \infty)\) является числом \(t\in (0, \pi)\) с котангенсом, равным а. В данном случае используют знак бесконечности, когда речь идет об определении а.

Важно различать задачи, где аркфункции являются числами, а где — углами. Данное условие можно понять по контексту. Если указана обратная тригонометрическая функция а без каких-либо уточнений, то ее допускается определять, как аркфункцию а в виде угла или числа.

Источник

Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса

Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа

Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.

sin ( a r c sin a ) = a

Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.

Пример 1. Свойства обратных тригонометрических функций

Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел

Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.

arcsin, arccos, arctg и arcctg противоположных чисел

Доказательство свойства арксинусов противоположных чисел завершено.

Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.

Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.

Сумма арксинуса и арккосинуса, арктангенса и арккотангенса

Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.

Сумма arcsin и arccos

Соответственно, для арктангенса и арккотангенса

Сумма arctg и arcctg

Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.

Пример 2. Сумма арксинуса и арккосинуса

Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса

Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса

Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.

Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.

Источник

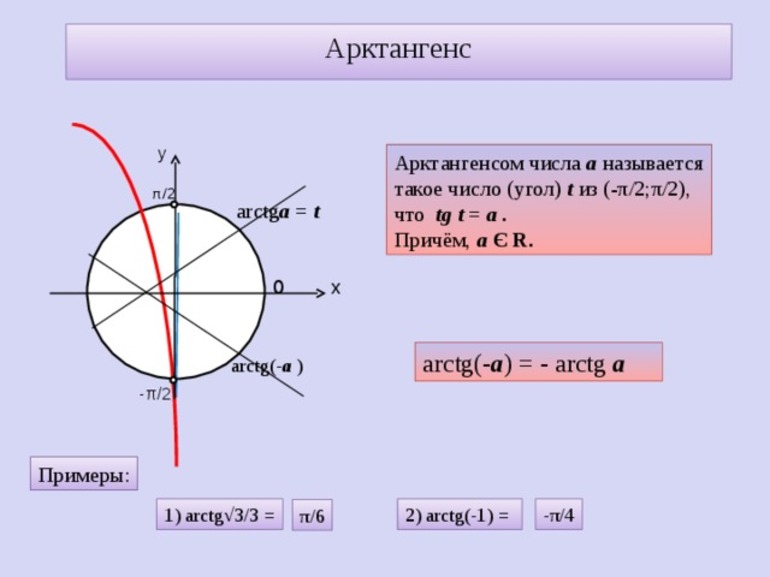
Арктангенс- определение, свойства и формулы

Чётность и возрастание

Чтобы получить график арктангенса, используется кривая тангенса путём замены местами осей ординат и абсцисс. Для устранения многозначности используется интервал, на котором функция монотонна. Это определение считается основным значением арктангенса. Если показатель отрицательный, значит функция нечётная.

Главное свойство arctg — бесконечность на его области определения (для числа х). Так как y = arctg x, где y равен нулю, тогда x = 0, значит и arctg 0. При выполнении расчётов используется таблица арктангенсов.

В ней указаны значения в градусах и радианах, при определённых данных аргумента. Если вычисления выполняются на математическом веб-ресурсе, пользователю предоставляется возможность бесплатно использовать онлайн-калькулятор и таблицу Брадиса. Можно вычислить синус, косинус, производную арктангенса в экселе либо с помощью языка программирования Паскаль.

Чтобы посчитать величину правильно, используются свойства функций. При помощи определения арксинуса выполняется уравнение sin (arcsin a)=a. Свойства других величин:

В первых двух свойствах соблюдается условие −1≤a≤1. Если значение а выходит за указанные пределы, тогда функции нет смысла определять. Учитывая свойства синуса арксинуса, нельзя записать sin (arcsin8)=8, так как выражение sin (arcsin8) не имеет смысла. Аналогичный ответ получается, если необходимо определить разность арккосинуса sqrt (квадратный корень) из пяти.

Противоположные числа

Формулы, с помощью которых производится расчёт связи между производными: arcsin (-a)=-arcsina, arccos (-a)=пи-arccosa, arctg (-a)=-arctga, arcctg (-a)=пи-arcctga. Должно соблюдаться условие −1≤a≤1. Если а принадлежит промежутку −∞ до +∞, тогда arctg (−a), и arcctg (−a).

Чтобы доказать первое отношение с противоположными числами, рассматривается определение arcsin (−a). Число либо угол находится в пределах −π/2-π/2 и синус, равный −a. Учитывая определение арксинуса, можно записать следующее равенство: −π/2≤arcsin a≤π/2.

Необходимо доказать, что sin (−arcsin a)=−a. Для этого рекомендуется придерживаться свойств противоположных углов. Из рассмотренных примеров можно сделать вывод: sin (−arcsin a)=−sin (arcsin a)=−a.

Аналогичным способом можно доказать, что arccos (−a)=π−arccos a. Используя определение производной функции, подтверждается, что π−arccos a — угол либо число, значение которого колеблется в пределах 0-π, а cos (π−arccos a)=−a. Придерживаясь определения арккосинуса числа, выполняется неравенство 0≤arccos a≤π.

Если средняя часть уравнения равняется −a, тогда, придерживаясь формулы приведения, записывается следующее равенство cos (π−arccos a)=−cos (arcos a). С помощью свойства производной косинуса завершается доказательство cos (π−arccos a)=−cos (arcos a)=−a. Аналогичной схемы рекомендуется придерживаться при рассмотрении свойств арккотангенсов и арктангенсов противоположных знаков. Плюс утверждения — возможность избавиться от вычисления производных функций отрицательных чисел.

Сложение величин

Свойство, согласно которому устанавливается связь между arccos arcsin числа а, и между arctg и arcctg переменной, записывается следующим образом: arcsina+arccosa=пи/2, arctga+arcctga=пи/2. Чтобы доказать первую часть равенства, где расписана сумма производных синуса и косинуса числа а, делённая на два, необходимо рассмотреть следующую запись: arcsin a=π/2−arccos a.

Основываясь на определение арксинуса, можно доказать, что выражение верно, когда π/2−arccos a — угол (цифровое значение), лежащий на промежутке −π/2 до π/2, а синус угла равен а. Чтобы показать такую действительность, используется определение арккосинуса и равенство 0≤arccos a≤π. Последнее выражение считается справедливым.

С учётом свойств неравенств, умножаются части на минус один, изменяются знаки. Полученные значения суммируются с числом π/2. Выполнив перечисленные действия, получается неравенство −π/2≤π/2−arccosa≤π/2. Чтобы показать, что sin (π/2−arccos a)=a, используется формула приведения, свойство производной функции косинус.

Доказано, что сумма arccos и arccos a равна π/2. Аналогично понадобится доказать, что сумма арккотангенса числа a и арктангенса равняется π/2. Главное предназначение таких свойств заключается в том, что они выражают арксинус через акрккосинус одного числа, а также арккотангенс через арктангенс и наоборот.

Примеры и задачи

Задания на свойства функций и их производных от числа либо угла можно решить с помощью разных программ: excel, pascal. Действия будут зависеть от условий задачи. Решение должно основываться на основные признаки, доказанные либо утверждённые равенства. Свойствам производных отвечают следующие выражения:

Равенства при определённых условий следуют из определений функций числа. Чтобы понять утверждения, необходимо доказать: arcsin (sin α)=α, при этом должно выполняться требование −π/2≤α≤π/2. Аналогичным образом доказываются оставшиеся свойства. Если обозначить sin α=а, которое находится на отрезке [−1, 1], тогда получится выражение arcsin (sin α)=α, то есть arcsin a=α. Известно из условий задач, что −π/2≤α≤π/2. При решении через а обозначили sin α.

Поэтому можно записать, что arcsin a=α, что эквивалентно определению производной функции синуса. Вывод: arcsin (sin α)=α при условии, что −π/2≤α≤π/2. Разные свойства, связанные с синусом и косинусом, тангенсом и котангенсом, можно применить на практике.

Запись arccos (cos α) правдивая, не только при условии, что 0≤α≤π. Выражение arccos (cos α)=α считается справедливым только при таком условии. Поэтому arccos (cos (−3π))=−3π не верно, так как −3π не принадлежит указанному отрезку. Схожие утверждения логичны и для arcctg (ctg α), arctg (tg α).

Используя определение всех функций, их признаки, тригонометрические формула можно получить другие равенства и уравнения, в которых отображается связь между arcsin, arcctg, arctg и arccos. Чтобы быстро решать задачи на данную тематику, рекомендуется выучить некоторые утверждённые равенства (arcsin 0=0, arccos 1=0, как угол arccos (-1)=180 градусов). Они описаны в специальных таблицах, которые можно найти в глобальной сети либо в учебниках по математике.

Источник