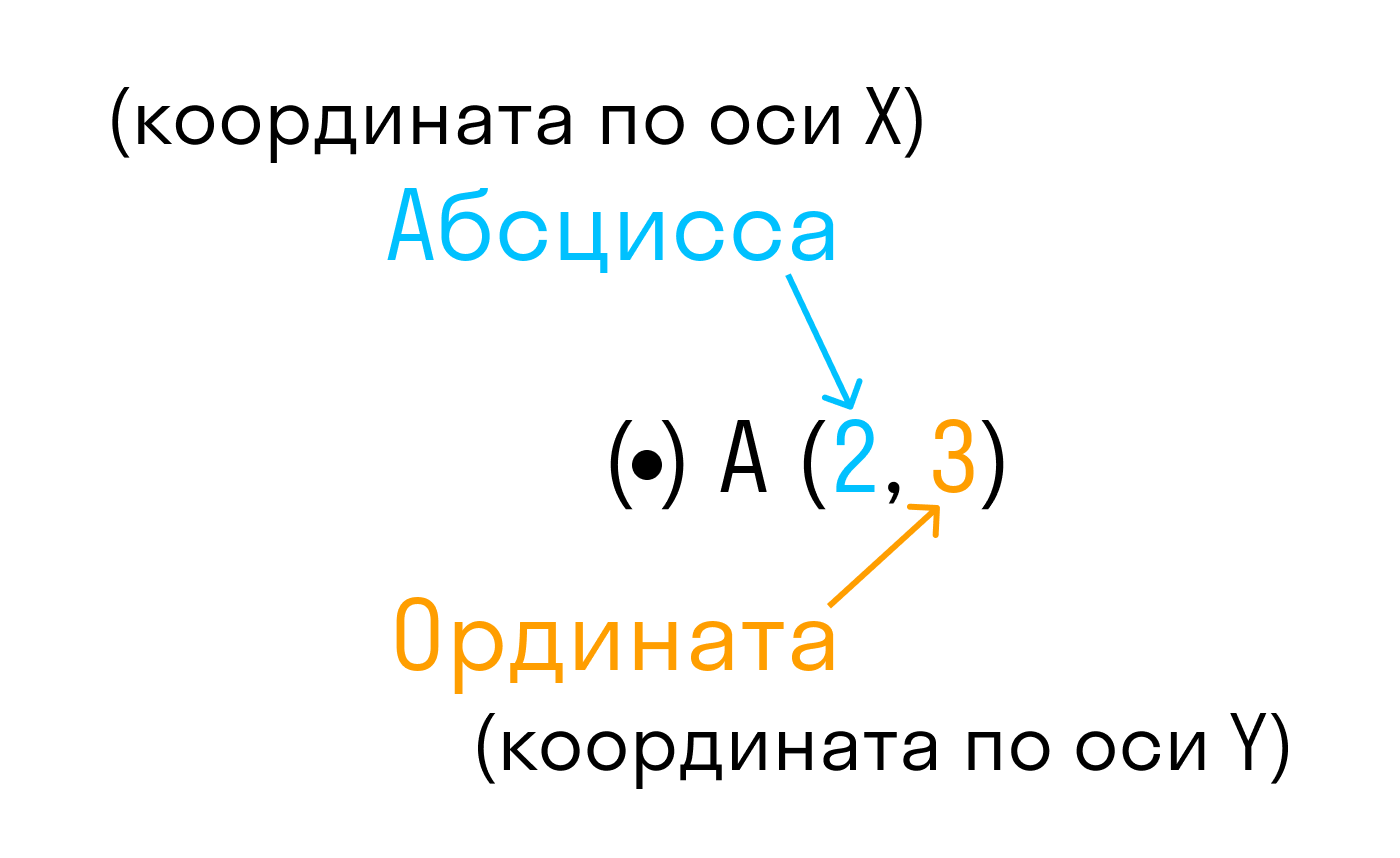
Что такое абсцисса точки ордината точки
Как найти координаты точки?
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
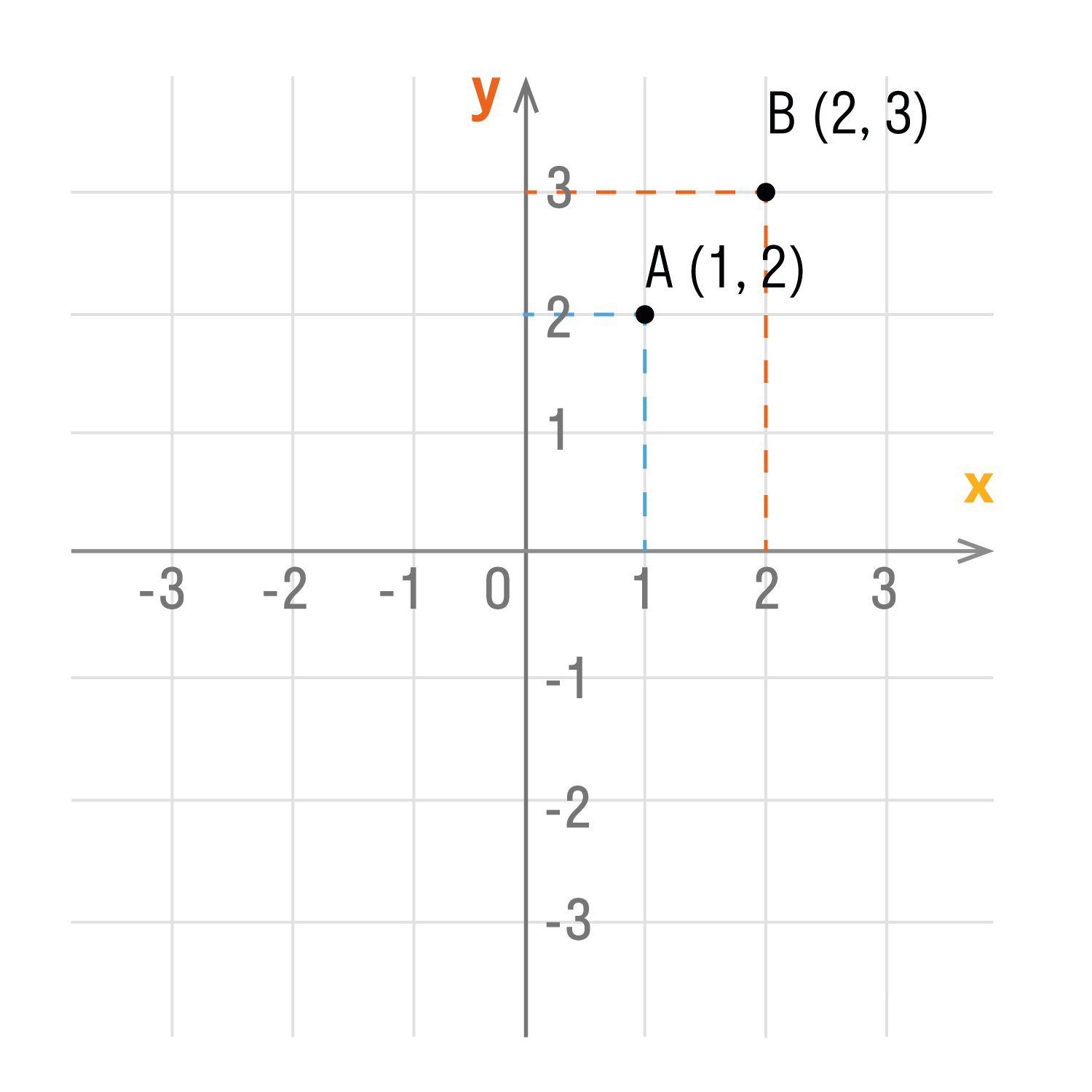
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
Способ второй. Как определить положение точки D (-4, 2):
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Прямоугольная система координат. Ось абсцисс и ординат
Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
В обычном использовании абсцисса относится к горизонтальному (Икс) ось и ордината относится к вертикали (у) оси стандартного двумерного графа.
В абсцисса точки подписано мера его проекции на первичную ось, абсолютное значение которой представляет собой расстояние между проекцией и началом координат оси, а знак задается положением на проекции относительно начала координат (до: отрицательное; после: положительное).
В ордината точки подписано мера проекции на вторичную ось, абсолютное значение которой представляет собой расстояние между проекцией и началом координат оси, а знак задается положением на проекции относительно начала координат (до: отрицательное; после: положительное).
Содержание
Этимология
Хотя слово «абсцисса» (лат. «Linea abscissa», «отрезанная линия») использовалось по крайней мере с тех пор. De Practica Geometrie опубликовано в 1220 г. Фибоначчи (Леонардо Пизанский), его использование в современном понимании может быть связано с венецианским математиком Стефано дельи Анджели в его работе Miscellaneum Hyperbolicum, et Parabolicum 1659 г. [1]
В его работе 1892 г. Vorlesungen über Geschichte der Mathematik («Лекции по истории математики«), том 2, немецкий язык историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Абсцисс in lateinischen Originalschriften. Vielleicht kommt das Wort в Uebersetzungen der Apollonischen Kegelschnitte vor, wo Buch I Satz 20 von ἀποτεμνομέναις die Rede ist, wofür es kaum ein entsprechenderes lateinisches Wort als абсцисса geben möchte. [2]
В то же время, предположительно, [Стефано дельи Анджели], что слово было введено в математический словарь, для которого будущее, особенно в аналитической геометрии, оказалось много припасено. […] Мы не знаем ранее употребления этого слова абсцисса в латинских оригинальных текстах. Может быть, это слово встречается в переводах Аполлонические коники, где [в] Книге I, главе 20 упоминается о ἀποτεμνομέναις, для которого вряд ли найдется более подходящее латинское слово, чем абсцисса.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
В несколько устаревшем варианте использования абсцисса точки может также относиться к любому числу, которое описывает местоположение точки на некотором пути, например параметр параметрическое уравнение. [3] При таком использовании абсциссу можно рассматривать как аналог координатной геометрии независимая переменная в математическая модель или поэкспериментируйте (с любыми ординатами, выполняющими роль, аналогичную зависимые переменные).
Обычно абсцисса относится к горизонтальной оси ( x ), а ордината относится к вертикальной оси ( y ) стандартного двухмерного графика.
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
СОДЕРЖАНИЕ
Этимология
В своей работе 1892 года « Vorlesungen über die Geschichte der Mathematik» (« Лекции по истории математики »), том 2, немецкий историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht Kommt Дас Сусло в Uebersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
В обычном использовании абсцисса относится к горизонтальному (Икс) ось и ордината относится к вертикали (у) оси стандартного двумерного графа.
В абсцисса точки подписано мера его проекции на первичную ось, абсолютное значение которой представляет собой расстояние между проекцией и началом координат оси, а знак задается положением на проекции относительно начала координат (до: отрицательное; после: положительное).
В ордината точки подписано мера проекции на вторичную ось, абсолютное значение которой представляет собой расстояние между проекцией и началом координат оси, а знак задается положением на проекции относительно начала координат (до: отрицательное; после: положительное).
Содержание
Этимология
Хотя слово «абсцисса» (лат. «Linea abscissa», «отрезанная линия») использовалось по крайней мере с тех пор. De Practica Geometrie опубликовано в 1220 г. Фибоначчи (Леонардо Пизанский), его использование в современном понимании может быть связано с венецианским математиком Стефано дельи Анджели в его работе Miscellaneum Hyperbolicum, et Parabolicum 1659 г. [1]
В его работе 1892 г. Vorlesungen über Geschichte der Mathematik («Лекции по истории математики«), том 2, немецкий язык историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Абсцисс in lateinischen Originalschriften. Vielleicht kommt das Wort в Uebersetzungen der Apollonischen Kegelschnitte vor, wo Buch I Satz 20 von ἀποτεμνομέναις die Rede ist, wofür es kaum ein entsprechenderes lateinisches Wort als абсцисса geben möchte. [2]
В то же время, предположительно, [Стефано дельи Анджели], что слово было введено в математический словарь, для которого будущее, особенно в аналитической геометрии, оказалось много припасено. […] Мы не знаем ранее употребления этого слова абсцисса в латинских оригинальных текстах. Может быть, это слово встречается в переводах Аполлонические коники, где [в] Книге I, главе 20 упоминается о ἀποτεμνομέναις, для которого вряд ли найдется более подходящее латинское слово, чем абсцисса.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
В несколько устаревшем варианте использования абсцисса точки может также относиться к любому числу, которое описывает местоположение точки на некотором пути, например параметр параметрическое уравнение. [3] При таком использовании абсциссу можно рассматривать как аналог координатной геометрии независимая переменная в математическая модель или поэкспериментируйте (с любыми ординатами, выполняющими роль, аналогичную зависимые переменные).