Что такое абсцисса точки касания
Уравнение касательной к графику функции (ЕГЭ 2022)
Чтобы разобраться с этой темой, нужно знать что такое производная.
Сейчас проверим, знаешь ли ты ее… 🙂
Найди приращение функции \( y=<
Должно получиться \( \Delta y=\Delta x\left( \Delta x+2x+2 \right)\).
А теперь найди производную функции \( y\left( x \right)=3<<\sin >^<2>>\sqrt
Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме «Производная» и проштудировать ее еще раз.
Знаю, тема очень большая, но иначе нет смысла идти дальше…
А если ты справился, то в путь!
Уравнение касательной к графику функции — коротко о главном
Геометрический смысл производной
Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:
Уравнение касательной
Уравнение касательной к графику функции \( f\left( x \right)\) в точке \( <
Алгоритм действий для нахождения уравнения касательной
| Алгоритм | Пример: \( f\left( x \right)=< |
| 1. Вычислим \( f\left( < | \( f\left( < |
| 2. Найдем формулу производной функции \( | \( |
| 3. Вычислим \( | \( |
| 4. Подставим \( < | \( \begin |
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции \( y=f\left( x \right)\):
Выберем на линии графика некую точку \( A\). Пусть ее абсцисса \( <
Затем выберем близкую к точке \( A\) точку \( B\) с абсциссой \( <
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси \( Ox\) как \( \alpha \).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол \( \alpha \)?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – \( 180<>^\circ \), а минимально возможный – \( 0<>^\circ \).
Значит, \( \alpha \in \left[ 0<>^\circ ;180<>^\circ \right)\). Угол \( 180<>^\circ \) не включается, поскольку положение прямой в этом случае в точности совпадает с \( 0<>^\circ \), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку \( C\), чтобы прямая \( AC\) была параллельна оси абсцисс, а \( BC\) – ординат:
По рисунку видно, что \( AC=\Delta x\), а \( BC=\Delta f\).
Тогда отношение приращений:
(так как \( \angle C=90<>^\circ \), то \( \triangle ABC\) – прямоугольный).
Давай теперь уменьшать \( \Delta x\).
Тогда точка \( B\) будет приближаться к точке \( A\). Когда \( \Delta x\) станет бесконечно малым \( \left( \Delta x\to 0 \right)\), отношение \( \frac<\Delta f><\Delta x>\) станет равно производной функции в точке \( <
Что же при этом станет с секущей?
Точка \( B\) будет бесконечно близка к точке \( A\), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки \( A\), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси \( \displaystyle Ox\) назовем \( \varphi \). Тогда получится, что производная
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
За что отвечает коэффициент \( \displaystyle k\)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью \( \displaystyle Ox\)!
То есть вот что получается:
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы \( \alpha \) и \( \displaystyle \varphi \) тупые. А приращение функции \( \Delta f\) – отрицательное.
Получаем: \( \frac<-\Delta f><\Delta x>=-\
Снова устремим точку \( \displaystyle B\) к точке \( \displaystyle A\), и секущая \( \displaystyle AB\) примет предельное положение, то есть превратится в касательную к графику функции в точке \( \displaystyle A\).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции \( \displaystyle y=\mathsf
Найдите значение производной функции \( \displaystyle \mathsf
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle f’\left( x \right)=k=\
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси \( \displaystyle Ox\) – это \( \displaystyle \angle BAC\). Найдем тангенс этого угла:
Таким образом, производная функции \( \displaystyle \mathsf
Ответ: \( \displaystyle 1,2\).
Теперь попробуй сам.
Еще статью на геометрический смысл производной ты найдешь здесь: «Геометрический смысл производной«.
Решим два примера
Пример 1. На рисунке изображен график функции \( \displaystyle y=\mathsf
Пример 2. На рисунке изображен график функции \( \displaystyle y=\mathsf
Решение примера №1
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle k=f’\left( x \right)=\
Достроим треугольник со стороной \( \displaystyle AC\), лежащей на касательной.
Угол наклона касательной – это угол, отмеченный зеленым на графике.
Он тупой \( \left( >90<>^\circ \right)\), поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла).
Применим знания из тригонометрии:
Прямая является касательной к графику функции
Задачи несложные, но они требуют чёткого понимания геометрического смысла производной. Это теоретическая основа для решения подобных задач (и подобных им), и без этой основы никак нельзя. Рекомендую ознакомиться со статьями « Геометричесий смысл произвоной. Часть 1 » и « Геометрический смысл производной. Часть 2 ».
Рассмотрим две задачи:
Прямая у = 4х + 8 параллельна касательной к графику функции
Найдите абсциссу точки касания.
Из геометрического смысла производной мы знаем, что значение производной в точке касания равно угловому коэффициенту касательной.
Известно, что угловые коэффициенты параллельных прямых равны, значит угловые коэффициенты прямой у = 4х + 8 и касательной равны 4.
Угловой коэффициент прямой вида у = kх + b это число k.
Таким образом, абсцисса точки касания находится из уравнения:
Он предельно прост, но не всегда работает. Строим на координатной плоскости график у = х 2 – 5х + 7, строим прямую у = 4х + 8, далее строим (параллельным переносом) параллельную ей прямую касающуюся параболы, и в некоторых задачах вы визуально сможете определить абсциссу точки касания.
Отмечу, что таким способом можно решить задачу, если абсцисса целое число или целое с половиной, например 1,5; – 2,5; –3,5 и так далее. Если же точка пересечения «непонятна», то есть, нельзя точно и уверенно определить абсциссу (например, визуально сложно определить 3,2; 5,7 …), то точное решение даст первый способ.
Если вы решили задачу этим способом и уверены в правильности решения, обязательно сделайте проверку. Подставьте полученную абсциссу в оба исходных уравнения, должны получится равные значения функций (ордината точки пересечения).
Прямая у = 7х – 8 параллельна касательной к графику функции
Найдите абсциссу точки касания.
Прямая у = 6х + 4 является касательной к графику функции
у = х 3 – 3х 2 + 9х + 3
Найдите абсциссу точки касания.
Из геометрического смысла производной функции известно, что она (производная) равна угловому коэффициенту касательной.
Известно, что угловой коэффициент прямой вида у = kх + b это число k.
Значит, угловой коэффициент прямой у = 6х + 4 равен 6. Таким образом,
Решая квадратное уравнение, получим:
Получили два равных корня. Таким образом, абсцисса точки касания равна 1.
Прямая у = – 4х – 11 является касательной к графику функции
у = х 3 + 7х 2 + 7х – 6
Найдите абсциссу точки касания
В данной рубрике продолжим рассматривать задачи, не пропустите!
Уравнение касательной к графику функции
п.1. Уравнение касательной
п.2. Алгоритм построения касательной
На входе: уравнение кривой \(y=f(x)\), абсцисса точки касания \(x_0\).
Шаг 1. Найти значение функции в точке касания \(f(x_0)\)
Шаг 2. Найти общее уравнение производной \(f’ (x)\)
Шаг 3. Найти значение производной в точке касания \(f'(x_0 )\)
Шаг 4. Записать уравнение касательной \(y=f’ (x_0)(x-x_0)+f(x_0)\), привести его к виду \(y=kx+b\)
На выходе: уравнение касательной в виде \(y=kx+b\)
 | Пусть \(f(x)=x^2+3\). Найдем касательную к этой параболе в точке \(x_0=1\). |
п.3. Вертикальная касательная
Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода \(x_0\notin D\), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку \(x_0\in D\), входящую в область определения. График функции и касательная имеют одну общую точку \((x_0,y_0)\).
Вертикальные касательные характерны для радикалов вида \(y=\sqrt[n]
 | Пусть \(f(x)=\sqrt[5] Найдем касательную к этой кривой в точке \(x_0=1\). |
\(f(x_0)=\sqrt[5]<1-1>+1=1\)
\(f'(x)=\frac15(x-1)^<\frac15-1>+0=\frac15(x-1)^<-\frac45>=\frac<1><5(x-1)^<\frac45>> \)
\(f'(x_0)=\frac<1><5(1-1)^<\frac45>>=\frac10=+\infty\)
В точке \(x_0\) проходит вертикальная касательная.
Её уравнение: \(x=1\)
Ответ: \(y=2x+2\)
п.4. Примеры
Пример 1. Для функции \(f(x)=2x^2+4x\)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.
б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.
в) найдите, в какой точке касательная будет параллельна прямой \(2x+y-6=0\). Напишите уравнение этой касательной.
 | Найдем угловой коэффициент заданной прямой: \(y=-2x+6\Rightarrow k=-2\). Касательная должна быть параллельной, значит, её угловой коэффициент тоже \(k=-2\). Получаем уравнение: \begin |
г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.
 | У горизонтальной прямой \(k=0\). Получаем уравнение: \(f'(x_0)=0\). \begin |
Ответ: а) \(y=4x\) и \(y=-4x-8\); б) \(y=x-\frac98\); в) \(2x+y+\frac92=0\); г) \(y=-2\)
Пример 3*. Найдите точку, в которой касательная к графику функции \(f(x)=\frac
Угловой коэффициент данной прямой \(k_1=11\).
Угловой коэффициент перпендикулярной прямой \(k_2=-\frac<1>
Уравнение касательной при \(x_0=-14\) \begin
Ответ: точка касания (-14;-4), уравнение \(y=-\frac
и точка касания (8;-2), уравнение \(-\frac
Пример 4*. Найдите уравнения общих касательных к параболам \(y=x^2-5x+6\) и \(y=x^2+x+1\). Укажите точки касания.
Пример 5*. Докажите, что кривая \(y=x^4+3x^2+2x\) не пересекается с прямой \(y=2x-1\), и найдите расстояние между их ближайшими точками.
Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом \(k=2\), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой \(y=2x-1\).
Строим уравнение касательной. По условию: \(f'(x)=4x^3+6x+2=2\) \begin
Уравнение касательной: \(y=2(x-0)+0=2x\)
 | Ищем расстояние между двумя параллельными прямыми: \(y=2x\) и \(y=2x-1\). Перпендикуляр из точки (0;0) на прямую \(y=2x-1\) имеет угловой коэффициент \(k=-\frac12\), его уравнение: \(y=-\frac12 x+b\). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и \(b=0\). |
Уравнение перпендикуляра: \(y=-\frac x2\).
Находим точку пересечения прямой \(y=2x-1\) и перпендикуляра \(y=-\frac x2\): \begin
Находим расстояние \(OA=\sqrt<0,4^2+(-0,2)^2>=0,2\sqrt<2^2+1^2>=\frac<\sqrt<5>><5>\)
Ответ: \(\frac<\sqrt<5>><5>\)
Уравнение касательной к графику функции
Статья опубликована при поддержке Гостиничного комплекса «ИТАКА+». Останавливаясь в городе судостроителей Северодвинске, вы не столкнетесь с проблемой поиска временного жилья. Тут, на сайте гостиничного комплекса «ИТАКА+» http://itakaplus.ru, вы сможете легко и быстро снять квартиру в городе, на любой срок, с посуточной оплатой.
На современном этапе развития образования в качестве одной из основных его задач выступает формирование творчески мыслящей личности. Способность же к творчеству у учащихся может быть развита лишь при условии систематического привлечения их к основам исследовательской деятельности. Фундаментом для применения учащимися своих творческих сил, способностей и дарований являются сформированные полноценные знания и умения. В связи с этим проблема формирования системы базовых знаний и умений по каждой теме школьного курса математики имеет немаловажное значение. При этом полноценные умения должны являться дидактической целью не отдельных задач, а тщательно продуманной их системы. В самом широком смысле под системой понимается совокупность взаимосвязанных взаимодействующих элементов, обладающая целостностью и устойчивой структурой.
Рассмотрим методику обучения учащихся составлению уравнения касательной к графику функции. По существу, все задачи на отыскание уравнения касательной сводятся к необходимости отбора из множества (пучка, семейства) прямых тех из них, которые удовлетворяют определенному требованию – являются касательными к графику некоторой функции. При этом множество прямых, из которого осуществляется отбор, может быть задано двумя способами:
а) точкой, лежащей на плоскости xOy (центральный пучок прямых);
б) угловым коэффициентом (параллельный пучок прямых).
В связи с этим при изучении темы «Касательная к графику функции» с целью вычленения элементов системы нами были выделены два типа задач:
1) задачи на касательную, заданную точкой, через которую она проходит;
2) задачи на касательную, заданную ее угловым коэффициентом.
Обучение решению задач на касательную осуществлялось при помощи алгоритма, предложенного А.Г. Мордковичем [2]. Его принципиальное отличие от уже известных заключается в том, что абсцисса точки касания обозначается буквой a (вместо x0), в связи с чем уравнение касательной приобретает вид
(сравните с y = f(x0) + f ‘(x0)(x – x0)). Этот методический прием, на наш взгляд, позволяет учащимся быстрее и легче осознать, где в общем уравнении касательной записаны координаты текущей точки, а где – точки касания.
Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить буквой a абсциссу точки касания.
2. Найти f(a).
3. Найти f ‘(x) и f ‘(a).
4. Подставить найденные числа a, f(a), f ‘(a) в общее уравнение касательной y = f(a) = f ‘(a)(x – a).
Этот алгоритм может быть составлен на основе самостоятельного выделения учащимися операций и последовательности их выполнения.
Практика показала, что последовательное решение каждой из ключевых задач при помощи алгоритма позволяет формировать умения написания уравнения касательной к графику функции поэтапно, а шаги алгоритма служат опорными пунктами действий. Данный подход соответствует теории поэтапного формирования умственных действий, разработанной П.Я. Гальпериным и Н.Ф. Талызиной [3].


Решение. Точка M(3; – 2) является точкой касания, так как
1. a = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f ‘(x) = x 2 – 4, f ‘(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.
Задача 2. Напишите уравнения всех касательных к графику функции y = – x 2 – 4x + 2, проходящих через точку M(– 3; 6).

1. a – абсцисса точки касания.
2. f(a) = – a 2 – 4a + 2.
3. f ‘(x) = – 2x – 4, f ‘(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.
Касательная проходит через точку M(– 3; 6), следовательно, ее координаты удовлетворяют уравнению касательной.
6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a1 = – 4, a2 = – 2.
Если a = – 4, то уравнение касательной имеет вид y = 4x + 18.
Если a = – 2, то уравнение касательной имеет вид y = 6.
Задача 3. Напишите уравнения всех касательных к графику функции y = x 3 – 3x 2 + 3, параллельных прямой y = 9x + 1.
1. a – абсцисса точки касания.
2. f(a) = a 3 – 3a 2 + 3.
3. f ‘(x) = 3x 2 – 6x, f ‘(a) = 3a 2 – 6a.

y = 9x + 8 – уравнение касательной;
y = 9x – 24 – уравнение касательной.

Решение. Из условия f ‘(a) = tg 45° найдем a: a – 3 = 1 ^ a = 4.
1. a = 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f ‘(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).
y = x – 7 – уравнение касательной.
Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач. Рассмотрим в качестве примера следующие две задачи.

Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.
1. a = 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f ‘(x) = 4x – 5, f ‘(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.
Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то 
Это значит, что угловой коэффициент второй касательной равен 
Дальнейшее решение сводится к ключевой задаче 3.
Пусть B(c; f(c)) есть точка касания второй прямой, тогда
1.
– абсцисса второй точки касания.
2.
3.
4.
– уравнение второй касательной.
Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k1•k2 = – 1.
2. Напишите уравнения всех общих касательных к графикам функций

1. Пусть c – абсцисса точки касания, лежащей на графике функции

2.
3. f ‘(c) = c.
4.
Так как касательные общие, то
Итак, y = x + 1 и y = – 3x – 3 – общие касательные.
Основная цель рассмотренных задач – подготовить учащихся к самостоятельному распознаванию типа ключевой задачи при решении более сложных задач, требующих определенных исследовательских умений (умения анализировать, сравнивать, обобщать, выдвигать гипотезу и т. д.). К числу таких задач можно отнести любую задачу, в которую ключевая задача входит как составляющая. Рассмотрим в качестве примера задачу (обратную задаче 1) на нахождение функции по семейству ее касательных.
3. При каких b и c прямые y = x и y = – 2x являются касательными к графику функции y = x 2 + bx + c?
Составим и решим систему уравнений
Ответ:
Задачи для самостоятельного решения
1. Напишите уравнения касательных, проведенных к графику функции y = 2x 2 – 4x + 3 в точках пересечения графика с прямой y = x + 3.
Ответ: y = – 4x + 3, y = 6x – 9,5.
2. При каких значениях a касательная, проведенная к графику функции y = x 2 – ax в точке графика с абсциссой x0 = 1, проходит через точку M(2; 3)?
3. При каких значениях p прямая y = px – 5 касается кривой y = 3x 2 – 4x – 2?
4. Найдите все общие точки графика функции y = 3x – x 3 и касательной, проведенной к этому графику через точку P(0; 16).
Ответ: A(2; – 2), B(– 4; 52).
5. Найдите кратчайшее расстояние между параболой y = x 2 + 6x + 10 и прямой
Ответ:
6. На кривой y = x 2 – x + 1 найдите точку, в которой касательная к графику параллельна прямой y – 3x + 1 = 0.
7. Напишите уравнение касательной к графику функции y = x 2 + 2x – | 4x |, которая касается его в двух точках. Сделайте чертеж.
8. Докажите, что прямая y = 2x – 1 не пересекает кривую y = x 4 + 3x 2 + 2x. Найдите расстояние между их ближайшими точками.
Ответ:
9. На параболе y = x 2 взяты две точки с абсциссами x1 = 1, x2 = 3. Через эти точки проведена секущая. В какой точке параболы касательная к ней будет параллельна проведенной секущей? Напишите уравнения секущей и касательной.
Ответ: y = 4x – 3 – уравнение секущей; y = 4x – 4 – уравнение касательной.
10. Найдите угол q между касательными к графику функции y = x 3 – 4x 2 + 3x + 1, проведенными в точках с абсциссами 0 и 1.
11. В каких точках касательная к графику функции 
12. В точке A(1; 8) к кривой 
Ответ:
13. Напишите уравнение всех общих касательных к графикам функций y = x 2 – x + 1 и y = 2x 2 – x + 0,5.
Ответ: y = – 3x и y = x.
14. Найдите расстояние между касательными к графику функции 
Ответ:
15. Определите, под какими углами парабола y = x 2 + 2x – 8 пересекает ось абсцисс.
Ответ: q 1 = arctg 6, q 2 = arctg (– 6).
16. На графике функции 
17. Прямая y = 2x + 7 и парабола y = x 2 – 1 пересекаются в точках M и N. Найдите точку K пересечения прямых, касающихся параболы в точках M и N.
18. При каких значениях b прямая y = 9x + b является касательной к графику функции y = x 3 – 3x + 15?
19. При каких значениях k прямая y = kx – 10 имеет только одну общую точку с графиком функции y = 2x 2 + 3x – 2? Для найденных значений k определите координаты точки.
20. При каких значениях b касательная, проведенная к графику функции y = bx 3 – 2x 2 – 4 в точке с абсциссой x0 = 2, проходит через точку M(1; 8)?
21. Парабола с вершиной на оси Ox касается прямой, проходящей через точки A(1; 2) и B(2; 4), в точке B. Найдите уравнение параболы.
Ответ:
22. При каком значении коэффициента k парабола y = x 2 + kx + 1 касается оси Ox?
23. Найдите углы между прямой y = x + 2 и кривой y = 2x 2 + 4x – 3.
Ответ:
24. Определите, под какими углами пересекаются графики функций y = 2x 2 + 3x – 3 и y = x 2 + 2x + 3.
Ответ:
25. При каком значении k угол между кривыми y = x 2 + 2x + k и y = x 2 + 4x + 4 будет равен 45°?
26. Найдите все значения x0, при каждом из которых касательные к графикам функции y = 5cos 3x + 2 и y = 3cos 5x в точках в абсциссой x0 параллельны.
Ответ:
27. Под каким углом видна окружность x 2 + y 2 = 16 из точки (8; 0)?
Ответ:
28. Найдите геометрическое место точек, из которых парабола y = x 2 видна под прямым углом?
Ответ: прямая
29. Найдите расстояние между касательными к графику функции 
Ответ:
30. Найдите геометрическое место вершин всех парабол вида y = x 2 + ax + b, касающихся прямой y = 4x – 1.
Ответ: прямая y = 4x + 3.
Литература
1. Звавич Л.И., Шляпочник Л.Я., Чинкина М.В. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. – М., Дрофа, 1999.
2. Мордкович А. Семинар четвертый для молодых учителей. Тема «Приложения производной». – М., «Математика», № 21/94.
3. Формирование знаний и умений на основе теории поэтапного усвоения умственных действий. / Под ред. П.Я. Гальперина, Н.Ф. Талызиной. – М., МГУ, 1968.


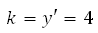
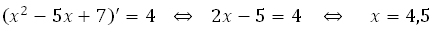
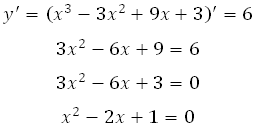
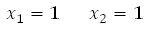




 – абсцисса второй точки касания.
– абсцисса второй точки касания. 


 – уравнение второй касательной.
– уравнение второй касательной.

















