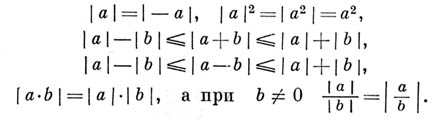Что такое абсолютное значение в алгебре

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

Модуль числа

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

Решим неравенство: |a + 7|

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Источник

СОДЕРЖАНИЕ

Терминология и обозначения

Определение и свойства

Действительные числа

Поскольку символ квадратного корня представляет собой уникальный положительный квадратный корень (в применении к положительному числу), отсюда следует, что

| Икс | знак равно Икс 2 <\ Displaystyle | х | = <\ sqrt <х ^ <2>>>>

эквивалентно определению, приведенному выше, и может использоваться как альтернативное определение абсолютного значения действительных чисел.

Ниже приведены некоторые дополнительные полезные свойства. Это либо непосредственные следствия определения, либо подразумеваются четырьмя фундаментальными свойствами, указанными выше.

Два других полезных свойства, касающихся неравенств:

Эти отношения могут использоваться для решения неравенств, связанных с абсолютными величинами. Например:

Абсолютное значение, как «расстояние от нуля», используется для определения абсолютной разницы между произвольными действительными числами, стандартной метрики действительных чисел.

Сложные числа

где х и у являются действительными числами, то абсолютное значение или модуль из г обозначается | z | и определяется

Когда комплексное число z выражается в полярной форме как

Комплексное абсолютное значение разделяет четыре основных свойства, приведенных выше для реального абсолютного значения.

Важно отметить, что свойство субаддитивности (« неравенство треугольника ») распространяется на любой конечный набор из n комплексных чисел как ( z k ) k знак равно 1 п <\ textstyle (z_ ) _ ^ >

Доказательство комплексного неравенства треугольника

Функция абсолютного значения

Связь со знаковой функцией

Функция абсолютного значения действительного числа возвращает его значение независимо от его знака, тогда как функция знака (или знака) возвращает знак числа независимо от его значения. Следующие уравнения показывают взаимосвязь между этими двумя функциями:

Производная

Реальная функция абсолютного значения является примером непрерывной функции, которая достигает глобального минимума там, где производная не существует.

Первообразный

Первообразной (неопределенного интеграла) вещественной функции абсолютного значения

Расстояние

Стандартное евклидово расстояние между двумя точками

Это можно рассматривать как обобщение, поскольку для и реального, то есть в 1-пространстве, согласно альтернативному определению абсолютного значения, а 1 <\ displaystyle a_ <1>> б 1 <\ displaystyle b_ <1>>

Выше показано, что расстояние «абсолютное значение» для действительных и комплексных чисел согласуется со стандартным евклидовым расстоянием, которое они наследуют в результате рассмотрения их как одномерного и двумерного евклидова пространства соответственно.

Свойства абсолютного значения разности двух действительных или комплексных чисел: неотрицательность, тождество неразличимых, симметрия и неравенство треугольника, данные выше, можно рассматривать как мотивирующие более общее понятие функции расстояния следующим образом:

Обобщения

Заказанные кольца

Четыре основных свойства абсолютного значения для действительных чисел могут быть использованы для обобщения понятия абсолютного значения на произвольное поле следующим образом.

Векторные пространства

Опять же, фундаментальные свойства абсолютного значения для действительных чисел могут быть использованы, с небольшими изменениями, для обобщения этого понятия на произвольное векторное пространство.

Композиционные алгебры

Источник

Что такое модуль числа в математике

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.

Графически абсолютное значение а обозначается как |a|.

Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.

Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Геометрическое значение

Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

Графически это можно выразить следующим образом: |a| = OA.

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.

К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.

|А + 5| = А + 5, если, А больше или равняется нулю.

5-А, если, А значение меньше нуля.

В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.

Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.

Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.

Источник

АБСОЛЮТНАЯ ВЕЛИЧИНА

Об обобщении понятия А. в. на случай произвольного тела см. статью Абсолютное значение.

Смотреть что такое «АБСОЛЮТНАЯ ВЕЛИЧИНА» в других словарях:

АБСОЛЮТНАЯ ВЕЛИЧИНА — величина, рассматриваемая сама по себе, без сравнения с другими. Так, вес данного тела, напр. куска меди, равный положим 3 фунт., есть его абсолютный в., тогда как вес тела сравнительно с весом такого же объема воды относительный или удельный в.… … Словарь иностранных слов русского языка

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа a неотрицательное число (обозначается … Большой Энциклопедический словарь

АБСОЛЮТНАЯ ВЕЛИЧИНА — англ. value of a number, absolute (modul); нем. Grosse der Zahl Absolute. А. в. положительного числа есть само это число; А. в. отрицательного числа есть противоположное ему положительное число; А. в. нуля равна нулю. А. в. числа а обознач./а/.… … Энциклопедия социологии

абсолютная величина — (модуль) действительного числа а, неотрицательное число (обозначается |а|), определяемое так: если а≥0, то |а| = а, если а … Энциклопедический словарь

Абсолютная величина — График вещественной функции … Википедия

абсолютная величина — absoliutusis dydis statusas T sritis automatika atitikmenys: angl. absolute magnitude; absolute quantity vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Automatikos terminų žodynas

абсолютная величина — absoliutusis dydis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, gaunamas statistiniu stebėjimu. atitikmenys: angl. absolute values vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Абсолютная величина — действительного числа равна этому числу, если оно положительно, равна противоположному числу, если оно отрицательно, и равна нулю, если число равно нулю. А. в. числа а обозначается | a |. Например, | +5 | = | 5 | = 5; | 0 |= 0. А. в. (или … Большая советская энциклопедия

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а неотрицат. число (обозначается |а|), определяемое так: если а >= 0, то |а|=а, если а Большой энциклопедический политехнический словарь

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а, неотрицательное число (обозначается |а.|), определяемое так: если а>0, то |а| =а, если a Естествознание. Энциклопедический словарь

Источник