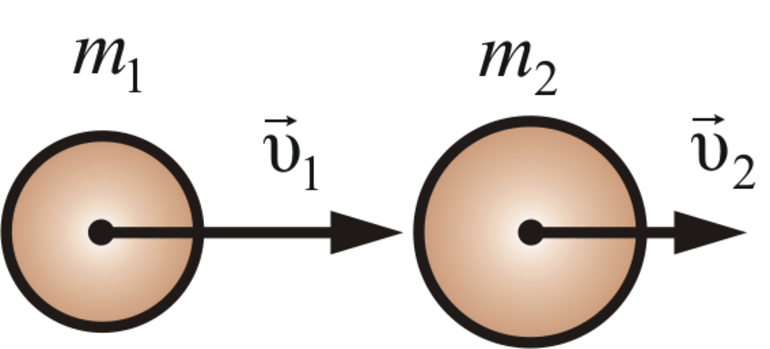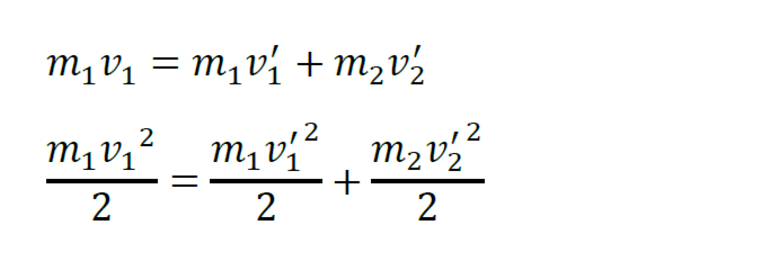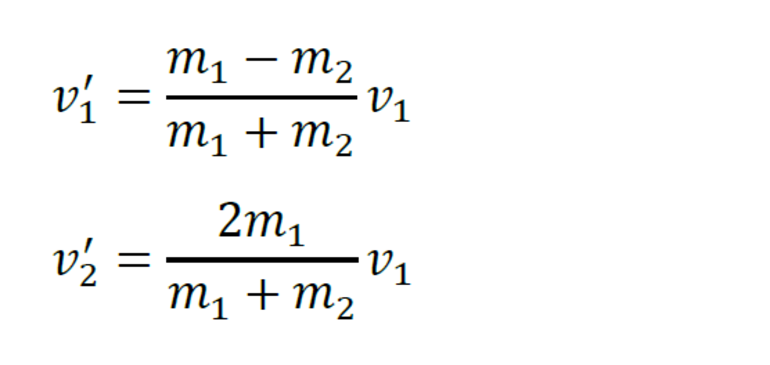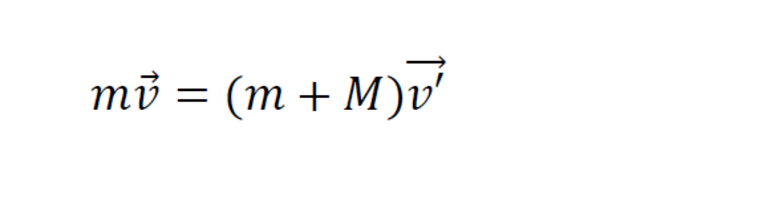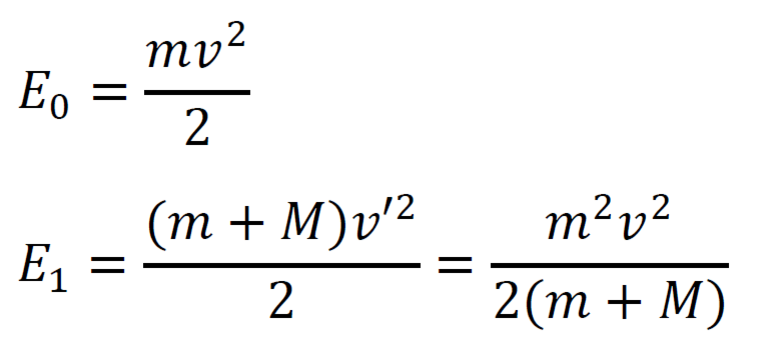Что такое абсолютное упругое столкновение

Что такое абсолютное упругое столкновение

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

Ударом (или столкновением ) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

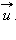
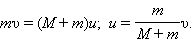Обозначим скорость ящика с застрявшей в нем пулей через Тогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

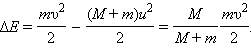Отношение – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

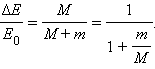Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

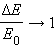
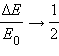
При почти вся кинетическая энергия пули переходит во внутреннюю энергию. При – во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы () отношение

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:

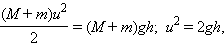где – максимальная высота подъема маятника. Из этих соотношений следует:

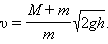Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

В общем случае массы и соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии

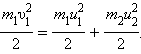Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости и шаров после столкновения:

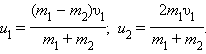Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

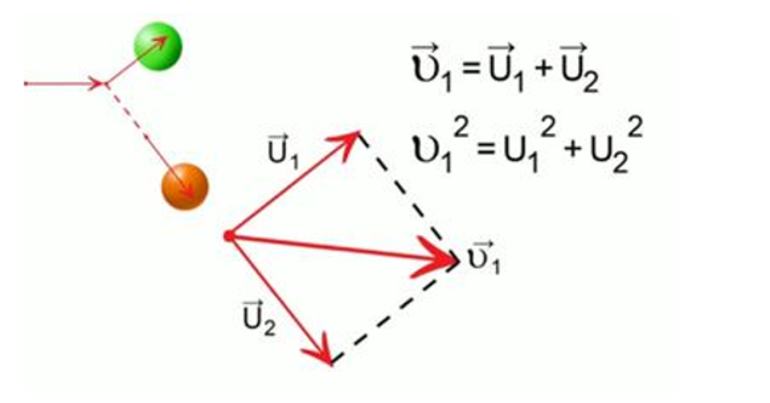
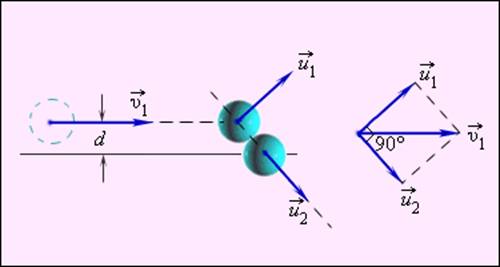
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

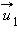
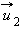
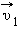
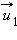
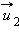
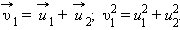После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и после удара нужно знать положение линии центров в момент удара или прицельное расстояние (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При эти законы принимают вид:

Источник

Абсолютно упругий и абсолютно неупругий удар

Механическое взаимодействие в природе можно условно разделить на ударное и безударное.

Безударное взаимодействие – это притяжение и отталкивание.

Для ударного взаимодействия в задачах механики применяют закон сохранения импульса.

Виды ударов

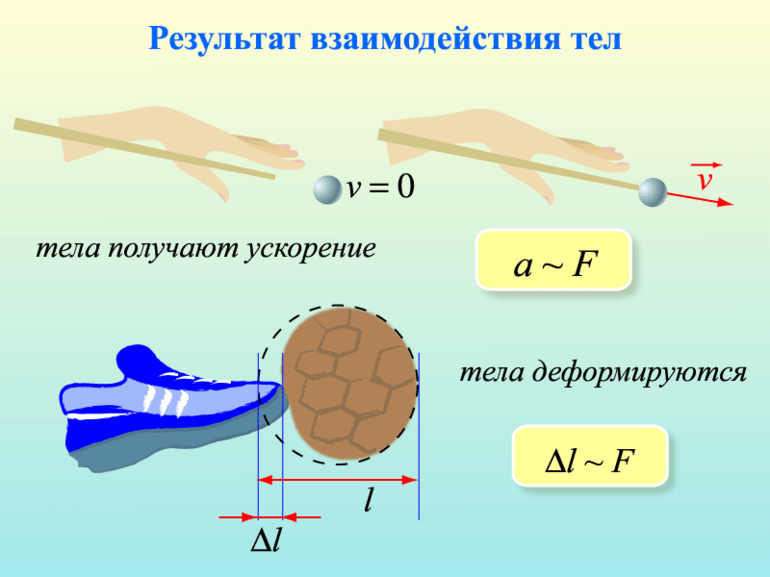
Абсолютно упругий и абсолютно неупругий удары – это два крайних случая на шкале ударного взаимодействия

При ударах большинства реальных тел часть энергии всегда тратится на деформацию этих тел. Поэтому, удары большинства реальных тел лежат на шкале между двумя крайними видами ударов.

Рассмотрим движение тел вдоль одной прямой. Тела либо двигаются навстречу, либо одно тело догоняет другое.

Абсолютно неупругий удар

Суть абсолютно неупругого удара кратко можно описать так: Две капли ртути катились, ударились, слились в общую каплю ртути.

Нарисуем капли ртути до удара. Отметим на рисунке массу каждой капли. Скорости капель укажем с помощью векторов, направленных по движению каждой капли.

Нарисуем ось, для того, чтобы определить знак для импульса каждой капли.

Импульс, сонаправленный с осью, будет иметь положительный знак, направленный против оси – отрицательный.

Сложим векторы импульсов, чтобы найти общий импульс системы – вектор \(\vec>> \).

Каждый импульс запишем со своим знаком

Сделаем второй рисунок, описывающий ситуацию после абсолютно неупругого удара.

Ось поможет выбрать знак для импульса капли.

На рисунке скорость сонаправлена с осью, поэтому, импульс капли после удара имеет положительный знак.

Примечание: Иногда в условии задачи не уточняется, в какую сторону будет двигаться тело после удара. В таком случае, направление движения выбираем сами (влево или вправо на рисунке). Если в ходе решения получим импульс тела, или его скорость со знаком минус, значит, тело движется в противоположную сторону от указанного нами направления. Такой выбор направления ошибкой считаться не будет. А знак минус подскажет, что импульс (и скорость) нужно развернуть в противоположную сторону.

Значит, закон сохранения импульса для абсолютно неупругого удара запишем в таком виде:

При абсолютно неупругом ударе:
— Выполняется закон сохранения импульса,
— Не выполняется закон сохранения энергии, так как часть энергии тратится на деформацию тел.

Примечание: Встречаются задачи вида: человек на льду бросил гирю в горизонтальном направлении, гиря полетела в одну сторону, а человек – в противоположную. Такие задачи решаем, применяя принципы для абсолютно неупругого удара. С той лишь разницей, что меняем местами рисунки до и после удара. Вначале тела находились вместе, после броска – разлетелись в противоположные стороны.

Абсолютно упругий удар

Кратко суть абсолютно упругого удара опишем так: Два бильярдных шара катились, без деформации ударились, и разбежались в разные стороны.

Составим рисунок для ситуации до удара. Отметим на рисунке массу каждого шара. Скорости шаров укажем с помощью векторов, направленных по движению каждого шара.

Запишем импульсы шаров до удара

Нарисуем ось, чтобы определить знаки импульсов каждого шара. Сонаправленный с осью импульс имеет знак «+», направленный против оси – знак «-».

Сложим импульсы и найдем общий импульс системы – вектор \(\vec>> \).

Каждый импульс записываем со своим знаком

На втором рисунке опишем задачу после абсолютно упругого удара.

Укажем массы шаров, их скорости нарисуем стрелками в направлении движения каждого шара. Обозначим скорости символами \(\vec>> \) и \(\vec>> \).

С помощью проведенной оси выбираем знаки импульсов шаров.

Составим выражение для общего импульса после удара.

Для замкнутой системы выполняется закон сохранения импульса

Запишем его в развернутом виде для абсолютно упругого удара:

При абсолютно упругом ударе:
— Выполняется закон сохранения импульса,
— Выполняется закон сохранения энергии.

Алгоритм решения задач на тему закон сохранения импульса

Решение большинства задач на закон сохранения импульса можно проводить по такому алгоритму:

Если тела двигаются под углом друг к другу (вдоль непараллельных прямых)

При решении таких задач, нужно помнить, что, векторы \( \vec>>\) равны. Значит, когда нам известен один из векторов, автоматически становится известен и второй вектор.

Источник

Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

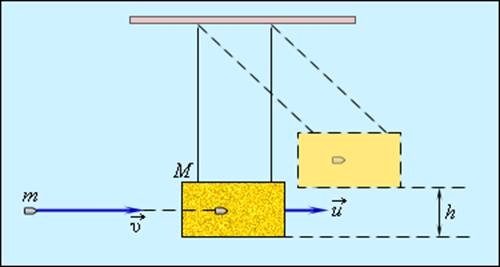
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью 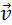попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через 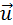Тогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m > М) отношение

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:

где h – максимальная высота подъема маятника. Из этих соотношений следует:

Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

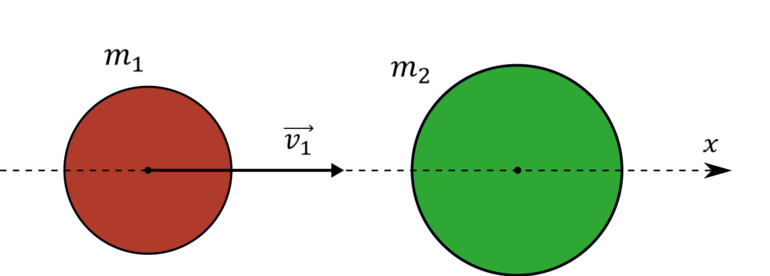
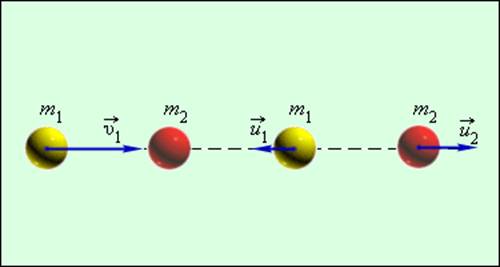
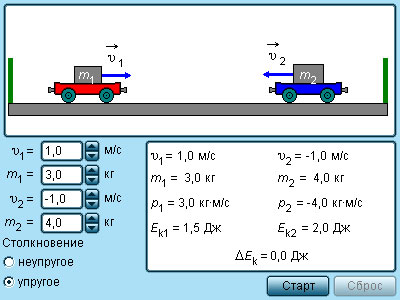
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

В общем случае массы m₁ и m₂ соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии

Здесь υ₁ – скорость первого шара до столкновения, скорость второго шара υ₂ = 0, u₁ и u₂ – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения:

В частном случае, когда оба шара имеют одинаковые массы (m₁ = m₂), первый шар после соударения останавливается (u₁ = 0), а второй движется со скоростью u₂ = υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂ ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂ относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁‘ = υ₁ – υ₂. Определив по приведенным выше формулам скорости u₁ и u₂ шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние

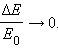
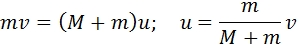
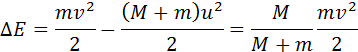
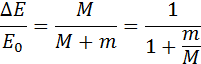
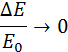
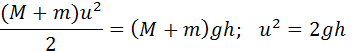
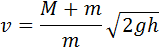
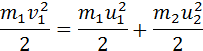
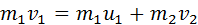
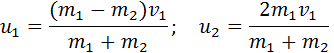
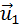После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей и 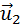после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости 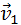налетающего шара. Если массы шаров одинаковы, то векторы скоростей и шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m₁ = m₂ = m эти законы принимают вид:

Первое из этих равенств означает, что векторы скоростей , и образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами и равен 90°.

Источник

Область применения

Столкновения имеют большое значение для изучения вещества. Отражение и рассеяние света, других электромагнитных волн или даже потока электронов могут быть рассмотрены подобно механическим явлениям. На фотографии или рентгеновском снимке можно рассмотреть предметы, не имея возможности сделать это напрямую. Аналогично для исследования устройства микромира физики проводят столкновение ядер свинца в детекторе Большого Адронного Коллайдера.

Сферы использования

Учёные не могут наблюдать столкновение, но датчики фиксируют частицы, которые образуются в его результате, их характеристики (массу, энергию и импульс). Доступная информация очень ограничена, но, проведя длительный анализ полученных данных на основе теории столкновений и множество расчётов, учёные делают удивительные выводы об устройстве нашего мира.

Теоретическая основа

При ударе выполняются законы сохранения импульса и момента импульса. Но механическая энергия, как правило, не сохраняется. Она переходит в нагрев, деформацию тел, колебания (в том числе акустические) и другие виды энергии. Но для удобства рассмотрения в физике применяются упрощённые модели. Поэтому используются предельные случаи:

Абсолютно упругий удар

При абсолютно упругих столкновениях механическая энергия системы тел сохраняется. Интуитивным примером может стать соударение бильярдных шаров или отскакивание теннисного мячика от твёрдой поверхности. Столкновения молекул, атомов и элементарных частиц в ряде случаев хорошо подчиняются законам протекания упругого удара, хотя они и взаимодействуют лишь посредством полей, в первую очередь электромагнитных.

Физическая модель

Если взглянуть поближе, то при столкновении тел происходит их небольшая деформация. Её отчётливо можно заметить для теннисного мячика. Для бильярдного шара она очень мала, а в случае с заряженными частицами изменяет свою форму их электрическое поле. Эти случаи объединяет то, что деформация близка к упругой.

Поверхности сжимаются подобно пружинам, запасая энергию на доли секунды. Кинетическая энергия тел переходит в потенциальную энергию упругой деформации. Но потом поверхности снова выпрямляются, отталкивая тела. В результате энергия снова перетекает в кинетическую. Но эти переходы считаются моментальными. Однако, нельзя считать, что энергия сохранилась для каждого тела. Объекты взаимодействуют и совершают работу. Шар, налетев на другой, теряет скорость. Закон сохранения энергии выполняется лишь для системы, которая не получает приращения энергии от тел извне – закрытой системы.

Тем не менее, кинетическая энергия может быть заключена в разных формах движения тела. Нельзя, например, опрометчиво исключать возможность вращения тел и их форму. Но, опять же, в ряде случаев такими свойствами можно пренебречь. Так работает описание разряженного одноатомного газа (атомы, которые перемещаются по сосуду, взаимодействуя лишь упруго с другими атомами и стенками сосуда).

В ряде случаев удобной для применения является модель центрального удара. В этом случае принимается, что тела движутся только вдоль прямой, проходящей через их центры масс. Таким образом, можно рассматривать только одну координату, разместив ось вдоль этой прямой. В первую очередь для изучения физики процесса используется именно эта ситуация ввиду её простоты. В более общем случае тела могут двигаться к месту столкновения под разными углами и сталкиваться не на одной линии с направлением скорости, однако это существенно усложняет математическую модель.

Пусть один шар покоится, а второй налетает на него с некоторой скоростью, направление которой проходит через центр масс второго шара.

Взаимодействие будем считать центральным и абсолютно упругим ударом, формулы для законов сохранения энергии и импульса будут иметь вид:

При решении этой системы уравнений получаются выражения для скоростей шаров после столкновения:

Можно заметить, что скорость первого может принимать значения обеих знаков. В данном случае рассматриваются проекции скоростей на ось х, поэтому отрицательная скорость означает направление движения против направления оси, т.е. влево. В то же время скорость второго шара имеет лишь положительные значения. Это подтверждает интуитивное предположение о том, что неподвижный шар при таких условиях может быть оттолкнут первым лишь вправо.

Ещё более упрощённый случай строится, когда массы шаров равны. Тем не менее, он несёт ряд интересных эффектов. Подставив одно значение массы в приведённые выше уравнения, получим:

Выходит, что первый шар полностью останавливается, а второй начинает движение со скоростью, равной начальной скорости первого.

Дело в том, что запасённая потенциальная энергия в равных долях переходит обоим телам (согласно третьему закону Ньютона они отталкиваются с равными силами). Выходит, что первый полностью теряет свою кинетическую энергию, ведь столкновение препятствует его движению. Таким образом, вся энергия переходит второму, который разгоняется в той же мере.

Наглядные эффекты

Упругое столкновение лежит в основе широко распространённой игрушки – маятника Ньютона. Одинаковые стальные шарики подвешиваются на тонких нитках так, что они располагаются очень близко, но в то же время не давят друг на друга, а также исключаются их боковые смещения. Если оттянуть и отпустить один – то происходит ряд упругих столкновений. Дело в том, что между шариками в любом случае имеются хоть небольшие зазоры, ведь это не единое тело.

Абсолютно неупругий удар

При абсолютно неупругом столкновении тела соединяются и продолжают движение как единое целое. Импульс сохраняется, а вот часть энергии расходуется и уже не переходит обратно в кинетическую энергию движения этих тел. Два кусочка мягкого пластилина, налетев друг на друга, склеятся и полетят вместе дальше. Но речь может идти и о захвате одного объекта другим. Даже состыковку блоков космической станции можно рассматривать как неупругое столкновение.

Силы, действие которых приводит к убыванию механической энергии системы, называются диссипативными. В первую очередь к диссипативным относятся силы трения и сопротивления среды. Они всегда направлены против движения тела. В технике диссипативные силы очень часто представляют собой существенную проблему. Во-первых, они снижают коэффициент полезного действия устройств. Во-вторых, энергия, переходящая в деформации, акустические волны и выделение тепла несут разрушающее действие. Таким образом, во многих ситуациях инженеры пытаются снизить их действие. Как следствие, учёт вклада неупругих столкновений важен.

Баллистический маятник

Стоит заметить, что формулировки «тонкий», «длинные» несут весьма конкретный смысл. Слово «тонкий» показывает, что влиянием толщины, трения и напряжения в точках крепления можно пренебречь. «Длинные» нити – смещением по вертикали можно пренебречь. Хотя время удара пули настолько мало, что отклонением можно пренебречь вне зависимости от длины нити.

До столкновения ящик неподвижен, учитывается только энергия пули. После – энергия ящика и пули как единого целого. Начальная и конечная кинетические энергии:

Их разность и покажет потери механической энергии:

Потери кинетической энергии не пропадают бесследно, они переходят в нагрев пули и песка, а также образование акустических волн.

Частные случаи

Важные выводы можно сделать, проверив полученные выражения при различных соотношениях масс ящика и пули. При равных массах уйдёт половина энергии. Если масса пули значительно меньше массы ящика – рассеется почти вся. Когда намного больше – потеряется малая часть, массивное подвижное тело будто бы и не заметит мелкого препятствия.

Реальный удар

В реальных условиях столкновения крайне редко являются такими, что их можно считать абсолютно упругими или неупругими. Они находятся где-то между предельными случаями, поэтому рассматриваются как комбинация этих процессов.

Коэффициент восстановления

Вводится коэффициент восстановления, который показывает степень близости к абсолютно упругому удару:

Значения для некоторых материалов

Приведем величины для различных сталкивающихся веществ:

Коэффициент восстановления показывает, какая доля начальной относительной скорости этих тел восстанавливается к концу удара.

Если предположить, что тело ударяется о неподвижную преграду (или тело гораздо большей массы), то коэффициент покажет соотношение между скоростями первого тела до и после столкновения.

Источник

• ← Что такое абсолютное умение в валоран
• Что такое абсолютное число →