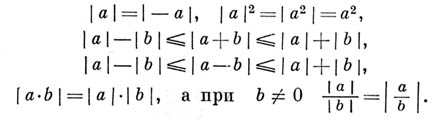Что такое абсолютное число

Абсолютные и относительные статистические величины

Понятие абсолютных величин

Абсолютные величины — это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.

Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).

Единицы измерения абсолютных величин могут быть 3 видов:

Абсолютные величины могут быть моментными или интервальными. Моментные абсолютные величины показывают уровень изучаемого явления или процесса на определенный момент времени или дату (например, количество денег в кармане или стоимость основных фондов на первое число месяца). Интервальные абсолютные величины — это итоговый накопленный результат за определенный период (интервал) времени (например, зарплата за месяц, квартал или год). Интервальные абсолютные величины, в отличие от моментных, допускают последующее суммирование.

Абсолютная статистическая величина обозначается X, а их общее число в статистической совокупности — N.

Количество величин с одинаковым значением признака обозначается f и называется частота (повторяемость, встречаемость).

Cами по себе абсолютные статистические величины не дают полного представления об изучаемом явлении, так как не показывают его динамику, структуру, соотношение между частями. Для этих целей служат относительные статистические величины.

Понятие и виды относительных величин

Относительная статистическая величина — это результат соотношения двух абсолютных статистических величин.

Если соотносятся абсолютные величины с одинаковой размерностью, то получаемая относительная величина будет безразмерной (размерность сократится) и носит название коэффициент.

Часто применяется искусственная размерность коэффициентов. Она получается путем их умножения:

Искусственная размерность коэффициентов применяется, как правило, в разговорной речи и при формулировании результатов, а в самих расчетах она не используется. Чаще всего применяются проценты, в которых принято выражать полученные значения относительных величин.

Чаще вместо названия относительная статистическая величина используется более краткий термин-синоним — индекс (от лат. index — показатель, коэффициент).

В зависимости от видов соотносимых абсолютных величин при расчете относительных величин, получаются разные виды индексов: динамики, планового задания, выполнения плана, структуры, координации, сравнения, интенсивности.

Индекс динамики

Индекс динамики (коэффициент роста, темп роста) показывает во сколько раз изменилось изучаемое явление или процесс во времени. Рассчитывается как отношение значения абсолютной величины в отчетный (анализируемый) период или момент времени к базисному (предыдущему):

.

Здесь и далее подиндексы означают: 1 — отчетный (анализируемый) период, 0 — базисный (прошлый) период.

Индекс планового задания

Индекс планового задания – это отношение планового значения абсолютной величины к базисному:

Например, автосалон в январе продал 100 автомобилей, а на февраль запланировал продать 120 автомобилей. Тогда индекс планового задания составит i пз = 120/100 = 1,2, что означает планирование роста продаж в 1,2 раза или на 20%

Индекс выполнения плана

Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:

Например, автосалон в феврале продал 110 автомобилей, хотя на февраль было запланировано продать 120 автомобилей. Тогда индекс выполнения плана составит i вп = 110/120 = 0,917, что означает выполнение плана на 91,7%, то есть план недовыполнен на (100%-91,7%) = 8,3%.

Перемножая индексы планового задания и выполнения плана, получим индекс динамики:

В рассмотренном ранее примере про автосалон, если перемножим полученные значения индексов планового задания и выполнения плана, то получим значение индекса динамики: 1,2*0,917 = 1,1.

Индекс структуры

Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.

Например, если в рассматриваемой группе студентов 20 девушек и 10 молодых людей, тогда индекс стурктуры (доля) девушек будет равен 20/(20+10) = 0,667, то есть доля девушек в группе составляет 66,7%.

Индекс координации

Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.

Например, если в группе студентов из 20 девушек и 10 молодых людей, принять за базу сравнения численность девушек, тогда индекс координации численности молодых людей составит 10/20 = 0,5, то есть численность молодых людей составляет 50% от численности девушек в группе.

Индекс сравнения

где А, Б — признаки сравниваемых объектов или территорий.

Индекс интенсивности

Например, хлебный магазин продал 500 буханок хлеба и заработал на этом 10000 руб., тогда индекс интенсивности составит 10000/500 = 20 [руб./бух.хлеба], то есть цена продажи хлеба составила 20 руб. за буханку.

Большинство величин с дробной размерностью представляют собой индексы интенсивности.

Источник

АБСОЛЮТНАЯ ВЕЛИЧИНА

Об обобщении понятия А. в. на случай произвольного тела см. статью Абсолютное значение.

Смотреть что такое «АБСОЛЮТНАЯ ВЕЛИЧИНА» в других словарях:

АБСОЛЮТНАЯ ВЕЛИЧИНА — величина, рассматриваемая сама по себе, без сравнения с другими. Так, вес данного тела, напр. куска меди, равный положим 3 фунт., есть его абсолютный в., тогда как вес тела сравнительно с весом такого же объема воды относительный или удельный в.… … Словарь иностранных слов русского языка

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа a неотрицательное число (обозначается … Большой Энциклопедический словарь

АБСОЛЮТНАЯ ВЕЛИЧИНА — англ. value of a number, absolute (modul); нем. Grosse der Zahl Absolute. А. в. положительного числа есть само это число; А. в. отрицательного числа есть противоположное ему положительное число; А. в. нуля равна нулю. А. в. числа а обознач./а/.… … Энциклопедия социологии

абсолютная величина — (модуль) действительного числа а, неотрицательное число (обозначается |а|), определяемое так: если а≥0, то |а| = а, если а … Энциклопедический словарь

Абсолютная величина — График вещественной функции … Википедия

абсолютная величина — absoliutusis dydis statusas T sritis automatika atitikmenys: angl. absolute magnitude; absolute quantity vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Automatikos terminų žodynas

абсолютная величина — absoliutusis dydis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, gaunamas statistiniu stebėjimu. atitikmenys: angl. absolute values vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Абсолютная величина — действительного числа равна этому числу, если оно положительно, равна противоположному числу, если оно отрицательно, и равна нулю, если число равно нулю. А. в. числа а обозначается | a |. Например, | +5 | = | 5 | = 5; | 0 |= 0. А. в. (или … Большая советская энциклопедия

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а неотрицат. число (обозначается |а|), определяемое так: если а >= 0, то |а|=а, если а Большой энциклопедический политехнический словарь

АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а, неотрицательное число (обозначается |а.|), определяемое так: если а>0, то |а| =а, если a Естествознание. Энциклопедический словарь

Источник

Абсолютная величина. Модуль.

Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).

Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.

Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:

Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:

Абсолютные величины, виды:

Свойства модуля.

.

Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.

Основные свойства абсолютной величины.

Вещественные числа.

Комплексные числа.

Алгебраические свойства абсолютной величины.

Для каждого имеют место следующие соотношения:

Как для вещественных, так и для комплексных a, b имеют место соотношения:

Источник

Существует ли в естественных и гуманитарных науках, абсолютное число?

Отвечу про гуманитарные науки на примерах, по такому же принципу рассчитываются абсолютные величины при каких либо исторических событиях :

Абсолютные величины имеют большое научное и практичес­кое значение. По ним можно судить о размерах преступных прояв­лений, численности осужденных, количестве рассмотренных граж­данских исков, возмещении причиненного ущерба и других собы­тиях. Некоторые показатели, выраженные в абсолютных величи­нах, достаточно убедительны. К примеру, в 1960 г. в США было совершено 2 млн «серьезных» преступлений, а в 1990 г. — 14,5 млн. Приведенные данные красноречиво говорят как о высоком уров­не преступности в США, так и о неблагоприятной тенденции ее роста за указанный тридцатилетний период.

Абсолютные показатели являются базовыми. Любые статисти­ческие операции (расчет относительных и средних величин, ин­дексов или коэффициентов, построение статистических рядов или установление корреляций) основываются на абсолютных вели­чинах. Однако их собственные аналитические возможности огра­ничены. По абсолютным сведениям, например, трудно судить об уровне преступности в разных городах или регионах и практи­чески нельзя ответить на вопрос, где преступность выше, а где ниже, так как города или регионы могут существенно различаться по численности населения, территории и другим важным пара­метрам. Одно дело — город со 100-тысячным населением и дру­гое — мегаполис с несколькими миллионами жителей. В после­днем случае число преступлений будет многократно выше, но может быть совсем не настолько, на сколько в нем больше жите­лей. Тогда преступность в малом городе в расчете на население окажется выше, чем в большом.

Точно также по одним абсолютным данным учтенных и рас­крытых преступлений в различных правоохранительных органах (милиции, прокуратуре, налоговой полиции) трудно ответить на вопрос, в каком из этих органов раскрываемость преступлений выше. В 1995 г. в Татарстане было зарегистрировано 59 417 дея­ний, а в Туве — 8377. Различия по безотносительным абсолют­ным показателям семикратные. Если же рассчитать число пре­ступлений на одно и то же число населения, например, на 100 тыс. всех жителей, то в Татарстане этот показатель составит 1580,8, а в Туве — 2724,4, т. е. в 1,7 раза выше, чем в Татарстане.

Если рассчитать тот же показатель и на те же 100 тыс. жителей в возрасте уголовной ответственности, т. е. с 14 лет и старше, то в Туве (где рождаемость выше и доля несовершеннолетних боль­ше) число преступлений на 100 тыс. жителей в возрасте уголов­ной ответственности составит 3990,1, а в Татарстане — 2011,6. По этим показателям преступность в Туве выше, чем в Татарста­не, практически в 2 раза.

Таким образом, использование показателей преступности, соотнесенных с численностью населения, свидетельствует о су­щественной ограниченности аналитических возможностей абсо­лютных величин. Поэтому, если опираться только на них, мож­но прийти к ошибочным выводам. Такие ошибки нередко «до­пускаются» то ли из статистического невежества, то ли из поли­тических спекуляций.

Источник

СОДЕРЖАНИЕ

Терминология и обозначения

Определение и свойства

Действительные числа

Поскольку символ квадратного корня представляет собой уникальный положительный квадратный корень (в применении к положительному числу), отсюда следует, что

| Икс | знак равно Икс 2 <\ Displaystyle | х | = <\ sqrt <х ^ <2>>>>

эквивалентно определению, приведенному выше, и может использоваться как альтернативное определение абсолютного значения действительных чисел.

Ниже приведены некоторые дополнительные полезные свойства. Это либо непосредственные следствия определения, либо подразумеваются четырьмя фундаментальными свойствами, указанными выше.

Два других полезных свойства, касающихся неравенств:

Эти отношения могут использоваться для решения неравенств, связанных с абсолютными величинами. Например:

Абсолютное значение, как «расстояние от нуля», используется для определения абсолютной разницы между произвольными действительными числами, стандартной метрики действительных чисел.

Сложные числа

где х и у являются действительными числами, то абсолютное значение или модуль из г обозначается | z | и определяется

Когда комплексное число z выражается в полярной форме как

Комплексное абсолютное значение разделяет четыре основных свойства, приведенных выше для реального абсолютного значения.

Важно отметить, что свойство субаддитивности (« неравенство треугольника ») распространяется на любой конечный набор из n комплексных чисел как ( z k ) k знак равно 1 п <\ textstyle (z_ ) _ ^ >

Доказательство комплексного неравенства треугольника

Функция абсолютного значения

Связь со знаковой функцией

Функция абсолютного значения действительного числа возвращает его значение независимо от его знака, тогда как функция знака (или знака) возвращает знак числа независимо от его значения. Следующие уравнения показывают взаимосвязь между этими двумя функциями:

Производная

Реальная функция абсолютного значения является примером непрерывной функции, которая достигает глобального минимума там, где производная не существует.

Первообразный

Первообразной (неопределенного интеграла) вещественной функции абсолютного значения

Расстояние

Стандартное евклидово расстояние между двумя точками

Это можно рассматривать как обобщение, поскольку для и реального, то есть в 1-пространстве, согласно альтернативному определению абсолютного значения, а 1 <\ displaystyle a_ <1>> б 1 <\ displaystyle b_ <1>>

Выше показано, что расстояние «абсолютное значение» для действительных и комплексных чисел согласуется со стандартным евклидовым расстоянием, которое они наследуют в результате рассмотрения их как одномерного и двумерного евклидова пространства соответственно.

Свойства абсолютного значения разности двух действительных или комплексных чисел: неотрицательность, тождество неразличимых, симметрия и неравенство треугольника, данные выше, можно рассматривать как мотивирующие более общее понятие функции расстояния следующим образом:

Обобщения

Заказанные кольца

Четыре основных свойства абсолютного значения для действительных чисел могут быть использованы для обобщения понятия абсолютного значения на произвольное поле следующим образом.

Векторные пространства

Опять же, фундаментальные свойства абсолютного значения для действительных чисел могут быть использованы, с небольшими изменениями, для обобщения этого понятия на произвольное векторное пространство.

Композиционные алгебры

Источник