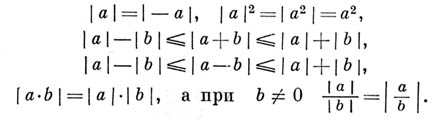Что такое абсолютная величина числа
Модуль числа
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль числа в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
Решим неравенство: |a + 7|
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
Оно равно a при а > 0 и −а, при а
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Абсолютная величина. Модуль.
Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).
Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.
Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:
Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:
Абсолютные величины, виды:
Свойства модуля.
.
Так как частное 
= 
, то 
. В силу предыдущего свойства имеем . Воспользуемся равенством 
, которое справедливо в силу определения модуля числа.
Основные свойства абсолютной величины.
Вещественные числа.
Комплексные числа.
Алгебраические свойства абсолютной величины.
Для каждого 
имеют место следующие соотношения:
Как для вещественных, так и для комплексных a, b имеют место соотношения:
Абсолютная величина. Модуль.
Абсолютными величинами называются — объем или размер события, которое изучается или явления, процесса, который выражен в соответствующих единицах измерения в конкретных условиях места и времени.Или, другими словами: это просто число без учёта знака (всегда с плюсом).
Абсолютная величина числа или модуль числа x — неотрицательное число, определение которого зависит от типа числа x. Обозначается: |x|.
Если x вещественный, то абсолютная величина – это непрерывная кусочно-линейная функция, которая определяется так, формула:
Обобщением этого понятия есть модуль комплексного числа z=x+iy, иногда называют абсолютной величиной. Его определяют формулой:
Абсолютные величины, виды:
Свойства модуля.
.
Так как частное = , то . В силу предыдущего свойства имеем . Воспользуемся равенством , которое справедливо в силу определения модуля числа.
Основные свойства абсолютной величины.
Вещественные числа.
Комплексные числа.
Алгебраические свойства абсолютной величины.
Для каждого имеют место следующие соотношения:
Как для вещественных, так и для комплексных a, b имеют место соотношения:
АБСОЛЮТНАЯ ВЕЛИЧИНА
Об обобщении понятия А. в. на случай произвольного тела см. статью Абсолютное значение.
Смотреть что такое «АБСОЛЮТНАЯ ВЕЛИЧИНА» в других словарях:
АБСОЛЮТНАЯ ВЕЛИЧИНА — величина, рассматриваемая сама по себе, без сравнения с другими. Так, вес данного тела, напр. куска меди, равный положим 3 фунт., есть его абсолютный в., тогда как вес тела сравнительно с весом такого же объема воды относительный или удельный в.… … Словарь иностранных слов русского языка
АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа a неотрицательное число (обозначается … Большой Энциклопедический словарь
АБСОЛЮТНАЯ ВЕЛИЧИНА — англ. value of a number, absolute (modul); нем. Grosse der Zahl Absolute. А. в. положительного числа есть само это число; А. в. отрицательного числа есть противоположное ему положительное число; А. в. нуля равна нулю. А. в. числа а обознач./а/.… … Энциклопедия социологии
абсолютная величина — (модуль) действительного числа а, неотрицательное число (обозначается |а|), определяемое так: если а≥0, то |а| = а, если а … Энциклопедический словарь
Абсолютная величина — График вещественной функции … Википедия
абсолютная величина — absoliutusis dydis statusas T sritis automatika atitikmenys: angl. absolute magnitude; absolute quantity vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Automatikos terminų žodynas
абсолютная величина — absoliutusis dydis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, gaunamas statistiniu stebėjimu. atitikmenys: angl. absolute values vok. absolute Größe, f rus. абсолютная величина, f pranc. grandeur absolue, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Абсолютная величина — действительного числа равна этому числу, если оно положительно, равна противоположному числу, если оно отрицательно, и равна нулю, если число равно нулю. А. в. числа а обозначается | a |. Например, | +5 | = | 5 | = 5; | 0 |= 0. А. в. (или … Большая советская энциклопедия
АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а неотрицат. число (обозначается |а|), определяемое так: если а >= 0, то |а|=а, если а Большой энциклопедический политехнический словарь
АБСОЛЮТНАЯ ВЕЛИЧИНА — (модуль) действительного числа а, неотрицательное число (обозначается |а.|), определяемое так: если а>0, то |а| =а, если a Естествознание. Энциклопедический словарь