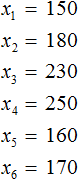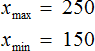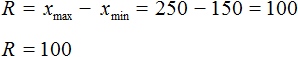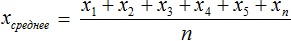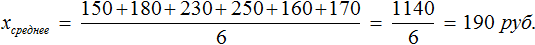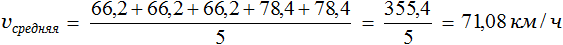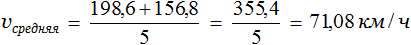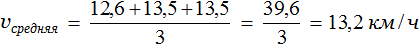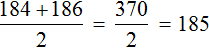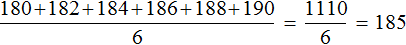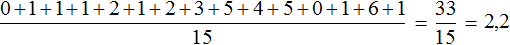Что такое абсолютная частота в алгебре
Курс алгебры в 7-м классе «Относительная частота случайного события»
Разделы: Математика
Оборудование: компьютер, проектор, экран.
I. Самоопределение к учебной деятельности
— На прошлом уроке вы получили задание подготовить сообщение по теме «Что такое теория вероятностей». Давайте заслушаем сообщение.
«Что такое теория вероятностей»
В повседневной жизни в разговоре часто используется слово «вероятность», например: «это невероятный случай», «вероятнее всего он опоздает» и т.д. Здесь интуитивно оценивается возможность того или иного события, исходя из здравого смысла, интуиции. Например, мы заранее знаем, что на детский сеанс пойдет больше школьников, чем взрослых, или, что при выполнении многих видов работ вредна торопливость, т.к. в спешке можно сделать брак.
В задачах, которые мы решаем на уроках математики у всех получается один и тот же ответ. И этот ответ не зависит от способа решения задачи, а зависит только от правильности выполнения вычислений. В реальной же жизни не все так просто. Многие события нельзя предсказать заранее. Мы не можем знать, какая погода будет в первый день весны, когда будет первая гроза. Нельзя наверняка сказать, сколько человек решат позвонить по телефону в ближайший час. Кто может гарантировать, что если я сейчас пойду в магазин, то обязательно встречу там свою одноклассницу. Все эти события могут произойти, а могут не и не произойти. Поэтому эти события называются случайными.
Оказывается, что случайные события тоже имеют свои закономерности, которые изучает раздел математики – Теория вероятностей.
Теория вероятностей неразрывно связана с нашей повседневной жизнью. Она помогает оценить свои шансы на успех, принимать оптимальные решения.
— Сегодня мы начинаем знакомство с очень интересным разделом математики – теорией вероятностей.
1. Устная работа (задания проецируются на экран)
1. Что называется отношением двух чисел? (Отношением двух чисел называется их частное).
2. Найдите отношение чисел:
а) 4 к 8; б) 2 к 
Ответ: а) 0,5; б) 3; в) 4.
3. Из 25 студентов группы 7 отличников. Какой процент всех студентов группы составляют отличники?
4. Из 2000 зерен гороха 1800 оказались всхожими. Определите процент всхожести зерен.
5. Определите процент содержания соли в растворе, если в 300 г раствора содержится 15 г соли.
2. Индивидуальное задание:
За четверть домашнее задание по алгебре было задано 16 раз.
а) Света два раза не сделала домашнее задание. Какова частота невыполнения домашнего задания у Светы за четверть?
б) Женя не сделал домашнее задание девять раз. Какова частота выполнения домашнего задания у Жени за четверть?
III. Выявление причины затруднения и постановка цели деятельности
— В чем причина затруднения? (Не знаем, как определить частоту события).
— Какова цель урока? (Научиться находить частоту события).
— Запишите тему урока: «Относительная частота случайного события».
IV. Изучение нового материала
1. Теоретический материал.
Частота случайного события
Теория вероятностей имеет дело с экспериментами, исходы которых непредсказуемы: они зависят от случая. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно вычислить, как часто оно происходит. Для этого используют важные величины: абсолютную и относительную частоту.
Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие.
Относительная частота показывает, какая доля экспериментов завершилась наступлением данного исхода.
Определение. Относительной частотой события А называют отношение абсолютной частоты 
Поскольку 0 ≤ 
При определении относительной частоты случайного события результаты удобно сводить в таблицу.
2. Практическая часть
1) Проведем лабораторную работу (работа в группах по 2 человека.)
Цель работы: определить абсолютную и относительную частоту каждого исхода; выяснить, чему равна сумма абсолютных частот и сумма относительных частот.
Оборудование: игральные кубики, пластмассовые стаканчики.
1. Провести 50 экспериментов по выбрасыванию игрального кубика из закрытого сосуда – стаканчика.
2. Полученные результаты оформить в виде таблицы.
3. Найдите абсолютную и относительную частоты для каждого исхода.
4. Подсчитайте, чему равна сумма абсолютных частот и чему равна сумма относительных частот.
Протокол экспериментального исследования частоты выпадения различных очков игрального кубика.
Частота абсолютная и относительная. Статистическое определение вероятности
Теория вероятностей имеет дело с испытаниями, исходы которых непредсказуемы: они зависят от случая. О таких испытаниях мы уже говорили – это подбрасывание монеты и кубика, проверка лотерейных билетов, падение бутерброда на пол и т.д.
Для всех таких испытаний характерно то, что их можно многократно повторять (хотя бы мысленно) в одних и тех же условиях. То есть условия проведения испытания не меняются, а результаты могут быть совершенно различными (такие испытания называют массовыми однородными испытаниями).
Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное с испытанием, нужно подсчитать, как часто оно происходит. Для этого используют два важных теоретико-вероятностных понятия.
Определение. Пусть проводится n однородных испытаний. Число испытаний, в которых событие А произошло, называется абсолютной частотой появления события.
Определение. Пусть проводится n однородных испытаний, и пусть событие А произошло в m из них. Число равное отношению числа всех проведенных испытаний к числу испытаний, в которых событие А произошло, называется относительной частотой появления события А.
Относительная частота появления события А обозначается: W(А). Таким образом, по определению, 
Замечание. Относительную частоту можно найти, поделив абсолютную частоту на число испытаний. Иногда относительную частоту измеряют в процентах.
Рассмотрим пример: игральный кубик подбросили 50 раз, и исходы испытаний занесли в таблицу, в первом строке которой перечислены все возможные исходы, во второй и третьей строках фиксировались значения абсолютной и относительных частот соответственно
| Исходы | ||||||
| абсолютная частота | ||||||
| относительная частота | 0,18 | 0,12 | 0,16 | 0,22 | 0,18 | 0,14 |
Полученная таблица обладает некоторыми замечательными свойствами, которые характерны для любой таблицы абсолютных и относительных частот:
1) сумма абсолютных частот по всем исходам испытания равна числу проведенных испытаний, для данной таблицы – 50;
2) сумма относительных частот по всем исходам испытания равна 1.
Замечание. Проверка этих свойств поможет в дальнейшем избегать ошибок при заполнении таких таблиц.
Наглядной иллюстрацией распределения абсолютных и относительных частот служат гистограммы, на которых каждая из частот изображается в виде столбика соответствующей высоты. Гистограмма относительных частот для рассмотренного примера изображена на следующем рисунке
По таблице и гистограмме легко оценивать, какой исход в данной серии испытаний появляется чаще остальных. В данном примере видно, что четверка выпадала в этой серии испытаний чаще остальных, а двойка реже. Но можно ли на этом основании сказать, что исход «4» более вероятен, чем исход «2»?
Пусть проводится серия испытаний, и фиксируются абсолютные и относительные частоты исходов испытаний. Выясним, как ведут себя частоты при увеличении числа испытаний в серии. Это удобно наблюдать на конкретном примере.
Пример. Игральный кубик подбрасывали 1000 раз, и после каждой серии из 100 подбрасываний фиксировали относительную частоту появления каждого исхода. В результате была получена следующая таблица.
| Количество испытаний | Частота исходов | ||||
| 0,16 | 0,16 | 0,2 | 0,15 | 0,19 | 0,14 |
| 0,16 | 0,135 | 0,185 | 0,16 | 0,18 | 0,18 |
| 0,167 | 0,16 | 0,163 | 0,153 | 0,183 | 0,173 |
| 0,168 | 0,153 | 0,175 | 0,163 | 0,185 | 0,158 |
| 0,164 | 0,146 | 0,182 | 0,16 | 0,186 | 0,162 |
| 0,152 | 0,157 | 0,183 | 0,153 | 0,188 | 0,167 |
| 0,153 | 0,164 | 0,180 | 0,151 | 0,186 | 0,166 |
| 0,159 | 0,164 | 0,181 | 0,155 | 0,180 | 0,161 |
| 0,156 | 0,164 | 0,183 | 0,166 | 0,171 | 0,160 |
| 0,158 | 0,170 | 0,182 | 0,165 | 0,168 | 0,157 |
Построим график зависимости, например частоты выпадения тройки, от числа экспериментов.
По графику видно, что относительная частота появления тройки вначале проведения серии испытаний испытывает значительные колебания, но с ростом числа испытаний она стабилизируется около значения 0,18. Построив графики зависимостей относительных частот появления других исходов, от числа проведенных испытаний можно убедиться в аналогичном результате. Поэтому, можно сделать вывод, что относительная частота появления той или другой цифры, в данном случае, стабилизируется с ростом числа испытаний.
Оказывается, что такое свойство относительных частот имеет место и в общем случае. Говорят, что с ростом числа однородных испытаний относительная частота появления события приобретает свойство устойчивости, мало отличается от некоторого фиксированного числа. На этом факте основывается одно из определений вероятности.
Определение. Статистической вероятностью события А называется число вокруг которого колеблется относительная частота появления события А в длинной серии испытаний.
Замечание. Следует заметить, что данное определение не является математически строгим, оно скорее, экспериментальное.
Абсолютная частота
Опубликовано 29.05.2021 · Обновлено 29.05.2021
Что такое абсолютная частота?
Абсолютная частота – это статистический термин, описывающий, сколько раз конкретная часть данных или конкретное значение появляется во время испытания или набора испытаний. По сути, абсолютная частота – это простой подсчет количества наблюдений за значением. Абсолютная частота обычно выражается целым числом и считается базовым уровнем статистического анализа.
Понимание абсолютной частоты
Абсолютная частота часто является компонентом сбора основных данных. Например, если вы спросите 10 друзей, является ли синий их любимый цвет, и трое скажут «да», а семь – нет, у вас будет достаточно информации, чтобы определить абсолютную частоту: абсолютная частота «да» равна трем, а частота «нет» равна равно семи. Количество отслеживаемых значений часто увеличивается с увеличением размера выборки или объема исследования. Например, если вы спросите 100 человек, является ли их любимый цвет синим, абсолютная частота, скорее всего, увеличится. Однако нет никакой дополнительной сложности в отслеживании того, сколько раз встречается данное значение.
В некоторых визуализациях данных используется абсолютная частота. Например, абсолютная частота ответов на опрос часто отображается на графике, чтобы обеспечить удобное представление большинства ответов на конкретный вопрос.
Абсолютная частота может использоваться для отображения наиболее часто встречающихся данных в испытании или исследовании, но обычно не используется в качестве первичного статистического измерения.
Ключевые выводы
Абсолютная частота против относительной частоты
Абсолютная частота может быть отправной точкой для более детального статистического анализа. Относительная частота, например, получается из абсолютной частоты. Когда абсолютная частота значений отслеживается на протяжении всего испытания, абсолютная частота для конкретного значения затем может быть разделена на общее количество значений для этой переменной на протяжении всего испытания, чтобы получить относительную частоту. Мы чаще всего ссылаемся на относительную частоту, будь то процент побед нашей любимой спортивной команды или процент управляющих фондами, опередивших рынок. В отличие от абсолютной частоты, относительная частота обычно выражается в процентах или дробях, а не целым числом.
Иногда, когда относительные частоты очень малы, они даются в единицах «на тысячу», «на миллион» и т. Д., Как общее количество преступлений в городе на тысячу человек. Такие корректировки называются «на душу населения».
Пример абсолютной частоты
Представьте себе конференцию по бухгалтерскому учету, которая хочет собрать данные о привычках к употреблению алкоголя в профессии. Организатор конференции спрашивает у комнаты из 50 бухгалтеров, сколько бокалов вина они выпили за последнюю неделю. После того, как каждый из 50 бухгалтеров дает свой ответ, он помещается в таблицу с абсолютными частотами.
Есть несколько наблюдений, которые вы можете сделать из таблицы, отображающей абсолютную частоту: большее количество бухгалтеров пьют некоторое количество алкоголя, чем не употребляют алкоголь. Однако наиболее ценные наблюдения, которые можно сделать из этого набора данных, требуют дополнительного анализа. Например, 50% бухгалтеров на конференции выпивают пять и более напитков в неделю.
Однако как статистическое исследование этот обзор оставляет желать лучшего. Во-первых, нет демографической информации, кроме профессии респондентов. Пол респондентов не разглашается. Это важно, поскольку существуют разные рекомендации по употреблению алкоголя в зависимости от пола. Мы также не знаем крепость или объем алкоголя (ABV) конкретного напитка, о котором сообщают. Как и абсолютная частота, наш пример опроса – это только начало реального анализа потребления алкоголя в бухгалтерской профессии.
Элементы статистики
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
Элементы выборки обозначаются с помощью переменных с индексами 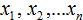
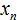
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
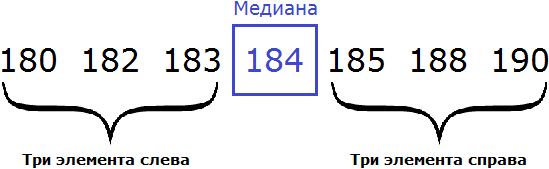
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
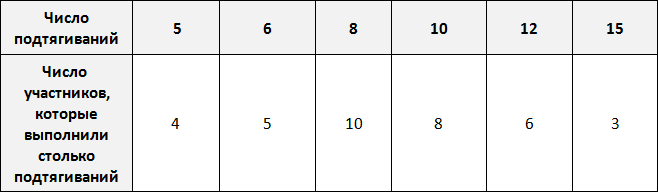
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
42 thoughts on “Элементы статистики”
Спасибо, что вы вернулись.
Будут ли новые уроки?