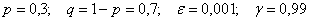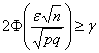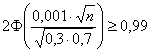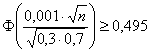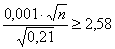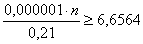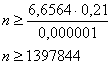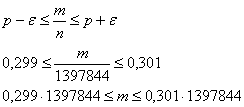Что такое абсолютная частота относительная частота
Частота абсолютная и относительная. Статистическое определение вероятности
Теория вероятностей имеет дело с испытаниями, исходы которых непредсказуемы: они зависят от случая. О таких испытаниях мы уже говорили – это подбрасывание монеты и кубика, проверка лотерейных билетов, падение бутерброда на пол и т.д.
Для всех таких испытаний характерно то, что их можно многократно повторять (хотя бы мысленно) в одних и тех же условиях. То есть условия проведения испытания не меняются, а результаты могут быть совершенно различными (такие испытания называют массовыми однородными испытаниями).
Чтобы выяснить, насколько вероятно то или иное случайное событие, связанное с испытанием, нужно подсчитать, как часто оно происходит. Для этого используют два важных теоретико-вероятностных понятия.
Определение. Пусть проводится n однородных испытаний. Число испытаний, в которых событие А произошло, называется абсолютной частотой появления события.
Определение. Пусть проводится n однородных испытаний, и пусть событие А произошло в m из них. Число равное отношению числа всех проведенных испытаний к числу испытаний, в которых событие А произошло, называется относительной частотой появления события А.
Относительная частота появления события А обозначается: W(А). Таким образом, по определению, 
Замечание. Относительную частоту можно найти, поделив абсолютную частоту на число испытаний. Иногда относительную частоту измеряют в процентах.
Рассмотрим пример: игральный кубик подбросили 50 раз, и исходы испытаний занесли в таблицу, в первом строке которой перечислены все возможные исходы, во второй и третьей строках фиксировались значения абсолютной и относительных частот соответственно
| Исходы | ||||||
| абсолютная частота | ||||||
| относительная частота | 0,18 | 0,12 | 0,16 | 0,22 | 0,18 | 0,14 |
Полученная таблица обладает некоторыми замечательными свойствами, которые характерны для любой таблицы абсолютных и относительных частот:
1) сумма абсолютных частот по всем исходам испытания равна числу проведенных испытаний, для данной таблицы – 50;
2) сумма относительных частот по всем исходам испытания равна 1.
Замечание. Проверка этих свойств поможет в дальнейшем избегать ошибок при заполнении таких таблиц.
Наглядной иллюстрацией распределения абсолютных и относительных частот служат гистограммы, на которых каждая из частот изображается в виде столбика соответствующей высоты. Гистограмма относительных частот для рассмотренного примера изображена на следующем рисунке
По таблице и гистограмме легко оценивать, какой исход в данной серии испытаний появляется чаще остальных. В данном примере видно, что четверка выпадала в этой серии испытаний чаще остальных, а двойка реже. Но можно ли на этом основании сказать, что исход «4» более вероятен, чем исход «2»?
Пусть проводится серия испытаний, и фиксируются абсолютные и относительные частоты исходов испытаний. Выясним, как ведут себя частоты при увеличении числа испытаний в серии. Это удобно наблюдать на конкретном примере.
Пример. Игральный кубик подбрасывали 1000 раз, и после каждой серии из 100 подбрасываний фиксировали относительную частоту появления каждого исхода. В результате была получена следующая таблица.
| Количество испытаний | Частота исходов | ||||
| 0,16 | 0,16 | 0,2 | 0,15 | 0,19 | 0,14 |
| 0,16 | 0,135 | 0,185 | 0,16 | 0,18 | 0,18 |
| 0,167 | 0,16 | 0,163 | 0,153 | 0,183 | 0,173 |
| 0,168 | 0,153 | 0,175 | 0,163 | 0,185 | 0,158 |
| 0,164 | 0,146 | 0,182 | 0,16 | 0,186 | 0,162 |
| 0,152 | 0,157 | 0,183 | 0,153 | 0,188 | 0,167 |
| 0,153 | 0,164 | 0,180 | 0,151 | 0,186 | 0,166 |
| 0,159 | 0,164 | 0,181 | 0,155 | 0,180 | 0,161 |
| 0,156 | 0,164 | 0,183 | 0,166 | 0,171 | 0,160 |
| 0,158 | 0,170 | 0,182 | 0,165 | 0,168 | 0,157 |
Построим график зависимости, например частоты выпадения тройки, от числа экспериментов.
По графику видно, что относительная частота появления тройки вначале проведения серии испытаний испытывает значительные колебания, но с ростом числа испытаний она стабилизируется около значения 0,18. Построив графики зависимостей относительных частот появления других исходов, от числа проведенных испытаний можно убедиться в аналогичном результате. Поэтому, можно сделать вывод, что относительная частота появления той или другой цифры, в данном случае, стабилизируется с ростом числа испытаний.
Оказывается, что такое свойство относительных частот имеет место и в общем случае. Говорят, что с ростом числа однородных испытаний относительная частота появления события приобретает свойство устойчивости, мало отличается от некоторого фиксированного числа. На этом факте основывается одно из определений вероятности.
Определение. Статистической вероятностью события А называется число вокруг которого колеблется относительная частота появления события А в длинной серии испытаний.
Замечание. Следует заметить, что данное определение не является математически строгим, оно скорее, экспериментальное.
Абсолютная частота: формула, расчет, распределение, пример
Содержание:
В Абсолютная частота Он определяется как количество раз, когда одни и те же данные повторяются в наборе наблюдений числовой переменной. Сумма всех абсолютных частот эквивалентна суммированию данных.
Когда у вас есть много значений статистической переменной, их удобно организовать соответствующим образом, чтобы извлечь информацию о ее поведении. Такую информацию дают меры центральной тенденции и меры рассеивания.
В расчетах этих показателей данные представлены через частоту, с которой они появляются во всех наблюдениях.
В следующем примере показано, насколько раскрывается абсолютная частота каждой части данных. В первой половине мая это были самые продаваемые размеры коктейльных платьев из известного магазина женской одежды:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Сколько платьев продается определенного размера, например размера 10? Владельцам интересно знать его на заказ.
Сортировка данных упрощает подсчет, всего имеется ровно 30 наблюдений, которые отсортированы от наименьшего размера к наибольшему следующим образом:
4;4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12;14; 14; 14;16;16; 18; 18
И теперь видно, что размер 10 повторяется 6 раз, поэтому его абсолютная частота равна 6. Такая же процедура проводится для определения абсолютной частоты остальных размеров.
Формулы
Абсолютная частота, обозначаемая как fя, равно тому, сколько раз определенное значение Xя находится в группе наблюдений.
Предполагая, что общее количество наблюдений равно N значениям, сумма всех абсолютных частот должна быть равна этому числу:
Другие частоты
Если каждое значение fя деленное на общее количество данных N, мы имеем относительная частота Fр значения Xя:
Умножение каждого значения f на 100р у тебя есть относительная частота в процентах, сумма которых составляет 100%:
Относительная частота в процентах = (fя / N) x 100%
Также важно накопленная частота Fя с точностью до определенного наблюдения, это сумма всех абсолютных частот до этого наблюдения включительно:
Если накопленную частоту разделить на общее количество данных N, мы получим совокупная относительная частота, который умножается на 100 дает кумулятивная относительная частота в процентах.
Как получить абсолютную частоту?
Чтобы найти абсолютную частоту определенного значения, которое принадлежит набору данных, все они упорядочены от наименьшего к наибольшему, и подсчитывается, сколько раз появляется это значение.
В примере с размерами платьев абсолютная частота размера 4 составляет 3 платья, то есть f.1 = 3. Для размера 6 было продано 4 платья: f2 = 4. В размере 8 также было продано 4 платья, f3 = 4 и так далее.
Табулирование
Общие результаты могут быть представлены в таблице, в которой указаны абсолютные частоты каждого из них:
Очевидно, что лучше упорядочить информацию и иметь возможность получить к ней быстрый доступ, вместо того, чтобы работать с отдельными данными.
Важный: обратите внимание, что при сложении всех значений столбца fявы всегда получаете общее количество данных. Если нет, вам необходимо проверить бухгалтерию, так как есть ошибка.
Расширенная частотная таблица
Приведенную выше таблицу можно расширить, добавив другие типы частот в последовательные столбцы справа:
Распределение частоты
Частотное распределение является результатом организации данных с точки зрения их частот. При работе с большим количеством данных их удобно сгруппировать по категориям, интервалам или классам, каждая со своей соответствующей частотой: абсолютная, относительная, накопленная и процентная.
В примере с размерами данные не сгруппированы, так как это не слишком много размеров, и ими можно легко управлять и учитывать. Таким же образом можно обрабатывать и качественные переменные, но когда данных очень много, лучше всего сгруппировать их по классам.
Распределение частот для сгруппированных данных
Чтобы сгруппировать данные в классы равного размера, примите во внимание следующее:
-Размер, ширина или широта класса: разница между самым высоким значением в классе и самым низким.
Размер класса = Ранг / Количество классов.
-Предел класса: диапазон от нижней границы до верхней границы класса.
-Классовый знак: это середина интервала, который считается представителем класса. Он рассчитывается на основе полусуммы верхнего и нижнего пределов класса.
–Кол-во классов: Формула Стерджеса может быть использована:
Количество классов = 1 + 3,322 log N
пример
Машина на большом заводе вышла из строя из-за повторяющихся сбоев. Последовательные периоды простоя в минутах указанной машины записаны ниже, всего 100 данных:
Сначала определяется количество классов:
Количество классов = 1 + 3,322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Размер класса = Диапазон / Количество классов = (88-21) / 8 = 8,375
Это также десятичное число, поэтому за размер класса принимается 9.
Оценка класса = (29 + 20) / 2 = 24,5
Таким же образом мы ищем метки классов оставшихся интервалов.
Упражнение решено
40 молодых людей указали, что время в минутах, которое они провели в Интернете в прошлое воскресенье, было следующим, в порядке возрастания:
0; 12; 20; 35; 35; 38; 40; 45; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Предлагается построить частотное распределение этих данных.
Решение
Диапазон R набора N = 40 данных:
Применение формулы Стерджеса для определения количества классов дает следующий результат:
Количество классов = 1 + 3 322 журнала N = 1 + 3,32 журнала 40 = 6,3
Поскольку это десятичное число, непосредственное целое число равно 7, поэтому данные сгруппированы в 7 классов. Каждый класс имеет ширину:
Размер класса = Ранг / Количество классов = 220/7 = 31,4
Оценки за класс рассчитываются путем усреднения верхнего и нижнего пределов каждого интервала, например, для интервала [0,35):
Оценка класса = (0 + 35) / 2 = 17,5
Таким же образом поступаем и с другими классами.
Наконец, частоты вычисляются в соответствии с процедурой, описанной выше, в результате получается следующее распределение:
Ссылки
Омепразол: что это такое, показания и побочные эффекты
Курс алгебры в 7-м классе «Относительная частота случайного события»
Разделы: Математика
Оборудование: компьютер, проектор, экран.
I. Самоопределение к учебной деятельности
— На прошлом уроке вы получили задание подготовить сообщение по теме «Что такое теория вероятностей». Давайте заслушаем сообщение.
«Что такое теория вероятностей»
В повседневной жизни в разговоре часто используется слово «вероятность», например: «это невероятный случай», «вероятнее всего он опоздает» и т.д. Здесь интуитивно оценивается возможность того или иного события, исходя из здравого смысла, интуиции. Например, мы заранее знаем, что на детский сеанс пойдет больше школьников, чем взрослых, или, что при выполнении многих видов работ вредна торопливость, т.к. в спешке можно сделать брак.
В задачах, которые мы решаем на уроках математики у всех получается один и тот же ответ. И этот ответ не зависит от способа решения задачи, а зависит только от правильности выполнения вычислений. В реальной же жизни не все так просто. Многие события нельзя предсказать заранее. Мы не можем знать, какая погода будет в первый день весны, когда будет первая гроза. Нельзя наверняка сказать, сколько человек решат позвонить по телефону в ближайший час. Кто может гарантировать, что если я сейчас пойду в магазин, то обязательно встречу там свою одноклассницу. Все эти события могут произойти, а могут не и не произойти. Поэтому эти события называются случайными.
Оказывается, что случайные события тоже имеют свои закономерности, которые изучает раздел математики – Теория вероятностей.
Теория вероятностей неразрывно связана с нашей повседневной жизнью. Она помогает оценить свои шансы на успех, принимать оптимальные решения.
— Сегодня мы начинаем знакомство с очень интересным разделом математики – теорией вероятностей.
1. Устная работа (задания проецируются на экран)
1. Что называется отношением двух чисел? (Отношением двух чисел называется их частное).
2. Найдите отношение чисел:
а) 4 к 8; б) 2 к 
Ответ: а) 0,5; б) 3; в) 4.
3. Из 25 студентов группы 7 отличников. Какой процент всех студентов группы составляют отличники?
4. Из 2000 зерен гороха 1800 оказались всхожими. Определите процент всхожести зерен.
5. Определите процент содержания соли в растворе, если в 300 г раствора содержится 15 г соли.
2. Индивидуальное задание:
За четверть домашнее задание по алгебре было задано 16 раз.
а) Света два раза не сделала домашнее задание. Какова частота невыполнения домашнего задания у Светы за четверть?
б) Женя не сделал домашнее задание девять раз. Какова частота выполнения домашнего задания у Жени за четверть?
III. Выявление причины затруднения и постановка цели деятельности
— В чем причина затруднения? (Не знаем, как определить частоту события).
— Какова цель урока? (Научиться находить частоту события).
— Запишите тему урока: «Относительная частота случайного события».
IV. Изучение нового материала
1. Теоретический материал.
Частота случайного события
Теория вероятностей имеет дело с экспериментами, исходы которых непредсказуемы: они зависят от случая. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно вычислить, как часто оно происходит. Для этого используют важные величины: абсолютную и относительную частоту.
Абсолютная частота показывает, сколько раз в серии экспериментов наблюдалось данное событие.
Относительная частота показывает, какая доля экспериментов завершилась наступлением данного исхода.
Определение. Относительной частотой события А называют отношение абсолютной частоты 
Поскольку 0 ≤ 
При определении относительной частоты случайного события результаты удобно сводить в таблицу.
2. Практическая часть
1) Проведем лабораторную работу (работа в группах по 2 человека.)
Цель работы: определить абсолютную и относительную частоту каждого исхода; выяснить, чему равна сумма абсолютных частот и сумма относительных частот.
Оборудование: игральные кубики, пластмассовые стаканчики.
1. Провести 50 экспериментов по выбрасыванию игрального кубика из закрытого сосуда – стаканчика.
2. Полученные результаты оформить в виде таблицы.
3. Найдите абсолютную и относительную частоты для каждого исхода.
4. Подсчитайте, чему равна сумма абсолютных частот и чему равна сумма относительных частот.
Протокол экспериментального исследования частоты выпадения различных очков игрального кубика.
Относительная частота события
и статистическое определение вероятности
Сегодня мы завершаем изучение первого раздела теории вероятностей, который посвящён основным подходам к определению вероятности, теоремам сложения и умножения событий, а также их основным следствиям. В учебной литературе статистическое определение вероятности обычно рассматривается в первой же главе, но вот мне показалось удачным отложить этот вопрос на заключительный урок по теме. Давайте вспомним, с чего всё начиналось:
Вероятность наступления события 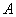
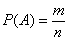
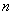
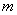
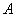
О некоторых недостатках классического определения вероятности заходила речь в статье Геометрическое определение вероятности, но это только верхушка айсберга, и сейчас данный вопрос получит интереснейшее продолжение. Начнём опять же с бесхитростных примеров 1-го урока по теории вероятностей:
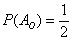
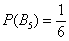
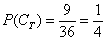
Внимательный читатель заметил, что все комментарии о вероятностях сформулированы в будущем времени. И это не случайность – классическое определение, как правило, оценивает вероятность ДО проведения испытаний и даже без их фактического проведения. То есть, монета ещё не подброшена, а вероятность появления орла мы уже прекрасно знаем. Можно дать зарок никогда не брать в руки кубик либо колоду карт, однако, вероятности событий 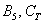
Примечание: однако, в отсутствии информации о результате испытания фразу «Вероятность того, что монета упала орлом» (например) всё же нельзя признать некорректной. То есть классическое определение может оценивать вероятность и после реального опыта.
Почему такое возможно? Такое возможно потому, что все элементарные исходы известны и подсчитаны заранее:
орёл и решка – итого 2 элементарных исхода;
1, 2, 3, 4, 5, 6 – 6 элементарных исходов;
6, 7, 8, 9, 10, В, Д, К, Т каждой масти – всего 36 карт.
Кроме того, для применения классического определения вероятности необходима равновозможность элементарных исходов (см. определение). Равновозможность выпадения граней монеты либо кубика обуславливается симметрией и несмещённым центром тяжести, колода же карт должна быть полной, некраплёной и хорошо перемешанной.
И всё было бы ладно, но в реальной жизни подобные модели встречаются нечасто. В большинстве ситуаций элементарные исходы перечислить затруднительно или невозможно, и ещё труднее обосновать их равновозможность. Простой пример:
Штирлиц пошёл в лес за грибами. Найти вероятность того, что он найдёт подберёзовик.
Кстати, каверзная задачка на счёт равновозможности была в конце урока о теоремах Лапласа. Краткая суть состоит в следующем: если в городе проживает примерно равное количество мужчин и женщин (которых подсчитать значительно проще =)), то это ещё не значит, что вероятность встретить на улице мужчину либо женщину равна 1/2.
Вновь обратим внимание на шаблонные формулировки стандартных задач:
«Стрелок попадает в мишень с вероятностью 0,8»;
«Вероятность изготовления бракованной детали на данном станке составляет 0,05».
Возникает вопрос, откуда взялись эти значения? И ответ здесь один: данные вероятности могли получиться только на основе ранее проведённых опытов.
Относительная частота события и статистическая вероятность
Относительной частотой события 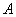
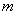
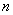
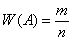
Относительная частота наряду с вероятностью является одним из ключевых понятий тервера, но если классическое либо геометрическое определение вероятности не требуют проведения испытаний, то относительная частота рассчитывается исключительно ПОСЛЕ опытов на основе фактически полученных данных.
В том случае, если серии испытаний проводятся в неизменных условиях, то относительная частота обнаруживает свойство устойчивости, то есть колеблется около определённого значения.
Пусть некий профессиональный стрелок произвёл 100 выстрелов по мишени и попал 83 раза. Тогда относительная частота поражения цели составит: 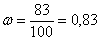
Предположим, что тот же самый стрелок в точно такой же «форме» и в приблизительно таких же условиях снова провёл серию из 100 выстрелов. Вероятно ли, что он снова попадёт 83 раза? Не очень. Но количество попаданий вряд ли будет сильно отличаться от предыдущего результата. Пусть, например, стрелок попал 79 раз. Тогда относительная частота поражения цели составит: 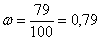
В третьей серии из 100 выстрелов, проведённой при похожих обстоятельствах, данный стрелок попал 81 раз, 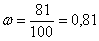
Иногда могут случаться блестящие серии более 90 попаданий, иногда «провалы», но среднее количество попаданий будет варьироваться около 80. И когда количество фактически проведённых испытаний станет достаточно большим, то речь зайдёт о статистической вероятности. Если в одинаковых (примерно одинаковых) условиях проведено достаточно много испытаний, то за статистическую вероятность события принимают относительную частоту данного события либо близкое число.
Предположим, что на протяжении нескольких лет наш спортсмен, сохраняя стабильный уровень подготовки, совершил 10000 выстрелов и попал 8037 раз. Относительная частота поражения цели составит: 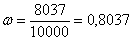
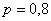
Представьте, что во время лекции этот профессионал зашёл с винтовкой в аудиторию и прицелился. Теперь вам должен стать окончательно понятен смысл фразы «Стрелок попадает в мишень с вероятностью 0,8» =) =)
Именно так собирается богатая спортивная статистика в различных видах спорта.
Аналогичная история с утверждением «Вероятность изготовления бракованной детали на данном станке равна 0,05». Эту оценку невозможно получить с помощью классического определения вероятности – она следует только из практики! Если на станке произведены десятки тысяч деталей и на каждую, скажем, тысячу выпущенных деталей, приходится в среднем 50 бракованных, то в качестве статистической вероятности брака принимается значения 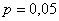
В Задаче 2 урока Локальная и интегральная теоремы Лапласа фигурировала вероятность рождения мальчика 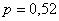
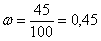
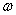
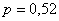
В учебном пособии В.Е. Гмурмана есть весьма удачный пример, в котором продемонстрировано, как при подбрасывании монеты относительная частота появления орла приближается к своей вероятности 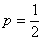
Какой можно сделать вывод? С увеличением количества независимых испытаний случайность превращается в закономерность. Однако следует помнить, что порядок выпадения орлов непредсказуем, о чём я подробно рассказывал на уроке Независимые испытания и формула Бернулли.
Вернёмся к европейской рулетке с 18 красными, 18 чёрными секторами и 1 зеро. В самом примитивном варианте игры: ставим на «красное» или «чёрное», и если шарик остановился на секторе другого цвета (вероятность 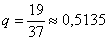
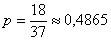
В отдельно взятом сеансе игры отдельно взятый человек может выиграть, причём выиграть по-крупному. Это случайность. Но, совершая миллионы оборотов, рулетка на протяжении веков приносит неизменную прибыль владельцам казино. И это – закономерность. Существует байка о том, что крупный выигрыш не отдадут, а если и отдадут, то «вы с ним не дойдёте до дома». Чистая «киношная» фантазия. Да, кому-то повезло, но сколько проиграется?! К тому же человек, посещающий подобные заведения, с большой вероятностью придёт снова и «сольёт» ещё больше. А чтобы он вернулся, казино, скорее наоборот – создаст максимальный комфорт и безопасность для «счастливчика».
Другой, во многом условный, пример: пусть в некой лотерее приняло участие 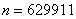
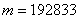
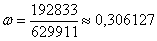
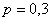
Организатор лотереи знает, что из миллиона проданных билетов выиграют около 300 тысяч с небольшим отклонением. И это закономерность. Но всем участникам лотереи достаётся…. – правильно, случайность! То есть, если вы купите 10 билетов, то это ещё не значит, что выиграют 3 билета. Так, например, выигрыш только по одному билету – есть событие очень даже вероятное, по формуле Бернулли:
А если учесть тот факт, что львиная доля выигрышей – сущая мелочь, то картина вырисовывается совсем унылая, ибо маловозможные события не происходят. Ситуацию спасают красочные телевизионные розыгрыши и различные психологические трюки.
Желающие могут самостоятельно исследовать вероятность выигрыша в различные лотереи – вся статистика есть в свободном доступе. Особо рекомендую подсчитать вероятность крупного выигрыша.
Практическая часть урока будет тесно связана с только что изложенным материалом:
Вероятность отклонения относительной частоты от вероятности
Вероятность того, что в 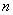
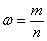
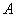
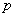
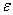
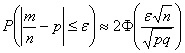
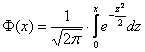
Собственно, эта формула и выведена из интегральной теоремы Лапласа.
Итак, расклад следующий: в распоряжении имеется вероятность 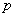
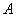
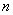
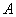
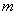
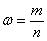
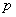
Требуется найти вероятность того, что в серии из 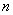
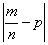
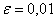
Начнём с самых маленьких :=)
В некотором регионе в результате многолетнего статистического исследования установлена вероятность рождения мальчика 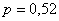
Решение: используем формулу
По условию:
Таким образом:
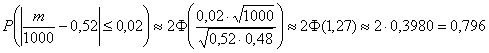
Напоминаю, что значения функции Лапласа можно найти по соответствующей таблице или с помощью расчётного макета (пункт 5).
Ответ:
Каков смысл полученного результата? Если рассмотреть достаточно много групп по 1000 новорожденных в каждой, то примерно в 79,6% этих групп доля мальчиков будет находиться в пределах:
Или, умножая все три части на тысячу: от 500 до 540 мальчиков.
На самом деле рассмотренная задача эквивалентна следующей: «Найти вероятность того, что среди 1000 новорожденных будет от 500 до 540 мальчиков, если вероятность рождения мальчика равна 0,52». А эта задача как раз и решается через известную вам интегральную теорему Лапласа.
Посмотрим на правую часть формулы 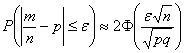
При росте «эн», дробь 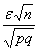
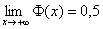
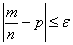
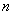
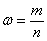
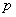
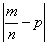
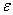
Наоборот – при уменьшении «эн» дробь 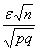
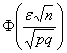
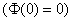
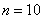
Пара задач для самостоятельного решения:
Производится некоторый опыт, в котором случайное событие 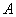
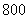
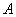
Условие сформулировано в общем виде, как оно чаще всего и бывает. Ещё раз повторим суть задания: проводится 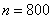
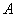
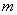
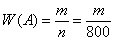
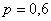
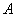
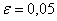
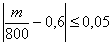
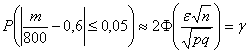
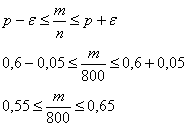
Или в абсолютном количестве появлений события 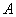
Надо сказать, что границы достаточно вольные и вероятность 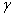
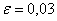
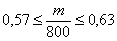
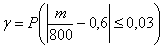
Следующий пример для самых мудрых участников лотереи 🙂
Вероятность выигрыша в лотерею равна 0,3. Продано 600000 билетов. Найти вероятность того, что относительная частота выигрыша отклонится от вероятности выигрыша не более чем на 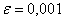
Иными словами, требуется найти вероятность того, что относительная частота выигрыша будет находиться в пределах: 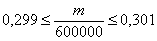
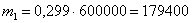
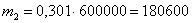
Эта информация очень важнА для корректного распределения призового фонда. Но, повторюсь, пример достаточно условный, т.к. не учитывает правила и ограничения той или иной лотереи.
Краткое решение и ответы в конце урока.
На практике не менее популярна и обратная задача:
Как определить, сколько нужно провести испытаний 
чтобы с заранее заданной вероятностью  обеспечить желаемую точность
обеспечить желаемую точность  ?
?
В предыдущем примере получена довольно высокая вероятность 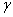
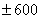
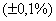
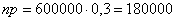
Но, конечно же, хочется, чтобы вероятность 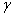
Вероятность выигрыша в лотерею равна 0,3. Сколько билетов должно участвовать в розыгрыше, чтобы с вероятностью не меньшей чем 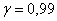
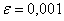
Решение: используем ту же формулу 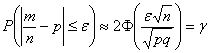
В нашем распоряжении находятся следующие величины:
По условию, требуется найти такое количество билетов 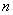
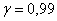
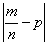
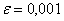
Подставляем известные значения:
Делим обе части на два:
По таблице значений функции 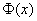
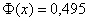
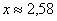
Возведём обе части в квадрат: 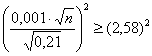
И финальный штрих:
Ответ: для того, чтобы с вероятностью не меньшей чем 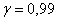
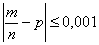
Но это ещё нужно столько продать =) Или же аппетит 
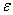
Представим ответ в абсолютных значениях:
То есть, в 99% аналогичных розыгрышей количество выигравших билетов будет заключено в пределах от 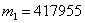
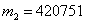
Кстати, выполним проверку, решив прямую задачу: 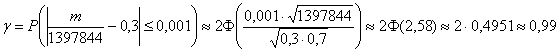
Заключительная миниатюра для самостоятельного решения:
Проводится некоторый опыт, в котором случайное событие 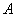
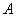
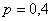
Не ленимся 😉 Ответ в таких задачах следует округлять до бОльшего натурального значения! Краткое решение и ответ внизу страницы.
Первый цикл уроков по теории вероятностей подошёл к концу и даже начал плавно переходить в математическую статистику, так, если в рассмотренной задаче значение 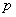
И я уже хотел поставить традиционное пожелание «Везения в главном», но вдруг задумался…. Имеет ли в нашей жизни значение случайность? Безусловно! Нет, я не преуменьшаю значение системной и упорной работы, после которой следуют закономерные результаты. Однако и везение играет немаловажную роль: встретить хороших друзей, встретить «своего» человека, найти деятельность по душе и т.д. – всё это нередко происходит благодаря случаю….
Жду вас снова и до скорых встреч!
Задача 2: Решение: используем формулу 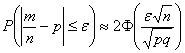
В данной задаче:
а) Если 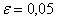
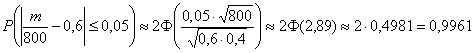
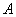
Это событие является практически достоверным.
б) Если 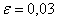
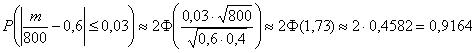
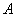
Ответ:
Задача 3: Решение: используем формулу 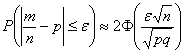
В данной задаче: 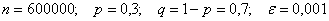
Таким образом:
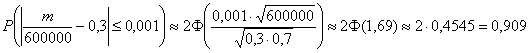
Ответ:
Задача 5: Решение: используем формулу 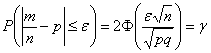
В данном случае: 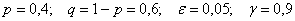
Таким образом: 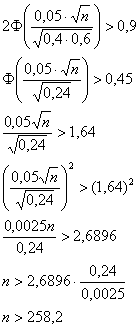
Ответ: необходимо произвести не менее 259 опытов.
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5





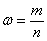
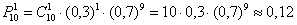
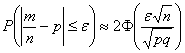
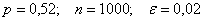
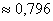
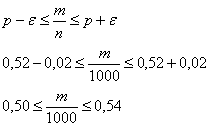
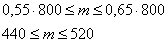
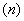
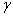 обеспечить желаемую точность
обеспечить желаемую точность 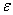 ?
?