Что такое 2пр в математике

Площадь круга

Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..

Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.

Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:

Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.

Источник

Площадь круга: как найти, формулы

площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ

Определение основных понятий

Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.

Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.

Формула вычисления площади круга

Давайте разберем несколько формул расчета площади круга. Поехали!

Площадь круга через радиус

Площадь круга через диаметр

S = d 2 : 4 × π, где d — это диаметр.

Площадь круга через длину окружности

S = L 2 ​ : (4 × π), где L — это длина окружности.

Популярные единицы измерения площади:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Задачи. Определить площадь круга

Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!

Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.

Диаметр окружности равен двум радиусам.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 12 2 : 4.

Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.

Используем формулу: S = π × d 2 : 4.

Подставим известные значения: S = 3,14 × 90 2 : 4.

Задание 3. Найти длину окружности при радиусе 3 см.

Отношение длины окружности к диаметру является постоянным числом.

Получается: L = d × π.

Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.

Подставим значение радиуса: L = 2 × 3,14 × 3.

Источник

2 Пи р квадрат это формула

Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:

S=πr 2 – это произведение числа пи на квадрат радиуса.

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .

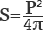
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.

Перевод радиан в градусы.
A_d = A_r * 180 / пи
Где A_d — угол в градусах, A_r — угол в радианах.

Перевод градусов в радианы.
A_r = A_d * пи / 180
Где A_d — угол в градусах, A_r — угол в радианах.

Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.

Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.

Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.

Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.

Площадь сектора.
S = L_d * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, L_d — длина дуги.

Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.

Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.

Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.

Содержание

История [ править | править код ]

Использование многоугольников [ править | править код ]

Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]

Доказательство Архимеда [ править | править код ]

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше [ править | править код ]

Предположим, что площадь круга C больше площади треугольника T = 1 ⁄₂cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈. Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T E&<>=C-T\&<>>G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>> G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>»/>

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄₂nhs. Но h 1 ⁄₂cr, получили противоречие.

Не меньше [ править | править код ]

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника P_n должна быть меньше T.

G_ \P_ &<>=C+G_ \&<> D = T − C > G n P n = C + G n C + D P n T =T-C\&<>>G_ \P_ &<>=C+G_ \&<> G_ \P_ &<>=C+G_ \&<>

Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.

Таким образом, площадь круга в точности равна площади треугольника.

Доказательство перегруппировкой [ править | править код ]

многоугольник			параллелограмм
n	сторона	основание	высота	площадь
4	1,4142136	2,8284271	0,7071068	2,0000000
6	1,0000000	3,0000000	0,8660254	2,5980762
8	0,7653669	3,0614675	0,9238795	2,8284271
10	0,6180340	3,0901699	0,9510565	2,9389263
12	0,5176381	3,1058285	0,9659258	3,0000000
14	0,4450419	3,1152931	0,9749279	3,0371862
16	0,3901806	3,1214452	0,9807853	3,0614675
96	0,0654382	3,1410320	0,9994646	3,1393502
∞	1/∞	π	1	π

Интегрирование [ править | править код ]

Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.

Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:

Быстрая аппроксимация [ править | править код ]

Метод удвоения Архимеда [ править | править код ]

Если задан круг, пусть u_n будет периметром вписанного правильного n-угольника, а U_n — периметром описанного правильного n-угольника. Тогда u_n и U_n являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (u_n + U_n)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить u_n и U_n для больших n, Архимед вывел следующие формулы:

u 2 n = U 2 n u n = u_ >>> (среднее геометрическое) U 2 n = 2 U n u n U n + u n = u_ > +u_ >>> (среднее гармоническое).

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.

В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u₆ = 6, а описанный шестиугольник имеет периметр U₆ = 4√3. Удваиваем семь раз, получаем

knu_nU_n(u_n + U_n)/466,00000006,92820323,23205081126,21165716,43078063,16060942246,26525726,31931993,14614433486,27870046,29217243,14271824966,28206396,28542923,141873351926,28290496,28374613,141662863846,28311526,28332553,141610277686,28316786,28322043,1415970

Улучшение Снелла-Гюйгенса [ править | править код ]

Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:

Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.

Развитие формулы удваивания Архимеда [ править | править код ]

В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+ 1 ⁄₂c_n, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена

Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону S_n, тогда отношение превращается в S_n : s_n = 1 : 1 ⁄₂c_n. (Мы снова используем факт, что OP равен половине A′B.) Получаем

Обозначим периметр вписанного многоугольника через u_n = ns_n, а описанного через U_n = nS_n. Комбинируя равенства, получим

Можно также вывести

Аппроксимация случайными бросаниями [ править | править код ]

Конечная перегруппировка [ править | править код ]

Обобщения [ править | править код ]

Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.

Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π /4, и отношение площади эллипса к площади прямоугольника будет тоже π /4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — π ab/4.

Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.

Источник

Число Пи — это математическая постоянная

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы подробно расскажем, что такое число «пи», которое частенько используется в математике.

На самом деле, это постоянная величина, которая помогала еще древним Египтянам проводить расчеты при проектировании. Она, например, позволяла, зная диаметр окружности, легко рассчитать ее длину (периметр).

Но вот только значение этой постоянной в те времена точно рассчитать не получалось. Сегодня же мы можем узнать чему равно число ПИ вплоть до триллионного знака после запятой.

Что такое число Пи

Впервые школьники сталкиваются с этим понятием еще в 3-м классе, когда начинают изучать окружность (что это?).

Им просто говорят, что какую бы окружность они не нарисовали, если поделить ее длину на диаметр, то получится одно и то же число. И называется это число «пи», обозначается латинской буквой «π» и равно 3,14.

Кстати, именно так и звучит официальное определение числа «пи»:

Пи – это математическая константа (постоянная), которая равна отношению длины окружности к ее диаметру.

А вот в 6-м классе школьников ближе знакомят с этим числом. Именно тогда начинают изучать формулы длины и площади окружности. А в них без «пи» не обойтись:

История возникновения числа «пи»

Ученые считают, что еще в Древнем Египте знали о существовании некой математической постоянной. Этот вывод сделали на основании папирусов, на которых расписаны вычисления площади круга. И в ней фигурировало некое число, которое равнялось 3,160.

Но число, напоминающее «пи» встречается и в других странах:

Эта греческая буква взята неслучайно, она первая в словах «περιφέρεια» (окружность) и «περίμετρος» (периметр).

И наконец, общепринятым понятие «математической постоянной» стало в 1737 году после публикации научных работ Леонардо Эйлера.

Чему равно число Пи

Количество знаков после запятой у числа «пи» бесконечно.

Во всяком случае, ни один компьютер (это что?) до сих пор так и не смог вычислить их до конца. Самая современная вычислительная машина смогла показать лишь 10 триллионов цифр.

И что наиболее любопытно, в этом огромном количестве цифр нет никакой зависимости или тенденции. Математики очень любят разбивать знаки после запятой на группы по 10 цифр. И вот среди этих групп у числа «пи» невозможно найти две одинаковые.

На рисунке ниже приведено значение числа Пи с точностью до 1000 знаков после запятой:

Число «пи» в фольклоре

Чтобы запомнить побольше знаков числа «пи» люди пользуются разными приемами мнемотехники.

Например, есть такие стихотворения:

Чтобы нам не ошибиться,
Надо правильно прочесть.
Три, четырнадцать, пятнадцать.
Девяносто два и шесть.

А есть специальные стихи, в которых числа определяются по количеству букв в словах:

Это(3) я(1) знаю(4) и(1) помню(5) прекрасно(9).
Пи(2) многие(6) знаки(5) мне(3) лишни(5), напрасны(8).
Доверимся(9) знаньям(7) громадным(9)
Тех(3), пи(2) кто(3) сосчитал(8), цифр(4) армаду(6).

Называние «пи» присутствует и в нескольких фильмах. Например, в 1998 году режиссер Даррен Аронофски снял картину «Пи». Это психологический триллер, в котором главный герой считает, что все в жизни можно описать с помощью чисел. Но в результате он чуть не сошел с ума.

А в 2012 году на экраны вышел фильм «Жизнь Пи». Он, правда, не имеет ничего общего с математикой. Это приключенческая лента о путешествиях индийского юноши по имени Пи.

С 1987 году математики даже отмечают День числа «пи». Происходит это 14 марта, так энтузиасты обыграли первые цифры (3,14). А начало торжеств приходится на определенное время – 01:59. Это также дань цифрам, которые идут после запятой.

Празднования проходят, как правило, скромно. Люди просто готовят круглый торт, садятся за круглый стол и делятся забавными историями, связанными с числом «пи» и математическими задачками в целом.

И наконец, есть даже анекдоты на тему числа «пи». Один из таких звучит так:

Один ученый спрашивает другого:
— Скажи, а почему рельсы прямые, колеса круглые, а когда поезд едет, то они стучат?
— Ну, это просто. Колеса же круглые. А значит, их площадь равна «пи эр квадрат». Вот тот самый квадрат и стучит.

Вот и все, что мы хотели рассказать о числе «пи». До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (3)

Приведенное выше число пи не точное (приближенное)

ТОчное значение этого числа 3,14269680. Это доказано в статье «Через центр масс квадранта к числу пи» см. в Инете

Самое забавное, что мы не можем вычислить точную площадь круга, именно потому что число Пи бесконечно.

Вроде бы Архимед нашел свое число Пи следующим образом, он брал два многоугольника, один был вписан в окружность, а сама окружность была вписана во второй многоугольник, затем он находил периметры этих двух многоугольников и брал их отношение, потом он увеличивал количество сторон этих многоугольников и они все больше становились похожи на окружность, так он и получил наиболее точное значение своего числа.

Да зачем нужны эти триллионы после запятой? Вот учёным делать нечего, всё равно погрешность изготовления окружности будет выше этой точности.

Источник