Что такое 2пн в тригонометрии
Решение тригонометрических уравнений — 39 примеров!
Привет, самый лучший ученик во Вселенной!
Сегодня мы с тобой изучим, как решать одну из разновидностей уравнений – тригонометрические. Мы решим 39(!) примеров, от самых простых, до самых сложных.
И станем на шаг ближе к заветной цели – сдать ЕГЭ по математике так, чтобы поступить в ВУЗ мечты!
Тригонометрические уравнения — коротко о главном
Тригонометрическое уравнение – это уравнение, в котором неизвестная находится строго под знаком тригонометрической функции.
Существует два способа решения тригонометрических уравнений:
Первый способ – с использованием формул.
Второй способ – через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.
Чтобы уметь решать тригонометрические уравнения необходимо знать как минимум следующее:
Если ты что-то не знаешь, повтори следующие разделы:
Этого будет вполне достаточно. Если это по ходу моего повествования окажется не так, то не сердись, придётся вспомнить что-нибудь ещё, не упомянутое здесь.
Простейшие тригонометрические уравнения
Что же это такое, как ты думаешь? Является ли, например, уравнение
Ты и сам прекрасно понимаешь, что нет! Потому что ни одной тригонометрической функции \( \displaystyle \left( sin x,cos x,tg x,ctg x \right)\) в нём и в помине нет!
А что насчёт вот такого уравнения?
И опять ответ отрицательный!
Это так называемое уравнение смешанного типа.
Оно содержит как тригонометрическую составляющую, так и линейную (\( \displaystyle 3x\)).
Некоторые типы подобных уравнений мы будем с тобой решать в следующих раздела этой статьи.
Но вернёмся к вопросу: «Что же такое тригонометрические уравнения?»
Тригонометрические уравнения –это уравнения, в которых неизвестная находится строго под знаком тригонометрической функции!
Однако для начала мы не будем решать сложные и иногда неприступные тригонометрические уравнения, а ограничимся самыми простыми уравнениями вида:
Где \( \displaystyle a\) – некоторое постоянное число.
Например: \( \displaystyle 0,5;
\( \displaystyle f\left( x \right)\) – некоторая функция, зависящая от искомой переменной \( \displaystyle x\), например \( \displaystyle f\left( x \right)=x,
f\left( x \right)=\frac<\pi x><7>\) и т. д.
Такие уравнения называются простейшими!
Основная цель решения ЛЮБОГО тригонометрического уравнения – это свести его к виду простейшего!
Для этого, как правило, используют аппарат, который я описал в разделе «Формулы тригонометрии«
Так что очень важно, я бы даже сказал, жизненно необходимо научиться решать простейшие уравнения, ибо они – фундамент для решения сложных примеров.
Как часто тригонометрические уравнения встречаются на ЕГЭ?
Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:
Так что, как ты понимаешь, при некоторых раскладах, навык решения данного вида уравнений может добавить в твою копилку аж 5 первичных баллов из 32!
Два способа решения тригонометрических уравнений – через формулы и по кругу
В принципе, я не могу сказать, что легче: держать в голове, как строится круг, или помнить 4 формулы.
Тут решать тебе самому, однако я всё же предпочитаю решать данные уравнения через формулы, поэтому здесь я буду описывать именно этот метод.
Вначале мы начнём с «самых простейших» из простейших уравнений вида:
Я хочу сразу оговориться вот о чем, будь внимателен:
То есть, тебе не надо знать вообще никаких формул, чтобы спокойно ответить, что уравнения, например:
\( \displaystyle cos\left( 3
\( \displaystyle sin\left( 2<
Корней не имеют.
Потому что они «не попадают» в промежуток от минус единицы до плюс единицы.
Ещё раз скажу: внимательно обдумай эти слова, они уберегут тебя от многих глупых ошибок.
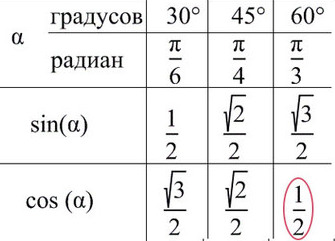
Для остальных же случаев тригонометрические формулы такие как в этой таблице.
На самом деле в этой таблице данных немного больше, чем нужно.
Тебе нужно лишь запомнить первые два её столбца, другие столбцы – частные случаи решения тригонометрических уравнений.
Я, допустим, никогда не утруждаю себя их запоминанием, а вывожу ответ из основных формул.
Глядя на таблицу, не возникло ли у тебя пары вопросов?
У меня бы возникли вот какие:
Что такое \( \displaystyle n\) и что такое, например \( \displaystyle arcsin\alpha
Отвечаю на все по порядку:
В чем уникальная особенность тригонометрических уравнений перед всеми остальными, которые ты изучал?
ОНИ ИМЕЮТ БЕСКОНЕЧНОЕ КОЛИЧЕСТВО КОРНЕЙ.
И число \( \displaystyle n\) и служит для обозначения этой «бесконечности».
Конечно, вместо \( \displaystyle n\) можно писать любую другую букву, только не забывай добавить в ответе: \( \displaystyle n\in Z\) – что означает, что \( \displaystyle n\) – есть любое целое число.
Теперь насчёт арксинуса и других «арок». Вообще, так записываются обратные тригонометрические функции и понимать, скажем, \( \displaystyle arcsin\alpha \) надо как «угол, синус которого равен \( \displaystyle \alpha \)«
Алгоритм вычисления арксинусов и других «арок»
Вот простой пример вычисления аркосинуса:
\( \displaystyle \arccos \left( \frac<\sqrt<3>> <2>\right)\)
\( \displaystyle \frac<\pi ><6>\) и \( \displaystyle \frac<\pi ><3>\).
Если «арка» берется от отрицательного числа?
Всё ли я сказал про «арки»? Почти что да! Остался вот какой момент.
Что делать, если «арка» берётся от отрицательного числа?
Лезть в таблицу – как бы не так! Для арок выполняются следующие формулы:
И внимание.
Чтобы запомнить, ориентируемся на обычные тригонометрические функции: грубо говоря, синус и тангенс мы смотрим на тригонометрической окружности по вертикальной оси, а косинус и котангенс – по горизонтальной.
Соответственно, для арксинуса и арктангенса выбираем две четверти по вертикали: первую и четвёртую (минусик выносится из аргумента и ставится перед функцией), а для арккосинуса и арккотангенса – по горизонтали: первую и вторую.
В первой и второй четвертях аргумент уже не может быть отрицательным, поэтому и получаются формулы не совсем похожими.
Ну всё, теперь мы можем приступать к решению простейших уравнений!
Решение 11-ти простейших тригонометрических уравнений
Уравнение 1. \( \displaystyle sin\left( x \right)=0,5\)
Запишу по определению:
Всё готово, осталось только упростить, посчитав значение арксинуса.
Что такое 2пн в тригонометрии
Методы решения тригонометрических уравнений.
1. Алгебраический метод.
( метод замены переменной и подстановки ).
2. Разложение на множители.
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
3. Приведение к однородному уравнению.
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на
cos ( или sin ) в старшей степени;
1) tan x = –1, 2) tan x = –3,
4. Переход к половинному углу.
5. Введение вспомогательного угла.
6. Преобразование произведения в сумму.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Тригонометрические уравнения

Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
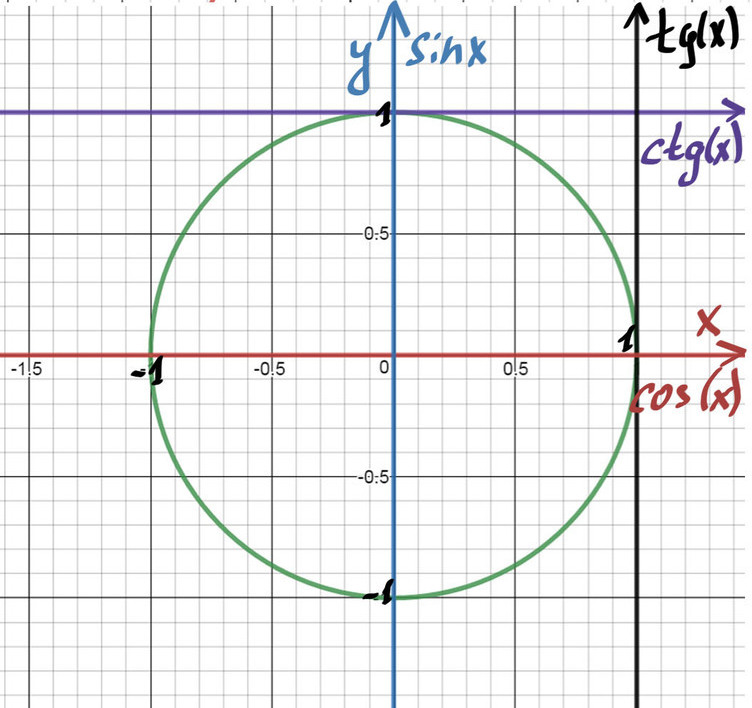
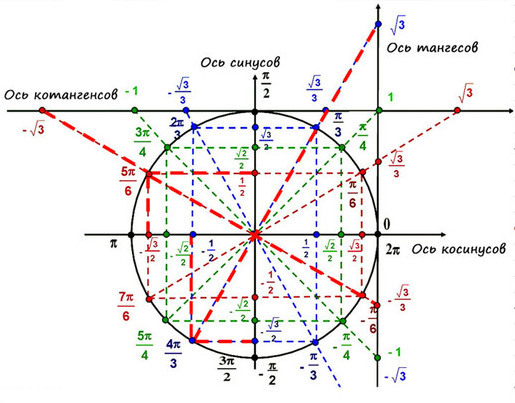
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
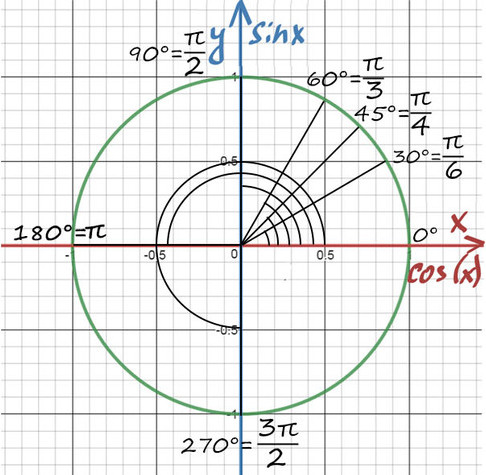
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
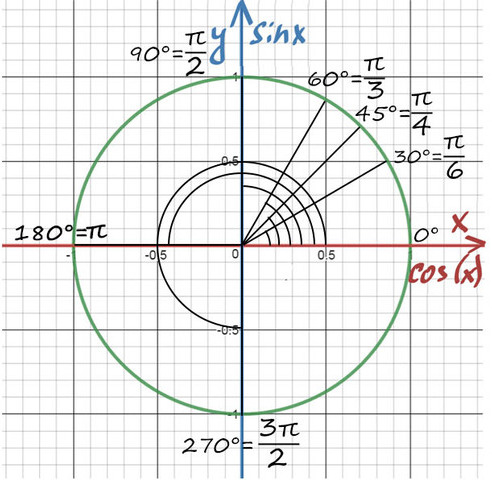
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
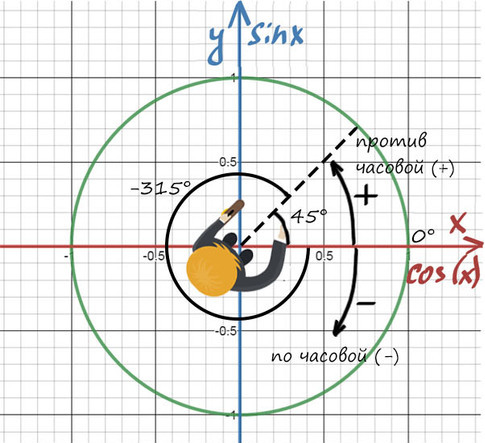
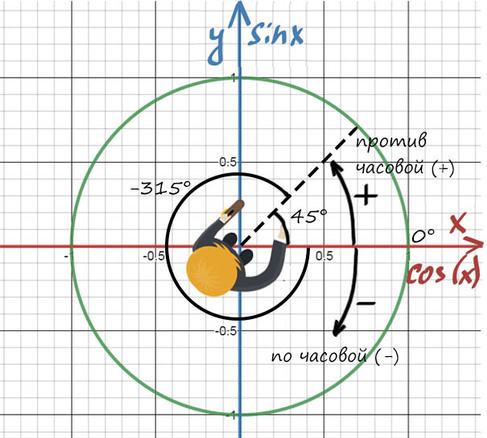
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
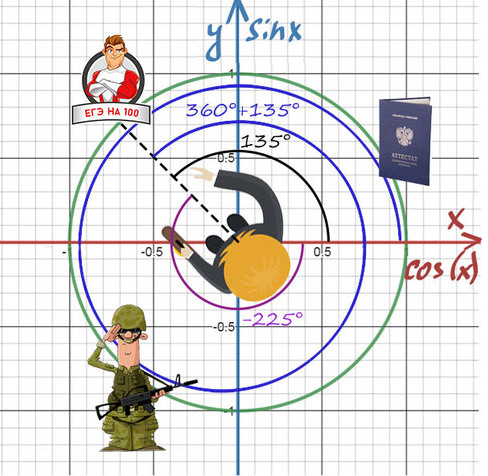
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
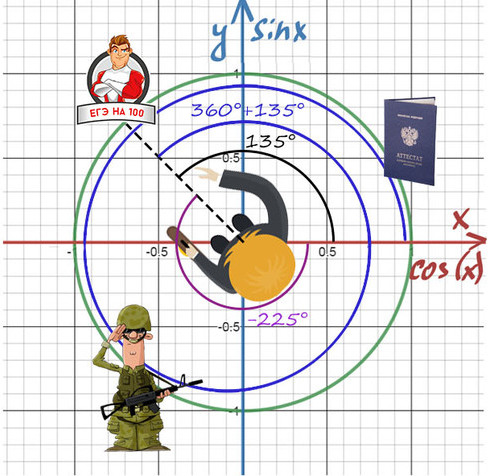
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
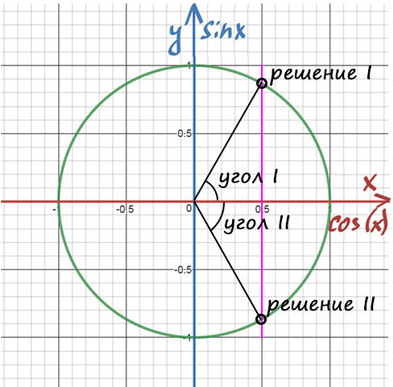
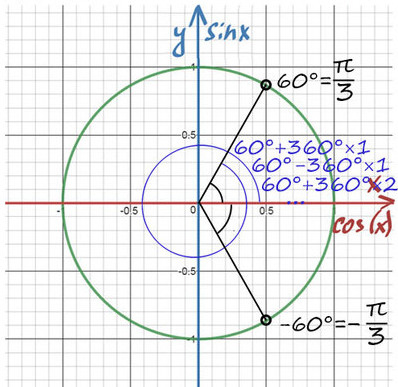
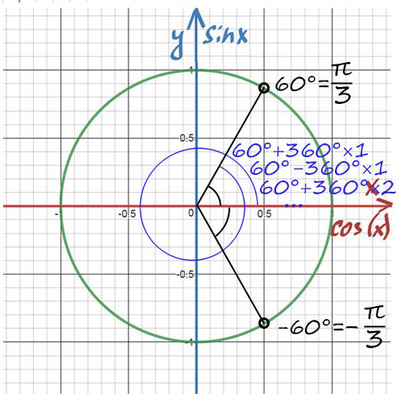
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
Или запомнить такой прием:
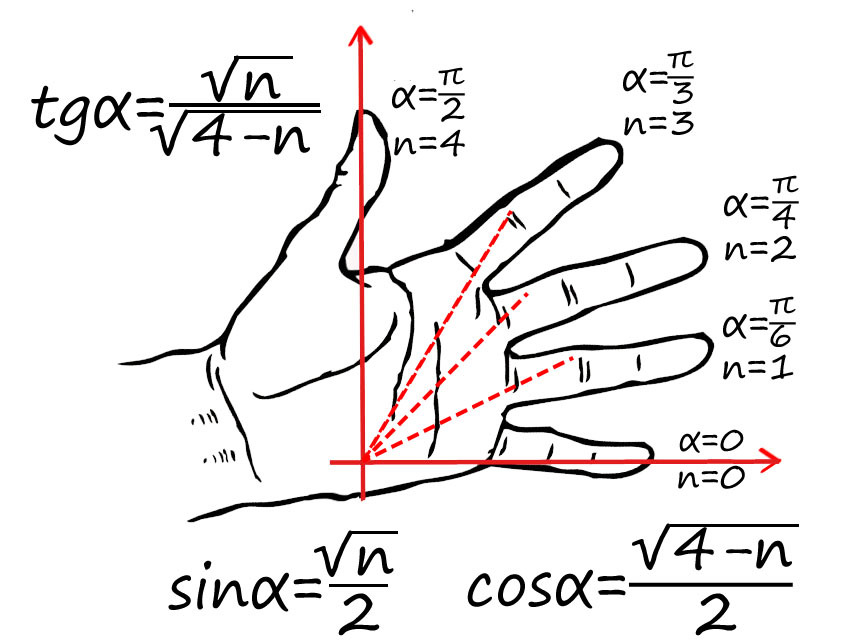
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
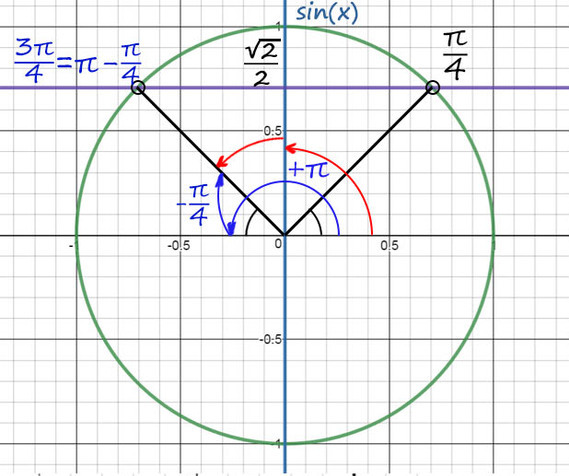
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
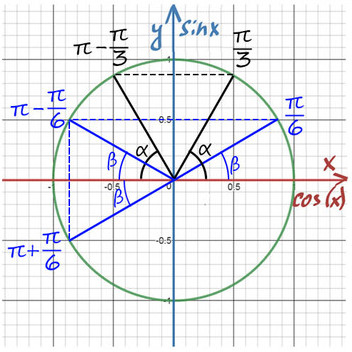
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
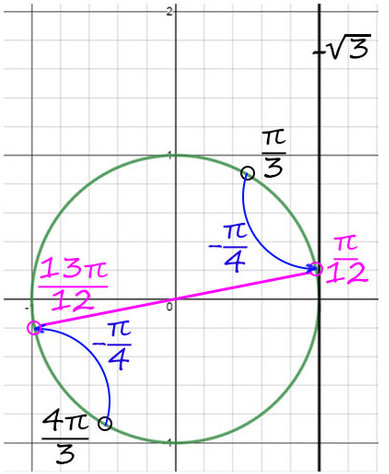
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
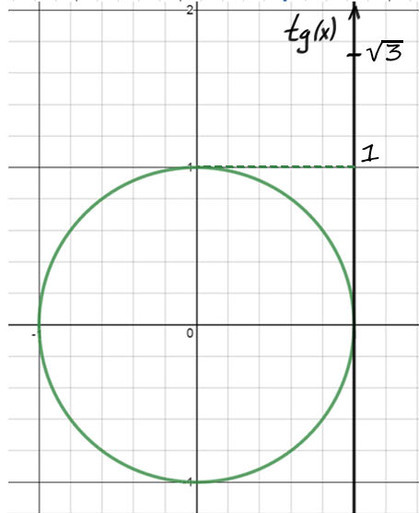
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
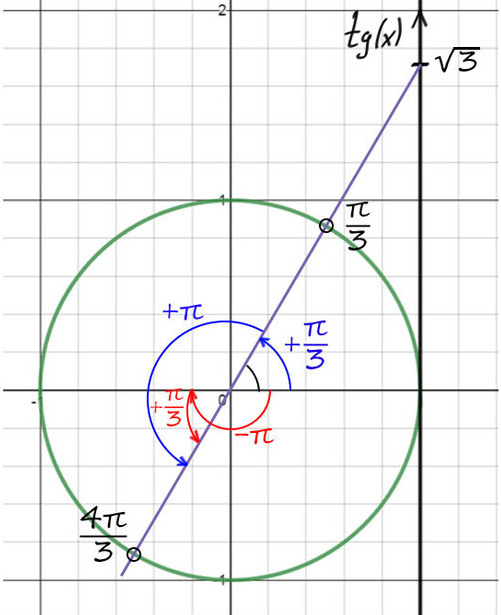
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
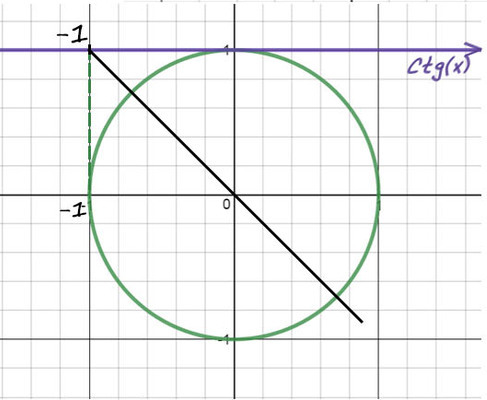
Пример №4: −10ctg(x) = 10
1) Проведем прямую через эту точку и начало координат.
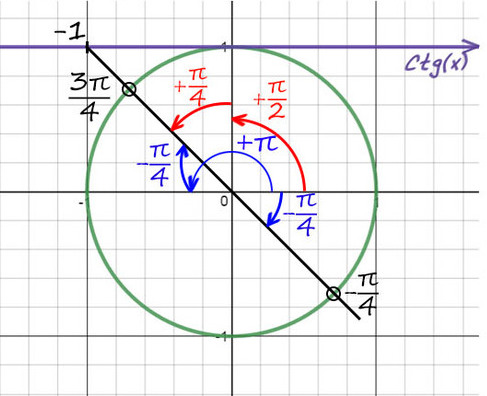
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :