Что такое 180 градусов
Правило 180 градусов в кино: описание, тонкости, соблюдение и нарушение правила
В мире кино, как и при съёмке видео в других сферах, существует масса правил и секретов, которые следует обязательно соблюдать для создания по-настоящему качественного контента. Одной из наиболее распространённых тонкостей съёмки видео является правило 180 градусов (иногда называют правилом красной линии). Что значит данное правило и как его не нарушать? Предлагаем вместе разобраться в нашей статье.
Понятие и описание правила
Правило 180 градусов – один из обязательных моментов в кинематографе, который регламентирует экранные пространственные соотношения между персонажами или между персонажем и объектом. В данном случае визуально проводится ось между персонажами (или объектом), и съёмка камеры должна осуществляться только с одной стороны этой линии. Если видеокамера располагается между персонажами, то на экране первый герой всегда будет слева по отношению ко второму (и наоборот).
Важно! Процесс перемещения камеры через ось называют переходом линии, а постоянные переходы – стрельбой по кругу.
Правило красной линии даёт зрителям возможность визуально ощущать невидимые движения, которые происходят вокруг непосредственного объекта, что крайне важно при съёмке батальных сцен.
Важно! Для качественной съёмки видео нужны профессиональные камеры, которые позволили бы максимально реалистично передавать картинку и происходящие события. На сайте tvtok.ru можно взять в аренду необходимое операторское оборудование по наиболее приятным ценам.
Примеры использования правила
Если видеокамера остаётся с одной стороны воображаемой линии, то пространственное отношение между персонажами будет постоянным во всех кадрах, даже если на экране показывают одного героя. При переходе за эту ось порядок расположения объектов изменится слева направо, что дезориентирует зрителя. Ещё один пример соблюдения правила 180 градусов – съёмка одного героя при его движении. Если персонаж двигается вправо и нужно захватить его другой видеокамерой, то он должен «выйти» из предыдущего кадра справа, а в последующий фрейм «войти» слева.
Переходы линий часто используются, чтобы обозначить время. Если герой покинул кадр с правой стороны, и в новый фрейм «вошёл» также справа, но уже в другом месте, то благодаря этому создаётся иллюзия прохождения некоторого временного отрезка. Ещё один пример – автомобильные погони: если машина покидает левую часть экрана в кадре, то в следующем фрейме она должна заехать с правой стороны экрана. При «выходе» и «входе» слева будет создаваться такая же дезориентация, как во время диалогов.
Переход линии и обратный ракурс
Воображаемая ось даёт возможность зрителю ориентироваться в пространстве касательно положения персонажей и направления действия конкретной сцены. Если на двух соседних кадрах герой или объект находится с противоположной стороны от оси, этот эффект называют «обратным отсечением (ракурсом, разрезом)».
Существуют различные способы избежать путаницы и дезориентации зрителя из-за пересечения линии при особых ситуациях или действиях на экране:
Иногда правило 180 градусов нарушают по техническим причинам (например, если возможно физически поставить камеру в нужном положении) – в таких ситуациях операторы часто пытаются скрывать ошибки. Так, редакторы могут предварительно замыкать слова в диалогах или вырезать переднюю часть фраз, чтобы зрители сконцентрировались на более важных словах, чтобы отвлечь их от нарушенного правила красной линии.
Нарушение описываемого правила могут использоваться для вызова эмоций или создания визуальных ритмов. Так, при перемещении камеры ближе к воображаемой линии при съёмке крупным планом обеспечивается усиление интенсивности сцены за счёт длительного снимка. И наоборот – перемещение камеры дальше от линии при длительном снимке после крупного плана позволяет прервать действие сцены.
Обязательно ли соблюдать правило 180 градусов
Соблюдение правила 180-градусного ограничения в кадре позволяет удерживать героев на «правильной» стороне. При нарушении этого внимание зрителей отвлекается от сцены, нарушая ход событий. А при экстраполировании можно изменять ритм либо эмоцию сцены. Это лишь субъективные утверждения кинематографистов, а не результат эмпирических доказательств.
Но на практике была проведена масса исследований, которые доказывают и визуально подтверждают, почему пересечение воображаемой оси негативно влияет на пространственное представление сцен. Нарушения данного правила искажают пространственные параметры персонажей и объектов (расположение в сцене), но не оказывают влияния на ход повествования и последовательность событий.
Таким образом, эмпирические исследования указывают на то, что практический смысл соблюдения правила красной градусов является необязательным. Точное пространственное представление неважно для сцен, поскольку оно не запоминается зрителями в течение фильма. При этом в ходе недавних исследований было доказано, что даже если зрители замечают нарушения перехода оси, это не ухудшает удовольствие от сцен или фильмов.
В каких фильмах было использовано или нарушено правило
Несмотря на необязательность, в профессиональном кинопроизводстве операторы предпочитают соблюдать правило красной линии. Но иногда режиссёры намеренно прерывают действия, чтобы дезориентировать зрителя. Яркие примеры этого:
Нарушением правила часто «грешат» сёстры Вачовски, Жак Тати, Жак Деми, Ясуджиро Одзу, Тинто Брасс, Вонг Кар-вай и многие другие режиссёры.
Важно! В японском аниме «Паприка» в одной из сцен главные герои обсуждают и демонстрируют эффект дезориентации при пересечении воображаемой оси.
Правило 180 градусов является одним из главных в мире кинематографа. Его желательно всегда соблюдать, а нарушать только для создания определённого эффекта или изменения направления сцены.
Что такое градусы, угловые минуты и угловые секунды?
Как небесные наблюдатели измеряют расстояния в ночном небе? И как это понимать, когда они говорят об объектах, находящихся на расстоянии нескольких градусов (или нескольких угловых минут или угловых секунд) друг от друга.
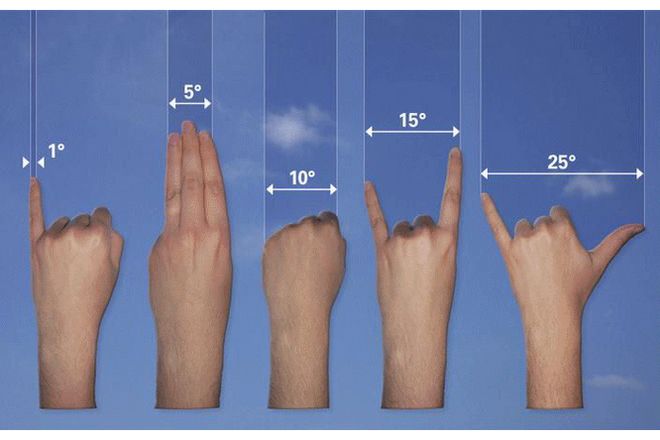
Самый удобный измерительный прибор для измерения небесного свода всегда с вами, на конце вашей руки.
Вы можете использовать ширину вашего мизинца, кулака и расстояние между пальцами руки. Чтобы измерить расстояние между небесными объектами.
Это очень удобно, когда вы наблюдаете за планетами и звездами, или планетами, звездами и Луной. А также другими космическими объектами.
Вы часто обнаружите, что эти объекты описываются как находящиеся на некотором расстоянии друг от друга в градусах, дуговых минутах или дуговых секундах.
Насколько это далеко друг от друга?
Начнем с того, что от одной стороны неба до другой горизонт измеряется 180 градусами, или полукругом. Поэтому от горизонта до зенита, точки прямо над головой, должно быть 90 градусов. Если вы находитесь на ровной местности с ровным горизонтом. А не в холмистом или горном районе.
“подручное”средство для измерения градусов на небосводе. Изображение Астрономического общества Форт-Уэрта
Общее правило астрономов-любителей состоит в том, что ширина вашего кулака, удерживаемого на расстоянии вытянутой руки, равна примерно 10 градусам. Вы можете смотреть на свой кулак и кулак маленького ребенка и удивляться. Как оба могут измерять 10 градусов, но размер кулаков людей обычно пропорционален длине их рук. Таким образом, ребенок с маленьким кулаком и маленькой рукой будет измерять приблизительно 10 градусов с их точки зрения. Так же как взрослый с большим кулаком и более длинной рукой измеряет 10 градусов с их точки зрения.
Если вы хотите сделать грубую проверку, вытяните руку и кулак к горизонту. Затем положите вторую руку и кулак поверх первой и чередуйте, стараясь не раскачиваться, пока не насчитаете девять кулаков. Ваш девятый кулак должен быть направлен прямо вверх.
Для градусов меньше 10 вам будет достаточно только пальцев. На расстоянии вытянутой руки мизинец измеряет от 1 до 1,5 градусов. А три средних пальца около 5 градусов. Для больших углов вам нужно будет раздвинуть пальцы. Чтобы найти 15 градусов, используйте указательный палец и мизинец, разведенные в стороны. А чтобы найти 25 градусов, посмотрите на промежуток между мизинцем и большим пальцем, разведенными в стороны.
Большая Медведица – хороший пример для проверки ваших измерений
Последние две звезды в чаше, те, которые используются для поиска полярной звезды. Они находятся примерно в 5 градусах друг от друга. Две верхние звезды в чаше Большой Медведицы находятся на расстоянии 10 градусов друг от друга. И, наконец, используя ту же самую далекую звезду в чаше Большой Медведицы, которую вы использовали для первых двух тестов плюс конечную звезду в ручке, вы отмерите 25 градусов.
Как вы думаете, насколько широко выглядит полная луна – сколько градусов она занимает? 5 градусов? Большинство людей переоценивают его размеры. Но на самом деле полная луна имеет всего пол-градуса в поперечнике.
А как насчет солнца? Хотя инстинктивно вы можете сказать, что солнце больше. Потому что его фактический размер огромен, если поставить его рядом с Луной. Однако площадь, которую занимают солнце и луна, равно полу-градусу. Вы можете догадаться об этом, даже не проверяя солнце с помощью ваших мизинцевых измерений. Потому что вы наверняка знаете, что во время полных солнечных затмений луна временно скользит прямо перед солнцем. Блокируя весь его свет на несколько коротких минут.
Теперь, когда у вас есть представление о градусах. Если вы хотите оценить меньшие расстояния, вам нужно знать, что градусы далее делятся на минуты. В 1 градусе 60 угловых минут, поэтому и луна и солнце имеют 30 угловых минут в поперечнике. Угловые минуты также можно разделить. 60 угловых секунд составляют 1 угловую минуту.
Возвращаясь к Большой Медведице, звезды в изгибе ручки представляют собой двойную звездную систему под названием Мицар и Алькор. Они разделены всего 12 дуговыми минутами. Люди с хорошим зрением могут видеть две отдельные звезды без помощи оптических приборов. У Мицара есть еще один спутник, который еще ближе, чем Алькор. Двойная звезда Мицара находится всего в 14,4 угловых секундах. Минуты угла записываются символом ( ‘ ), а секунды записываются символом ( ” ).
Вы можете сказать, сколько времени до захода солнца, измерив его расстояние от горизонта. Солнце движется по небу примерно на 15 градусов за час. Движение на 15 градусов в час в течение 24 часов будет равно 360 градусам, или целому дню от заката до заката.
закат над Тадж-Махалом, фото Абхинав Сингхай
Конечно, солнце на самом деле не движется. Это только кажется, что оно движется в небе. Помните, что если вы не находитесь на экваторе, солнце не движется прямо к горизонту. Солнце опускается вниз под углом, который становится круче, чем ближе вы находитесь к полюсам.
Градусы, угловые минуты и угловые секунды, все это полезные единицы измерения в астрономии. Иногда даже ваша собственная рука может вам помочь произвести измерения помочь.
Углы 30, 45, 60, 90 градусов: наглядные, стихотворные, боевые, электрические, драматические, музыкальные
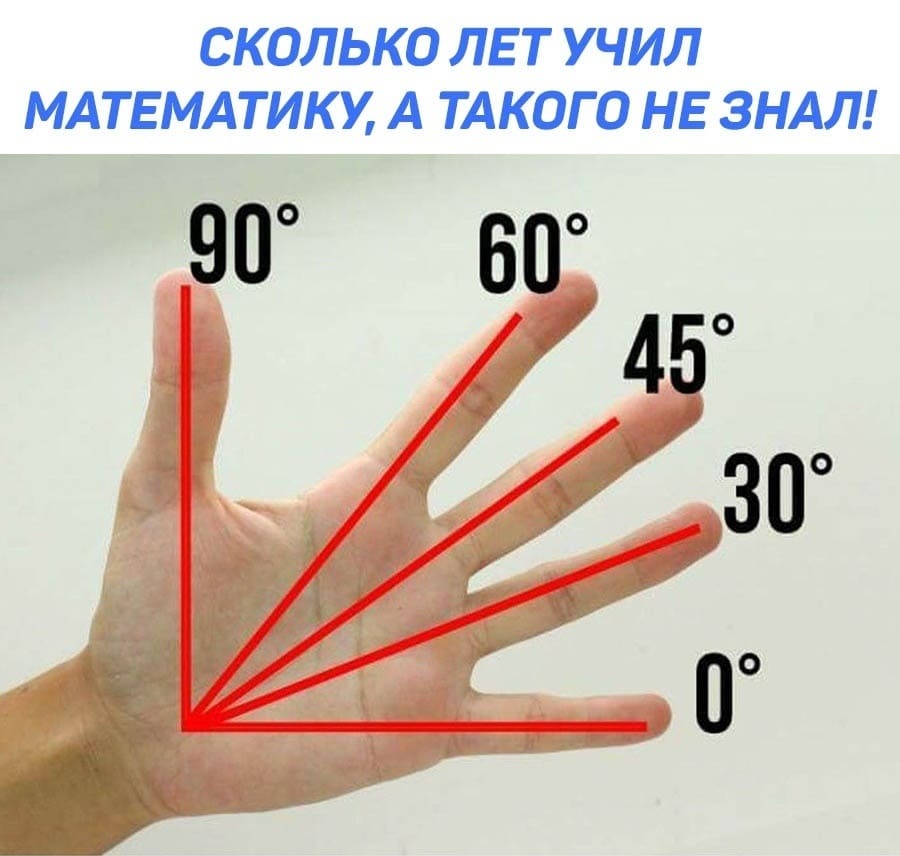
Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.
Градусы наглядные: как их определить с помощью своей ладони
Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!
Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…
Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.
А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.
Но не только об этом хотелось сказать, глядя на рисунок…
Градусы стихотворные и число «пи»
Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.
Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:
Кто и шутя, и скоро пожелаетъ
Пи узнать число — ужъ знаетъ
Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».
Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.
Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.
Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».
Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?
Градусы боевые: почему наши деды победили
Штурман откладывает карту в сторону. Достает маневренный планшет. Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.
Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.
Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.
А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!
Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!
Градусы электрические: отклонение между напряжением и током
Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.
Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.
Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.
Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.
Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!
Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.
Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.
И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…
Градусы драматические: косинус 90 градусов равен нулю
А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!
Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.
Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.
Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.
Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.
Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.
Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…
Градусы из радиоточки
Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.
«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.
Пришло оно к нам из того самого электротехнического «косинуса фи».
Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…
Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.
Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «. два тире один». Это про «наши» градусы, про «косинус фи»!
Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.
Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.
А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.
Градусы музыкальные
Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!
Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли:
Почему пи равно 180 градусов
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )
В предыдущем уроке мы освоили отсчёт углов на тригонометрическом круге. Узнали, как отсчитывать положительные и отрицательные углы. Осознали, как нарисовать угол больше 360 градусов. Пришла пора разобраться с измерением углов. Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да.
Стандартные задания по тригонометрии с числом «Пи» решаются неплохо. Зрительная память выручает. А вот любое отклонение от шаблона – валит наповал! Чтобы не свалиться – понимать надо. Что мы с успехом сейчас и сделаем. В смысле – всё поймём!
Итак, в чём считаются углы? В школьном курсе тригонометрии используются две меры: градусная мера угла и радианная мера угла. Разберём эти меры. Без этого в тригонометрии – никуда.
Градусная мера угла.
К градусам мы как-то привыкли. Геометрию худо-бедно проходили. Да и в жизни частенько встречаемся с фразой «повернул на 180 градусов», например. Градус, короче, штука простая.
Да? Ответьте мне тогда, что такое градус? Что, не получается с ходу? То-то.
Градусы придумали в Древнем Вавилоне. Давненько это было. Веков 40 назад. И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус – это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее. Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак. Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно. Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя. В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили, конечно. Примерно. В 3,1415926. раз.
Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой – бесконечное число цифр без всякого порядка. Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой. Запоминаем:
Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:
Где L – длина окружности, а d – её диаметр.
В геометрии пригодится.
Для общего образования добавлю, что число «Пи» сидит не только в геометрии. В самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно! Само по себе. Вне наших желаний. Вот так.
Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? Нет? Ну ладно. Выскажу версию. У древних вавилонян не спросишь. Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие – 360? И в каком варианте этих делителей нацело – больше? Людям такое деление очень удобно. Но.
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся. Высшая математика – дама серьёзная, по законам природы устроена. И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245. И что мне делать? Нет уж. » Пришлось послушаться. Природу не обманешь.
Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь – радиан!
Радианная мера угла.
Что такое радиан? В основе определения радиана – всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса (R). Смотрим картинки.
Будем считать, что этот малюсенький угол имеет величину 1 градус:
Маленький такой угол, почти и нет его. Наводим курсор на картинку (или коснёмся картинки на планшете) и видим примерно один радиан. L = R
Один радиан много больше одного градуса. А во сколько раз?
Смотрим следующую картинку. На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
А теперь я нарежу этот полукруг радианами! Наводим курсор на картинку и видим, что в 180° укладывается 3 с хвостиком радиана.
Кто угадает, чему равен этот хвостик!?
Да! Этот хвостик – 0,1415926. Здравствуй, число «Пи», мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926. радиан. Как вы сами понимаете, всё время писать 3,1415926. неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
А вот в Интернете число
писать неудобно. Поэтому я в тексте пишу его по имени – «Пи». Не запутаетесь, поди.
Вот теперь совершенно осмысленно можно записать приближённое равенство:
Или точное равенство:
Определим, сколько градусов в одном радиане. Как? Легко! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула – это тоже уравнение!) на 3,14:
Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
Но главное умение этой темы – перевод градусов в радианы и обратно.
Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан – 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан? Вот и пишем:
Или, более экзотическое выражение:
Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула – это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут. Получаем, что один градус равен:
Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:
Как видите, в неспешной беседе с лирическими отступлениями выяснилось, что радианы – это очень просто. Да и перевод без проблем. И «Пи» – вполне терпимая штука. Так откуда путаница!?
Вскрою тайну. Дело в том, что в тригонометрических функциях значок градусов – пишется. Всегда. Например, sin35°. Это синус 35 градусов. А значок радианов (рад) – не пишется! Он подразумевается. То ли лень математиков обуяла, то ли ещё что. Но решили не писать. Если внутри синуса – котангенса нет никаких значков, то угол – в радианах! Например, cos3 – это косинус трёх радианов.
Это и приводит к непоняткам. Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры – стандартные. Но «Пи» – это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!
Ещё раз: «Пи» – это число! 3,14. Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся.
«Пи» – это число! Что, достал я вас этой фразой? Вы уже всё давно поняли? Ну ладно. Проверим. Скажите-ка, какое число больше?
Это из серии слегка нестандартных вопросов, которые могут и в ступор вогнать.
Если вы тоже в ступор впали, вспоминаем заклинание: «Пи» – это число! 3,14. В самом первом синусе четко указано, что угол – в градусах! Стало быть, заменять «Пи» на 180° – нельзя! «Пи» градусов – это примерно 3,14°. Следовательно, можно записать:
Во втором синусе обозначений никаких нет. Значит, там – радианы! Вот здесь замена «Пи» на 180° вполне прокатит. Переводим радианы в градусы, как написано выше, получаем:
Осталось сравнить эти два синуса. Что. забыли, как? С помощью тригонометрического круга, конечно! Рисуем круг, рисуем примерные углы в 60° и 1,05°. Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05°.
Совершенно аналогично поступим и с косинусами. На круге нарисуем углы примерно 4 градуса и 4 радиана (не забыли, чему примерно равен 1 радиан?). Круг всё и скажет! Конечно, cos4 меньше cos4°.
Потренируемся в обращении с мерами угла.
Переведите эти углы из градусной меры в радианную:
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
У вас должны получиться такие значения в радианах (в другом порядке!)
 |  |  |  |
 |  |  |
Я, между прочим, специально выделил ответы в две строчки. Ну-ка, сообразим, что за углы в первой строчке? Хоть в градусах, хоть в радианах?
Да! Это оси системы координат! Если смотреть по тригонометрическому кругу, то подвижная сторона угла при этих значениях точно попадает на оси. Эти значения нужно знать железно. И угол 0 градусов (0 радиан) я отметил не зря. А то некоторые этот угол никак на круге найти не могут. И, соответственно, в тригонометрических функциях нуля путаются. Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге – сплошь и рядом.
Во второй строчке – тоже углы специальные. Это 30°, 45° и 60°. И что в них такого специального? Особо – ничего. Единственное отличие этих углов от всех остальных – именно про эти углы вы должны знать всё. И где они располагаются, и какие у этих углов тригонометрические функции. Скажем, значение sin100° вы знать не обязаны. А sin45° – уж будьте любезны! Это обязательные знания, без которых в тригонометрии делать нечего. Но об этом подробнее – в следующем уроке.
А пока продолжим тренировку. Переведите эти углы из радианной меры в градусную:
 |  |  |  |  |  |  |  |  |
У вас должны получиться такие результаты (в беспорядке):
210°; 150°; 135°; 120°; 330°; 315°; 300°; 240°; 225°.
Получилось? Тогда можно считать, что перевод градусов в радианы и обратно – уже не ваша проблема.) Но перевод углов – это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже.
Второй мощный шаг – это умение определять положение любого угла на тригонометрическом круге. И в градусах, и в радианах. Про это самое умение я буду вам во всей тригонометрии занудно намекать, да. ) Если вы всё знаете (или думаете, что всё знаете) про тригонометрический круг, и отсчёт углов на тригонометрическом круге, можете провериться. Решите эти несложные задания:
1. В какую четверть попадают углы:
2. В какую четверть попадают углы:
Тоже без проблем? Ну, смотрите. )
3. Сможете разместить по четвертям углы:
Смогли? Ну вы даёте..)
4. На какие оси попадёт уголок:
5. В какую четверть попадают углы:
И это получилось!? Ну, тогда я прям не знаю. )
6. Определить, в какую четверть попадают углы:
1, 2, 3 и 20 радианов.
Ответ дам только на последний вопрос (он слегка хитрый) последнего задания. Угол в 20 радианов попадёт в первую четверть.
Остальные ответы не дам не из жадности.) Просто, если вы не решили чего-то, сомневаетесь в результате, или на задание №4 потратили больше 10 секунд, вы слабо ориентируетесь в круге. Это будет вашей проблемой во всей тригонометрии. Лучше от неё (проблемы, а не тригонометрии!)) избавиться сразу. Это можно сделать в теме: Практическая работа с тригонометрическим кругом в разделе 555.
Там рассказано, как просто и правильно решать такие задания. Ну и эти задания решены, разумеется. И четвёртое задание решено за 10 секунд. Да так решено, что любой сможет!
Если же вы абсолютно уверены в своих ответах и вас не интересуют простые и безотказные способы работы с радианами – можете не посещать 555. Не настаиваю.)
Хорошее понимание – достаточно веская причина, чтобы двигаться дальше!)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся – с интересом!)
А вот здесь можно познакомиться с функциями и производными.
Здесь легко и интересно общаться. Присоединяйся!
на википедии почитай про число «пи», там все разжевано
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
Также можно выразить один градус в радианах.
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
Значит, в одном радиане примерно 57 градусов
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Применим формулу перехода от радианов к градусам и получим:
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.