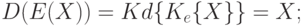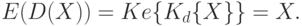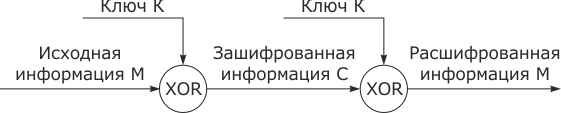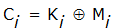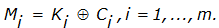Что следует делать для увеличения криптостойкости шифра
Б) набор данных, заверенных печатью центра сертификации, и включающий открытый ключ, список дополнительных атрибутов, принадлежащих абоненту, и предназначение открытого ключа;
В) набор данных, заверенных цифровой подписью центра сертификации, и включающий открытый ключ и список дополнительных атрибутов, принадлежащих абоненту.
33. Что означает термин мощность алфавита?
А) количество символов в открытом алфавите;
Б) число возможных комбинаций символов открытого алфавита;
В) количество шифрвеличин открытого алфавита.
34. К какому классу шифров относится шифр, если фрагмент открытого текста (отдельные буквы или группа букв) заменяются некоторыми их эквивалентами (буквами, цифрами, символами или их комбинацией) в шифртексте?
Б) шифры перестановки;
В) композиционные шифры.
35. К какому классу шифров относится шифр, если буквы открытого текста при шифровании каким-нибудь способом перестанавливаются, то есть изменяется только порядок следования символов открытого текста?
Б) шифры перестановки;
В) композиционные шифры.
36. Что следует делать для увеличения криптостойкости шифра?
А) увеличивать разницу между числом шифрвеличин и числом букв в алфавите;
Б) более равномерной должна быть диаграмма повторяемости знаков шифртекста;
В) оба ответа правильны.
37. Для чего используются блочные шифры?
А) для увеличения количества шифрвеличин;
Б) для увеличения скорости шифрования;
В) оба ответа правильны.
38. В чем состоит основное преимущество асимметричного шифрования?
А) нет необходимости в передаче секретного ключа, который может быть перехвачен злоумышленником;
Б) большая трудоемкость симметричного шифрования и, как результат, меньшие скорости при шифровании;
В) оба ответа верны.
39. Какие шифры называются омофонами?
А) шифры многозначной замены;
Б) многоалфавитные шифры;
В) шифры гаммирования.
40. Что такое шифрвеличина?
А) число возможных эквивалентов для замены открытых символов;
Б) эквиваленты в шифртексте, заменяющие символы или группы символов в открытого текста;
В) открытый текст предварительно представляется в виде последовательности «подслов», называемых шифрвеличинами.
41. С какими целями в криптографии вводятся модели открытых текстов??
А) служат основой для автоматизации процессов криптоанализа шифртекстов;
Б) служат основой в процессе изучения криптостойкости различных систем шифрования;
В) оба ответа верны.
42. К какому классу шифров относятся аддитивные методы шифрования?
Б) шифры многозначной замены;
В) шифры гаммирования.
43. К какому классу шифров относятся аналитические способы шифрования?
Б) шифры перестановки;
В) маршрутные перестановки.
44. Какие из приведенных шифров являются шифрами перестановки?
45. Какие из приведенных шифров являются шифрами замены?
46. Какие свойства открытого текста используются при вскрытии шифра перестановки?
А) ограничением может послужить появление запретных биграмм;
Б) наиболее частые биграммы открытого текста, которые можно составить из букв рассматриваемого шифрованного текста;
В) оба ответа верны.
47. Какая из математических моделей соответствует алгоритму шифра Атбаш?
48. Зашифруйте с помощью матричного шифра с ключевой матрицей 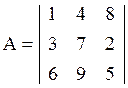
49. Что более целесообразно для надежной защиты информации?
А) архивация открытого текста с последующим;
Б) шифрование открытого текста с последующей архивацией;
В) не имеет значения.
50. К каким шифрам относится система шифрования Петра I «Цифирь»?
Б) шифры биграммной замены;
В) шифры простой замены.
51. На каком способе шифрования был основан биграммный шифр Плэйфера (Playfair, Великобритания), применявшийся Великобританией во время Первой мировой воны?
Простые криптосистемы
Криптографические методы являются наиболее эффективными средствами защиты информации в автоматизированных системах (АС). А при передаче информации по протяженным линиям связи они являются единственным реальным средством предотвращения несанкционированного доступа.
Основные требования к криптографическому закрытию информации в АС
Классификация основных методов криптографического закрытия информации
Шифрование методом замены (подстановки)
Наиболее простой метод шифрования. Символы шифруемого текста заменяются другими символами, взятыми из одного алфавита (одноалфавитная замена) или нескольких алфавитов (многоалфавитная подстановка).
Одноалфавитная подстановка
Примеры таблиц замены:
Стойкость метода простой замены низкая. Зашифрованный текст имеет те же самые статистические характеристики, что и исходный, поэтому зная стандартные частоты появления символов в том языке, на котором написано сообщение, и подбирая по частотам появления символы в зашифрованном сообщении, можно восстановить таблицу замены. Для этого требуется лишь достаточно длинный зашифрованный текст, для того, чтобы получить достоверные оценки частот появления символов. Поэтому простую замену используют лишь в том случае, когда шифруемое сообщение достаточно коротко!
Многоалфавитная замена повышает стойкость шифра.
Многоалфавитная одноконтурная обыкновенная подстановка
Таблица Вижинера для русского алфавита:
При шифровании и дешифровании нет необходимости держать в памяти всю матрицу Вижинера, поскольку используя свойства циклического сдвига, можно легко вычислить любую строку матрицы по ее номеру и первой строке.
Используя свойства циклического сдвига влево элементы k-ой строки можно выразить через элементы первой строки
При дешифровании производится обратная замена
Таким образом при дешифровании по k-ой строке матрицы Вижинера символа из зашифрованного текста, значение которого равно a(1,j), проводится обратная подстановка
Многоалфавитная одноконтурная монофоническая подстановка
В монофонической подстановке количество и состав алфавитов выбирается таким образом, чтобы частоты появления всех символов в зашифрованном тексте были одинаковыми. При таком положении затрудняется криптоанализ зашифрованного текста с помощью его статистической обработки. Выравнивание частот появления символов достигается за счет того, что для часто встречающихся символов исходного текста предусматривается большее число заменяющих символов, чем для редко встречающихся.
Пример таблицы монофонической замены:
Шифрование проводится так же, как и при простой подстановке, с той лишь разницей, что после шифрования каждого символа соответствующий ему столбец алфавитов циклически сдвигается вверх на одну позицию. Таким образом, столбцы алфавитов как бы образуют независимые друг от друга кольца, поворачиваемые вверх на один знак каждый раз после шифрования соответствующего знака исходного текста.
Многоалфавитная многоконтурная подстановка
Многоконтурная подстановка заключается в том, что для шифрования используются несколько наборов (контуров) алфавитов, используемых циклически, причем каждый контур в общем случае имеет свой индивидуальный период применения. Частным случаем многоконтурной полиалфавитной подстановки является замена по таблице Вижинера, если для шифрования используется несколько ключей, каждый из которых имеет свой период применения.
Общая модель шифрования подстановкой может быть представлена в следующем виде:
Шифрование методом перестановки
При шифровании перестановкой символы шифруемого текста переставляются по определенным правилам внутри шифруемого блока этого текста.
Простая перестановка
Выбирается размер блока шифрования в n столбцов и m строк и ключевая последовательность, которая формируется из натурального ряда чисел 1,2. n случайной перестановкой.
Например, зашифруем текст
блоком размером 8*3 и ключом 5-8-1-3-7-4-6-2.
Таблица простой перестановки будет иметь вид:
Ключ 5 8 1 3 7 4 6 2
Г Р У З И Т Е _ А П Е Л Ь С И Н Ы _ Б О Ч К А Х
Перестановка, усложненная по таблице
При усложнении перестановки по таблицам для повышения стойкости шифра в таблицу перестановки вводятся неиспользуемые клетки таблицы. Количество и расположение неиспользуемых элементов является дополнительным ключом шифрования.
Для дальнейшего увеличения криптостойкости шифра можно в процессе шифрования менять ключи, размеры таблицы перестановки, количество и расположение неиспользуемых элементов по некоторому алгоритму, причем этот алгоритм становится дополнительным ключом шифра.
Перестановка, усложненная по маршрутам
Высокую стойкость шифрования можно обеспечить усложнением перестановок по маршрутам типа гамильтоновских. При этом для записи символов шифруемого текста используются вершины некоторого гиперкуба, а знаки зашифрованного текста считываются по маршрутам Гамильтона, причем используются несколько различных маршрутов. Для примера рассмотрим шифрование по маршрутам Гамильтона при n=3.
Струкрура трехмерного гиперкуба:
Номера вершин куба определяют последовательность его заполнения символами шифруемого текста при формировании блока. В общем случае n-мерный гиперкуб имеет n 2 вершин.
Маршруты Гамильтона имеют вид:
Последовательность перестановок символов в шифруемом блоке для первой схемы 5-6-2-1-3-4-8-7, а для второй 5-1-3-4-2-6-8-7. Аналогично можно получить последовательность перестановок для других маршрутов: 5-7-3-1-2-6-8-4, 5-6-8-7-3-1-2-4, 5-1-2-4-3-7-8-6 и т.д.
Размерность гиперкуба, количество вид выбираемых маршрутов Гамильтона составляют секретный ключ метода.
Стойкость простой перестановки однозначно определяется размерами используемой матрицы перестановки. Например, при использовании матрицы 16*16 число возможных перестановок достигает 1.4E26. Такое число вариантов невозможно перебрать даже с использованием ЭВМ. Стойкость усложненных перестановок еще выше. Однако следует иметь в виду, что при шифровании перестановкой полностью сохраняются вероятностные характеристики исходного текста, что облегчает криптоанализ.
Шифрование методом гаммирования
Суть метода состоит в том, что символы шифруемого текста последовательно складываются с символами некоторой специальной последовательности, называемой гаммой. Иногда такой метод представляют как наложение гаммы на исходный текст, поэтому он получил название «гаммирование«.
Наложение гаммы можно осуществить несколькими способами, например по формуле
Расшифрование текста проводится по той же формуле:
Последовательность гаммы удобно формировать с помощью датчика псевдослучайных чисел (ПСЧ).
Стойкость гаммирования однозначно определяется длиной периода гаммы. При использовании современных ПСЧ реальным становится использование бесконечной гаммы, что приводит к бесконечной теоретической стойкости зашифрованного текста.
Шифрование с помощью аналитических преобразований
В качестве ключа задается квадратная матрица ||a|| размера n*n. Исходный текст разбивается на блоки длиной n символов. Каждый блок рассматривается как n-мерный вектор. А процесс шифрования блока заключается в получении нового n-мерного вектора (зашифрованного блока) как результата умножения матрицы ||a|| на исходный вектор.
Расшифрование текста происходит с помощью такого же преобразования, только с помощью матрицы, обратной ||a||. Очевидно, что ключевая матрица ||a|| должна быть невырожденной.
Комбинированные методы шифрования
Достаточно эффективным средством повышения стойкости шифрования является комбинированное использование нескольких различных способов шифрования, т.е. последовательное шифрование исходного текста с помощью двух или более методов.
Стойкость комбинированного шифрования S не ниже произведения стойкостей используемых способов
Если какой-либо способ шифрования при независимом применении может обеспечить стойкость не ниже S, то комбинировать его с другими способами целесообразно лишь при выполнении условия
Организационные проблемы криптозащиты
Рассмотренные значения стойкости шифров являются потенциальными величинами. Они могут быть реализованы при строгом соблюдении правил использования криптографических средств защиты.
Под дублированием здесь понимается повторное шифрование одного и того же отрывка текста с использованием тех же ключей (например, если при первом шифровании произошел сбой). Нарушение этого правила резко снижает надежность шифрования, так как исходный текст может быть восстановлен с помощью статистического анализа двух вариантов зашифрованного текста.
Нельзя допускать злоумышленнику возможности направить в систему ряд специально подобранных сообщений и получать их в зашифрованном виде. Такого взлома не может выдержать ни одна криптосистема!
Важными аспектами организации криптозащиты являются выбор способа закрытия, распределение ключей и доставка их в места пользования (механизм распределения ключей).
Выбор способа защиты тесно связан с трудоемкостью метода шифрования, степенью секретности закрываемых данных, стойкостью метода и объемом шифруемой информации.
Криптографическая стойкость
Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять возможным атакам на него. Атакующие криптографический алгоритм используют методы криптоанализа. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов, недостижимого объёма перехваченных открытых и зашифрованных сообщений или же такого времени раскрытия, что по его истечению защищенная информация будет уже не актуальна, и т. д.
Содержание
Типы криптостойких систем шифрования [ ]
Абсолютно стойкие системы [ ]
Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено К. Шенноном и опубликовано в работе «Теория связи в секретных системах». Там же определены требования к такого рода системам:
Стойкость этих систем не зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическое применение систем, удовлетворяющих требованиям абсолютной стойкости, ограничено соображениями стоимости и удобства пользования.
Некоторыми аналитиками утверждается, что Шифр Вернама является одновременно абсолютно криптографически стойким и к тому же единственным шифром, который удовлетворяет этому условию.
Достаточно стойкие системы [ ]
В основном применяются практически стойкие или вычислительно стойкие системы. Стойкость этих систем зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическая стойкость таких систем базируется на теории сложности и оценивается исключительно на какой-то определенный момент времени и последовательно c двух позиций:
В каждом конкретном случае могут существовать дополнительные критерии оценки стойкости.
Оценка криптостойкости систем шифрования [ ]
Начальная оценка [ ]
Текущая оценка [ ]
Дальнейшее исследование алгоритма с целью поиска слабостей (уязвимостей) (криптоанализ) добавляет оценки стойкости по отношению к известным криптографическим атакам (Линейный криптоанализ, дифференциальный криптоанализ и более специфические) и могут понизить известную стойкость.
Важность длительной проверки и открытого обсуждения [ ]
Чем более длительным и экспертным является анализ алгоритма и реализаций, тем более достоверной можно считать его стойкость. В нескольких случаях длительный и внимательный анализ приводил к снижению оценки стойкости ниже приемлемого уровня (например, в черновых версиях FEAL). Недостаточная проверка (по мнению многих криптографов — искусственное ослабление) алгоритма потокового шифрования A5/1 привела к успешной атаке (см…).
Методы защиты информации в компьютерных системах и сетях
3.4. Криптографические методы защиты
3.4.1. Основные термины и определения
Современная криптография включает в себя следующие основные разделы:
Введем некоторые понятия, необходимые в дальнейшем:
| алфавит | — | конечное множество используемых для шифрования информации знаков; |
| текст | — | упорядоченный набор из элементов алфавита; |
| шифр | — | совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, заданных алгоритмом криптографического преобразования (криптоалгоритмом); |
| ключ | — | сменный элемент шифра, применяемый для закрытия отдельного сообщения, т.е. конкретное секретное состояние параметров криптоалгоритма, обеспечивающее выбор одного варианта преобразования из совокупности возможных; именно ключом определяется в первую очередь безопасность защищаемой информации и поэтому применяемые в надежных шифрах преобразования в большой степени зависят от ключа; |
| зашифрование | — | преобразование открытых данных в закрытые (зашифрованные) с помощью определенных правил, содержащихся в шифре; |
| расшифрование | — | обратный процесс; |
| шифрование | — | процесс зашифрования или расшифрования; |
| криптосистема | — | состоит из пространства ключей, пространства открытых текстов, пространства шифротекстов и алгоритмов зашифрования и расшифрования; |
| дешифрование | — | процесс преобразования закрытых данных в открытые при неизвестном ключе и (или) неизвестном алгоритме (вскрытие или взлом шифра); |
| синхропосылка | — | исходные параметры криптоалгоритма; |
| раскрытие криптоалгоритма | — | результат работы криптоаналитика, приводящий к возможности эффективного определения любого зашифрованного с помощью данного алгоритма открытого текста; |
| стойкость криптоалгоритма | — | способность шифра противостоять всевозможным попыткам его раскрытия, т.е. атакам на него. |
3.4.2. Оценка надежности криптоалгоритмов
Все современные шифры базируются на принципе Кирхгофа, согласно которому секретность шифра обеспечивается секретностью ключа, а не секретностью алгоритма шифрования. В некоторых ситуациях (например, в военных, разведывательных и дипломатических ведомствах) нет никаких причин делать общедоступным описание сути криптосистемы. Сохраняя такую информацию в тайне, можно дополнительно повысить надежность шифра. Однако полагаться на секретность этой информации не следует, так как рано или поздно она будет скомпрометирована. Поэтому анализ надежности таких систем всегда должен проводиться исходя из того, что противник имеет всю информацию о применяемом криптоалгоритме, ему неизвестен только реально использованный ключ. В связи с вышеизложенным можно сформулировать общее правило: при создании или при анализе стойкости криптосистем не следует недооценивать возможностей противника. Их лучше переоценить, чем недооценить.
Методы оценки качества криптоалгоритмов, используемые на практике:
В первом случае многое зависит от квалификации, опыта, интуиции криптоаналитиков и от правильной оценки возможностей противника. Обычно считается, что противник знает шифр, имеет возможность его изучения, знает некоторые характеристики открытых защищаемых данных, например тематику сообщений, их стиль, стандарты, форматы и т.п.
Во втором случае оценку стойкости шифра заменяют оценкой минимальной сложности алгоритма его вскрытия. Однако получение строгих доказуемых оценок нижней границы сложности алгоритмов рассматриваемого типа проблематично. Иными словами, всегда возможна ситуация, когда алгоритм вскрытия шифра, сложность которого анализируется, оказывается вовсе не самым эффективным.
Сложность вычислительных алгоритмов можно оценивать числом выполняемых элементарных операций, при этом необходимо учитывать их стоимость и затраты на их выполнение. В общем случае это число должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютерных систем. Качественный шифр невозможно раскрыть способом более эффективным, нежели полный перебор по всему ключевому пространству, при этом криптограф должен рассчитывать только на то, что у противника не хватит времени и ресурсов, чтобы это сделать.
В третьем случае можно сформулировать следующие необходимые условия стойкости криптосистемы, проверяемые статистическими методами:
Существует много различных криптоалгоритмов, при этом нет ни одного, подходящего для всех случаев. В каждой конкретной ситуации выбор криптоалгоритма определяется следующими факторами:
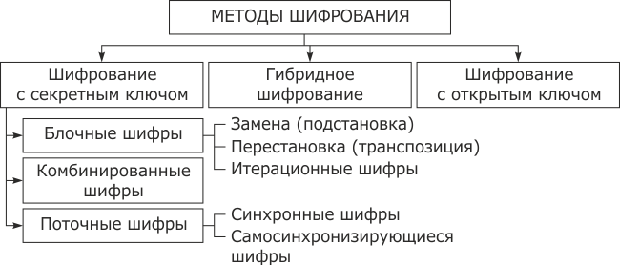
3.4.3. Классификация методов шифрования информации
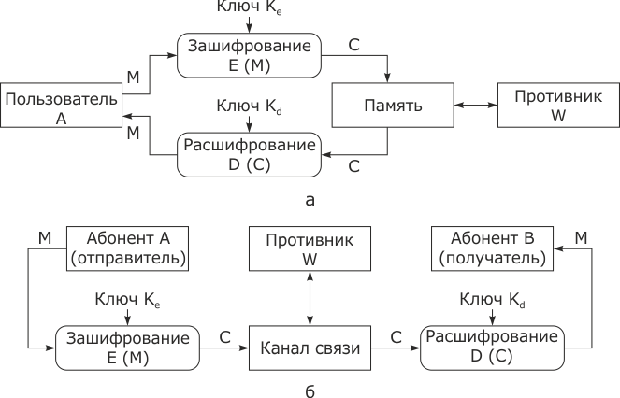
Процедуры зашифрования E (encryption) и расшифрования D (decryption) можно представить в следующем виде:
| где | M (message) и C (ciphertext) | — | открытый и зашифрованный тексты; |
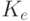 и и 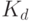 | — | ключи зашифрования и расшифрования. |
Функции за- и расшифрования взаимно обратные, иначе говоря, для любого текста X справедливо:
На рис. 3.5 приведена классификация методов шифрования информации. Различают два типа алгоритмов шифрования симметричные (с секретным ключом) и асимметричные (с открытым ключом). В первом случае обычно ключ расшифрования совпадает с ключом зашифрования, т.е.
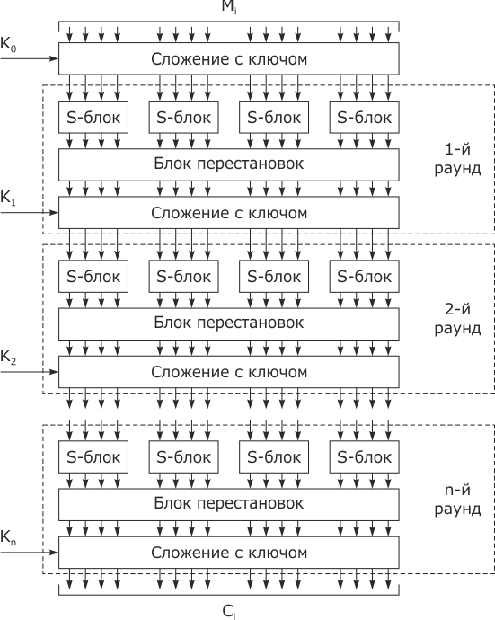
Блочные итерационные шифры. Принцип работы всех современных блочных шифров суть многократное повторение одной и той же раундовой операции. В некоторых случаях раундовые ключи получаются из ключа всей системы с помощью алгоритма выработки раундовых ключей (при этом размер ключа системы существенно меньше суммарного размера всех раундовых ключей).
Идея, лежащая в основе итерационных блочных шифров, состоит в построении криптостойкой системы путем многократного применения относительно простых криптографических преобразований, в качестве которых К. Шеннон предложил использовать преобразования замены (подстановки) (substitution) и перестановки (permutation); схемы, реализующие эти преобразования, называются SP-сетями. Действие таких шифров аналогично «алгоритму», к которому прибегают, когда месят тесто:
Многократное использование этих преобразований, приведенное на рис. 3.6, позволяет обеспечить два свойства, которые должны быть присущи стойким шифрам: рассеивание (diffusion) и перемешивание (confusion) информации.
Рассеивание и перемешивание предполагают:
Наличие у шифра этих свойств:
Интересно отметить, что в первоначальной схеме, предложенной IBM, все шестнадцать 48-разрядных раундовых ключей выбирались независимо, т.е. размер ключа был равен 768 битам. Однако по требованию Агентства национальной безопасности США (АНБ), во-первых, размер ключа был уменьшен до 64 бит, из которых только 56 являются секретными, во-вторых, в алгоритме определены перестановки лишь специального вида, не зависящие от ключа, что наводило критиков этого алгоритма на мысль, будто АНБ могла использовать известные ей слабости алгоритма для его взлома. На протяжении последних десятилетий DES подвергался интенсивному и всестороннему исследованию и по современным понятиям уже не считается надежным, в первую очередь из-за небольшой разрядности ключа.
Существует несколько предложений, направленных на усовершенствование DES. Наиболее известное из них, Triple DES, заключается в трехкратном применении алгоритма.
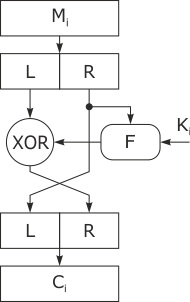
В качестве исходных данных раундовая функция шифрования ГОСТа получает 64-разрядный блок данных D = (L, R) и 32-разрядный раундовый ключ, в качестве которого используется один из элементов ключа Кi. В ходе выполнения преобразования левая L и правая R половины блока данных рассматриваются как отдельные 32-разрядные элементы данных, в качестве которых они подвергаются следующим преобразованиям:
Полученные значения элементов L и R выдаются в качестве результата шага раундового преобразования.
ГОСТ 28147-89 определяет три режима шифрования данных (простая замена, гаммирование и гаммирование с обратной связью) и режим выработки имитоприставки (кода аутентификации сообщений).
3.4.4. Абсолютно стойкий шифр. Гаммирование
Простейшей и в то же время наиболее надежной из всех схем шифрования является так называемая схема однократного использования, приведенная на рис. 3.8, изобретение которой чаще всего связывают с именем Г.С. Вернама.
| где |  , , 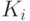 и и 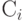 | — | очередной i-й бит соответственно исходного сообщения, ключа и зашифрованного сообщения; |
| m | — | число битов открытого текста. |
Процесс расшифрования сводится к повторной генерации ключевой последовательности и наложения ее на зашифрованные данные. Уравнение расшифрования имеет вид:
К. Шенноном доказано, что, если ключ является фрагментом истинно случайной двоичной последовательностью с равномерным законом распределения, причем его длина равна длине исходного сообщения, и используется этот ключ только один раз, после чего уничтожается, такой шифр является абсолютно стойким, его невозможно раскрыть, даже если криптоаналитик располагает неограниченным запасом времени и неограниченным набором вычислительных ресурсов. Действительно, противнику известно только зашифрованное сообщение С, при этом все различные ключевые последовательности K возможны и равновероятны, а значит, возможны и любые сообщения M, т.е. криптоалгоритм не дает никакой информации об открытом тексте.
Необходимые и достаточные условия абсолютной стойкости шифра:
Таким образом, построить эффективный криптоалгоритм можно, лишь отказавшись от абсолютной стойкости. Возникает задача разработки такого теоретически нестойкого шифра, для вскрытия которого противнику потребовалось бы выполнить такое число операций, которое осуществимо на современных и ожидаемых в ближайшей перспективе вычислительных средствах за разумное время. В первую очередь следует иметь схему, которая использует ключ небольшой разрядности, в дальнейшем выполняющий функцию «зародыша», порождающего значительно более длинную ключевую последовательность.
Данный результат может быть достигнут при использовании гаммирования, схема которого показана на рис. 3.9.
Гаммированием называют процедуру наложения на входную информационную последовательность гаммы шифра, т.е. последовательности с выходов генератора псевдослучайных последовательностей (ПСП) G. Последовательность называется псевдослучайной, если по своим статистическим свойствам она неотличима от истинно случайной последовательности, но в отличие от последней является детерминированной, т.е. знание алгоритма ее формирования дает возможность ее повторения необходимое число раз. Если символы входной информационной последовательности и гаммы представлены в двоичном виде, наложение чаще всего реализуется с помощью операции поразрядного сложения по модулю 2. Надежность шифрования методом гаммирования определяется качеством генератора гаммы.
3.4.5. Генераторы псевдослучайных последовательностей
Качественные ПСП, являясь по своей сути детерминированными, успешно заменяют во многих приложениях (в первую очередь связанных с защитой информации) случайные последовательности, которые чрезвычайно сложно формировать.
Можно выделить следующие задачи, требующие решения при организации защиты информационных систем:
Во всех рассмотренных случаях генераторы ПСП применяются либо непосредственно, либо косвенно, когда на их основе строятся генераторы случайных последовательностей, генераторы контрольных кодов и хеш-генераторы. Во всех случаях требуются последовательности с равномерным законом распределения.
Можно выделить следующие функции генераторов ПСП в системах защиты информации:
Требования к качественному генератору ПСП:
Непредсказуемость. Данное требование означает, что для противника, имеющего возможность анализировать фрагмент ПСП конечной длины, три задачи вычислительно неразрешимы:
Определенные статистические свойства. Это требование означает, что ни один из существующих статистических тестов не в состоянии обнаружить на выходе генератора какие-либо закономерности статистических зависимостей между различными последовательностями, формируемыми при инициализации генератора случайными значениями.
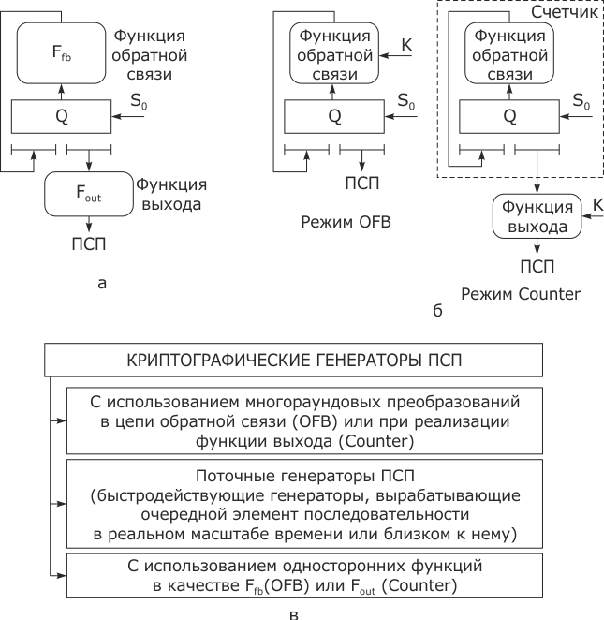
Принципы построения генераторов ПСП. Можно выделить два подхода при использовании в составе генераторов ПСП нелинейных функций: это использование нелинейной функции непосредственно в цепи обратной связи и двухступенчатая схема, в которой задача первой ступени (по сути счетчика) заключается всего лишь в обеспечении максимально большого периода при данном числе N элементов памяти Q. Во втором случае нелинейная функция является функцией выхода 
Вторую схему следует считать более предпочтительной, так как первая имеет следующие недостатки:
На рис. 3.10в показана классификация криптографических генераторов ПСП. Роль нелинейных функций 
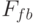
Наиболее обоснованными математически следует признать генераторы с использованием односторонних функций. Непредсказуемость данных генераторов основывается на сложности решения ряда математических задач (например, задачи дискретного логарифмирования или задачи разложения больших чисел на простые множители). Существенным недостатком генераторов этого класса является низкая производительность.
3.4.6. Поточные шифры
Шифр Вернама можно считать исторически первым поточным шифром. Так как поточные шифры в отличие от блочных осуществляют поэлементное шифрование потока данных без задержки в криптосистеме, их важнейшим достоинством является высокая скорость преобразования, соизмеримая со скоростью поступления входной информации. Таким образом обеспечивается шифрование практически в реальном масштабе времени вне зависимости от объема и разрядности потока преобразуемых данных.
В синхронных поточных шифрах (см. рис. 3.9) гамма формируется независимо от входной последовательности, каждый элемент (бит, символ, байт и т.п.) которой таким образом шифруется независимо от других элементов. В синхронных поточных шифрах отсутствует эффект размножения ошибок, т.е. число искаженных элементов в расшифрованной последовательности равно числу искаженных элементов зашифрованной последовательности, пришедшей из канала связи. Вставка или выпадение элемента зашифрованной последовательности недопустимы, так как из-за нарушения синхронизации это приведет к неправильному расшифрованию всех последующих элементов.