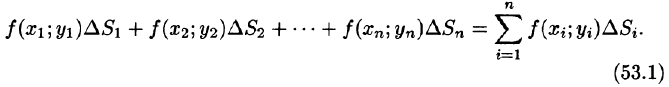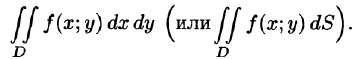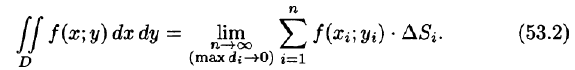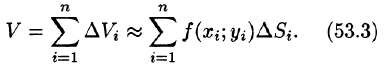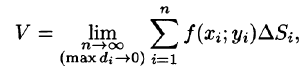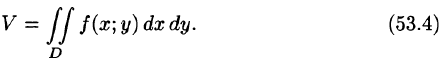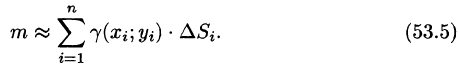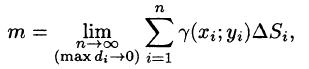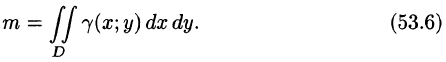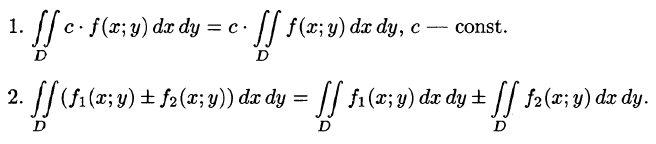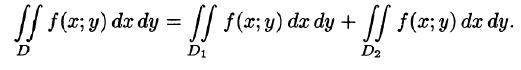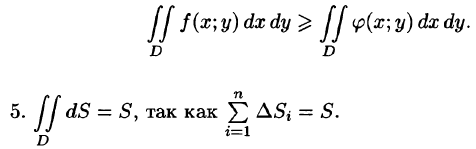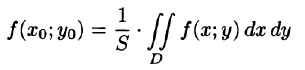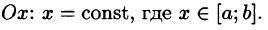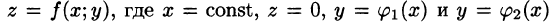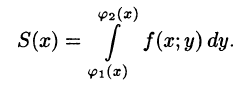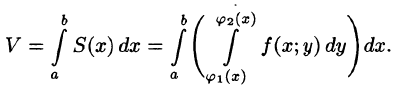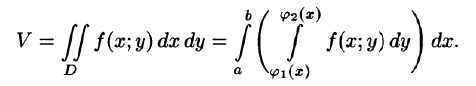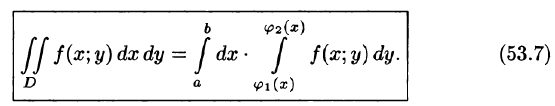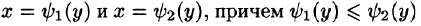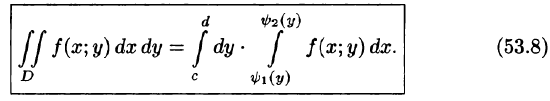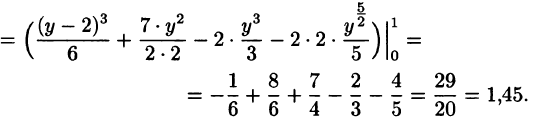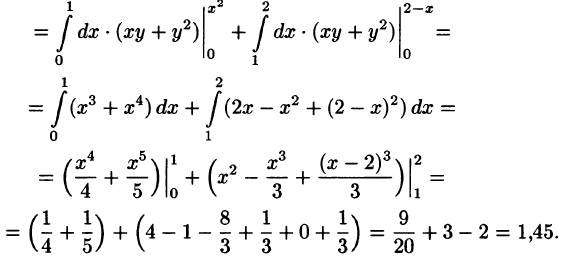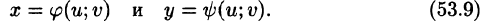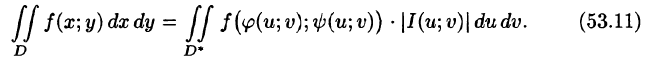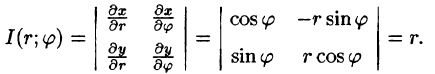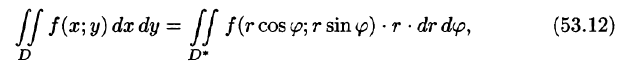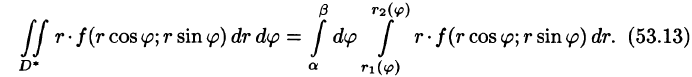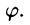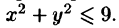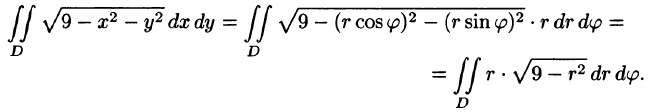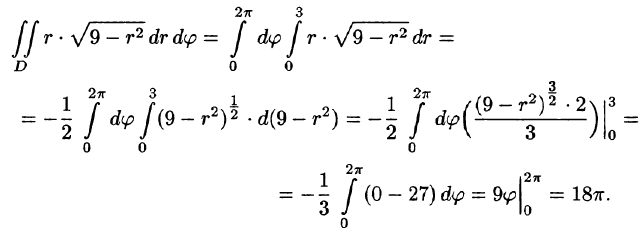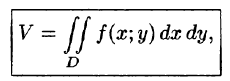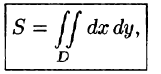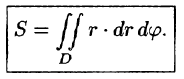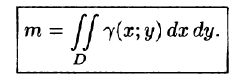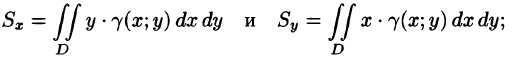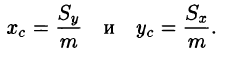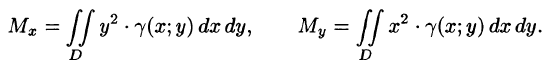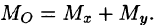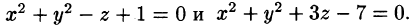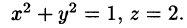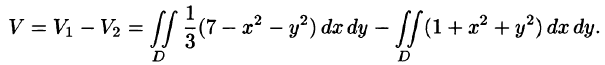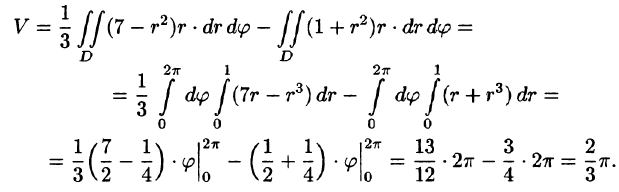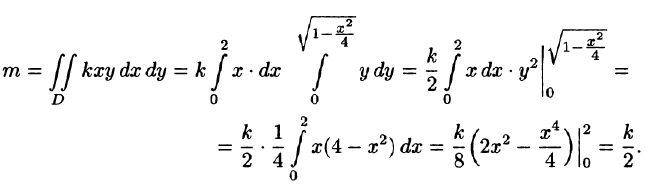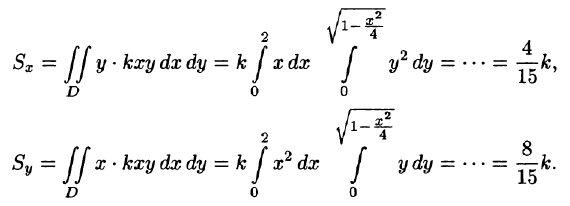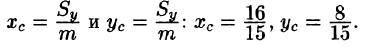Что считает двойной интеграл
Вычисление двойных интегралов: теория и примеры
Что значит вычислить двойной интеграл?
Записывается двойной интеграл так:

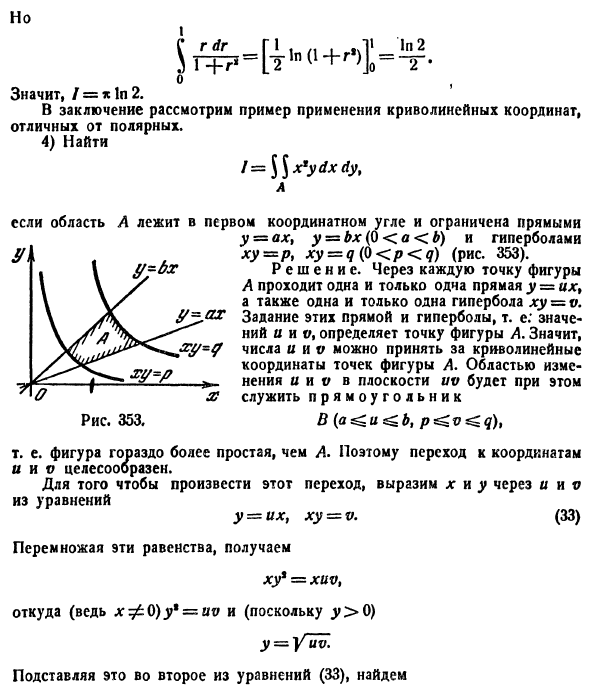
Случай прямоугольной области:
Случай криволинейной области:
Сведение двойного интеграла к повторному
Случай прямоугольной области
Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Пример 1. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случай криволинейной или треугольной области

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

Пример 3. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования и видим, что она треугольная:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:

Пример 4. Вычислить двойной интеграл


Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
Пример 5. Вычислить двойной интеграл

если область D ограничена прямыми

Пример 6. Вычислить двойной интеграл

если область D ограничена прямыми

x-правильная и неправильная, y-правильная и неправильная области интегрирования
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Вычисляется этот двойной интеграл так:
Смена порядка интегрирования
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Пример 8. Сменить порядок интегрирования для повторного интеграла



Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла

Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для 
Для 
Для 
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:

Вычисление площади и объёма с помощью двойных интегралов
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Расставляя пределы интегрирования, получаем следующий повторный интеграл:

Вычисляем внутренний (правый) интеграл:

Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
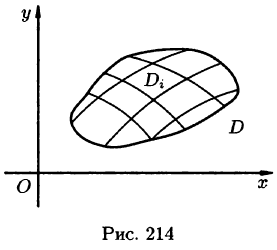
Так что же такое двойной интеграл?

которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
Двойной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой облас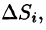
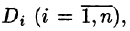
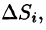
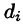
В каждой области 
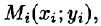
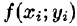
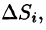
Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 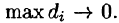
Таким образом, двойной интеграл определяется равенством
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
Геометрический и физический смысл двойного интеграла
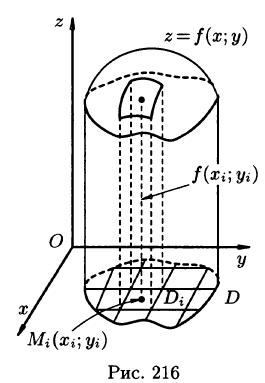
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью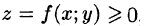

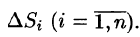

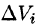
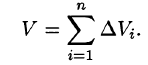
Возьмем на каждой площадке Di произвольную точку 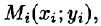

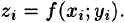
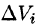
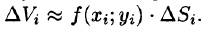
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» 

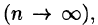
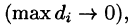
или, согласно равенству (53.2),
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 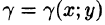
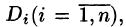
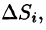

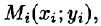
Если области D, достаточно малы, то плотность в каждой точке 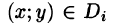
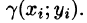

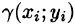
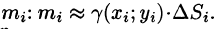
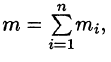
Точное значение массы получим как предел суммы (53.5) при условии
или, согласно равенству (53.2),
Итак, двойной интеграл от функции 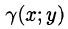
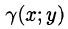
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
3.Если область D разбить линией на две области 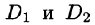
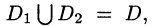
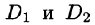
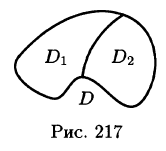
4.Если в области D имеет место неравенство 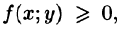
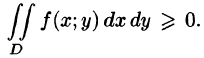
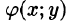
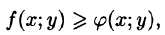
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 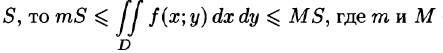
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка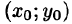
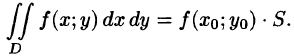
называют средним значением функции f(x; у) в области D.
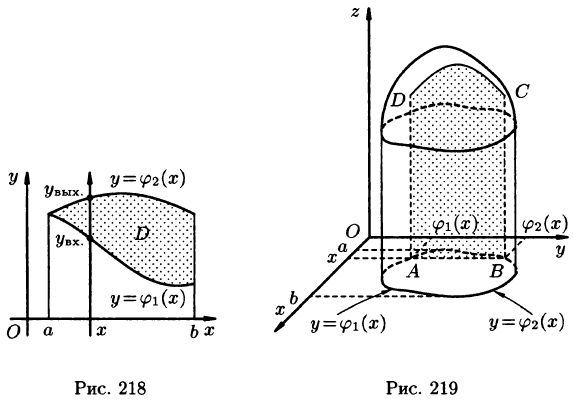
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 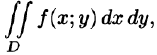
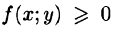
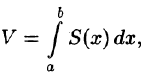
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми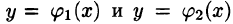
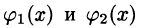
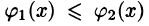
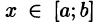
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
Площадь S(x) этой трапеции находим с помощью определенного интеграла
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 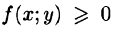
Это равенство обычно записывается в виде
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 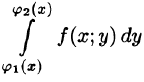
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 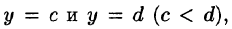
для всех 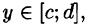
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
Пример:
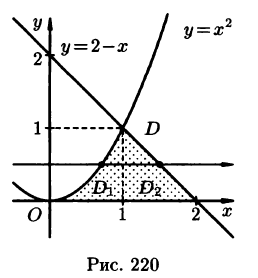
Вычислить 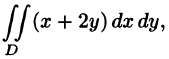
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
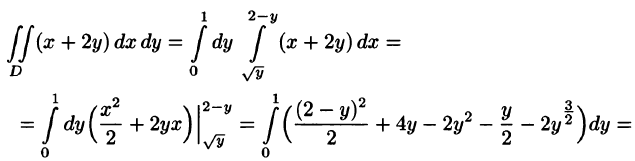
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 
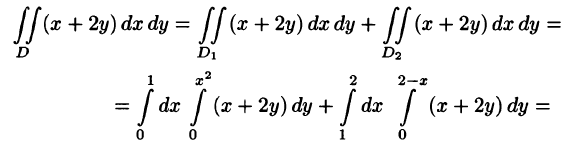
Ответ, разумеется, один и тот же.
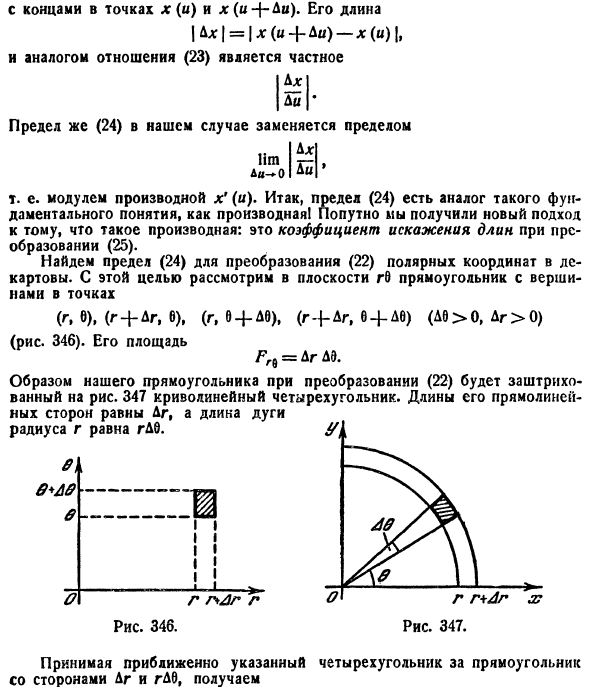
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами
В качестве инь возьмем полярные координаты 
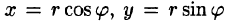
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
Формула замены переменных (53.11) принимает вид:
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами 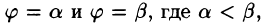
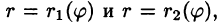
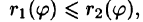
Внутренний интеграл берется при постоянном
Замечания:
Пример:
Вычислить 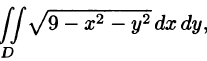
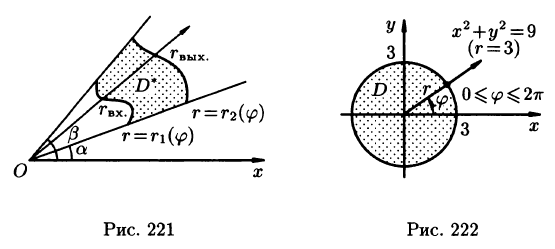
Решение: Применив формулу (53.12), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 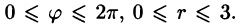
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 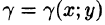
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
а координаты центра масс фигуры по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 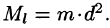
Момент инерции фигуры относительно начала координат — по формуле
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
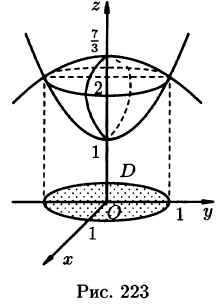
Пример:
Найти объем тела, ограниченного поверхностями
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
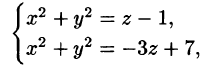
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 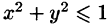
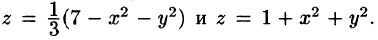
Переходя к полярным координатам, находим:
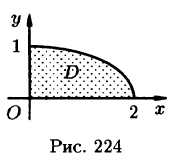
Пример:
Найти массу, статические моменты 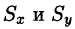
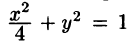
Решение: По формуле (53.6) находим массу пластинки. По условию, 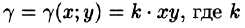
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
Двойной интеграл













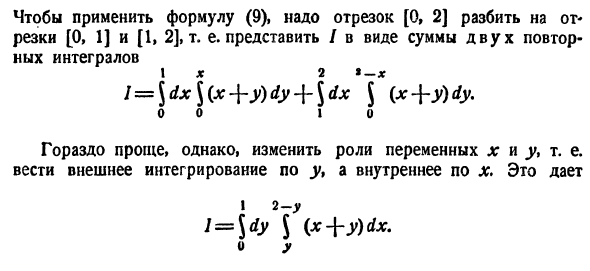















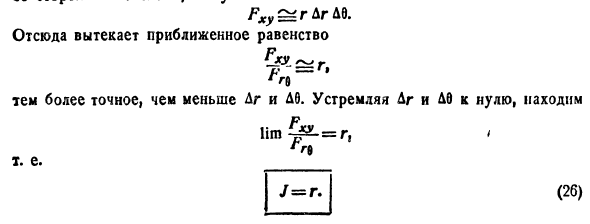


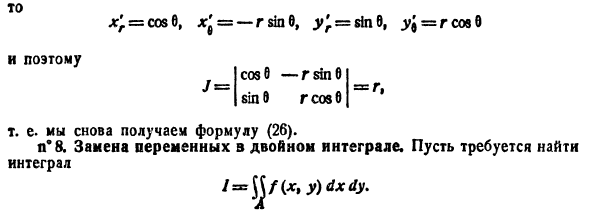

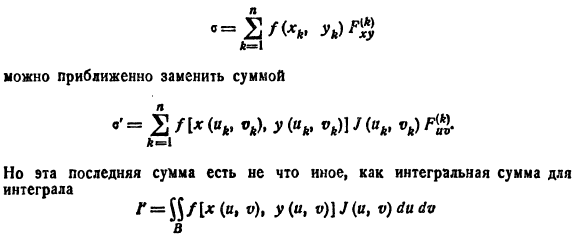



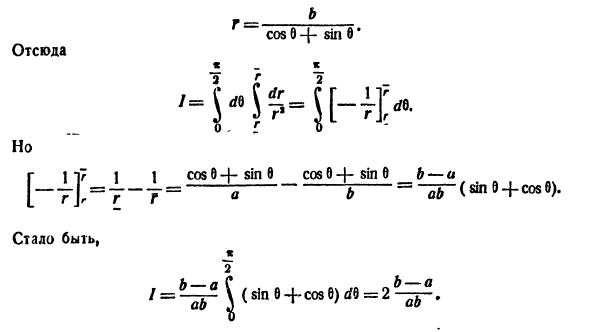

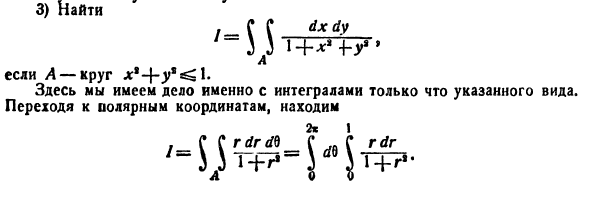




Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института