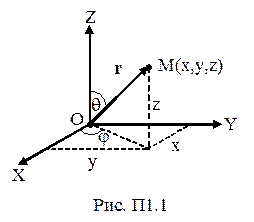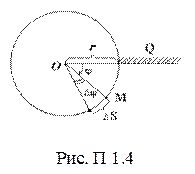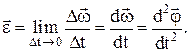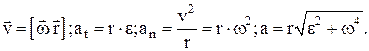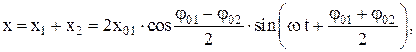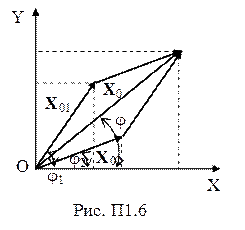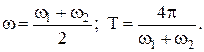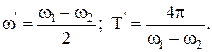Что изучает кинематика и динамика

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

1. Кинематика и динамика

1. Кинематика и динамика

В этой небольшой главе мы отнюдь не собираемся делать какого-либо, даже краткого, обзора принципов классической механики и, тем более, критически анализировать эту область физики. Для этого недостаточно было бы и целой книги; к тому же эти вопросы уже рассмотрены многими выдающимися учеными. Мы остановимся здесь лишь на некоторых вопросах, которые, на наш взгляд, представляют интерес в связи с излагаемым материалом.

Аналитическая механика состоит из двух разделов, носящих совершенно различный характер: кинематики и динамики, частным случаем которой является статика. Необходимо вкратце остановиться на этом разделении, поскольку оно основывается на предположениях, не оправдавших себя с точки зрения квантовой теории.

В самом деле, что же такое кинематика и почему ее изучают обычно прежде, чем динамику? Кинематика изучает движения тел, происходящие в трехмерном пространстве в течение какого-то времени и совершенно независимо от физических причин этого движения. На первый взгляд кажется вполне естественным предпослать изучению динамики изучение кинематики, ибо представляется совершенно логичным сначала изучить in abstracto различные виды движения в пространстве, а уж затем задаваться вопросом, по какой причине и следуя каким законам то или иное движение возникает в тех или иных условиях. Но этот кажущийся естественным путь в действительности покоится на одной гипотезе, в чем до последнего времени не отдавали себе ясного отчета даже наиболее выдающиеся умы. Действительно, математики, очевидно, вправе заниматься изучением перемещений в пространстве трех измерений в зависимости от параметра, который может быть идентифицирован со временем. Однако речь здесь идет о том, можно ли, как это без всякого анализа предполагалось, применять результаты этого абстрактного изучения к случаю реального движения физических объектов.

Классический переход от кинематики к динамике, по существу, содержит в себе гипотезу о том, что локализация физических объектов в некоторой абстрактной области трехмерного пространства и времени возможна вне зависимости от внутренних свойств самих физических объектов, например от их массы. Совершенно достоверно известно, что если оставаться в пределах нашего масштаба, то окружающие нас материальные тела с большой степенью точности могут считаться локализованными в пространстве и во времени. Именно это свойство тел и, в частности твердых, позволяет нам наглядно представить себе трехмерное пространство, в котором они перемещаются. Движение этих тел дает нам возможность точно определить время и способ его измерения. По этому оказывается вполне естественным, что методы аналитической механики с успехом применяют для изучения движения подобного рода материальных объектов. Однако распространение, без всяких оговорок, предположения о возможности локализации физических объектов в трехмерном пространстве и во времени на элементарные частицы материи, т е. на чрезвычайно легкие объекты, как это было сделано на заре развития атомной физики, – слишком смелая экстраполяция. В действительности, для этих элементарных объектов классические понятия пространства и времени не будут более справедливы, и мы сможем использовать их теперь лишь с ограничениями, которые и составляют наиболее своеобразные стороны квантовой теории. Ниже мы обсудим этот вопрос более подробно. Пока же нам достаточно указания, на какую гипотезу, заведомо справедливую только для объектов нашего масштаба, опирается метод изучения и описания движения материальных тел, вытекающий из классической механики.

Читайте также

2. Законы Ньютона и динамика материальной точки

2. Законы Ньютона и динамика материальной точки Приняв за основу возможность локализации физических объектов в пространстве и во времени, классическая механика начинает изучение законов движения с наиболее простого случая: с изучения законов движения материальной

3. Динамика системы материальных точек

3. Динамика системы материальных точек В динамике материальной точки поле сил предполагается заданным в каждой точке для каждого момента времени. Но в классической механике силовое поле, действующее на какую-либо материальную точку, само создается другими материальными

3. Релятивистская динамика

3. Релятивистская динамика Классические уравнения ньютоновой механики инвариантны относительно преобразования Галилея. И если рассматривать это преобразование как соотношение, отражающее истинную связь между координатами, измеряемыми двумя наблюдателями,

КИНЕМАТИКА

КИНЕМАТИКА Выше мы уже упоминали, что астрономическое направление кинематических исследований в средневековой Европе почти не развивалось.В эпоху Возрождения потребности естествознания и запросы техники, и особенно потребности астрономии, определяют особый интерес к

ДИНАМИКА

ДИНАМИКА Итак, в эпоху Возрождения были разрешены многие проблемы элементарной статики, значительные результаты получены в области кинематики. Динамика же фактически начинала делать только первые шаги.Базой для этих первых шагов было, как и ранее, критическое

3.5. Динамика тел в Главном поясе. Механизм переноса вещества в область планет земной группы

3.5. Динамика тел в Главном поясе. Механизм переноса вещества в область планет земной группы Главный пояс астероидов — образование, имеющее сложную динамическую структуру. Эта структура в основном определяется силами, действующими на малые тела в этой области со стороны

Источник

Кинематика и динамика

Механика – раздел физики, в котором изучается механическое движение, причины, вызывающие это движение, и происходящие при этом взаимодействия между телами.

Механическое движение – изменение с течением времени взаимного положения тел или их частей (частиц) в пространстве.

Кинематика – раздел механики, в котором изучают геометрические свойства движения и взаимодействия тел в не связи с причинами их порождающими.

Физические модели (научные абстракции) классической механики:

1) материальная точка – протяженное тело, размерами которого в условиях данной задачи можно пренебречь, обладающее массой. Понятие применимо при поступательном движении или когда в изучаемом движении можно пренебречь вращением тела вокруг его центра масс;

2) абсолютно твердое тело – тело, расстояние между двумя любыми точками которого в процессе движения остается неизменным. Применимо, когда можно пренебречь деформацией тела;

3) сплошная изменяемая среда – понятие применимо при изучении движения изменяемой среды (деформируемого твердого тела, жидкости, газа), когда можно пренебречь молекулярной структурой среды.

Система единиц измерения физических величин – совокупность основных и производных эталонов. В настоящее время предпочтительной во всех областях науки и техники является система СИ.

В системе СИ единицами измерения являются:1) основные – единица измерения длины (L) – 1 м; единица измерения массы (M) – 1 кг; единица измерения времени (T) – 1 с; единица измерения температуры (Т) – 1 К; единица измерения силы тока (I) – 1 А; единица измерения силы света (I) – 1 св.; 2) дополнительные – единица измерения плоского угла – 1 рад; единица измерения телесного угла – 1 стерад.

Тело отсчета – произвольно выбранное, условно неподвижное тело, по отношению к которому рассматривается движение данного тела.

Система отсчета – произвольная система координат, связанная с телом отсчета, например: а) прямоугольная, трехмерная система координат, в точке пересечения осей которой помещают тело отсчета; б) полярная система координат, положение материальной точки (тела) в которой задается радиус – вектором r и углами j, q.

Траектория движения – совокупность последовательных положений материальной точки (тела) в процессе ее движения.

Поступательное движение – движение, при котором тело перемещается параллельно самому себе. При этом все точки тела описывают одинаковые траектории, смещенные относительно друг друга.

Положение материальной точки (тела) в прямоугольной системе отсчета в данный момент времени может быть определено: с помощью координат x, y, z – M(x,y,z); с помощью радиус – вектораr и естественным (траекторным) способом (рис. П1. 1).

Уравнения движения материальной точки (тела) в кинематике:

где x, y, z – координаты;

r_x, r_y, r_z – проекции радиуса вектора rна соответствующие оси координат.

Основные понятия и определения кинематики материальной точки и твердого тела, движущегося поступательно:

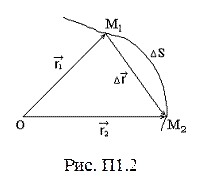
1) перемещение (рис. П1.2) – вектор Dr, проведенный из начального положения материальной точки (тела) в положение этой точки в данный момент времени (приращение радиус-вектора за рассматриваемый промежуток времени):

Dr= r₁ – r₂.

2) элементарное перемещениеdr –бесконечно малое перемещение, которое с достаточной степенью точности совпадает с соответствующим участком траектории движения. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения численно равен пройденному пути:

½Dr½= DS;

3) путь – расстояние, пройденное телом при его движении по траектории. В частных случаях перемещение и путь могут совпадать;

4) мгновенная линейная скорость – векторная физическая величина, характеризующая состояние движения, показывающая, как изменяется перемещение в единицу времени, равная первой производной от перемещения по времени:

;

5) средняя скорость неравномерного движения – скалярная физическая величина, численно равная отношению всего пути, пройденного телом (материальной точкой), к тому промежутку времени, в течение которого совершалось движение:

;

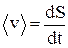
6) линейное ускорение – векторная физическая величина, характеризующая изменение скорости в единицу времени, равная первой производной от скорости или второй производной от перемещения по времени:

;

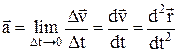
7) тангенциальное ускорение а_t – составляющая ускорения, направленная вдоль касательной к траектории движения. Изменяет линейную скорость только по величине:

;

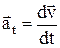
8) нормальное ускорение a_n – составляющая линейного ускорения, направленная по нормали n к вектору линейной скорости, т.е. к касательной в данной точке:

,

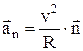
где R – радиус кривизны траектории движения;

n – единичный вектор нормали к траектории движения;

9) полное ускорение a:

.

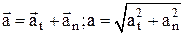
10) среднее ускорение при неравномерном движении

.

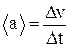
Принцип относительности Галилея (в классической механике) – никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета. Предполагается, что время не зависит от относительного движения систем отсчета.

Преобразования Галилея определяют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движется со скоростью v_o относительно другой (при условии, если направление скорости v₀ совпадает с направлением r_o):

где rи r ‘ – радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной системе отсчета в данный момент времени;

r_o – радиус вектор, определяющий положение начала координат системы К ‘ (подвижной) в системе К (неподвижной).

В проекциях на оси координат в произвольный момент времени t положение выбранной точки в системе К можно определить так:

Ковариантные или инвариантные уравнения – уравнения, обе части которых при переходе от одной системы координат к другой преобразуются одинаково и сохраняют свой вид во всех инерциальных системах отсчета.

Закон сложения скоростей в классической механике:

v= v ‘ + v₀.

Относительное расстояние между выбранными точками пространства в системах отсчета определяется соотношением – они абсолютны, т.е. инвариантны:

1) в подвижной:

;

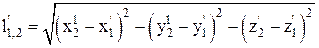
2) в неподвижной:

.

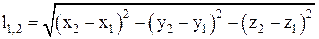
Инварианты преобразований – инвариантные величины (расстояния между телами (точками), промежутки времени между событиями, относительные скорости тел, ускорения).

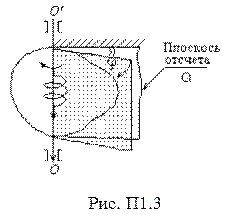
Вращательное движение твердого тела вокруг неподвижной оси –движение, при котором какие-либо две его точки остаются неподвижнымив процессе движения. Прямая, проходящая через эти точки, – ось вращения; все остальные точки твердого тела описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис. П1.3).

Основные кинематические характеристики вращательного движения (рис. П1.4):

1) угол поворотаDj – угол, отсчитанный между двумя последовательными положениями радиуса R;

2) угловая скорость w – векторная физическая величина, показывающая, как изменяется угол поворота Dj в единицу времени, численно равная первой производной от угла поворота по времени. Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта:

.

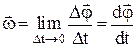
3) угловое ускорение e – векторная физическая величина, характеризующая изменение угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно – в случае замедленного:

Период вращения (T) – время, в течение которого тело совершает один полный оборот.

Частота вращения (n) – число оборотов, совершаемых в единицу времени.

Круговая (циклическая) частота ω – число оборотов, совершаемых за время, равное 2π.

Связь между периодом, частотой и круговой частотой:

ω = 2π n = 2π / T; n = 1 / T.

Связь между линейными и угловыми скоростями и ускорениями

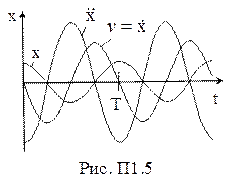
Колебательные движения (колебания) – движения или процессы, обладающие повторяемостью во времени.

Гармонические колебания (простейший вид колебаний) – движения, при которых смещение материальной точки (тела) от положения равновесия изменяется по закону синуса или косинуса (рис. П1.5):

где x – смещение это удаление материальной точки от положения равновесия в данный момент времени t;

x₀ – амплитуда колебаний это максимальное удаление материальной точки от положения равновесия;

(wt + j₀) – фаза колебаний. Периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс. Определяет положение материальной точки в данный момент времени t;

j₀ – начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t = 0;

w = 2p / T = 2p n – круговая (циклическая) частота колебаний;

T – период колебаний;

n – частота колебаний.

Скорость при гармоническом колебательном движении(колебательная скорость) – физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:

.

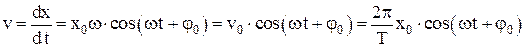
Ускорение при гармоническом колебании – физическая величина, которая показывает, как изменяется скорость в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:

.

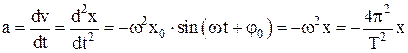
Знак «минус» означает, что ускорение направлено в сторону, противоположную смещению.

Сложение гармонических колебаний одного направления (рис. П1.6) с одинаковыми амплитудами и частотами (x₀₁ = x₀₂; w₁ = w₂ = = w), но разными начальными фазами (j₀₂ ¹ j₀₁) проводят аналитически. Уравнение результирующего колебания имеет вид

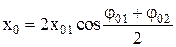
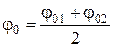
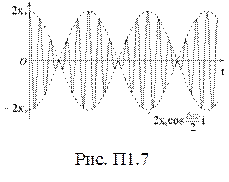
где – амплитуда результирующего колебания;

– фаза результирующего колебания.

Биениявозникают при сложение колебаний одного направления (рис. П1.7), с одинаковыми амплитудами (x₀₂ = x₀₁), начальными фазами j₀₁ = j₀₂ = 0 и круговыми частотами, мало отличающимися друг от друга (w₁ » w₂). Уравнения таких колебаний имеют вид

Уравнение результирующего колебания:

,

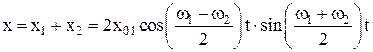
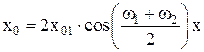
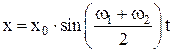
где – амплитуда результирующего колебания, которая зависит от Dw = w₁ – w₂ – разности частот складываемых колебаний;

– смещение результирующего колебания, изменяющееся по гармоническому закону.

Частота и период результирующего колебания:

Частота и период изменения амплитуды в этом случае:

Сложение взаимно перпендикулярных колебаний приводит к тому, что траектория движения представляет собой замкнутые фигуры, называемые фигурами Лиссажу (рис. П1.8):

1) сложение колебаний с одинаковыми частотами (w₁ =w₂ =w), различными амплитудами (x₀ ¹ y₀) с начальными фазами j₁ = j₂ = 0 – результирующее колебание – гармоническое. Траектория движения – прямая линия, уравнение которой имеет вид

2) сложение колебаний, начальные фазы j₁ и j₂ которых отличаются на p/2 (j₁ – j₂ = p/2) – результирующее колебание – гармоническое. Траектория движения – эллипс (при равных амплитудах x₀ = y₀ – траектория результирующего движения – окружность) с полуосями, равными x₀ и y₀, уравнение которого

3) сложение колебаний, периоды которых относятся как целые числа – через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка возвращается в начальное положение – получаются фигуры Лиссажу более сложной формы.

Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия.

Основная задача динамики – для данного тела по известной силе найти его ускорение и, наоборот, по известному ускорению найти результирующую силу, действующую на тело.

Массаm – физическая величина, характеризующая количество вещества, инертность, гравитационные свойства и энергию материального тела. Массу тела, определяющую его инертные свойства, называют инертной массой.

Центр масс (или центр инерции) системы – воображаемая точка С, положение которой характеризует распределение массы этой системы и определяется радиус-вектором:

,

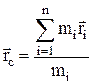
где m_i и r_i – соответственно масса и радиус-вектор i-й материальной точки;

Источник