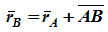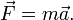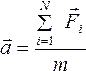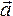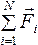Что изучает динамика поступательного движения

17.04.202221.04.2022 admin 0 Comments

Поступательное движение в школьной программе изучает предмет физика. Для понимания, что оно собой представляет, каким законам подчиняется, изучим основную терминологию и рассмотрим понятие на конкретных примерах, которые встречаются в повседневной жизни.

Что такое поступательное движение

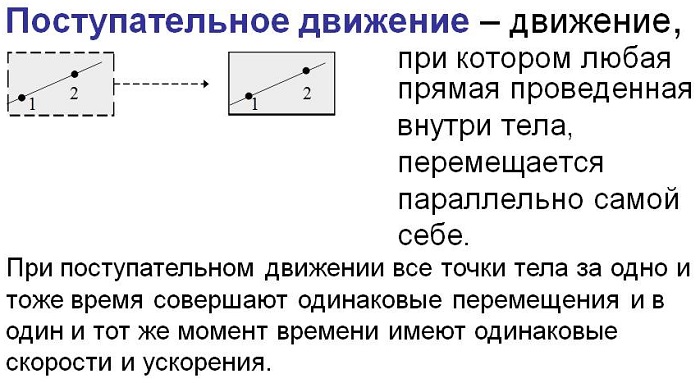
Перемещение твердого тела (всех взаимосвязанных его точек) с помощью механического воздействия по заданной траектории и в определенном направлении, в результате которого отрезок из двух любых точек данного тела будет всегда параллелен своему расположению, предшествующему нынешнему, в каждый отрезок времени, называется поступательным движением.

В процессе перемещения характеристика объекта не меняется: по составу, форме и величинам сторон. Причем в любой отрезок времени точки объекта обладают одним и тем же направлением модулей векторов скорости и ускорения, а их величины равны.

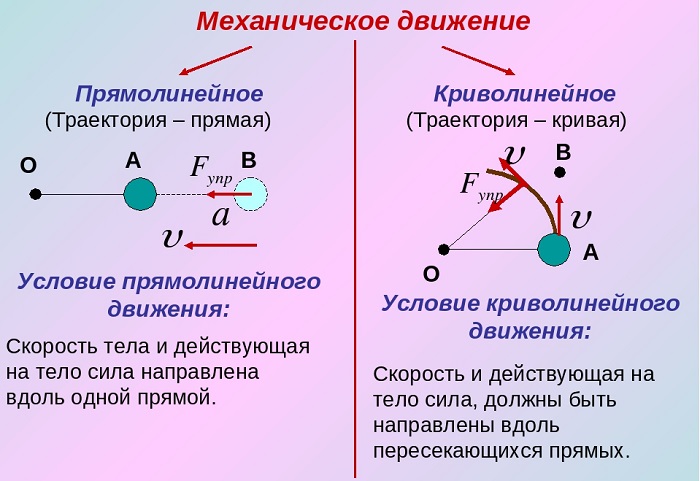
Выделяют прямолинейное поступательное движение и криволинейное.

В качестве примеров поступательного движения в можно привести функционирование по определенной траектории различного оборудования и механизмов.

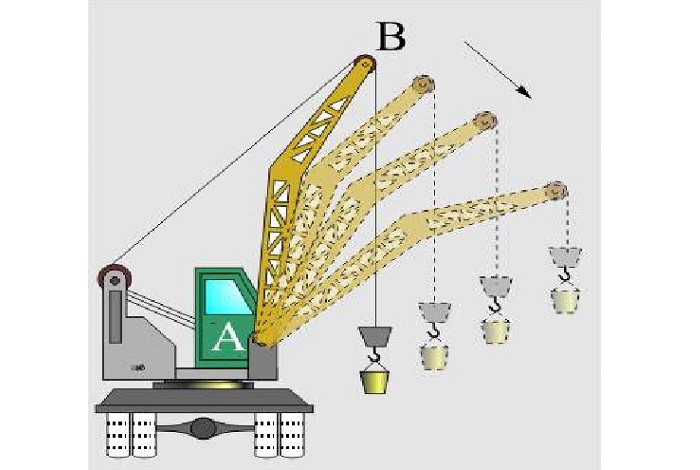
перемещение стрелы с грузом строительного подъемного крана относительно его кабины, в которой сидит рабочий;

подъем и спуск лифта в шахте;

педали у велосипеда. При этом каждая его точка, напротив, совершает вращательные движения;

совершение кабиной оборотов на колесе обозрения в парках аттракционов.

Теорема о поступательном движении

Материальные точки объекта (тела), осуществляющего поступательные движения, перемещаются по одному и тому же пути, а скорости и ускорения в каждый промежуток времени совпадают по модулю вектора и направлению.

Доказательство теоремы

Докажем данную теорему. Для этого необходимо провести прямую линию через две любые точки твердого тела, осуществляющего поступательное движение – пусть это будут точки А и В.

Полученный отрезок АВ совершает перемещение по заданному пути: А описывает траекторию АА₁А₂А₃А_n, а В соответственно – В₁В₂В₃В_n.

Отсюда следует, что:

Принимая во внимание, что размеры данного отрезка АВ неизменны (const) при перемещении, а сам он имеет свойство двигаться в пространстве параллельно своему предыдущему местоположению, значит направления точки А и точки В совпадают.

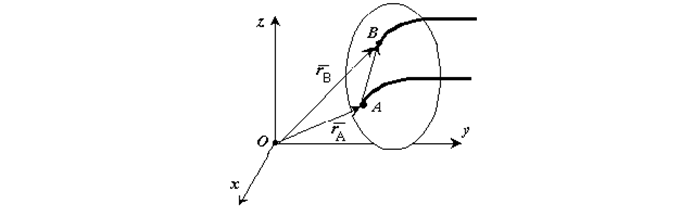
Соотношение радиусов-векторов точек А и В в системе координат относительно ее начала – О (Рис 1),

можно выразить формулой:

где линии пути точки А соответствует функция r_A(t), точки B – r_B(t).

Теорема доказывает, что для определения поступательного движения твердого материального объекта достаточно знать параметры перемещения любой одной его точки. Следовательно, изучая кинематику передвижения точки тела, решается задача определения поступательного движения.

Основной закон динамики поступательного движения

Основной закон динамики поступательного движения трактует II закон Ньютона.

Формулировка закона звучит следующим образом:

Совокупность равнодействующих сил, оказывающих воздействие на материальное тело, способствует возникновению ускорения. То есть, ускорение прямо пропорционально векторному суммарному значению оказываемых на него сил, и обратно пропорционально массе объекта.

Основное уравнение закона приведено ниже:

Причем у равнопеременного движения векторное ускорение

II закон Ньютона работает исключительно в ИСО (инерциальная система отсчета), где объекты двигаются равномерно, прямолинейно или находятся в состоянии покоя.

Источник

Физика Б1.Б8.

Электронное учебное пособие по разделу курса физики Механика

Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.

Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.

Введение

Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.

Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).

Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.

В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.

Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.

Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.

Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.

Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.

Источник

Динамика поступательного движения

Динамика поступательного движения

Динамика изучает движения тел и причины, вызывающие это движение.

Чтобы решить основную задачу механики, необходимо выбрать рациональную систему отсчета и выяснить причины возникновения ускорений. Раздел механики, где решаются эти задачи называется динамикой. Механику, основанную на законах Ньютона называют классической механикой.

Масса –мера количества вещества. F=ma, F=G * m1 * m2 * / R*R

Импульс тела –количество движения. P = m v (вектор) – справедливо для матерьяльной точки. Если тело имеет конечный размер, то импульс этого тела можно найти как векторную сумму импульсов матерьяльных точек, на которое можно разбить это тело. P – импульс.

Сила –мера взаимодействия тел друг с другом. 4 вида взаимодействий:

1. Гравитационное – взаимодействие притяжения 2х тел, обладающих массой.

2. Слабые взаимодействия – ответственно за некоторые виды распада элементарных частиц, в частности за бета-распад.

3. Электро-магнитные взаимодействия – кулоновская и лоренцева силы.

4. Сильное взаимодействие – обеспечивает связь нуклонов в ядре. Закон всемирного тяготения:

F=G m1 m2 / R * R; Fk = (1 / 4ПИ * Rнулевое) * (E1 E2 / R * R);

1 закон Ньютона:Если на тело не действуют никакие силы или равнодействующая всех сил равна нулю, то тело находится в состоянии покоя или равномерного прямолинейного движения. Согласно этому закону всякое тело, не подверженное внешнему воздействию находится в покое, либо движется равномерно и прямолинейно.

Первый закон выполняется только в инерциальных системах отсчета. В инерциальных системах отсчета ускорение тела может быть вызвано только его взаимодействием с другими телами.

2 закон Ньютона:F = ma (F,a-векторы); a = F / m; ma=F1+F2+…+Fn;

a=dv/dt; F=m dv / dt = d(wv) / dt = dP / dt; [ F = dP / dt ]; В таком виде 2ой закон применяется для описания движения тела с переменной массой.

Fх= dPx / dt= m dVx / dt= m d2 X / d t*t; Fy= m d2 Y / d t*t; Fz= m d2 Z / t*t

3 закон Ньютона:2 тела действуют друг на друга с силами, направленными вдоль одной прямой. Эти силы равны по величине и противоположны по направлению. 3-ий закон позволяет перейти от динамики отдельной матерьяльной точки к динамике системы матерьяльных точек. Это следует из того, что и для сист.мат. точек взаимодействия этих матерьяльных точек сводятся к парным взаимодействиям.

Закон сохранения импульса

Замкнутой системой матерьяльных точекназывается система матерьяльных точек, рассматриваемое как единое целое. Силы, действующие между матерьяльными точками, входящими в замкнутую систему называются внутренними. Силы, с которыми на мат.точки замкнутой системы действуют внешние тела, называются внешними.

Согласно 3му закону Ньютона геометрическая сумма внутренних сил равна нулю.

(F’ – внутр., F – внеш.) Пусть система состоит из n матерьяльных точек:

[знак системы] d (m1 v1) / dt = F1’ + F1; ….; d (mn vn) / dt = Fn’ + Fn.

(d / dt) * (m1 v1 + … + mn vn) = F1 + … +Fn

Закон сохранения импульса: Если равнодействующая всех сил, приложенных к замкнутой системе матерьяльных точек равна нулю, то суммарный импульс в замкнутой системе остается постоянным.

Закон сохранения импульса является одним из фундаментальныхзаконов физики. Он справедлив не только в классической механике, но и в квантовой. Закон сохранения импульса является следствием определенного свойства симметрии пространства – его однородность. При параллельном переносе в пространство замкнутой системы как целого, ее физические свойства и законы движения не изменяются. Импульс системы матерьяльных точек может быть выражен через импульс центромасс этой системы.

m1 g (Xc – X1) = m2 g (X2 – Xc); m1 Xc – m1 X1 = m2 X2 – m2 Xc;

(m1 + m2) Xc = m1 X1 + m2 X2; Xc = (m1 X1 + m2 X2) / m;m= m1 + m2;

Xc= (сумма Mi Xi) / m ; r центромасс = (сумма m * r) / m ;

v центромасс = dr / dt = (d / dt)*([сумма m*v] / m) = (сумма m * dv / dt) / m =

(сумма m*v) / m = P / m ; P = m * v центромасс ;Видно, что сумма импульсов замкнутой системы матерьяльных точек равен импульсу центромасс этой системы – dP / dt = F1 +…+Fm ;

m * (dv центромасс / dt) = F1+…+Fm

dP / dt = F ; dP = F * dt. Произведение силы на время ее действия называется импульсом силы.

Реактивное движениею Уравнение Мещерского.

(рисунок – летящая ракета, подписи – t+dt ; m –dm ; v+dv ; над хвостом подпись – dm (u+v)). dP = (m – dm)(v dv) + (u + v)dm – mv = mv +vdm + mdv – dm dv + udm + vdm – mv = mdv + udm. dP = mdv + udm ; Разделим обе части на dt: dP / dt = mdv / dt + udm / dt ;ma = F – udm / dt ; Fp = udm / dt (реактивная сила). [m*a = F – Fp] – уравнение Мещерского.

v – конечная скорость, u – скорость истока газа, m – масса ракеты.

Закон сохранения энергии.

Работа и кинетическая энергия. Мощность.

В качестве единой количественной меры различных форм движения материи и соответствующих им взаимодействий в физике вводится скалярная величина, называемая энергией.

Движение –неотъемлемое свойство материи, поэтому любое тело, любая система тел и полей обладает энергией.

Энергия системы количественно характеризует систему в отношении возможных в ней превращений движений.

Изменение механического движения тела и следовательно его механической энергии возможно за счет действия на это тело других тел, т.е. сил. Элементарной работой, силой F, называется величина, равная

dA>0, если АЛЬФА – острый угол и dA = w 0, то процесс становится апериодическим.

Основы термодинамики

Термодинамический процесс –это переход термодинамической системы из одного состояния в другое. Термодинамический процесс называется обратимым, если после него можно возвратить систему в исходное состояние, при этом в исходное состояние должны вернуться и все тела, взаимодействующие с системой. Процесс, который не удовлетворяет этим условиям называется необратимым. Необходимым условием обратимого процесса является его равновестность, однако не всякий равновестный процесс обратим.

Работа газа при изменении объема.dA = Fdl ; при этом сила постоянна ; dA = PS dl ; Sdl = dV ; dA = p dV ; A = (интеграл V1 – V2) P dV ;(рисунок – график, на нем правая часть гиперболы, оси – V, P ; dA – отрезок на этом графике). Графики зависимости термодинамических параметров друг от друга мы имеем право рисовать только для равновесного процесса, т.к. только для равновестного процесса значения этих параметров можно приписать всей термодинамической системе. Для неравновестного процесса, например P может быть разным для различных точек термодинамической системы. Чем медленнее протекает процесс, тем он ближе к равновестному.

Эквиваленты теплоты и работы.Обмен энергией между термодинамической системой и внешними телами может осуществляться 2мя качественно различными способами: путем совершения работы и путем теплообмена. В отсутствии внешних полей работа совершается при изменении объема или формы системы. Работа A’, совершаемая внешнми телами над системой численно равна и противоположна по знаку работе, совершаемой самой системой.

Первое начало термодинамики или первый закон термодинамики.

dQ = dU + dA ; Теплота, подводимая к термодинамической системе идет на изменение внутренней энергии и на совершение работы.

Внутренняя энергия U определяется только состоянием термодинамической системы, а Q и A являются характеристиками процесса при котором система переходит из одного состояния в другое. Переход системы из одного состояния в другое может осуществляться различными путями, поэтому Q и A зависят от способа перехода системы из одного состояния в другое, в то время, как внутренняя энергия U определяется только состоянием системы и не зависит от того, каким путем система перешла в это состояние.

Теплоемкость многоатомных газов.C = Q / m delta T ; C = dQ/ dTm ;

Cm = dQ / dT МЮ – молярная теплоемкость.В газе различают теплоемкости при постоянном давлении и теплоемкость при постоянном объеме.

1)V=const ; dV=0 ; dA=PdV=0 ; dQ=dU ; Ev = dQm / dT ; Eт = dUm / dT ;

Um = i k T Na/ 2 = i R T / 2 ; где i – число степеней свободы ;

dUm = i R dT / 2 ; Ev = i R / 2 – теплоемкость при постоянном V ;

2)P = const ; dAm = dm + dA ; dA= pdV ; PV=RT ; PdV= RdT ;

γ = Cp / Cv = (i+2) / i – коэффециент Пуассона

Из полученной формулы видно, что теплоемкость газа не зависит от температуры. Эксперементально было установленно, что этот закон соблюдается в достаточно широком интервале температур только для одноатомных газов. Уже для простых молекул – молекул H2 зависимость Cv от температуры имеет вид: Cv = i R / 2 (рисунок – график, ступеньки; оси T, Cv). Такая зависимость теплоемкости от температуры обусловлена тем, что в случае простейшей молекулы нарушается принцип равновестного распределения энергии по степеням свободы. Вращательное и колебательное движение молекул квантуются, т.е. энергия вращательных и колебательных движений не может принимать любые значения, а может иметь только вполне определенные дискретные значения. При низких температурах энергии не достаточно, чтобы возбудить вращательное и колебательное движения молекул, поэтому вращательные и колебательные степени свободы “выморожены” и не участвуют в создании теплоемкости, поэтому при низких температурах молекулы H2 имеют только 3 степени свободы (поступ.) и Cv= 3R / 2. При увеличении температуры возбуждается сначало вращательное движение (i = 5, Cv = 5 R / 2), а затем при достаточно высокой температуре и колебательном движении (i =7, Cv = 7R / 2), т.е. число степеней свободы зависит от температуры.

Применение 1-го начала термодинамики к изопроцессам и адиабатическому процессу.

1)V = const изохорный => dV=0 ; d = PdV=0 ; dQ=dU ;dU = МЮ dUмол = МЮ Cv dT ;

dQ= МЮ Cv dT ; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 – T1)/ μ

2)T = const изотермический => dT= 0 ; dQ= МЮ Cv dT = 0 ; dQ = dA ;

dA = PdV ; PV = МЮ RT ; P= МЮ RT / V ; dA = МЮ RT dV / V ;

A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT ln (V2/ V1) = МЮ RT ln (P1/ P2) ; P1 V1 = P2 V2 ;

3)P = const изобарический => dQ = PdV ; A = (интеграл V1 – V2) PdV = P (V2 – V1) ; A = P (V2 – V1) ;dU = МЮ Cv dT ; PdV = МЮ RdT ; dQ = МЮ Cv dT + МЮ Rdt = МЮ (Cv + R) dT ; Q = МЮ Cp (T2 – T1) ;

Энтропия.Помимо внутренней энергии, которая является только функциональной составляющей термодинамической системы, в термодинамике используется еще ряд других функций, описывающих состояние термодинамической системы. Особое место среди них занимает энтропия.Пусть Q – теплота, полученная термодинамической системой в изотермическом процессе, а T – температура, при которой произошла эта передача теплоты. Величина Q/ T называется приведенной теплотой.Приведенное количество теплоты, сообщаемое термодинамической системе на бесконечно малом участке процесса будет равно dQ / T. В термодинамике доказывается, что в любом обратимом процессе сумма приведенных количеств теплоты, передаваемая системе на бесконечно малых участках процесса равна нулю. Математически это означает, что dQ/T – есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от того, каким путем перешла система в такое состояние. Функция, полученный дифференциал которой равен dS= dQ/ T – называется энтропией.Энтропия определяется только состоянием термодинамической системы и не зависит от способа перехода системы в это состояние. S – энтропия. Для обратимых процессов delta S = 0. Для необратимых delta S > 0 – неравенство Клаудио.Неравенство Клаудио справедливо только для замкнутой системы. Только в замкнутой системе процессы идут так, что энтропия возрастает. Если система незамкнута и может обмениваться теплотой с окружающей средой, ее энтропия может вести себя любым образом ; dQ = T dS ; При равновестном переходе системы из одного состояния в другое dQ = dU + dA ; delta S = (интеграл 1 – 2) dQ / T = (интеграл) (dU + dA) / T. Физический смысл имеет не сама энтропия, а разность энтропий при переходе системы из одного состояния в другое.

Связь энтропии с вероятностью состояния системы.Более глубокий смысл энтропии скрывается в статической физике. Энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы. Иными словами W – это число микросостояний, которые реализовывают данные макросостояния.

Больцман методами статистической физики показал, что энтропия S системы и термодинамическая вероятность связаны соотношением: S= k ln (W) ;где k – постоянная Больцмана. Термодинамическая вероятность W не имеет с математической вероятностью ничего общего. Из этого соотношения видно, что энтропия может рассматриваться как мера вероятности состояния термодинамической системы, энтропия является мерой неупорядоченной системы. Чем больше число микросостояний, реализующих данное макросостояние, тем больше ее энтропия.

Второй закон термодинамики.Количество теплоты, полученное от нагревателя, не может быть целиком преобразовано в механическую работу циклически действующей тепловой машиной. Это и есть 2ой закон: в циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от источника энергии – нагревателя.(by Кельвин Copyright 1851). Второй закон связан с необратимостью процессов в природе. Возможна другая формулировка: невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от холодного тела к горячему.Второй закон имеет вероятный характер. В отличие от закона сохранения энергии, второй закон применим лишь к системам, состоящим из очень большого числа частиц. Для таких систем необратимость процессов объясняется тем, что обратный переход должен был бы привести систему в состояние ничтожно малой вероятностью, практически не отличимой от невозможности.

Самопроизвольные процессы в изолированной системе всегда проходят в направлении перехода от маловероятного состояния в более вероятное.

Явление переноса

Теплопроводность.

Если в некоторой области газа средняя кинетическая энергия молекул больше, чем в остальных областях, то за счет хаотического движения молекул и соударений между ними происходит постоянное вырабатывани кинетической энергии молекул по всему объему газа. Энергия переносится из областей, где температура газа выше в те области, где она ниже.

æ = 1/3 c p ;c – теплоемкость, p – плотность.

Диффузия –это обусловленное тепловым движением выравнивание концентрации смеси нескольких веществ. Этот процес наблюдается в газах, жидкостях и твердых телах.

Рассмотрим двухкомпонентную смесь. Будем считать, что молекулы обеих компонент обладают близкими массами и близкими значениями эффективных диаметров. В этом случае можно считать, что и у молекул обеих компонент одинаковы. Эмпирическое уравнение диффузии имеет вид: dm_i = Д (dp_i / dx) dS dt.

Д – коэффициент диффузии.

Д = (1/3) ; dpi / dx – градиент плотности ; Т.к. и для обеих компонент смеси примерно одинаковы, то и коэффициент диффузии для них будет одинаков.

……….. При увеличении температуры газа возрастает скорость теплового движения молекул и следовательно частота соударений между ними. Следствием этого является увеличение переноса импульса от одного слоя газа к другому, поэтому при увеличении температуры газа, его вязкость возрастает.

Иная картина наблюдается в жидкостях. В жидкостях основной причиной возникновения внутреннего трения являются межмолекулярные взаимодействия (которые в газе практически отсутствуют). С увеличением температуры жидкости возрастает скорость теплового движения молекул и их кинетической энергии оказывается достаточно для разрыва межмолекулярных связей. Это приводит к ослаблению взаимодействия между молекулами и как следствие уменьшению вязкости жидкости.

Макроскопические состояния

Динамические и статистические закономерности в физике.В молекулярной физике приходится иметь дело с очень большим числом частиц (порядка числа Авогадро). Казалось бы можно записать уравнение движения для каждой частицы и затем, решив систему уравнений, описывающих все частицы, описать поведение колектива из этих частиц в целом, однако такая задача оказывается невыполнимой даже по чисто техническим причинам. В настоящее время с помощью мощных ЭВМ удается решать такую задачу для коллектива 1000 частиц. Результат такого решения показывает, что даже в этом случае поведение коллектива не зависит от поведения каждой частицы в отдельности. Поведение коллектива в целом является результатом усреднения поведения каждой частицы в отдельности, поэтому в молекулярной физике применение обычных законов динамики не позволяет описать поведение колектива из большого числа частиц, поэтому физические свойства макроскопических систем в молекулярной физике изучаются двумя взаимодополняющими друг друга методами – статистическим и термодинамическим.

Статистический метод основан на использовании теории вероятности и определенных моделях изучаемой системы. Поведение большого числа частиц, координаты и импульсы которых меняются случайным образом, проявляет статистические закономерности.

Раздел физики, в котором с помощью статистического метода изучаются физические свойства макроскопических систем называется статистической физикой.Связь между динамическими закономерностями, описывающими поведение каждой частицы в отдельности и статистические закономерности, описывает поведение системы в целом, заключается в том, что законы движения отдельных частиц после усреднения по всей системе определяют ее свойства.

Термодинамический метод основан на анализе условий и количественных соотношений превращений энергии, проходящих в системе. Термодинамический метод не рассматривает поведение каждой частицы в отдельном.

Макроскопические состояния.

Термодинамическая система –совокупность макроскопических тел, которые могут обмениваться энергией между собой и внешней средой. Термодинамическая система может находится в различных состояниях, отличающихся температурой, давлением и т.д. Величины, характеризующие состояние системы называются параметрами состояния(давление, объем и т.д).

Если термодинамическая система находится в равновесном состоянии, то параметры состояния имеют определенное значение, которое остается постоянным для всех точек термодинамической системы.

В случае неравновесногосостояния параметры состояния не имеют определенного значения для всей термодинамической системы, например, если нагреть газ с одной стороны сосуда, в котором он находится, то температура в различных частях этого сосуда будет различной.

Если термодинамическую систему, находящуюся в неравновесном состоянии изолировать от внешних воздействий (предоставить самой себе), то через некоторое время она самопроизвольно перейдет в равновесное состояние. Такой переход называется релаксацией.А время, в течении которого это происходит называется временем релаксации.Переход системы из неравновесного состояния в равновесное происходит за счет теплового движения частиц. Переход термодинамической системы из одного состояния в другое называется термодинамическим процессом.

Термодинамический процесс называется равновесным, если в этом процессе система проходит непрерывный ряд бесконечно близких равновесных состояний. Очевидно, что реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он происходит, поэтому равновесные процессы называются квазе-статическими.

Уравнение состояния идеального газа.Параметры состояния связаны друг с другом. Уравнение состояния устанавливает связь между параметрами состояния. В простейшем случае состояние термодинамической системы описывается тремя параметрами – P, V, T.

F (P, V, T) = 0 ; Идеальный газ –это модель, которая во многих случаях с достаточно хорошей точностью описывает поведение газа. Идеальный газ – это газ, молекулы которого имеют пренибрежительно малый объем и не взаимодействуют на расстоянии. Молекулы идеального газа взаимодействуют друг с другом только в момент соударения. Причем соударение считается абсолютно упругим. Эти предположения (отсутствие взаимодействия, абсолютно упругие соударения) позволяют утверждать, что внутренняя энергия идеального газа определяется суммой кинетических энергий отдельных частиц, причем эта кинетическая энергия не переходит ни в какие другие виды энергии. Опытным путем было установлено, что параметры состояния газа удовлетворяют условию PV / T = const ; зависящему от количества вещества ; PV / T = МЮ R ; (R – универсальная газовая постоянная = 8,31 дж/моль к) ; PV = МЮ RT – уравнение Менделеева-Клайперона.МЮ = m / μ ; 1 моль любого газа при нормальных условиях занимает ; R = k Na ; PV = МЮ Na kT ; МЮ Na = N ; PV = NkT ; P = N k T/ V ; N0 = N/ V – число молей в единице объема.

P = n0 k T –другая форма записи этого уравнения.