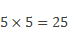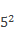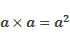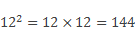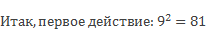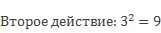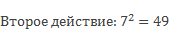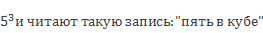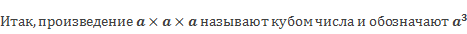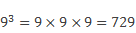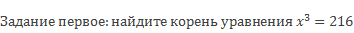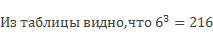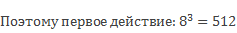Чем отличаются квадрат и куб
Разница между кубом и квадратом
Куб и квадрат в чем-то похожи. Но каждый из этих геометрических объектов имеет и собственные признаки.
Определение
Куб – тело с несколькими гранями, трехмерный геометрический объект.

Квадрат – плоская фигура, образованная равными между собой сторонами и имеющая прямые углы.

Сравнение
Уже с первого взгляда можно понять, что отличие куба от квадрата заключается в их сложности. Вторая из этих фигур является элементарной. Квадрат всегда принадлежит только одной плоскости. Его составляющие – стороны и углы. Количество тех и других – четыре. Причем в каждой группе между элементами наблюдается равенство. Квадрат рассматривается как разновидность прямоугольника, но в этом случае длина и ширина одинаковы.
Другой объект – куб – устроен сложней. Он обладает такой характеристикой, как объем. Это тело составлено из шести соединенных друг с другом квадратов, которые здесь выполняют функцию граней. Так выглядит геометрический объект в развертке:
Параметрами куба являются не только длина и ширина, но также высота. И все эти размеры у названного тела равны. Для нахождения объема нужно величину любого ребра, соединяющего соседние грани, возвести в третью степень. Если требуется найти площадь поверхности, то следует размер ребра умножить на себя же и результат увеличить в шесть раз. Между тем площадь квадрата вычисляется проще – по произведению двух сторон.
Каждый из предметов обсуждения обладает определенными свойствами. Их содержание для куба сводится к тому, какие другие многогранники можно вписать в указанный объект и как эти фигуры будут располагаться. В свойствах также упоминается о сечениях куба. В отношении квадрата говорится о равенстве и взаимной перпендикулярности его диагоналей, а также о некоторых других свойствах.
Иногда родители не знают, как на доступном уровне объяснить ребенку, в чем разница между кубом и квадратом. В таком случае можно вырезать последний из картона и продемонстрировать, какой он плоский. Затем нужно взять сделанный из бумаги или вылепленный из пластилина куб и показать его со всех сторон, чтобы хорошо просматривался объем.
Разница между кубом и квадратом
Куб и квадрат в чем-то похожи. Но каждый из этих геометрических объектов имеет и собственные признаки.
Определение
Куб – тело с несколькими гранями, трехмерный геометрический объект.

Квадрат – плоская фигура, образованная равными между собой сторонами и имеющая прямые углы.

Сравнение
Уже с первого взгляда можно понять, что отличие куба от квадрата заключается в их сложности. Вторая из этих фигур является элементарной. Квадрат всегда принадлежит только одной плоскости. Его составляющие – стороны и углы. Количество тех и других – четыре. Причем в каждой группе между элементами наблюдается равенство. Квадрат рассматривается как разновидность прямоугольника, но в этом случае длина и ширина одинаковы.
Другой объект – куб – устроен сложней. Он обладает такой характеристикой, как объем. Это тело составлено из шести соединенных друг с другом квадратов, которые здесь выполняют функцию граней. Так выглядит геометрический объект в развертке:
Параметрами куба являются не только длина и ширина, но также высота. И все эти размеры у названного тела равны. Для нахождения объема нужно величину любого ребра, соединяющего соседние грани, возвести в третью степень. Если требуется найти площадь поверхности, то следует размер ребра умножить на себя же и результат увеличить в шесть раз. Между тем площадь квадрата вычисляется проще – по произведению двух сторон.
Каждый из предметов обсуждения обладает определенными свойствами. Их содержание для куба сводится к тому, какие другие многогранники можно вписать в указанный объект и как эти фигуры будут располагаться. В свойствах также упоминается о сечениях куба. В отношении квадрата говорится о равенстве и взаимной перпендикулярности его диагоналей, а также о некоторых других свойствах.
Иногда родители не знают, как на доступном уровне объяснить ребенку, в чем разница между кубом и квадратом. В таком случае можно вырезать последний из картона и продемонстрировать, какой он плоский. Затем нужно взять сделанный из бумаги или вылепленный из пластилина куб и показать его со всех сторон, чтобы хорошо просматривался объем.
Куб и квадрат – разница и отличие между квадратом и кубом
Отличие куба от квадрата, разница между ними
Куб и квадрат часто путают, думая, что это тождественные геометрические фигуры. В действительности они отличаются друг от друга, ведь у каждого из этих объектов имеются только им присущие признаки. Какие, нетрудно понять, зная определение куба и квадрата.
Что такое квадрат и что такое куб
Фото: Квадрат
Квадрат – фигура, лежащая на плоскости, и она двухмерная. Её можно отобразить в виде прямоугольника с идентичными по длине сторонами. Квадрат можно вырезать из бумаги.
Фото: Куб
Куб же является трехмерным объектом, имеющим объём и 12 одинаковых граней. Таким образом, это правильный многогранник. Если разложить его на плоскости, то он будет состоять из 6 квадратов. Для наглядности куб можно склеить из плотной бумаги, а лучше слепить из гипса, пластилина.
Фото: разложенный куб на плоскости
В чем разница между кубом и квадратом: сравнение двух фигур
По сравнению с квадратом, куб – более сложная геометрия. Квадрат является фигурой простой, в нём только 4 стороны и 4 угла, между которыми абсолютное равенство. Квадрат можно назвать подвидом прямоугольника, только у которого ширина и длина сторон одинаковы. При этом квадрат всегда плоский. Чтобы посчитать площадь квадрата, достаточно умножить одну его сторону на другую.
Конфигурация куба сложнее, поскольку в нём уже присутствует третья мера – объём. Эта характеристика отражает пространство, которое занимает объект, в нашем случае куб. У куба также есть и третье измерение (параметр) – высота. Между собой ширина, длина и высота у куба равны.
Нахождение объема и площади
Если необходимо посчитать объем фигуры, то для расчета берут длину любого ребра между гранями и возводят её в третью степень. Для нахождения площади трехмерной фигуры куба надо узнать сумму площади всех его сторон. Поскольку они идентичны, то просто площадь одной стороны умножаем на 6. А чтобы найти площадь одной из сторон, умножаем длину ребра на себя же. Допустим, длина ребра 4 см, чтобы найти площадь одной стороны куба, 4 умножаем на 4 – получаем 16. И эту цифру уже увеличиваем в 6 раз. Значит, объём куба будет равен 96 см²
Сложные свойства куба
По сравнению с квадратом куб обладает более сложными, дополнительными характеристиками. Например, геометрический объект имеет четыре сечения, которые представляют собой правильные шестиугольники. Все сечения куба проходят через его центр и располагаются перпендикулярно относительно четырех главных его диагоналей.
Поскольку куб имеет объём, то в него можно вписать различные многогранники – такие как тетраэдр (простейший многогранник с гранями в виде 4-х треугольников), октаэдр (у этого многогранника уже 8 граней), икосаэдр (20 граней многогранника).
Чтобы ещё легче было понять разницу между кубом и квадратом, имеет смысл оценить свойства каждой фигуры наглядно. К примеру, взять обычный детский кубик с наклеенными картинками на его стороны. Так вот, сам кубик – это фигура куб, а каждая наклеенная на его сторону картинка – квадрат.
Презентация к уроку
Цель: познакомить детей с геометрическими фигурами (шар и куб). Создать условия для закрепления умения различать и называть шар (шарик) и куб (кубик).
Предварительная работа:
С детьми: Знакомство с кругом и квадратом. Сравнение геометрических фигур (круг и квадрат). Упражнение в устном счете до пяти. Закрепление приёмов лепки. Подготовка для занятия слайдовой презентации.
С родителями: Беседа с родителями о том, чтобы они дома чаще задавали детям вопросы «Какие предметы похожи на круг?», «Какие предметы похожи на квадрат?»
Перечень дидактического материала: Слайды с заданиями: «Чем отличаются круг и квадрат?», «Чем отличаются шар и куб?», «Сколько красных шаров?», «Сколько зеленых кубиков?», «Сколько кубиков всего?», слайд с динамической паузой, слайды с приемами лепки.
Оборудование: экран для воспроизведения слайдов, проектор.
Материалы: клеёнки для лепки пластилином и пластилин одного цвета на каждого ребенка.
Слайд 1.
Воспитатель: Здравствуйте дети. Вы любите сюрпризы? У меня для вас сюрприз. Смотрите, кто пришёл к нам в гости.
Слайд 2.
Воспитатель голосом медвежонка: Здравствуйте дети! Меня зовут медвежонок Мишка. Отгадайте, что у меня в коробке.
Слайд 3.
Дети: Это кубики и шары.
Слайд 4.
Воспитатель: Давайте внимательно посмотрим на шары и кубики.
Слайд 5.
Воспитатель: На какую, уже известную вам фигуру похож шар?
Дети: На круг.
Воспитатель: Правильно на круг.
Слайд 6.
Воспитатель: На какую, уже известную вам фигуру похож куб?
Дети: На квадрат.
Воспитатель: Правильно на квадрат.
Слайд 7.
Воспитатель: Посмотрите внимательно и вспомните, чем отличаются круг и квадрат.
Слайд 8.
Воспитатель: Что есть у квадрата, и нет у круга?
Дети: У квадрата есть углы. У круга нет углов.
Воспитатель: Правильно. Круг и квадрат отличаются углами.
Слайд 9.
Воспитатель: Подумайте и скажите, чем отличаются шар и куб.
Слайд 10.
Дети: Шар от куба отличаются углами.
Воспитатель: У шара нет углов и поэтому его можно катать.
Слайд 11.
Воспитатель: У куба есть углы, это придает ему устойчивость и поэтому из кубиков можно строить.
Слайд 12.
Воспитатель голосом медвежонка: А вы умеете считать? Может посчитаем?
Дети: Да!
Воспитатель: Будьте внимательны!
Слайд 13.
Воспитатель: Сколько красных шаров? Считаем вместе. Я показываю, вы называете.
Дети: Один, два.
Воспитатель: Молодцы!
Слайд 14.
Воспитатель: Сколько зеленых кубиков? Считаем вместе.
Дети: Один, два, три, четыре.
Воспитатель: Молодцы!
Слайд 15.
Воспитатель: Сколько кубиков всего? Считаем вместе.
Дети: Один, два, три, четыре, пять.
Воспитатель: Вы хорошо считаете! А теперь поиграем.
Слайд 16.
Физкультминутка.
Воспитатель:
Мы сидели тихо-тихо,
А теперь все дружно встанем
(дети встают возле своих стульчиков)
Ножками потопаем,
(дети топают)
Ручками похлопаем.
(дети хлопают)
Кубик с пола мы возьмем
И положим снова.
(дети берут с пола по кубику и кладут их с другой стороны)
Мячик в руки мы возьмем –
Передадим другому.
(дети передают мячик по кругу)
Теперь пальчики сожмем
(дети сжимают и разжимают пальцы)
А потом лепить начнем.
Слайд 17.
Воспитатель: Прошу садиться за рабочие места, чтобы приступить к лепке. Мы будем лепить кубик и шарик.
(дети садятся за подготовленные столы с клеёнками и кусочками пластилина)
Воспитатель: Сначала нужно разделить пластилин на две части.
Слайд 18.
Воспитатель: Возьмите один кусочек пластилина и придайте ему круглую форму, раскатывая кругообразными движениями между ладонями.
Это вы уже умеете и справились хорошо. Проверьте, катается ли ваш шар.
Слайд 19.
Воспитатель: А теперь задача посложнее – нужно сделать кубик. Будьте внимательными: кусок пластилина раскатываем продольными движениями ладоней и сплющиваем пальцами для получения нужной формы.
Ну что справились? Проверьте, прочно ли стоит ваш кубик.
Слайд 20.
Воспитатель: Посмотрите, как Мишка радуется вашим шарам и кубикам!
– Я тоже очень рада вашей работе!
– Но напомните мне – чем отличается шар от куба?
Дети: Шар круглый и катается, а кубик с углами и стоит прочно.
Воспитатель: Правильно. Вам понравилось занятие?
Дети: Да!
Воспитатель: И мне понравилось. Вы просто молодцы. До свидания!
Чем отличаются квадрат и куб
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы узнаете, что такое квадрат числа и куб числа, а также познакомитесь с таблицами квадратов и кубов первых десяти натуральных чисел.
Давайте рассмотрим произведение
Оказывается, это произведение можно записать иначе: 5 в степени 2, или как говорят – 5 в квадрате.
Запись эта выглядит следующим образом: пишется число 5, а число 2 записывается чуть в меньшем размере и в правом верхнем углу, вот так:
В буквенном выражении произведение 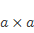
Итак, а умножить на а равно а в квадрате.
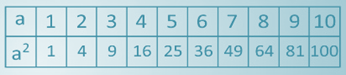
Перед вами таблица квадратов первых 10 натуральных чисел.
Из нее мы видим, что один в квадрате будет один. Два в квадрате – 4. Три в квадрате – 9. Четыре в квадрате – 16. Пять в квадрате – 25, шесть в квадрате – 36, семь в квадрате – 49, восемь в квадрате – 64, девять в квадрате – 81, десять в квадрате – 100.
Этой таблицей очень удобно пользоваться при решении следующих заданий:
Для нахождения значения данного выражения необходимо воспользоваться следующим правилом:
Если в числовое выражение входят квадраты чисел, то их значение вычисляют до выполнения остальных действий.
Третье действие: 81 – 9 = 72.
Ответ: Значение выражения равно 72.
Найдите значение выражения: (4 + 3)2 – 8.
Здесь первое действие в скобках 4 + 3 = 7.
Третье действие: 49 – 8 = 41.
Ответ: Значение выражения равно 41.
Переходим к следующему понятию – куб числа.
Произведение 5 * 5 * 5 называют кубом числа 5 и обозначают следующим образом:
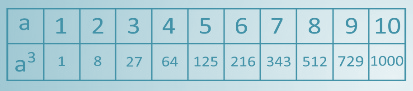
Как и в случае с квадратами, существует таблица кубов первых десяти натуральных чисел. Она имеет следующий вид:
один в кубе равно 1, два в кубе равно 8, три в кубе равно 27, четыре в кубе равно 64, пять в кубе равно 125, шесть в кубе равно 216, семь в кубе равно 343, восемь в кубе равно 512, девять в кубе равно 729, десять в кубе равно 1000.
Давайте выполним несколько заданий с использованием данной таблицы.
Значит корень уравнения х = 6.
Задание второе: найдите значение выражения: 83 + 11.
Здесь, как и в случае с квадратами чисел, воспользуемся правилом:
Если в числовое выражение входят кубы чисел, то их значение вычисляют до выполнения остальных действий.
Второе действие 512 + 11 = 523.
Таким образом, в этом уроке Вы узнали, что такое квадрат числа и куб числа, а также познакомились с таблицами квадратов и кубов первых десяти натуральных чисел.
Кроме того, получили правило для нахождения значения числового выражения: если в числовое выражение входят квадраты и кубы чисел, то их значение вычисляют до выполнения остальных действий.