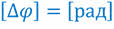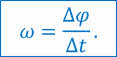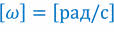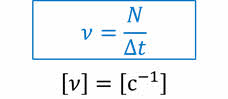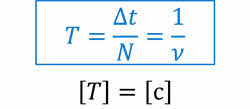Чем отличаются прямолинейные и криволинейные движения

Чем отличаются прямолинейные и криволинейные движения

Какое движение называется криволинейным?

При прямолинейном движении тела траектория представляет собой прямую линию.

Криволинейным движением называется движение, траектория которого представляет собой кривую линию.
При криволинейном движении непрерывно изменяется направление движения, т. е. направление вектора скорости, а значит, и направление вектора ускорения.

Траектория криволинейного движения может быть представлена в виде совокупности дуг окружностей разных радиусов.

1. Как на опыте с шариком на резинке показать особенности прямолинейного движения?
Под действием какой силы шарик приобретает скорость и движется от В к А?
В результате чего эта сила возникла?
Как направлены ускорение, скорость шарика и действующая на него сила?
По какой траектории движется шарик?

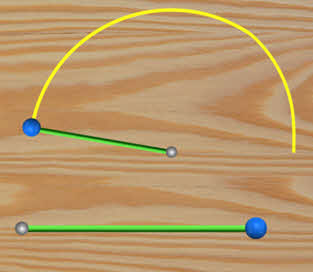
Шарик привязан к одному из концов резинового шнура.
Второй конец шнура прикреплён к столу в точке О.
Шарик находится в точке А.
Если шарик переместить в точку В, то шнур растянется.
При деформации шнура (растяжении) в нём возникнет сила упругости F, Которая действует на шарик и стремится вернуть его в первоначальное положение.

Если теперь отпустить шарик, то под действием силы упругости F он будет ускоренно двигаться к точке А.
Скорость шарика в любой точке траектории сонаправлена с силой упругости и ускорением, возникшим в результате действия этой силы.
Меняется только модуль вектора скорости шарика.
Направление вектора скорости остаётся неизменным.
Шарик движется по прямолинейной траектории.

Если скорость тела и действующая на него сила направлены вдоль одной прямой,то тело движется прямолинейно.

2. Как на опыте с шариком на резинке показать особенности криволинейного движения?
Почему в шнуре возникла сила упругости и как она направлена по отношению к самому шнуру?
Что можно сказать о направлении скорости шарика и действующей на него силы упругости шнура?
Как движется шарик — прямолинейно или криволинейно?

Шарик на резиновом шнуре ОА находится в точке А.
Толкнём шарик к точке В, т. е. придадим ему начальную скорость, направленную перпендикулярно отрезку ОА.
Если бы на шарик не действовали никакие силы, то он по инерции сохранял бы величину и направление полученной скорости.
Но, двигаясь к точке В, шарик удаляется от точки О и чуть-чуть растягивает шнур.

В шнуре возникает сила упругости F, стремящаяся сократить шнур до первоначальной длины и одновременно приблизить шарик к точке О.
В результате действия силы F направление скорости шарика в каждый момент его движения меняется, и он движется по криволинейной траектории АС.
В любой точке траектории скорость шарика v и сила F направлены вдоль пересекающихся прямых.
Шарик движется по криволинейной траектории.

3. При каком условии тело под действием силы движется прямолинейно, а при каком — криволинейно?

Действие на тело силы может привести к разным результатам в зависимости от направления векторов скорости и силы:

Если скорость тела и действующая на тело сила направлены вдоль одной прямой, то тело движется прямолинейно,
Если скорость тела и действующая на тело сила направлены вдоль пересекающихся прямых, то тело движется криволинейно.

Для криволинейного движения верно и обратное утверждение:

Если тело движется криволинейно, то это значит, что на него действует какая-то сила, меняющая направление скорости, причём в каждой точке сила и скорость направлены вдоль пересекающихся прямых.

Источник

Прямолинейное и криволинейное движение. РД тела по окружности

Урок 17. Физика 9 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямолинейное и криволинейное движение. РД тела по окружности»

На одном из прошлых уроков мы с вами говорили о том, что всякое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока на него не подействуют силы. То есть действие силы необходимо не для того, чтобы сохранить скорость тела постоянной, а чтобы изменить её. При этом действие силы может изменить как модуль скорости, так и её направление.

На экране вы видите шарик, закреплённый на столе с помощью резинового шнура. Если мы переместим шарик на некоторое расстояние, то шнур растянется и в нём возникнут силы упругости. Отпустим шарик. Под действием сил упругости он придёт в ускоренное движение и будет двигаться к своему первоначальному положению. При этом скорость шарика в любой точке траектории совпадает с направлением действующей на него силы, и, соответственно, с направлением вектора ускорения. Следовательно, при таком движении меняется только численное значение скорости, а направление её вектора остаётся неизменным, и шарик движется прямолинейно.

Повторим эксперимент. Но теперь мы не будем перемещать шарик, а толкнём его, придав некоторую начальную скорость, направленную перпендикулярно шнуру.

Если бы на шарик не действовали никакие силы, то, согласно закону инерции, он сохранял бы модуль и направление полученной скорости. Но, двигаясь, наш шарик удаляется от точки крепления шнура и слегка растягивает сам шнур. В результате в шнуре возникает сила упругости, пытающаяся вернуть его к первоначальной длине и одновременно с этим приблизить шарик к точке крепления шнура. Таким образом, в результате действия силы направление скорости шарика в каждый момент времени изменяется и шарик движется по криволинейной траектории. При этом в любой точке траектории, скорость направлена по касательной, а сила — к точке крепления шнура.

Рассмотренные примеры показывают, что действие на тело силы может привести к разным результатам в зависимости от направления векторов скорости и силы: если скорость тела и действующая на него сила направлены вдоль одной прямой, то тело движется прямолинейно, а если они направлены вдоль пересекающихся прямых, то тело движется криволинейно.

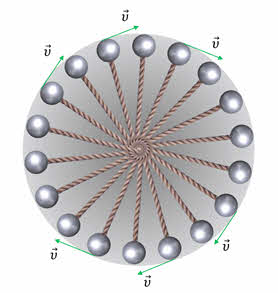
Криволинейное движение встречается гораздо чаще прямолинейного. С детства мы наблюдаем различные виды криволинейного движения, например, вращательное движение. Кто из нас не катался на карусели или не наблюдал за вращением волчка. Во вращательном движении участвуют и космические тела: планеты движутся вокруг Солнца, а спутники планет — вокруг планет.

Вообще, существует бесчисленное множество различных криволинейных траекторий. Однако любая кривая может быть представлена в виде совокупностей дуг окружностей разных радиусов. Поэтому чаще всего изучение криволинейного движения тела сводится к изучению его движения по окружности. Мы будем изучать самый простой вид такого движения — движение тела по окружности с постоянной по модулю скоростью. Таким телом, вращающимся с постоянной скоростью вокруг неподвижной оси, могут быть точильный круг, колесо автомобиля, винт самолёта и так далее.

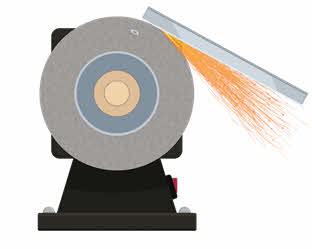
Мгновенная скорость движения тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. В этом можно убедиться, если прижать к вращающемуся точильному камню конец детали.

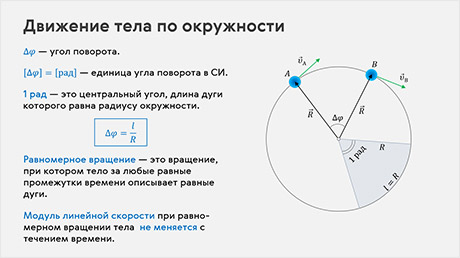
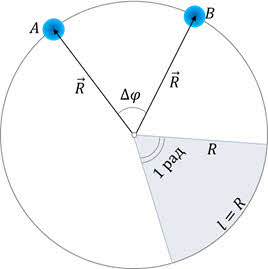
Теперь рассмотрим материальную точку, движущуюся по окружности радиусом R. Будем задавать положение этой точки с помощью радиус-вектора, проведённого из центра окружности к материальной точке.

При движении точки по окружности её радиус-вектор непрерывно поворачивается — совершает вращательное движение. Например, если за время Δt движущаяся точка переместится по окружности из точки А в точку B, то за это время её радиус-вектор повернётся на угол Δφ, который называют углом поворота.

В СИ угол поворота измеряется в радианах.

Угол в один радиан — это центральный угол, длина дуги которого равна радиусу окружности. Значение любого угла в радианах равно отношению длины дуги к радиусу окружности.

Давайте посмотрим на стробоскопическую фотографию движения тела по окружности. На ней хорошо видно, что вращающееся тело за равные промежутки времени описывает равные дуги, (или поворачивается на одинаковый угол).

Следовательно, при таком движении модуль мгновенной скорости тела не меняется с течением времени. Такое вращение называется равномерным. Но будьте внимательны. При равномерном вращение не меняется только модуль скорости, но меняется её направление от точки к точке, то есть ускорение тела не равно нулю. В случае движения тела по окружности мгновенную скорость мы будем называть линейной скоростью тела.

Быстроту вращательного движения характеризуют угловой скоростью. Её обозначают буквой ω. При равномерном вращении угловая скорость определяется, как величина, численно равная углу поворота радиус-вектора за единицу времени:

Единицей угловой скорости в СИ является радиан в секунду.

Движение, при котором тело движется по окружности с постоянной угловой скоростью, называют равномерным движением по окружности.

— А связаны ли между собой линейная и угловая скорости?

Чтобы ответить на этот вопрос, давайте подставим выражение для угла поворота в формулу для угловой скорости:

Также для характеристики вращательного движения вводятся специальные величины — частота и период обращения.

Частотой обращения называется величина, численно равная числу оборотов, совершаемых телом за единицу времени:

Периодом обращения называется промежуток времени, в течение которого тело совершает один полный оборот по окружности.

Сравнивая формулы для расчёта частоты и периода обращения, можно заметить, что они взаимно обратные.

Угловая скорость, периода и частота обращения связаны между собой формулами:

Ранее мы с вами упомянули, что при равномерном вращении тела по окружности модуль линейной скорости не меняется, но меняется её направление. То есть движение по окружности всегда происходит с ускорением. Конечно у вас может возникнуть вопрос: как определить модуль и направление этого ускорения?

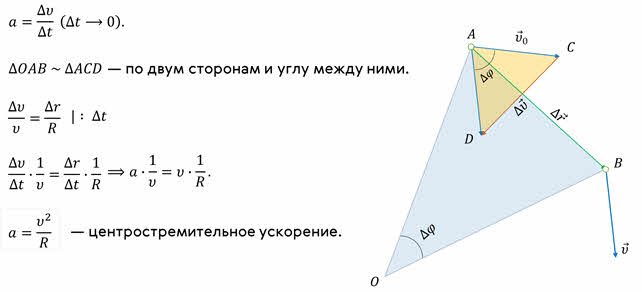
Итак, пусть материальная точка, двигаясь по окружности с постоянной по модулю скоростью, за некоторый промежуток времени перемещается из положения А в положение В. Скорость материальной точки в этих положениях направлена по касательной к окружности в этих точках.

Полученная формула определяет модуль ускорения при равномерном движении тела по окружности.

— А как направлено это ускорение?

Согласно второму закону Ньютона, ускорение всегда сонаправлено с силой, в результате действия которой оно возникает. Это справедливо и для центростремительного ускорения. Поэтому, сила, под действием которой тело движется по окружности с постоянной по модулю скоростью, в каждой точке направлена по радиусу окружности к её центру.

Источник

«Прямолинейное и криволинейное движение» Послесловие к уроку

МБОУ СОШ № 125 с УИОП, г. Снежинск, Челябинская обл

Прямолинейное и криволинейное движение

Послесловие к уроку

Сразу хочу признаться и покаяться в своем неоправданно легкомысленном на протяжении многих лет отношении к уроку в 9-м математическом классе по теме «Прямолинейное и криволинейное движение» (про базовый уровень не говорю). Ему предписывалась некая вводная роль к основному и достаточно сложному для девятиклассников материалу (надо сказать, что любой материал в школьной физике, связанный с векторами, идет трудно, начиная с седьмого класса) из § 19 [1] по описанию движения тела по окружности с постоянной по модулю скоростью. Наиболее распространенное в природе криволинейное неравномерное движение сводилось к совокупности более простых и менее распространенных движений: прямолинейному и по дугам окружностей разных радиусов. И как-то скромно, без должного почтения и ударения, после приведённых необходимых примеров, проговаривалась фраза, выделенная курсивом в учебнике [1]: «если скорость тела и действующая на него сила направлены вдоль одной прямой, то тело движется прямолинейно, а если они направлены вдоль пересекающихся прямых, то тело движется криволинейно». А зря! Такая «легкокасательная» скромность, тем более неоправданна потому, что в десятом классе [2], несмотря на систематическое и последовательное описание прямолинейного и криволинейного движения (по параболе и по окружности), никакого обобщения не предусмотрено, и вообще нигде даже не намекается на то, что ускорение, ответственное за изменение скорости по модулю, имеет в физической литературе название касательного или тангенциального ускорения. В одиннадцатом классе это естественным образом аукается при описании кинематики и динамики движения математического маятника. Авторы учебника [3] чётко и подробно рассматривают колебательный процесс, оставляя учителю объяснить учащимся, почему проекция силы тяжести и ускорения на касательную к траектории маятника имеет пресловутый индекс «τ» и никакой другой.

Подводя итог, можно сказать, что после урока по теме «Прямолинейное и криволинейное движение» в девятом классе, в учебниках старших классах не осуществляется больше попыток какого-либо системного обобщения по этому вопросу, по крайней мере, в тех учебниках, по которым работает большинство учителей.

Вернёмся к прямым линиям, вдоль которых могут быть направлены мгновенная скорость и действующая на тело сила (читай равнодействующая сила). Вывод в учебнике, выделенный курсивом не очевиден для детей и непрост. Конечно, надо поэтапно, рассматривая сначала примеры прямолинейных и более изученных движений, а затем криволинейных и менее изученных, подвести учащихся к обобщающему выводу о направлениях прямых. И, думаю, что этот вывод необходимо обосновать, опираясь на второй закон Ньютона. А сам вывод впоследствии можно использовать как критерий при описании различных видов наблюдаемых или возможных движений тела.

Итак, события на уроке развивались примерно так.

Сначала мы пытались ответить на вопрос, что такое прямолинейное движение и при каких условиях оно возможно. Выяснили, что при прямолинейном движении тело движется по прямой линий и вектор скорости не меняет своего направления. С условиями прямолинейного движения дело оказалось несколько сложнее. Во-первых, дети сразу вспомнили закон инерции, а в выводе курсивом он был как-то не предусмотрен (стало быть, вывод придется дополнять)! Во-вторых, не учли, что сила (в скобках заметим, что и ускорение, создаваемое этой силой) может быть не только сонаправлена с движением, но и противонаправлена ему. То есть скорость при прямолинейном движении не меняет своего направления, но по модулю может увеличиваться или уменьшаться. После наблюдения за движением автомобиля по столу и шарика вертикально вверх и вниз мы записали второй закон Ньютона для всех опытов, сделали приведенные ниже чертежи, специально выделив линии, вдоль которых направлены силы, ускорения и скорости, сформулировали промежуточный вывод.

Прямолинейно тело может двигаться либо по инерции, сохраняя при этом свою скорость, либо ускоренно (замедленно), если скорость тела в каждый момент времени и сила, действующая на него, направлены вдоль одной прямой в одну сторону (или вдоль одной прямой в противоположные стороны). При криволинейном движении траекторией тела является кривая линия и, следовательно, скорость должна менять свое направление.

Вспоминаем движение Луны вокруг Земли, делаем чертеж, отмечаем линии, вдоль которых направлены скорость и сила, и задаемся вопросом, а зачем вообще нужна сила тяготения? Понятно зачем, затем чтобы удержать Луну – получаю ответ. И тут наступает многозначительная пауза. А почему Луна не падает на Землю, ведь есть сила, должно быть и ускорение!? А факт таков, что скорость Луны по модулю не меняется при наличии силы и ускорения, которое должно быть (ну, почти не меняется)? И вот тут нас ждало большое открытие! Оказывается, чтобы просто (!) повернуть уже движущееся тело, нужна сила. И это еще не все, сама сила, оставаясь неизменной по модулю, должна менять свое направление! Такое открытие надо пережить и закрепить (можно, для пущей важности, еще показать движение шарика на резинке).

Мы смотрим небольшой фильм со знакомым нам зеленым человечком в роли ковбоя [4]. Приведу некоторые картинки из фильма. Вид сверху: лошадь движется по окружности, удерживаемая канатом ковбоя. Скорость лошади направлена по касательной к окружности. Если канат порвется, что и происходит в фильме, лошадь сходит с окружности и начинает двигаться прямолинейно.

Сила создает центростремительное (или нормальное) ускорение, сонаправленное с силой. Таким образом, вводим понятие центростремительного ускорения ответственного за изменение скорости по направление.

Ещё один вид криволинейного движения это движение тела по параболе, хорошо знакомый нам с детства. Конечно, при описании свободного падения тела, брошенного горизонтально, мы говорили ранее, что на тело постоянно действует только одна сила тяжести.

Мы попробовали применить выводы и формулу, полученную на уроке к описанию некоторых известных нам движений. Приведенная ниже таблица, может дополняться впоследствии и использоваться при систематизации материала.

Источник

Чем отличаются прямолинейные и криволинейные движения

Единое национальное тестирование

История Казахстана

Онлайн тесты и шпаргалки по истории Казахстана

Всемирная история

Онлайн тесты и шпаргалки по Всемирной истории.

Математика

Онлайн тесты и шпаргалки по математике.

Химия

Онлайн тесты и шпаргалки по химии.

Физика

Онлайн тесты и шпаргалки по физике.

Биология

Онлайн тесты и шпаргалки по биологии.

География

Онлайн тесты и шпаргалки по географии.

Русский язык

Онлайн тесты и шпаргалки по русскому языку.

Готовые работы

ДИПЛОМНЫЕ РАБОТЫ

КУРСОВЫЕ РАБОТЫ

МАГИСТЕРСКИЕ ДИССЕРТАЦИИ

ОТЧЕТЫ ПО ПРАКТИКЕ

После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт. Этот документ будет подтверждением практической работы студента и основой формирования оценки за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный план и описать свою практическую деятельность.
Мы поможет написать отчёт о прохождении практики с учетом специфики деятельности конкретного предприятия.

Новости сайта

Обучение по государственному образовательному заказу (магистратура)

Комплексное тестирование проводилось с 3 по 7 декабря текущего года. 10 декабря текущего года текущего года начинается прием заявлений для участия в конкурсе по присуждению государственных образовательных грантов на подготовку магистров.

Для участия в конкурсе на присуждение государственного образовательного гранта на подготовку магистров поступающий до 18:00 часов (по местному времени) 14 декабря подает заявление через виртуальную приемную комиссию любой организации высшего и послевузовского образования (далее – ОВПО). Поступающие в магистратуру в заявлении указывают одну группу образовательных программ и до 3-х (трех) ОВПО.

На обучение по государственному образовательному заказу на конкурсной основе зачисляются лица, набравшие наивысшие баллы по КТ и (или) вступительному экзамену и (или) творческих экзаменов: 1) для научно-педагогической магистратуры с казахским или русским языком обучения, в том числе по группам образовательных программ, требующих творческой подготовки, по группам образовательных программ, требующих знания арабского языка – не менее 75 баллов; 2) для профильной магистратуры с английским или с казахским или русским языком обучения – не менее 50 баллов.

Источник