Чем отличаются кинематика и динамика
Разница между кинематикой и динамикой
Содержание:
Изучение кинематики часто может быть спроектировано и решено как чисто математическая функция, что означает, что она не задает вопрос «как изменилась скорость тела?» а точнее, «насколько это изменилось?»
Изучение динамики идет рука об руку с изучением кинематики, потому что она имеет дело с силой, которая действует на движение. Попытки понять силы, которые заставляют объект или тела объекта двигаться. Изучая динамику, исследователи изучают, как физическая система может развиваться или изменяться с течением времени, и изучают причины этих изменений. Исследование динамики скорее задаст вопрос «почему скорость изменилась» и «как она может повлиять на объект в будущем».
Короче говоря, кинематика даст вам значения изменений, в то время как динамика обеспечит обоснование этого.
Сравнение кинематики и динамики:
кинематика
динамика
Исследование, описывающее движение точек, тел (объектов) и систем тел (групп объектов) без учета причин движения
Исследование сил и крутящего момента и его влияние на движение
Область исследования, используемая в
Прикладная математика, робототехника, машиностроение, робототехника, биомеханика и астрофизика
Прикладная математика, машиностроение
Относится только к свойствам движения, таким как скорость, смещение и ускорение
Относится к анализу сил, действующих на любое движущееся тело
Различие разделов Кинематика,Статика,Динамика.
(Материальная точка, Траектория, Путь, Перемещение..)
Равномерное прямолинейное движение.
Равноускоренное прямолинейное движение.
Равномерное движение по окружности.
(Равновесие тел,момент силы,плечо силы,центр масс,центр тяж.,пара сил)
| Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. |
| Безразличное: При малом отклонении тело остается в равновесии. |
| Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. |
Дина́мика — раздел механики, в котором изучаются причины возникновения механического движения.
( масса, сила, импульс, энергия.)
· Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
· Обратная задача динамики: по заданным силам определить характер движения тела.
Моменты сил,его свойства.Гармонические колебания
МОМЕНТ СИЛЫ[Hм] —величина, характеризующая вращательный эффект силы; имеет размерность произведения длины на силу. Различают момент силы относительно центра (точки) и относительно оси.
Какое-либо кинематическое состояние тел, имеющих точку или ось вращения, можно описать моментом силы, характеризующим вращательный эффект действия силы.
Плечо силы – кратчайшее расстояние от центра до линии действия силы (перпендикуляр из центра на линию действия силы).
Знак момента :
Свойства момента силы относительно центра (точки).
Модуль момента силы относительно точки равняется удвоенной площади треугольнику построенного на векторах.
Момент силы относительно точки не изменяется при перенесении силы вдоль ее линии действия, поскольку неизменным остается плечо силы.
сила равняется нулю F = 0;
плечо силы h = 0, т.е. линия действия силы проходит через центр.
+свойства
1)момент не меняется при движении точки приложения вдоль линии действия.
2)Момент = 0 если линия действия силы проходит через центр
Теорема Вариньона (о моменте равнодействующей).
Момент равнодействующей плоской системы сходящихся сил относительно какого-либо центра равняется алгебраической сумме моментов составляющих сил системы относительно того же центра.
Моментом пары называется вектор с такими признаками:
он перпендикулярен плоскости пары;
направлен в ту сторону, откуда вращение, которое осуществляет пара, видно против часовой стрелки;
его модуль равняется произведению модуля одной из сил пары на плечо пары с учетом знака
Пара сил – система двух параллельных, равных по модулю и противоположных по направлению сил, приложенных к абсолютно твердому телу.
Момент пары сил равняется произведению модуля одной из сил пары на плечо пары.
Свойство момента пары сил: момент пары равняется моменту одной из сил относительно точки приложения второй силы.
Теоремы о паре сил
* Теорема 1. Пара сил не имеет равнодействующей, т.е. пару сил нельзя заменить одной силой.
*Теорема 2. Пара сил не является системой уравновешенных сил.
* Следствие: пара сил, действующая на абсолютно твердое тело, старается вращать его.
Теорема 3. Сумма моментов сил пары относительно произвольного центра (точки) в пространстве является величиной неизменной и представляет собой вектор-момент этой пары.
Теорема 4. Сумма моментов сил, которые составляют пару, относительно произвольного центра в плоскости действия пары не зависит от центра и равняется произведению силы на плечо пары с учетом знака, т.е. самому моменту пары.
Пары сил в плоскости уравновешиваются в том случае, если алгебраическая сумма их моментов равняется нулю.
свободные (гармонические) колебания, происходящие под действием линейной восстанавливающей силы, т. е. силы стремящейся вернутьточку в положение равновесия и пропорциональной её отклонению от этого положения равновесия.(F=-kx)
Свойства пары сил.
Свойства пары сил. Первое свойство. Пару сил нельзя привести к силе. Т.е пара сил (как и сила) является самостоятельным элементом статики.
* рассмотрим сложение параллельных сил. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F1,F2) уравновешенную систему сил(Q1,Q2)
0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силамR1 и R2 (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C(рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R1 и R2 на составляющие (рис. 23, c), а затем вычитаем уравновешенную систему сил (Q1,Q2). В результате получаем, что исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F1,F2) = (F1,F2)C (рис. 23, d). По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей (рис. 23, c):
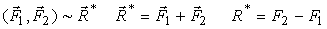 | (1) |
*Из рисунков видим, что равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB.
*При сложении двух параллельных сил, направленных в одну сторону, получается аналогичный результат, только величина равнодействующей будет равна R* = F1 + F2, а точка D будет лежать внутри отрезка AB.
*Можно распространить этот вывод и на систему из n параллельных сил, добавляя к полученной равнодействующей по одной из оставшихся сил системы. В результате мы докажем, что
*Вернемся к доказательству первого свойства пары сил. Устремим величину первой силы ко второй. При F1 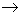
1. Кинематика и динамика
1. Кинематика и динамика
В этой небольшой главе мы отнюдь не собираемся делать какого-либо, даже краткого, обзора принципов классической механики и, тем более, критически анализировать эту область физики. Для этого недостаточно было бы и целой книги; к тому же эти вопросы уже рассмотрены многими выдающимися учеными. Мы остановимся здесь лишь на некоторых вопросах, которые, на наш взгляд, представляют интерес в связи с излагаемым материалом.
Аналитическая механика состоит из двух разделов, носящих совершенно различный характер: кинематики и динамики, частным случаем которой является статика. Необходимо вкратце остановиться на этом разделении, поскольку оно основывается на предположениях, не оправдавших себя с точки зрения квантовой теории.
В самом деле, что же такое кинематика и почему ее изучают обычно прежде, чем динамику? Кинематика изучает движения тел, происходящие в трехмерном пространстве в течение какого-то времени и совершенно независимо от физических причин этого движения. На первый взгляд кажется вполне естественным предпослать изучению динамики изучение кинематики, ибо представляется совершенно логичным сначала изучить in abstracto различные виды движения в пространстве, а уж затем задаваться вопросом, по какой причине и следуя каким законам то или иное движение возникает в тех или иных условиях. Но этот кажущийся естественным путь в действительности покоится на одной гипотезе, в чем до последнего времени не отдавали себе ясного отчета даже наиболее выдающиеся умы. Действительно, математики, очевидно, вправе заниматься изучением перемещений в пространстве трех измерений в зависимости от параметра, который может быть идентифицирован со временем. Однако речь здесь идет о том, можно ли, как это без всякого анализа предполагалось, применять результаты этого абстрактного изучения к случаю реального движения физических объектов.
Классический переход от кинематики к динамике, по существу, содержит в себе гипотезу о том, что локализация физических объектов в некоторой абстрактной области трехмерного пространства и времени возможна вне зависимости от внутренних свойств самих физических объектов, например от их массы. Совершенно достоверно известно, что если оставаться в пределах нашего масштаба, то окружающие нас материальные тела с большой степенью точности могут считаться локализованными в пространстве и во времени. Именно это свойство тел и, в частности твердых, позволяет нам наглядно представить себе трехмерное пространство, в котором они перемещаются. Движение этих тел дает нам возможность точно определить время и способ его измерения. По этому оказывается вполне естественным, что методы аналитической механики с успехом применяют для изучения движения подобного рода материальных объектов. Однако распространение, без всяких оговорок, предположения о возможности локализации физических объектов в трехмерном пространстве и во времени на элементарные частицы материи, т е. на чрезвычайно легкие объекты, как это было сделано на заре развития атомной физики, – слишком смелая экстраполяция. В действительности, для этих элементарных объектов классические понятия пространства и времени не будут более справедливы, и мы сможем использовать их теперь лишь с ограничениями, которые и составляют наиболее своеобразные стороны квантовой теории. Ниже мы обсудим этот вопрос более подробно. Пока же нам достаточно указания, на какую гипотезу, заведомо справедливую только для объектов нашего масштаба, опирается метод изучения и описания движения материальных тел, вытекающий из классической механики.
Читайте также
2. Законы Ньютона и динамика материальной точки
2. Законы Ньютона и динамика материальной точки Приняв за основу возможность локализации физических объектов в пространстве и во времени, классическая механика начинает изучение законов движения с наиболее простого случая: с изучения законов движения материальной
3. Динамика системы материальных точек
3. Динамика системы материальных точек В динамике материальной точки поле сил предполагается заданным в каждой точке для каждого момента времени. Но в классической механике силовое поле, действующее на какую-либо материальную точку, само создается другими материальными
3. Релятивистская динамика
3. Релятивистская динамика Классические уравнения ньютоновой механики инвариантны относительно преобразования Галилея. И если рассматривать это преобразование как соотношение, отражающее истинную связь между координатами, измеряемыми двумя наблюдателями,
КИНЕМАТИКА
КИНЕМАТИКА Выше мы уже упоминали, что астрономическое направление кинематических исследований в средневековой Европе почти не развивалось.В эпоху Возрождения потребности естествознания и запросы техники, и особенно потребности астрономии, определяют особый интерес к
ДИНАМИКА
ДИНАМИКА Итак, в эпоху Возрождения были разрешены многие проблемы элементарной статики, значительные результаты получены в области кинематики. Динамика же фактически начинала делать только первые шаги.Базой для этих первых шагов было, как и ранее, критическое
3.5. Динамика тел в Главном поясе. Механизм переноса вещества в область планет земной группы
3.5. Динамика тел в Главном поясе. Механизм переноса вещества в область планет земной группы Главный пояс астероидов — образование, имеющее сложную динамическую структуру. Эта структура в основном определяется силами, действующими на малые тела в этой области со стороны
Тема 1.6. Основные понятия кинематики
§1. Кинематика точки. Введение в кинематику.
Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.
Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.
Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.
Рис.1. Система отчета
Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).
Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.
Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.
Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).
Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.
Положение тела можно определить с помощью радиус-вектора или с помощью координат.
Рис.2. Радиус-вектор
Рис.3. Координаты точки М
Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.
Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.
В дальнейшем под словом «тело» будем понимать «материальная точка».
Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.
В зависимости от вида траектории различают прямолинейное и криволинейное движение.
где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).
Модуль перемещения не может быть больше пути: ≤s.
Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.
Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
Видео-урок «Механическое движение»
§2. Способы задания движения точки
Для задания движения точки можно применять один из следующих трех способов:
1) векторный, 2) координатный, 3) естественный.
1. Векторный способ задания движения точки.
Рис.4. Движение точки М
При движении точки М вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргумента t:
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.
2. Координатный способ задания движения точки.
Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости
Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.
3. Естественный способ задания движения точки.
Рис.5. Движение точки М
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси).
Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).
§3. Вектор скорости точки
Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.
Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.
Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.
Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.
Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.
Ключевое отличие: кинематика даст вам значения изменения объектов, в то время как динамика предоставит обоснование изменения объектов.
Изучение кинематики часто может быть спроектировано и решено как чисто математическая функция, что означает, что оно не задает вопрос «как изменилась скорость тела?» а точнее, «насколько это изменилось?»
Короче говоря, кинематика даст вам значения изменений, в то время как динамика обеспечит обоснование этого.
Сравнение кинематики и динамики:
кинематика
динамика
Исследование, описывающее движение точек, тел (объектов) и систем тел (групп объектов) без учета причин движения
Исследование сил и крутящего момента и его влияние на движение
Область исследования, используемая в
Прикладная математика, робототехника, машиностроение, робототехника, биомеханика и астрофизика
Прикладная математика, машиностроение
Относится только к свойствам движения, таким как скорость, смещение и ускорение
Относится к анализу сил, действующих на любое движущееся тело


