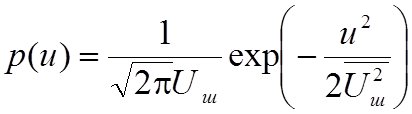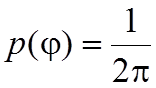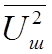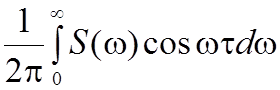Чем отличаются флуктуационные помехи

Помехи приему сигнала. Действие флуктуационных помех на приемник

Флуктуации — колебания какой-либо физической величины около своего среднего значения. Такие флуктуации э. д. с. или электрического тока неиз-бежно возникают в любых радиотехнических устройствах. Происходит это вследствие дискретной природы электрического тока (потока заряженных частиц – электронов). Поскольку эти флуктуации оказывают в радиоустрой-ствах мешающее действие и в определенных условиях могут нарушить их нормальную работу, они называются помехами. А так как эти помехи не приходят откуда-то извне, а возникают непосредственно внутри радиоуст-ройств, их называют внутренними.
Если такие внутренние помехи в достаточной степени усилить и подать на громкоговоритель, то последний будет издавать своеобразные шипящие звуки. Поэтому такие помехи принято называть шумовыми помехами или просто шумами. Такое название сохраняется даже в тех случаях, когда помеха никаких звуков не производит, как, например, при приеме телевизионных изображений.
Флуктуационная помеха — помеха, которая представляет собой случайный нормально распределенный шумовой сигнал (Гауссовский шум).
К основным видам шумовых помех относятся:
— тепловые (шум Джонсона): образуются за счет хаотического теплового движения электронов в различных активных сопротивлениях, колебательных контурах, фидерных линиях, антеннах. Тепловой шум генерируется любым резистором, находящимся в измерительной цепи. Зна-чение его состоит в том, что он устанавливает нижнюю границу напряжения шумов любого измерительного преобразователя, имеющего выходное сопротивление.
— дробовые, обязанные своим происхождением флуктуациям потока электронов во всевозможных электронных приборах (диодах, транзисторах, радиолампах). Он имеет равномерный спектр, т.е. является белым.
— фликкер – шум: к данному виду относят шумы, у которых спектраль-ная мощность на декаду частоты примерно постоянна, т.е. розовые шумы, например шум постоянного резистора, пропорциональный протекающему через него току, шум тока базы транзистора и др.
Тепловые и дробовые помехи представляют собой беспорядочную хаотическую последовательность очень малых и очень коротких импульсов, следующих друг за другом через случайные промежутки времени, вследствие чего спектр шумов является сплошным. В нем присутствуют составляющие любых частот, но из-за этого мощность каждой такой составляющей оказывается бесконечно малой. Поэтому для оценки распределения мощности шума по частотам пришлось ввести специальное понятие — спектральную плотность мощности шума. Иногда спектральную мощность шумов называют также интенсивностью шума.
Спектральная плотность мощности шума — величина постоянная от нуле-вых до самых высоких радиочастот. Поэтому флуктуационные помехи не-редко называют гладким или белым шумом (рис.6) (по аналогии со спектром белого света). Спектральные составляющие белого шума равномерно распределены по всему частотному диапазону.
Встречаются сложные источники шума, спектр которых неравномерен. Спектральная плотность мощности шума при его возникновении и постоян-на. Но при прохождении напряжения шумов по тракту в нем могут встре-титься участки, коэффициент передачи которых изменяется с частотой (различные цепи коррекции, усилители с ограниченной полосой частот, на-пример с резонансными контурами и т. п.). После таких участков спектраль-ная плотность мощности шума приобретает форму, соответствующую кривой изменения коэффициента передачи участка в зависимости от частоты.
Флуктуационную помеху полностью устранить невозможно, так как часть спектра помехи всегда накладывается на спектр сигнала. Для умень-шения влияния флуктуационной помехи на качество приема применяют частотно-избирательные цепи в радиотракте приемника.
Пространственная избирательность основана на применении антенн с диаграммой направленности заданной формы и ориентации. Особенно ши-роко этот способ стали применять в радиоприемных устройствах, работаю-щих с антеннами типа фазированных антенных решеток в диапазоне СВЧ.
Поляризационная избирательность основана на различиях поляризации полей сигнала и помех. Этот способ применяют при защите приемника от действия атмосферных помех.
Временная избирательность применяется в основном в импульсных системах. Основана на различии длительности импульсных помех и рабочих сигналов. Хорошие результаты дает дополнительная реализация метода накопления периодических сигналов на фоне белого шума.
Для защиты от импульсных помех, отличающихся по амплитуде от по-лезного сигнала, применяют: ограничитель снизу, который отделяет полез-ный сигнал от импульсных помех меньшей амплитуды, ограничитель сверху, отделяющий полезный сигнал от импульсных помех большей ам-плитуды.
Компенсационный метод защиты от помех основан на применении уст-ройства, состоящего из двух трактов: рабочего и компенсационного. Рабо-чий тракт настроен на частоту сигнала, а компенсационный расстроен на частоту Д/к. При незначительных расстройках импульсная помеха в рабочем и компенсационном трактах идентична и может быть скомпенсирована.
Флуктуационную помеху на выходе узкополосных систем можно пред-ставить:
n(t)=a(t)cos(wt-j(t))=A(t)cos t+B(t)sin t,
где A(t)-случайная медленно меняющаяся амплитуда;
B(t)-случайная фаза.

Источник

Флуктуационные помехи (шум)

Страницы работы

Содержание работы

2.2.3 Флуктуационные помехи

Флуктуационная помеха (шум) представляет собой хаотическую последовательность кратковременных импульсов, следующих друг за другом так быстро, что отдельные возмущения от каждого из них в приемнике перекрываются, образуя непрерывный случайный процесс. Типичными примерами такой помехи являются внутренние шумы приемника и космические помехи. Флуктуационный характер могут иметь и индустриальные помехи, особенно при наложении их от многих источников.

По статистическим свойствам флуктуационная помеха представляет собой стационарный случайный процесс с нормальным распределением. Одномерная плотность вероятностей мгновенных значений такой помехи описывается нормальным законом распределения (законом Гаусса).

где 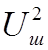– средний квадрат действующего шумового напряжения.

Фаза флуктуационной помехи имеет равномерное распределение в интервале (0-2p):

Флуктуационную помеху на выходе фильтра со средней частотой f₀ можно рассматривать как узкополосный процесс. В этом случае помеху можно представить как квазигармоническое колебание со случайными огибающей U_П(t) и фазой j(t).

Величина равная 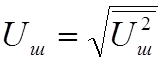называется среднеквадратичным (действующим) значением шумового напряжения.

Cреднее значение шумового направления равно нулю, а дисперсное, поэтому, численно равна

s 2 =

Скорость изменения помехи во времени характеризуется функцией корреляции, которая связана с односторонним энергетическим спектром преобразования Фурье

R(t)=

Значения случайного процесса являются некоррелированными только при неограниченной полосе.

Источник

Флуктуационные и сосредоточенные помехи

Флуктуационные помехиносят характер шума. Термин «шум» обозначает нежелательные электрические сигналы, которые всегда присутствуют в электрических системах. Наличие шума, наложенного на сигнал, «затеняет», или маскирует сигнал; это ограничивает способность приёмника принимать точные решения о значении символов, а следовательно, ограничивает скорость передачи информации. Природа шумов различна и включает как естественные, так и искусственные источники. Искусственные шумы – это шумы искрового зажигания, коммутационные импульсные помехи и шумы от других источников электромагнитного излучения. Естественные шумы исходят от атмосферы, солнца и других галактических источников.

Белый шум.

Особенностью теплового шума является то, что его спектральная плотность мощности (СПМ) одинакова для всех частот (от единиц Гц до 10 12 Гц).

Вт / Гц – постоянная величина во всём диапазоне частот.

Рис. 3. Спектральная плотность мощности белого шума

– двухсторонняя СПМ, поэтому N_о делится на 2.

Шум с постоянной СПМ во всём диапазоне частот называется белым.

Автокорреляционная функция (АКФ) белого шума даётся обратным преобразованием Фурье СПМ:

(2.6)

Таким образом, АКФ БШ – это дельта-функция, взвешенная множителем N_o / 2 и находящаяся в точке τ =0, как показано на рисунке 4.

Следует подчеркнуть, что равна 0 для всех τ ≠ о, т. е. две различные выборки БШ не коррелируют, вне зависимости от того, насколько близко они находятся.

Средняя мощность Р_ш белого шума бесконечна, так как бесконечна ширина полосы БШ. В природе БШ нет. Но он является хорошей моделью для исследования шума. Дельта-функция в уравнении для БШ означает, что БШ абсолютно не коррелирует с собственной смещенной версией для любого τ >0.

К сосредоточенным по спектру помехам принято относить сигналы посторонних радиостанций, преднамеренные помехи, излучения генераторов высокой частоты различного назначения (промышленных, медицинских) и т. п. В одних случаях эти колебания являются непрерывными (например, сигналы вещательных и телевизионных радиостанций), в других – они носят импульсный характер (сигналы радиотелеграфных станций и систем передачи данных). В отличии от флуктуационных ширина спектра сосредоточенной помехи в большинстве случаев не превышает полосы пропускания приемника, а в некоторых случаях она намного уже этой полосы. В диапазоне коротких волн сосредоточенные по спектру помехи являются основными, определяющими качество связи, и считаются случайными колебаниями с флуктуациями фаз и амплитуд (замираниями), распределение которых такое же, как у полезных сигналов.. личного назначения (промышленных, медицинских) и т. ий, преднамеренные помехи, излучения представлениям.

Выводы

1. Воздействие канала с аддитивным белым гауссовским шумом (АБГШ) на процесс обнаружения состоит в том, что шум независимо воздействует на каждый переданный символ. Такой канал называется каналом без памяти.

2. Сосредоточенные помехи – это помехи у которых ширина спектра соизмерима с шириной спектра сигнала или уже его.

Квантовый шум

Изобретение в 1959….1961 гг. когерентных лазерных источников света положило начало разработкам оптических линий связи, где переносчиком сообщений являются световые волны. Для световых волн диапазона 10 14 – 10 15 Гц (0,5….10,6 мкм) были созданы специальные направляющие системы – световоды. Наиболее перспективными из них оказались диэлектрические волноводы, или волокна, как их называют из-за малых поперечных сечений. Простейший световод представляет собой тонкое волокно цилиндрической формы, которое состоит из сердечника и оболочки. По сердечнику передаётся электромагнитная энергия в виде световой волны, поэтому его изготавливают из материала с наименьшими оптическими потерями (кварц, многокомпонентные стёкла)

В оптическом диапазоне заметно проявляется шум, связанный с дискретной природой электромагнитного излучения – квантовый шум (КШ).

Каналы связи, в которых КШ ограничивает качество приёма сообщений, называются квантовыми каналами.

Для каналов с открытым пространством основными перспективными направлениями стали космическая связь с использованием искусственных спутников земли (ИСЗ), ближняя наземная связь через атмосферу, подводная связь. Применяют газовые, твёрдотельные и полупроводниковые лазеры как видимого, так и инфракрасного диапазонов. В основном используют модуляцию с изменением интенсивности излучения – двоичную АМ, двоичную БИМ (биимпульсный сигнал), многопозиционную ВИМ. Успешно применяют и поляризационную модуляцию (ПМ). В многоканальных системах кроме временного используют и частотное разделение на поднесущих. Интенсивность модулируется гармоническими поднесущими (обычно СВЧ диапазона), которые модулируются по амплитуде, фазе или частоте.

Демодуляция чаще всего выполняется с прямым детектированием. В инфракрасном диапазоне с успехом применяют и гетеродинный приём. В каналах с закрытым пространством оптический сигнал канализируется либо по трубам – световодам с дискретными фазокорректорами (линзы, зеркала), либо по диэлектрическим волоконным световодам.

В последние годы основным направлением стала разработка волоконно-оптических каналов с передачей сигналов в ближнем инфракрасном (длина волны примерно 1 мкм) диапазоне. В качестве генераторов излучения применяются полупроводниковые лазеры и некогерентные источники – светодиоды.

Основные отличия оптических каналов, связанные с малой длиной волны и квантовой природой излучения, заключаются в следующем:

Тепловой шум может быть пренебрежительно мал;

Вследствие квантовых закономерностей параметры сигнала являются случайными, даже в отсутствие мешающих факторов.

В системе с пассивной паузой в пренебрежении тепловыми шумами символ 0 (отсутствие излучения) принимается безошибочно. Тогда как символ 1 (импульс излучения) с ненулевой вероятностью пропускается.

Вследствие высокой частоты несущих колебаний оказываются практически нереализуемыми согласованная фильтрация по частотному спектру и согласованная пространственная селекция сигнала, не выполняется разделение ортогональных сигналов.

Энергия электромагнитного поля имеет дискретную природу – излучается и поглощается квантами ,

Квантовый шум – это флуктуации измеряемых параметров сигнала.

Квантовый шум не аддитивен, так как он коррелирован с сигналом.

В области инфракрасного и видимого излучений энергия фотона увеличивается, а спектральная плотность средней мощности тепловых флуктуаций уменьшается.

Выводы

1. Шум лазера – это квантовый шум, так как проявляется во флуктуациях параметров сигнала, детерминированного по классическим представлениям.

2. Квантовый шум не является аддитивным, так как зависит от самого полезного сигнала.

Заключение

1. В каналах связи присутствуют помехи, которые ухудшают верность приёма сообщений.

2. Помехи могут быть аддитивными и мультипликативными.

3. Среди аддитивных помех наиболее распространенными являются флуктуационные, сосредоточенные по спектру и импульсные.

4. Удобной моделью аддитивной помехи является белый шум, с помощью которого можно описывать реальные процессы, происходящие в каналах связи.

5. Квантовый шум не является аддитивным, так как зависит от самого полезного сигнала.

Литература

1. Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.

1. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.

2. Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.

3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.

4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.

Источник

БОРЬБА С ФЛУКТУАЦИОННЫМИ, СОСРЕДОТОЧЕННЫМИ И ИМПУЛЬСНЫМИ ПОМЕХАМИ.

ФЛУКТУАЦИОННЫЕ ПОМЕХИ

Борьба с флуктуационными помехами (шумами) является од­ной из центральных задач обеспечения помехоустойчивости систем радиосвязи. Флуктуационные помехи всегда присутствуют в канале радиосвязи и их невозможно полностью подавить из-за их физической природы. Выбросы флуктуационной помехи могут иметь значительную величину и ее порой трудно отличать от сиг­нала, даже в его отсутствие. Сдругой стороны, интерференция сигнала и помехи может привести к тому, что суммарное колебание окажется ниже порога регистрации и сигнал не будет зафик­сирован.

Для борьбы с флуктуационными помехами может использоваться любой из методов, рассмотренных в главе 4.2. Однако ниже остановимся главным образом на тех методах борьбы с флуктуационными помехами, которые позволяют увеличить среднюю мощность сигнала, поскольку качество связи определяется отношением средней мощности сигнала к мощности шума в полосе пропускания приемника.

Известно, что при передаче непрерывных сигналов средняя мощность передатчика оказывается значительно ниже максималь­ной. Самым очевидным способом повышения средней мощности сигнала в этом случае является сокращение динамического диапазона сигнала. Этого можно достичь путем преобразования не­прерывных сигналов в цифровые, а применительно к речевым сигналам, еще и клипированием или компандированием сигнала (см. главу 3.1.2).

В реальных средствах радиосвязи наиболее распространенным методом борьбы с флуктуационными помехами является фильтрация сигналов. Ниже остановимся на отыскании оптимальных условий фильтрации дискретных и непрерывных сигналов.

При фильтрации дискретных сигналов u_c1(t) и u_c2(t), которые могут представлять двоичный сигнал, условие оптимального приема при действии флуктуационных помех будет определяться неравенством [2]:

. (4.6)

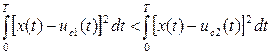
Выражение (4.6) можно преобразовать к эквивалентному не­равенству, если выполнить операцию возведения в квадрат подын­тегральных выражений

,(4.7)

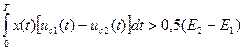
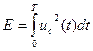
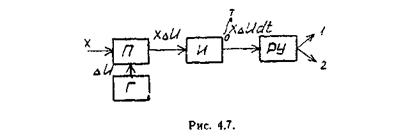
где — энергия сигнала.

Условие (4.7) можно реализовать с помощью схемы так на­зываемого оптимального порогового приемника (рис. 4.7).

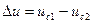
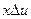
Принимаемое колебание и разностный сигнал перемножаются (П), после чего результат интегриру­ется (И) и сравнивается с постоянным порогом, равным 0,5 (E₂-E₁).

Оптимальный пороговый приемник проще приемника В. А. Котельникова и его целесообразно применять в каналах с ад­дитивными помехами. В каналах же с переменными параметра­ми, где уровень сигнала все время изменяется, необходимо порог автоматически регулировать, что является недостатком.

При равенстве энергий сигналов (Е₂ = Е₁) этот недостаток устраняется, поскольку порог равен нулю и решающее устройст­во РУ выдает только лишь знак сигнала.

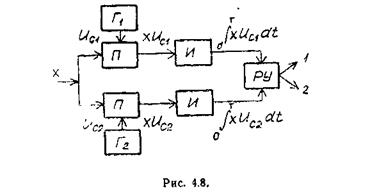
Следует заметить, что в случае E₂=E₁ в приемнике В. А. Котельникова отпадает необходимость в операции квадратирования и он преобразуется в корреляционный когерентный приемник (рис. 4.8), реализующий следующий алгоритм работы:

.(4.8)

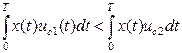
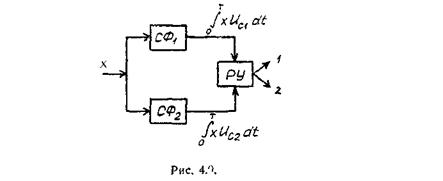
Условие (4.8) можно также реализовать с помощью опти­мального приемника на согласованных фильтрах (рис. 4.9).

При отсутствии помех сигнал на выходе каждого согласован­ного фильтра с точностью до постоянного множителя совпадает с автокорреляционной функцией входного сигнала. При наличии помех напряжение на выходе каждого согласованного фильтра будет пропорционально функции взаимной корреляции принятого сигнала x(t) и переданного сигнала u_c(t).

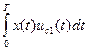
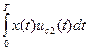
Первый согласованный фильтр СФ1 выполняет операцию , а второй согласованный фильтр СФ2 — операцию , после чего напряжение с выхода каждого фильтра поступает на решающее устройство РУ.

Величина отклика на выходе согласованного фильтра и на выходе коррелятора при когерентном приеме одинакова и рав­на [3, 5].

. (4.9)

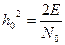
Из (4.9) следует, что отношение сигнал/шум на выходе опти­мального приемника не зависит от формы входного сигнала и ее можно выбирать из условия обеспечения наиболее эффективной борьбы с другими видами помех.

По существу, согласованный фильтр эквивалентен коррелято­ру. Однако реализовать согласованный фильтр, особенно для ШПС, труднее, чем коррелятор.

На практике при приеме дискретных сигналов широко исполь­зуется квазиоптимальная фильтрация, когда в приемнике приме­няются фильтры, согласованные с сигналом лишь по полосе. В случае приема узкополосных дискретных сигналов длительностью Т_с в зависимости от формы сигнала необходимо правильно выбирать амплитудно-частотную характеристику фильтра. Это имеет важное значение для получения максимального отношения сигнал/шум на его выходе. Сказанное иллюстрируется таблицей 4.1, в которой для различных по форме сигналов и АЧХ фильт­ров приведены максимальные нормированные значения отноше­ния сигнал/шум 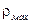на выходе согласованных по полосе фильт­ров.

Вид огибающей сигнала	ЛЧХ фильтра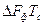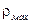
Прямоугольная Прямоугольная Гауссова Гауссова	Прямоугольная Гауссова Прямоугольная Гауссова	1,37 0.72 0.72 0,63	0,91 0,94 0.94 1,0

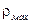
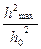
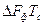
В таблице 4.1 = — отношение сигнал/шум на выходе фильтра, согласованного на полосе с сигна­лом, а h 2 ₀ отношение сигнал/шум на выходе согласованного фильтра. Оптимальная полоса фильтра находится из соотношения

.

Из таблицы 4.1 видно, что при равенстве центральных час­тот сигнала и фильтра отношение сигнал/шум на входе решаю­щей схемы при квазиоптимальной фильтрации по сравнению с оп­тимальной фильтрацией снижается незначительно. В то же время реализовать фильтр, согласованный с сигналом по полосе, зна­чительно проще, чем согласованный фильтр. Этим, в частности, можно объяснить широкое применение в средствах радиосвязи фильтров, согласованных с сигналом только по полосе.

Рассмотрим некоторые особенности оптимального приема не­прерывных сигналов при действии флуктуационных помех.

В главе 4.2 уже отмечалось, что оптимальная линейная фильтрация непрерывных сигналов базируется на теории Колмо­горова-Винера, которая верна лишь для стационарных случайных процессов. Однако реальные непрерывные сигналы (телефонные,телеметрические, телевизионные и др.) не всегда являются ста­ционарными, что не позволяет решить задачу построения опти­мальных линейных фильтров на базе теории линейной фильтра­ции. В связи с этим на практике находят применение другие способы построения оптимальных приемников непрерывных сиг­налов.

Если бы передаваемый непрерывный сигнал был полностью известным, подобно тому, как это имеет место при передаче дис­кретных сигналов, то схемы оптимальных приемников для не­прерывных сигналов не отличались бы от рассмотренных выше схем оптимальных приемников. Однако при передаче непрерывных сигналов получатель информации находится в более тяжелых ус­ловиях, поскольку он располагает лишь некоторой информацией о сигнале. Ему могут быть известны рабочая частота, вид моду­ляции, ширина спектра сигнала и т. п. Остальную же информа­цию он должен получить путем анализа принятого сигнала за не­который предшествующий промежуток времени Т.

Анализ принятого колебания x(t) должен способствовать вос­произведению переданного сигнала u_c(t) с минимальным среднеквадратическим отклонением.

Нахождение плотности распределения вероятностей основано на вычислении взаимной корреляции между принятым колебанием x(t) и переданным ожидаемым сигналом u_c(t). Плотность рас­пределения вероятностей можно представить функцией [2]

,(4.10)

где N₀ — постоянная спектральная плотность шума.

Так как сигнал u_c(t) неизвестен, то вместо сигнала следу­ет брать некоторое его оценочное значение v(t), которое в резуль­тате анализа колебания x(t) полагается близким к переданному сигналу. Поэтому приемник определяет не функцию h(u), а не­которую оценочную эквивалентную ей функцию h(v).

Поясним это положение. Если бы сигнал был полностью из­вестен, как это имело место при приеме дискретных сообщений, то с помощью коррелятора или оптимального фильтра была бы найдена именно функция h(u). При передаче же непрерывных со­общений сигнал известен не полностью. Могут быть известны, как уже отмечалось, только некоторые его параметры, такие, как ра­бочая частота, вид модуляции, ширина спектра и некоторые другие. Сам же передаваемый сигнал неизвестен. При этом сиг­нал меняется непрерывно со временем и может принять любую форму. Наблюдая за принятым колебанием x(t) за предшеству­ющий промежуток Т, приемник должен произвести оценку этого сигнала и вычислить оценочную функцию

, (4.11)

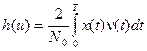
где v(t) — оценочное значение передаваемого сигнала на выхо­де приемника.

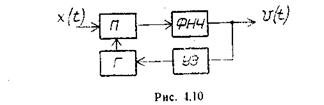
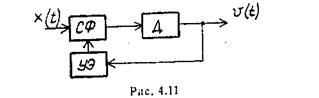
Для нахождения h(v) можно воспользоваться либо схемой следящего коррелятора (рис. 4.10), либо схемой, содержащей следящий фильтр, т. е. фильтр с переменными параметрами (рис. 4.11). Обе схемы имеют информационный канал, на выходе кото­рого формируется оценочное значение v(t) передаваемого сигна­ла u_с (t), а также канал обратной связи.

В схеме следящего коррелятора (рис. 4.10) обратный канал, содержащий управляющий элемент УЭ и генератор Г, служит для формирования опорного сигнала, подаваемого на перемножитель П, на вход которого поступает колебание x(t). Управляющий элемент служит для изменения модулируемого параметра рабо­чей частоты, формируемой генератором Г, в соответствии с ве­личиной v(t). Фильтр нижних частот ФНЧ используется в качест­ве интегратора на интервале наблюдения 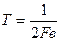(F_в — верхняя частота в спектре передаваемого сигнала).

В схеме со следящим фильтром (рис. 4.11) посредством об­ратного канала, содержащего УЭ, изменяются параметры фильт­ра СФ в соответствии со значением v(t). Поскольку величина v(t) непрерывно меняется, то и параметры фильтра также непре­рывно изменяются, подстраиваясь под ожидаемый сигнал u_с(t).

Следящие оптимальные приемники являются нелинейными устройствами, поэтому теорию оптимального приема непрерывных сигналов следует рассматривать как теорию оптимальной нели­нейной фильтрации.

Следует отметить, что при действии в канале связи как ад­дитивной, так и мультипликативной помехи приемники, приве­денные на рис. 4.10 и 4.11, должны быть дополнены системами автоматической регулировки усиления и фазовой автоподстройкой частоты, а при изменяющейся величине N₀ — устройством изме­рения и выравнивания помех.

Таким образом, при оптимальном приеме сигналов, передава­емых по каналам с переменными параметрами и непостоянным уровнем помех, в приемнике должно автоматически осуществ­ляться непрерывное слежение за формой сигнала и характером помехи, а это значит, что оптимальный приемник должен быть адаптивным.

СОСРЕДОТОЧЕННЫЕ ПОМЕХИ

В каналах радиосвязи кроме флуктуационной помехи с пос­тоянной спектральной плотностью N₀ имеют место помехи, энер­гия которых сосредоточена в некоторой полосе частот. Помехи такого рода называются сосредоточенными по спектру. Они соз­даются всевозможными внешними источниками (соседними ра­диостанциями, генераторами помех и т. п.), а также могут по­рождаться каналом связи. Сосредоточенная помеха представляет собой колебание вида (4.4). Длительность сосредоточенной по спектру помехи Т_п может быть произвольной. Если Т_п, Т_с то основная энергия помехи сконцентрирована в полосе частот, меньшей или соизмеримой с полосой сигнала. При Т_п 0 К с учётом эффективной полосы пропускания приёмника ΔF_эф=200 кГц.

1. Считать в полосе пропускания приёмника спектральную плотность помехи постоянной.

По радиоканалу с флуктуационными помехами передаётся сигнал длительностью Т_с=20 мс и мощностью Р_с=1 Вт.

Найти величину отклика на выходе коррелятора при когерентном приёме, если эффективная полоса приёмника ΔF_эф=1 кГц, а мощность помехи Р_п=10 мВт.

Источник