Чем отличается принцип записи многозначных чисел в римской и арабской системах счисления
Интересный факт!
Интересно, любопытно, удивительно
Римские и арабские цифры. Происхождение и написание. Видео.
Posted by: admin | on Ноябрь 25, 2013
Дорогие друзья!
Сегодня нас нисколько не удивляют встречающиеся в текстах римские и арабские цифры (Пётр I, 2013 год). Они мирно соседствуют рядом, стали для всх привычными. Но давайте поговорим про их происхождение и написание (видео).
Римские цифры.
Римские цифры возникли ещё за полвека до наступления новой эры, и в основу их графического написания было положено изображение пальцев руки и самой ладони, поскольку именно руки были первым инструментом для счёта.
Римские числа именно так и записываются: если меньшая по значению цифра находится слева от большей – она вычитается из неё IX (то есть,10-1=9), а если она стоит справа от большей, то прибавляется XI (10 + 1 =11).
Для этого нужно знать не только обозначение единицы и десятка, а также сотен и тысяч.
А чтобы не забыть обозначения римских цифр, используется следующая памятка:
М — Мы D — дарим С — сочные L — лимоны, Х — хватит V — всем I — их.
Дорогие друзья, с наступающим Вас ММXIV годом!
Арабские цифры.
Арабы переняли те цифры, что называются теперь «арабскими» у индусов, а европейцы уже заимствовали эти цифровые символы у арабов в конце средневековья.
Само слово «цифра» пришло к нам также из арабского языка.
Существует одна из гипотез, что некий арабский математик древности предложил связать количество углов написанной цифры с её числовым значением.
Очертания всех арабских цифр состояли из отрезков, при соединении дававших определённое количество углов.
Не имеет углов только цифра «ноль» (придуманная гораздо позже остальных цифр), поэтому она единственная изображается в виде овала.
Итак, арабские цифры выглядят следующим образом (напоминают написание индекса на конвертах):
0 — цифра не имеет углов;
1 — имеет один угол;
2 — имеет два угла;
3 — имеет три угла;
4 — содержит четыре угла, два из которых прямые;
5 — имеет пять прямых углов;
6 — имеет шесть прямых углов;
7 — имеет семь острых и прямых углов;
8 — имеет восемь прямых углов;
9— имеет девять прямых углов.
Со временем исчезла необходимость каждый раз считать количество углов, чтобы определить обозначаемое цифрой количество; очертания цифр приобрели более округлый вид, и уже много веков весь мир использует их для записи чисел.
Видео.
На этом интересный факт исчерпал себя!
Но завтра найдём что-нибудь более интересное!
С наилучшими пожеланиями здоровья и благоденствия,
Ваш преданный гид по Миру Интересных Фактов,
XXX 333
Первое — римское тридцать, второе — арабское триста тридцать три. И задайте вопрос: «Чем отличается принцип записи многозначных чисел римскими и арабскими цифрами?» Скорее всего, вы сразу не услышите тот ответ, который бы хотели получить. Тогда, указывая на отдельные цифры римского числа, спрашивайте: «Что (какое количество) обозначает эта цифра?» Получите ответ: «Десять!» — «А эта цифра?» — «Десять!» — «А эта?» — «Десять» — «Как получается значение данного трехзначного числа?» — «Десять прибавить десять, прибавить десять, получается тридцать!» « А теперь переходим к числу 333. Снова задаем вопросы: «Какое количество в записи числа обозначает первая цифра справа?» — «Три единицы!» — «А вторая цифра?» — «Три десятка!» — «А третья цифра?» — «Три сотни!» — «А как получается общее значение числа»— «К трем единицам прибавить три десятка и прибавить три сотни получится триста тридцать три!»
Из этого диалога следуют все правила, которые учитель должен сообщить ученикам. В римском способе записи чисел значение, которое несет каждая цифра в числе, не зависит от позиции этой цифры. В арабском же способе значение, которое несет каждая цифра в записи числа, зависит не только от того, какая это цифра, но и от позиции, которую она занимает в числе. Сделав 
ударение на слове «позиция», учитель сообщает, что римский способ записи чисел называется непозиционным, а арабский — позиционным. После этого можно ввести термин «система счисления».
Система счисления — это определенный способ представления чисел и соответствующие ему правила действия над числами.
Теперь нужно дать понять ученикам, что позиционных систем счисления существует множество, и отличаются они друг от друга алфавитом — множеством используемых цифр. Размер алфавита (число цифр) называется основанием системы счисления. Задайте вопрос: «Почему арабская система называется десятичной системой счисления?» Наверняка услышите в ответ про десять цифр в алфавите. Делаем вывод: основание арабской системы счисления равно десяти, поэтому она называется десятичной.
Следует показать алфавиты различных позиционных систем счисления. Системы с основанием не больше 10 используют только арабские цифры. Если же основание больше 10, то в роли цифр выступают латинские буквы в алфавитном порядке.
Далее нужно научить учеников записывать натуральный ряд чисел в различных позиционных системах. Объяснение следует проводить на примере десятичной системы, для которой вид натурального ряда чисел им хорошо известен:
По такому же принципу строится натуральный ряд и в других системах счисления. Например, в четверичной системе (с основа-4):
Для указания на основание системы, к которой относится число, вводим индексное обозначение. Например, 368 указывает на это число в восьмеричной системе счисления, Следует подчеркнуть, что в любой системе счисления ее основание записывается как 10.
Еще одно важное замечание: ни в коем случае нельзя называть недесятичные числа так же, как десятичные. Например, нельзя называть восьмеричное число 368 как тридцать шесть! Надо говорить: «Три —шесть»
Сущность позиционного представления чисел отражается в форме записи чисел. Снова для объяснения привлекаем десятичную систему.
Последнее выражение и называется развернутой формой записи числа.
Поскольку нам хорошо знакома лишь десятичная арифметика, то любой перевод следует свести к выполнению вычислений над десятичными числами.
Объяснение способов перевода следует начать с перевода десятичных чисел в другие системы счисления. Делается это просто нужно перейти к записи развернутой формы числа в десятичной системе.
1753 8 = (1 *10 3 + 7* 10 2 + 5* 10 1 + 3)8 = ( 1 * 8 3 + 7 * 8 2 + 5 * 8 1 + 3)10
Для вычисления значения числа по его развернутой форме записи существует удобный прием, который называется вычислительной схемой Горнера. Суть его состоит в том, что развернутая запись числа преобразуется в эквивалентную форму с вложенными скобками. Например, для рассмотренного выше восьмеричного числа это выглядит так:
17538 = (1х8 3 + 7х8 2 + 5х8 1 + 3)10 = ((1×8 + 7)х8 + 5)х8 + 3
Нетрудно понять, что если раскрыть скобки, то получится то же самое выражение.
Перевод десятичных чисел в другие системы счисления — задача более сложная. В принципе, все происходит через ту же самую развернутую форму записи числа.. Только теперь нужно суметь десятичное число разложить в сумму по степеням нового основания п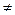 
10. Например, число 8510 по степеням двойки раскладывается так:
8510 = 1х2 6 + 0х2 5 + 1х2 4 + 0х2 3 + 1×2 2 + 0x2 + 1= 10101012.
В рамках минимального объема базового курса не обязательно изучать приемы перевода дробных десятичных чисел в другие системы счисления.
Применение двоичной системы счисления в ЭВМ может рассматриваться в двух аспектах:
1) двоичная нумерация;
2) двоичная арифметика, т. е. выполнение арифметических вычислений над двоичными числами. С двоичной нумерацией ученики встретятся в теме «Представление текста в компьютерной памяти». Рассказывая о таблице кодировки ASCII, учитель должен сообщить ученикам, что внутренний двоичный код символа — это его порядковый номер в двоичной системе счисления.
В рамках базового курса достаточно ограничиться рассмотрением вычислений с целыми двоичными числами. Приемы выполнения вычислений с многозначными числами в двоичной системе аналогичны десятичной. Иначе говоря, процедуры вложения, вычитания и умножения «столбиком» и деления «уголком» в двоичной системе производятся так же, как и в десятичной.
В базовом курсе можно не рассматривать сложные примеры деления многозначных двоичных чисел. Хотя способные ученики могут справиться и с ними, поняв общие принципы.
Существует простая связь между двоичным и шестнадцатеричным представлением числа. При переводе числа из одной системы в другую, одной шестнадцатеричной цифре соответствует 4 – разрядный двоичный код. Это соответственно отражено в двоично-шестнадцатеричной таблице.
Преимущество 16-ричного представления состоит в том, что оно в 4 раза короче двоичного.
Рассматривая структуру памяти компьютера, принципы адресации байтов памяти, можно обсудить с учениками следующий вопрос: как связан диапазон адресов с разрядностью адреса.
Примеры решения задач
Ниже рассмотрены решения некоторых задач, взятых из Семакина Задачник практикум
Пример 1. Перевести в десятичную систему числа: 2213; Е41
Е41А,1216 =((14х16 + 4)х1б+ 1)х1б + 10+ (2/16 + 1)/16 = 58394 + 0,0703125 = 58394,070312510.
Пример 2. Перевести шестнадцатеричные числа в восьмеричную систему.
Конечно, такой перевод можно производить рез десятичную систему по схеме 16 => 10 => 8. Но это долго и неудобно. Лучше выполнять такой перевод по схеме 16 => 2 => 8. В этом случае ничего не требуется вычислять, все сводится к формальной перекодировке. На втором шаге следует сгруппировать двоичные цифры тройками.
Пример 3. Найти основание р системы счисления и цифру n если верно равенство: 33m5n + 2n443 = 55424. Пример выполнен в системе счисления с основанием р, т — максимальная цифрам этой системе. Решение. Запишем столбиком данное сложение:
8.3. языки представления чисел: системы счисления
8.3. языки представления чисел: системы счисления
Подходы к раскрытию темы в учебной литературе
Тема «Системы счисления» имеет прямое отношение к математической теории чисел. Однако в школьном курсе математики она, как правило, не изучается. Необходимость изучения этой темы в курсе информатики связана с тем фактом, что числа в памяти компьютера представлены в двоичной системе счисления, а для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную системы. Это одна из традиционных тем курса информатики или программирования. Являясь смежной с математикой, данная тема вносит вклад также и в фундаментальное математическое образование школьников.
В первом учебнике информатики [18] понятие системы счисления не упоминается совсем. Говорится лишь о том, что вся информация в компьютере представляется в двоичном виде. То же самое можно сказать и про учебник [17]. Среди учебников второго поколения наибольшее внимание системам счисления уделено в книге [6]. Этой теме посвящен отдельный параграф, где дано следующее определение «Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр)». В более позднем учебнике этих же авторов [7] приводится такое определение: «Способ записи чисел называется нумерацией или, по-другому, системой счисления».
Если рассматривать систему счисления как язык представления числовой информации, то можно сказать, что данные выше определения затрагивает только алфавит, синтаксис и семантику языка чисел. Более полное определение дано в [24]: «Система счисления — способ изображения чисел и соответствующие ему правила действия над числами». Под правилами действия понимаются способы выполнения арифметических вычислений в рамках данной системы счисления. Эти правила можно назвать прагматикой языка чисел.
Среди школьных учебников самое подробное изложение темы «Системы счисления» дается в [9]. В качестве дополнительной литературы, раскрывающей данную тему наиболее полно, можно рекомендовать учебное пособие [1].
Методические рекомендации по изучению темы
ª Позиционные и непозиционные системы счисления.
ª Основные понятия позиционных систем: основание, алфавит.
ª Развернутая форма представления чисел в позиционных системах.
ª Перевод чисел из одной системы в другую.
ª Особенности двоичной арифметики.
ª Связь между двоичной и шестнадцатеричной системами.
Ученики, безусловно, знакомы с записью чисел как римскими, так и арабскими цифрами. Они привыкли видеть римские цифры в обозначении глав в книге, в указании столетий (XX в.) и в некоторых других нумерациях. Математические расчеты они всегда производили в арабской системе чисел. В данной теме учителю предстоит раскрыть перед учениками эти, казалось бы, знакомые вещи с новой стороны.
С методической точки зрения бывает очень эффективным прием, когда учитель подводит учеников к самостоятельному, пусть маленькому, открытию. В данном случае желательно, чтобы ученики сами подошли к формулировке различия между позиционным и непозиционным принципом записи чисел. Сделать это можно, отталкиваясь от конкретного примера. Напишите на доске два числа:
Первое — римское тридцать, второе — арабское триста тридцать три. И задайте вопрос: «Чем отличается принцип записи многозначных чисел римскими и арабскими цифрами?» Скорее всего, вы сразу не услышите тот ответ, который бы хотели получить. Тогда, указывая на отдельные цифры римского числа, спрашивайте: «Что (какое количество) обозначает эта цифра?» Получите ответ: «Десять!» — «А эта цифра?» — «Десять!» — «А эта?» — «Десять» — «Как получается значение данного трехзначного числа?» — «Десять прибавить десять, прибавить десять, получается тридцать!» А теперь переходим к числу 333. Снова задаем вопросы: «Какое количество в записи числа обозначает первая цифра справа?» — «Три единицы!» — «А вторая цифра?» — «Три десятка!» — «А третья цифра?» — «Три сотни!» — «А как получается общее значение числа?» — «К трем единицам прибавить три десятка и прибавить три сотни получится триста тридцать три!»
Из этого диалога следуют все правила, которые учитель должен сообщить ученикам. В римском способе записи чисел значение, которое несет каждая цифра в числе, не зависит от позиции этой цифры. В арабском же способе значение, которое несет каждая цифра в записи числа, зависит не только от того, какая это цифра, но и от позиции, которую она занимает в числе. Сделав ударение на слове «позиция», учитель сообщает, что римский способ записи чисел называется непозиционным, а арабский — позиционным. После этого можно ввести термин «система счисления».
Система счисления — это определенный способ представления чисел и соответствующие ему правила действия над числами.
Римский способ записи чисел является примером непозиционной системы счисления, а арабский — это позиционная система счисления.
Следует подчеркнуть связь между способом записи чисел и приемами арифметических вычислениц в соответствующей системе счисления. Предложите ученикам выполнить умножение, например, числа сто тридцать четыре на семьдесят шесть, используя римскую и арабскую системы счислений! С арабскими числами они легко справятся, а также смогут убедиться, что римские цифры — не помощники в вычислениях. В римской системе нет простых и понятных правил выполнения вычислений с многозначными числами. Для арабской системы такие правила известны еще с IX в. В этой теме полезно рассказать ученикам, что правила выполнения вычислений с многозначными числами были разработаны выдающимся математиком средневекового Востока Мухамедом аль-Хорезми и в Европе были названы алгоритмами (от латинского написания имени аль-Хорезми — Algorithm!). Этот факт следует напомнить позже, при изучении алгоритмизации. Итак, именно позиционные системы счисления стали основой современной математики. Далее, как и в математике, в информатике мы будем иметь дело только с числами в позиционных системах счисления.
Теперь нужно дать понять ученикам, что позиционных систем счисления существует множество, и отличаются они друг от друга алфавитом — множеством используемых цифр. Размер алфавита (число цифр) называется основанием системы счисления. Задайте вопрос: «Почему арабская система называется десятичной системой счисления?» Наверняка услышите в ответ про десять цифр в алфавите. Делаем вывод: основание арабской системы счисления равно десяти, поэтому она называется десятичной.
Следует показать алфавиты различных позиционных систем счисления. Системы с основанием не больше 10 используют только арабские цифры. Если же основание больше 10, то в роли цифр выступают латинские буквы в алфавитном порядке. Из таких систем в дальнейшем будет рассматриваться лишь шестнадцатерич-ная система.
Далее нужно научить учеников записывать натуральный ряд чисел в различных позиционных системах. Объяснение следует проводить на примере десятичной системы, для которой вид натурального ряда чисел им хорошо известен:
Принцип построения ряда такой: сначала в порядке возрастания значений записываются все однозначные числа; первое двузначное число — всегда 10 (у многозначных целых чисел 0 впереди не является значащей цифрой и обычно не пишется). Далее следуют все двузначные сочетания единицы с другими цифрами; затем — двузначные числа, начинающиеся с 2, затем — с 3 и т. д. Самое большое двузначное число — 99. Затем идут трехзначные числа, начиная от 100 до 999 и т.д.
По такому же принципу строится натуральный ряд и в других системах счисления. Например, в четверичной системе (с основанием 4):
1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33, 100,
Аналогично и для других систем. Наибольший интерес представляет натуральный ряд двоичных чисел. Вот как он выглядит:
1, 10, 11, 100, 101, ПО, 111, 1000, 1001, 1010, 1011, 1100,
Следует обратить внимание учеников на быстрый рост числа цифр.
Для указания на основание системы, к которой относится число, вводим индексное обозначение. Например, 368 указывает на то, что это число в восьмеричной системе счисления, 1А6,6 — шестнадцатеричное число, 10112 — число в двоичной системе. Индекс всегда записывается десятичным числом. Следует подчеркнуть то, что в любой системе счисления ее основание записывается как 10.
Еще одно важное замечание: ни в коем случае нельзя называть недесятичные числа так же, как десятичные. Например, нельзя называть восьмеричное число 368 как тридцать шесть! Надо говорить: «Три — шесть». Или, нельзя читать 1012 как «сто один». Надо говорить «один — ноль — один». Следует также понимать, что, например, 0,12 — это не одна десятая, а одна вторая, или 0,18 — это одна восьмая и т. п.
Сущность позиционного представления чисел отражается в развернутой форме записи чисел. Снова для объяснения привлекаем десятичную систему. Например:
5319,12 = 5000 + 300 + 10 + 9 + 0,1 + 0,02 =
= 5´103 + 3´102 + 1´101 + 9 + 1´10-1 + 2´10-2.
Последнее выражение и называется развернутой формой записи числа. Слагаемые в этом выражении являются произведениями значащих цифр числа на степени десятки (основания системы счисления), зависящие от позиции цифры в числе — разряда. Цифры в целой части умножаются на положительные степени 10, а цифры в дробной части — на отрицательные степени. Показатель степени является номером соответствующего разряда. Аналогично можно получить развернутую форму чисел в других системах счисления. Например, для восьмеричного числа:
17538 = 1´103 + 7´102 + 5´101 + 3.
Следующий вопрос, изучаемый в этом разделе, — способы перевода чисел из одной системы в другую. Основная идея заключается в следующем: перевод чисел неизбежно связан с выполнением вычислений. Поскольку нам хорошо знакома лишь десятичная арифметика, то любой перевод следует свести к выполнению вычислений над десятичными числами.
Объяснение способов перевода следует начать с перевода десятичных чисел в другие системы счисления. Делается это просто: нужно перейти к записи развернутой формы числа в десятичной системе. Вот пример такого перехода для приведенного выше восьмеричного числа:
17538 = (1´103 + 7´102 + 5´101 + 3)8 = (1´83 +7´82 + 5´81+ 3)10.
Теперь нужно вычислить полученное выражение по правилам десятичной арифметики и получить окончательный результат:
17538 = (192 + 448 + 40 + 3)10 = 68310.
Чаще всего развернутую форму числа сразу записывают в десятичной системе. Вот еще пример с двоичным числом:
101101,12 =(1х25 + 0´24 + 1´23 + 1´22 + 0´21 + 1 + 1´2-1)10 = 32 + 8 + 4 + 1 + 0,5 = 45,510
Для вычисления значения числа по его развернутой форме записи существует удобный прием, который называется вычислительной схемой Горнера. Суть его состоит в том, что развернутая запись числа преобразуется в эквивалентную форму с вложенными скобками. Например, для рассмотренного выше восьмеричного числа это выглядит так:
17538 = (1´83 + 7´82 + 5´81 + 3)10 = ((1´8 + 7) ´8 + 5) ´8 + 3.
Нетрудно понять, что если раскрыть скобки, то получится то же самое выражение. В чем же удобство скобочной структуры? А в том, что ее вычисление производится путем выполнения последовательной цепочки операций умножения и сложения в порядке их записи слева направо. Для этого можно использовать самый простой калькулятор (без памяти), поскольку не требуется сохранять промежуточные результаты. Схема Горнера сводит вычисление таких выражений к минимальному числу операций.
Перевод десятичных чисел в другие системы счисления — задача более сложная. В принципе, все происходит через ту же самую развернутую форму записи числа. Только теперь нужно суметь десятичное число разложить в сумму по степеням нового основания п Ф 10. Например, число 85,0 по степеням двойки раскладывается так:
8510 = 1´26 + 0´25 + 1´24 + 0´23 + 1´22 + 0´2 + 1 = 10101012.
Однако проделать это в уме довольно сложно. Здесь следует показать формальную процедуру (алгоритм) такого перевода. Описание алгоритма можно прочитать в учебнике [9] или пособии [1]. Там же дается математическое обоснование алгоритма. Разбор этого обоснования требует от учеников определенного уровня математической грамотности и возможен в варианте углубленного изучения базового курса.
В рамках минимального объема базового курса не обязательно изучать приемы перевода дробных десятичных чисел в другие системы счисления. При знакомстве с этим вопросом в углубленном курсе нужно обратить внимание на следующее обстоятельство: десятичные дроби с конечным числом цифр при переводе в другие системы могут превратиться в бесконечные дроби. Если удается найти период, тогда его следует выделить. Если же период не обнаруживается, то нужно договориться о точности (т.е. о количестве цифр), с которой производится перевод.
Если ставится цель получения при переводе дробного числа наиболее близкого значения, то, ограничивая число знаков, нужно производить округления. Для этого в процессе перевода следует вычислять на одну цифру больше, а затем, применяя правила округления, сокращать эту цифру. Выполняя округление, нужно соблюдать следующее правило: если первая отбрасываемая цифра больше или равна n/2 (п — основание системы), то к сохраняемому младшему разряду числа прибавляется единица. Например, округление восьмеричного числа 32,324718 до одного знака после запятой даст в результате 32,3; а округление до двух знаков после запятой — 32,33.
Математическая суть отмеченной выше проблемы связана со следующим фактом: многие дробные рациональные десятичные числа в других системах счисления оказываются иррациональными.
Применение двоичной системы счисления в ЭВМ может рассматриваться в двух аспектах: 1) двоичная нумерация; 2) двоичная арифметика, т. е. выполнение арифметических вычислений над двоичными числами. С двоичной нумерацией ученики встретятся в теме «Представление текста в компьютерной памяти». Рассказывая о таблице кодировки ASCII, учитель должен сообщить ученикам, что внутренний двоичный код символа — это его порядковый номер в двоичной системе счисления.
Практическая потребность знакомства с двоичной арифметиrой возникает при изучении работы процессора (см., например, [9, гл. 11]). В этой теме рассказывается, как процессор ЭВМ выполняет арифметические вычисления. Согласно принципу Дж. фон Неймана, компьютер производит вычисления в двоичной системе счисления. В рамках базового курса достаточно ограничиться рассмотрением вычислений с целыми двоичными числами.
Для выполнения вычислений с многозначными числами необходимо знать правила сложения и правила умножения однозначных чисел. Вот эти правила:
Принцип перестановочности сложения и умножения работает во всех системах счисления. Далее следует сообщить, что приемы выполнения вычислений с многозначными числами в двоичной системе аналогичны десятичной. Иначе говоря, процедуры сложения, вычитания и умножения «столбиком» и деления «уголком» в двоичной системе производятся так же, как и в десятичной.
Рассмотрим правила вычитания и деления двоичных чисел. Операция вычитания является обратной по отношению к сложению. Из приведенной выше таблицы сложения следуют правила вычитания:
А вот пример вычитания многозначных чисел:
Полученный результат можно проверить сложением разности с вычитаемым. Должно получиться уменьшаемое число.
Деление — операция обратная умножению. В любой системе счисления делить на 0 нельзя. Результат деления на 1 равен делимому. Деление двоичного числа на 102 ведет к перемещению запятой на один разряд влево, подобно десятичному делению на десять. Например:
10010:10 = 1001; 1011:10 = 101,1; 101100:10 = 10110.
Деление на 100 смещает запятую на 2 разряда влево и т.д. В базовом курсе можно не рассматривать сложные примеры деления многозначных двоичных чисел. Хотя способные ученики могут справиться и с ними, поняв общие принципы.
Представление информации, хранящейся в компьютерной памяти в ее истинном двоичном виде весьма громоздко из-за большого количества цифр. Имеется в виду запись такой информации на бумаге или вывод ее на экран. Для этих целей принято использовать восьмеричную или шестнадцатеричную системы счисления. В современных ПК чаще всего используется шестнадцатеричная система.
Существует простая связь между двоичным и шестнадцатерич-ным представлением числа. При переводе числа из одной системы в другую, одной шестнадцатеричной цифре соответствует 4-разрядный двоичный код. Это соответствие отражено в двоично-шестнадцатеричной таблице: