Чем отличается ооф и одз

14.04.202214.04.2022 admin 0 Comments

Область определения и область значений функции

Областью определения числовой функции (ООФ) называется множество числовых значений, которые может принимать аргумент x, так чтобы функция имела смысл.

ООФ – это основная характеристика любой функции, с учетом которой исследуются все остальные характеристики;

ООФ находится чаще всего как подмножество X множества действительных чисел , на котором выполнимы все операции, определяющие значение функции y по значению ее аргумента x; в этом случае ООФ называют естественной областью определения функциии она совпадает с областью допустимых значений (ОДЗ) для пенременной в выражении f(x);

ООФ может находиться по смыслу функции и в этом случае она будет более узкой, чем естественная ООФ;

приняты и другие обозначения ООФ, например, D(f) или D(y).

Областью значений числовой функции (ОЗФ) называется множество числовых значений, которые принимает функция y, если ее аргумент .

ОЗФ – это вспомогательная характеристика функции, которая вполне определяется после построения графика функции. До того, как график построен, ОЗФ может быть найдена только в отдельных случаях, когда это помогают сделать известные свойства основных элементарных функций, с помощью которых записана исследуемая функция. Для ОЗФ приняты также обозначения E(f) или E(y).

Пример (нахождение ООФ и ОЗФ)

Найти область определения и область значений в каждой из следующих функций:

1) ООФ: или ;

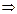
ОЗФ: , так как это сложная функция, полученная суперпозицией двух функций : и ;

2) ООФ: ;

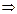
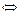
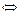
ООФ записана из ограничения по делению: на ноль делить нельзя;

ОЗФ можно найти только после построения графика функции;

3) ООФ: ;

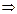
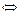
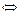
ООФ определена операцией извлечения корня квадратного, которая имеет смысл только для неотрицательных чисел;

ОЗФ: , так как корень квадратный принимает все неотрицательные значения, если ;

4) ООФ: ;

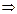
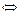
здесь ООФ учитывает ограничения операции логарифмирования (логарифмы существуют только от положительных чисел) и операции деления (на ноль делить нельзя);

ОЗФ определяется после построения графика функции;

5) , ООФ: ;

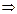
здесь ООФ записана по смыслу задания функции;

ОЗФ: – определена по графику функции ;

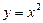
6) последовательность с общим членом может рассматриваться как функция натурального аргумента n, то есть ООФ: ;

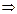
здесь ООФ записана по смыслу задания функции; ОЗФ: ;

7) ООФ: ; ОЗФ: .

Таким образом, в качестве ООФ и ОЗФ могут получиться любые множества: непрерывные или дискретные, бесконечные или конечные, в том числе может получиться пустое множество.

Дата добавления: 2015-10-19 ; просмотров: 13877 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Область допустимых значений: теория и практика

Конкурс исследовательских и проектных работ учащихся

«ИНТЕЛЛЕКТУАЛЬНОЕ БУДУЩЕЕ МОРДОВИИ»

ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ:

Автор: Малышева Оксана

2. Исторический очерк 4

3. «Место» ОДЗ при решении уравнений и неравенств 5-6

4. Особенности и опасность ОДЗ 7

5. ОДЗ – есть решение 8-9

6. Нахождение ОДЗ – лишняя работа.

Равносильность переходов 10-13

Уравнения и неравенства, в которых нужно находить область допустимых значений, не нашли места в курсе алгебры систематического изложения, возможно поэтому мои сверстники часто делают ошибки при решении таких примеров, уделив много времени их решению, забыв при этом об области допустимых значений. Это и определило проблему данной работы.

В настоящей работе предполагается исследовать явление существования области допустимых значений при решении уравнений и неравенств разных типов; проанализировать данную ситуацию, сделать логически корректные выводы в примерах, где нужно учитывать область допустимых значений.

Опираясь на имеющийся опыт и теоретическую базу, собрать основные сведения об области допустимых значений и её использовании в школьной практике; Проанализировать решения разнообразных типов уравнений и неравенств (дробно-рациональных, иррациональных, логарифмических, содержащих обратные тригонометрические функции); Проверить ранее полученные при решении различных уравнений и неравенств результаты, убедиться в надёжности способов и методов их решения; Определить «место» области допустимых значений при решении уравнений и неравенств; Применить полученные материалы исследования в ситуации, которая отличается от стандартной, и использовать их при подготовке к ЕГЭ.

При решении этих задач использованы следующие методы исследования: анализ, статистический анализ, дедукция, классификация, прогнозирование.

Исследование начато с повторения известных функций, изучаемых в школьной программе. Область определения многих из них имеет ограничения.

Область допустимых значений встречается при решении: дробно-рациональных уравнений и неравенств; иррациональных уравнений и неравенств; логарифмических уравнений и неравенств; уравнений и неравенств, содержащих обратные тригонометрические функции.

Прорешав множество примеров из различных источников (пособий по ЕГЭ, учебников, справочников), выделили решение примеров по следующим принципам:

· можно решить пример и учесть ОДЗ (самый распространённый способ)

· можно решить пример, не учитывая ОДЗ

· можно только учитывая ОДЗ прийти к правильному решению.

Изучен анализ результатов ЕГЭ за прошедшие годы. Много ошибок было допущено в примерах, в которых нужно учитывать ОДЗ. Практическое значение работы заключается в том, что ее содержание, оценки и выводы могут быть использованы в преподавании математики в школе, при подготовке к итоговой аттестации школьников 9 и 11 классов.

2. Исторический очерк

Как и остальные понятия математики, понятие функции сложилось не сразу, а прошло долгий путь развития. В работе П. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. 1679) говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И. Барроу («Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием функции. В геометрическом и механическом виде это понятие мы находим и у И. Ньютона. Однако термин «функция» впервые появляется лишь в 1692 у Г. Лейбница и притом не совсем в современном его понимании. Г. Лейбниц называет функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.

Первое определение функции в смысле, близком к современному, встречается у И. Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Л. Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». Впрочем, уже Л. Эйлеру не чуждо и современное понимание функции, которое не связывает понятие функции с каким-либо аналитическим её выражением. В его «Дифференциальном исчислении» (1755) говорится: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функциями вторых».

С начала XIX века уже всё чаще и чаще определяют понятие функции без упоминания об её аналитическом изображении. В «Трактате по дифференциальному и интегральному исчислению» (1797—1802) С. Лакруа говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних». В «Аналитической теории тепла» Ж. Фурье (1822) имеется фраза: «Функция f(x) обозначает функцию совершенно произвольную, то есть последовательность данных значений, подчинённых или нет общему закону и соответствующих всем значениям x, содержащимся между 0 и какой-либо величиной x». Близко к современному и определение Н. И. Лобачевского: «…Общее понятие функции требует, чтобы функцией от x называть число, которое даётся для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подаёт средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной». Там же немного ниже сказано: «Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи понимать как бы данными вместе». Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое П. Дирихле (1837), неоднократно предлагалось и до него:

у есть функция переменной х (на отрезке ), если каждому значению х (на этом отрезке) соответствует совершенно определённое значение у, причем безразлично, каким образом установлено это соответствие — аналитической формулой, графиком, таблицей, либо даже просто словами. [[1]]

3. «Место» области допустимых значений при решении уравнений и неравенств

При решении уравнений и неравенств часто возникает дилемма: находить область допустимых значений или нет, выбрать традиционный способ решения или воспользоваться нерациональным, объёмным, чтобы рассмотреть все варианты, не совершить ошибку и прийти, наконец, к верному решению.

Для начала вспомним методы решения уравнений и неравенств разных видов и уровней сложности, рассмотрим частные случаи.

1. При решении дробно-рациональных уравнений и неравенств знаменатель не должен равняться нулю.

2. Решение иррациональных уравнений и неравенств.

2.1. Простейшие иррациональные уравнения имеют вид . Возведя обе части уравнения в квадрат, мы избавимся от иррациональности. Но обратим внимание на то, что возведение в квадрат, вообще говоря, не равносильное преобразование, и при возведении в квадрат мы можем получить лишние корни. Если корни получились целые, то несложно произвести проверку. Но в некоторых случаях производить проверку неудобно. Тогда используют сведение данного уравнения к равносильной системе:

В данном случае нет необходимости находить ОДЗ: из первого уравнения следует, что при полученных значения х выполняется неравенство: .

2.2. Решением уравнения вида является система:

Поскольку в уравнение и входят равноправно, то вместо неравенства , можно включить неравенство , и естественно, надо выбирать из них наиболее простое.

2.3. Схемы решения основных иррациональных неравенств:

3. Решение логарифмических уравнений и неравенств.

3.1. Схема решения логарифмического уравнения

Но проверить достаточно только одно условие ОДЗ.

3.2. Схема решения логарифмического неравенства вида : 1) 2)

4. Тригонометрические уравнения вида равносильны системе (вместо неравенства в систему можно включить неравенство ).

Уравнения равносильны уравнению

4. Особенности и опасность области допустимых значений

Рассмотрим, к примеру, такое неравенство:

Здесь ищется ОДЗ, и неравенство решается. Однако при решении этого неравенства школьники иногда считают, что вполне можно обойтись без поиска ОДЗ, точнее, можно обойтись и без условия

В самом деле, для получения верного ответа необходимо учесть и неравенство , и .

А вот, например, решение уравнения:

Решают его, естественно, избавляясь от логарифмов, но затем найденные значения нередко проверяются на выполнение системы трех таких неравенств:

5. Область допустимых значений – есть решение

И наконец, в массе примеров нахождение ОДЗ позволяет получить ответ без громоздких выкладок, а то и вовсе устно.

1. ОД3 представляет собой пустое множество, а значит, исходный пример не имеет решений.

1) 2) 3)

2. В ОДЗ находится одно или несколько чисел, и несложная подстановка быстро определяет корни.

1) , х=3

2) Здесь в ОДЗ находится только число 1, и после подстановки видно, что оно не является корнем.

3) В ОДЗ находятся два числа: 2 и 3, и оба подходят.

4) > В ОДЗ находятся два числа 0 и 1, и подходит только 1.

Эффективно может использоваться ОДЗ в сочетании с анализом самого выражения.

5) , а значит, . Решая последнее неравенство, получим х 2. При этом . Значит, исходное равенство невозможно и решений нет.

А теперь приведём пример, который был предложен учителем на уроке алгебры. Решить его сразу нам не удалось, но когда мы нашли ОДЗ, всё стало ясно.

Найдите целочисленный корень уравнения Найдём ОДЗ:

Целочисленное решение возможно лишь при х=3 и х=5. Проверкой находим, что корень х=3 не подходит, а значит ответ: х=5.

6. Нахождение области допустимых значений – лишняя работа. Равносильность переходов.

Можно привести примеры, где ситуация ясна и без нахождения ОДЗ.

Равенство невозможно, ибо при вычитании из меньшего выражения большее должно получатся отрицательное число.

2. .

Сумма двух неотрицательных функций не может быть отрицательной.

Приведу также примеры, где нахождение ОДЗ затруднено, а иногда просто невозможно.

И, наконец, поиски ОДЗ являются очень часто просто лишней работой, без которой прекрасно можно обойтись, доказав тем самым понимание происходящего. Тут можно привести громадное число примеров, поэтому выберем только наиболее типичные. Главным приемом решения являются в этом случае равносильные преобразования при переходе от одного уравнения (неравенства, системы) к другому.

1.. ОДЗ не нужна, ибо, найдя те значения х, при которых х2=1, мы не можем получить х=0.

2. . ОДЗ не нужна, ибо мы выясняем, когда выполняется равенство подкоренного выражения положительному числу.

3. . ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.

ОДЗ не нужна, ибо подкоренное выражение равно квадрату некоторой функции, а потому не может быть отрицательным.

5. ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.

6. . ОДЗ не нужна, так как выражение всегда положительно.

7. Для решения достаточно только одного ограничения для подкоренного выражения. В самом деле, из записанной смешанной системы следует, что и другое подкоренное выражение неотрицательно.

8. ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.

9. ОДЗ не нужна, так как достаточно, чтобы были положительны два из трех выражений под знаками логарифма, чтобы обеспечить положительность третьего.

10. ОДЗ не нужна, так как положительность трёхчлена следует из условий системы неравенств.

11. ОДЗ не нужна по тем же соображениям, что и в предыдущем примере.

Стоит, однако, заметить, что при решении способом равносильных преобразований помогает знание ОДЗ (и свойств функций).

Вот несколько примеров.

1. . ОД3 , откуда следует положительность выражения в правой части, и возможно записать уравнение, равносильное данному, в таком виде . Полученный результат надо проверить по ОДЗ.

2. ОДЗ: . Но тогда , и при решении этого неравенства не надо рассматривать случай, когда правая часть меньше 0.

3. . Из ОДЗ следует, что , а потому случай, когда , исключается.

В целом эффективность способа равносильных преобразований вроде бы ясна. С их помощью мы добираемся до ответа и без поисков ОДЗ. Значит ли это, что имеется некий универсальный способ и осталось только научиться им пользоваться? Но это не совсем так. Тому несколько причин. Теорем о равносильных преобразованиях довольно много, они непросты для запоминания, и уверенное владение ими – дело не простое. Часто, пользуясь равносильными преобразованиями, начинаешь ставить этот знак при любых переходах от одного уравнения к другому, как действительно равносильных, так и не являющихся таковыми. Теоремы же эти быстро забываются.

1. Переход в общем виде выглядит так:

В данном примере выражение под знаком логарифма, стоящего справа, всегда положительно. Поэтому применительно к этому примеру та часть условий равносильности, которая записана в виде совокупности, ничего не добавляет. Но дав такое решение, можно просто забыть об этой совокупности.