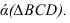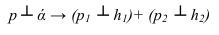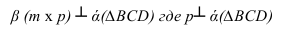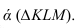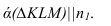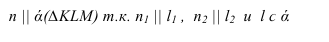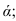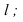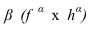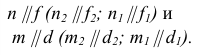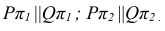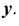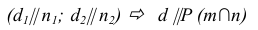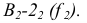Чем определяется взаимная параллельность прямой и плоскости

Лекция «Параллельность прямой и плоскости»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Параллельность прямой и плоскости.

Возможны три расположения прямой и плоскости:

1. прямая лежит в плоскости

1. прямая и плоскость имеют только одну общую точку, т.е. пересекаются

1. прямая и плоскость не имеют ни одной общей точки

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Существует еще два утверждения, которые используются при решении задач:

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.

Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

MC

Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

. BC=AD= 8 см;

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Лекция «Параллельность прямых в пространстве»

Презентация на тему «Решение задач по нахождению угла между прямой и плоскостью»

Презентация на тему «Решение задач на нахождение угола между прямыми в пространстве»

Внеклассное мероприятие по геометрии «Великие математики»

Тексты задач по окружности из сборника по подготовке к ОГЭ

Презентация урока подготовки к ОГЭ задача по теме «Окружность» 9 класс

Билеты для зачета по геометрии 8 класс

Презентация по геометрии на тему «Площади четырехугольников»(8 класс)

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5388709 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В Петербурге школьникам разрешили уйти на каникулы с 25 декабря

Время чтения: 2 минуты

Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Взаимное положение прямой и плоскости с примерами

Содержание:

Проекции прямого угла:

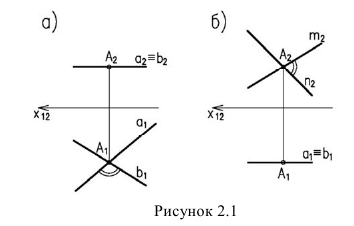
Величина угла между двумя пересекающимися прямыми в общем случае на проекциях искажается. В натуральную величину этот угол будет проецироваться в том случае, если плоскость угла параллельна одной из плоскостей проекций. Тогда другие проекции сторон угла совпадают и параллельны оси проекций (рисунок 2.1).

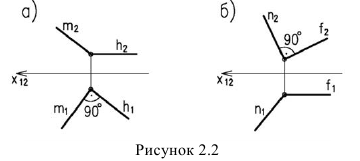
Прямой угол проецируется в натуральную величину, если одна из его сторон параллельна одной из плоскостей проекций (рисунок 2.2).

Взаимное положение примой и плоскости, двух плоскостей

Прямая относительно плоскости может занимать следующие положения: лежать в плоскости (что рассматривалось ранее); быть ей параллельна; пересекать плоскость; быть перпендикулярной плоскости (т.е. пересекать под прямым углом).

Две плоскости могут быть:

Перпендикулярность примой и плоскости

Условие перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости.

Так как прямой угол между прямыми линиями проецируется на плоскость проекций без искажения, если одна из прямых параллельна этой плоскости проекций, то пересекающимися прямыми плоскости, которые нужно взять для построения перпендикуляра, могут быть только ее горизонталь и фронталь.

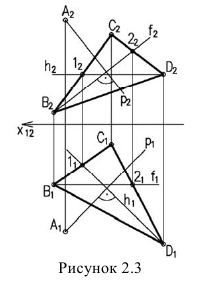
Следовательно, прямая перпендикулярна плоскости, если ее фронтальная проекция перпендикулярна фронтальной проекции фронгали плоскости, а горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости.

На рисунке 2.3 через точку 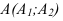проведена прямая, перпендикулярная плоскости

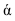
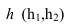
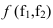
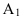
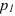
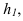
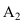
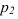
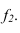
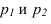
В плоскости проведены горизонталь и фронталь, затем через проведена горизонтальная проекция перпендикуляра под прямым углом к а через точку фронтальная проекция перпендикуляра иод прямым углом к Прямые есть проекции искомого перпендикуляра р.

Перпендикулярности двух плоскостей

Две плоскости взаимно перпендикулярны, если одна из них содержи! перпендикуляр к другой.

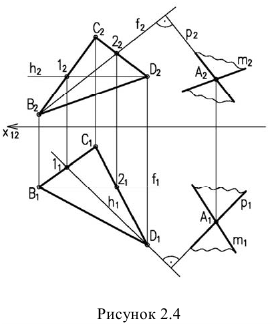
Пусть через данную прямую т необходимо провести плоскость, перпендикулярную плоскости а. заданной треугольником 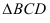(рисунок 2.4).

Для решения задачи достаточно на прямой т взять произвольную точку А и провести через нее прямую р, перпендикулярную данной плоскости .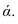

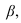
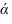
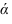
Пересекающиеся прямые m и р образуют плоскость которая содержит прямую р, перпендикулярную плоскости следовательно, плоскости (i и взаимно перпендикулярны.

Параллельность прямой и плоскости

Условие параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости.

Рассмотрим пример решения задачи на параллельности прямой и плоскости.

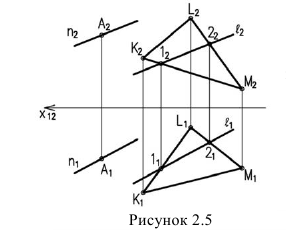
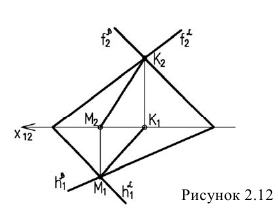
Задача: построить фронтальную проекцию прямой n, проходящей через точку А и параллельной

Для решения задачи:

Проводим горизонтальную проекцию прямой 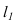в плоскости

Строим фронтальную проекцию

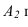
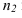
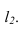
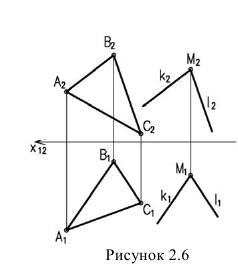
Через точку проводим параллельную Таким образом получим:

Параллельность двух плоскостей

Условие параллельности двух плоскостей:

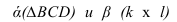
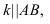
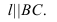
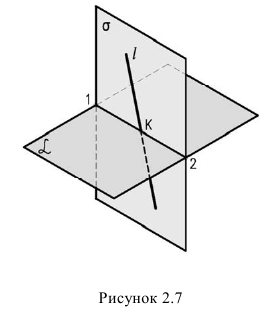
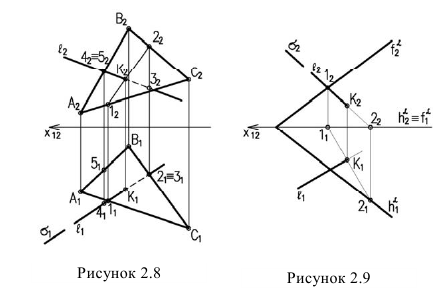
Изображенные на рисунке 2.6 плоскости взаимнопараллельныe, т.к. Пересечение прямой и плоскости

Задача на нахождение точки пересечения прямой линии с плоскостью является первой основной позиционной задачей курса начертательной геометрии.

Алгоритм решения задачи (рисунок 2.7):

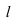
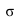
1. Прямую заключаем во вспомогательную плоскость (удобнее всего в проецирующую);

2. Находим линию пересечения (1-2) вспомогательной плоскости с заданной

3. Отмечаем точку пересечения К найденной линии пересечения (1-2) с заданной прямой

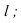
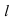
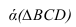
4. Определяем видимость прямой На основании данного алгоритма определим точку пересечения прямой с плоскостью (рисунок 2.8) и с плоскостью

Пересечение двух плоскостей

Две плоскости пересекаются по прямой линии, поэтому для её построения достаточно найти две точки одновременно принадлежащие двум плоскостям.

Рассмотрим несколько случаев построения линии пересечения двух плоскостей.

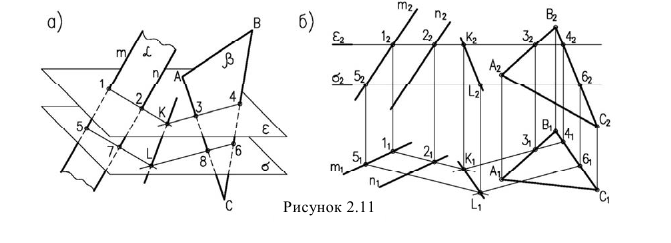
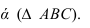
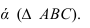
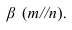
Задача сводится к нахождению точек пересечения прямых m и n с плоскостью а. Соединив точки пересечения К и М получим линию пересечения плоскости с плоскостью Видимость определяется по конкурирующим точкам.

Алгоритм решения задачи (рисунок 2.11):

Видимость при этом не определяется.

В данном случае в качестве плоскостей-посредников могут быть использованы плоскость проекций.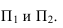

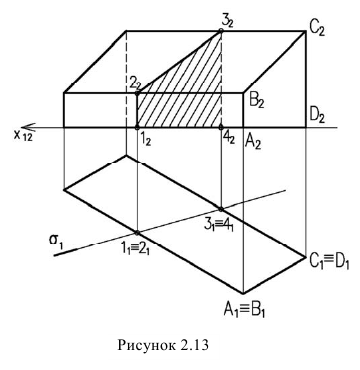
Пересечение многогранника проецирующей плоскостью

Так как секущая плоскость горизонтально-проецирующая, то фронтальную проекцию сечения можно построить, определив точку пересечения каждого ребра с плоскостью о (рисунок 2.13)

Взаимное положение двух плоскостей

Две плоскости могут принадлежать одна другой; быть параллельны или пересекаться.

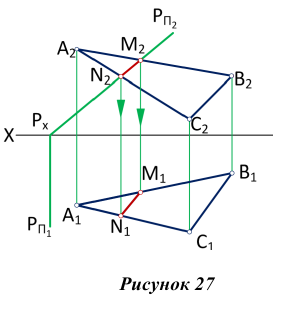
Пересечение плоскости общего положения с плоскостью частного положения

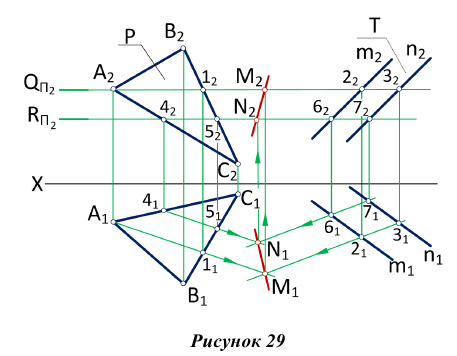
На рис. 27 показано построение линии пересечения фронтально-проецирующей плоскости Р с плоскостью треугольника AВС.
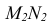
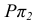
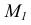
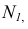
Так как линия пересечения двух плоскостей принадлежит фронтально-проецирующей плоскости Р, то ее фронтальная проекция совпадает с фронтальным следом плоскости Р. Горизонтальная проекция искомой линии пройдет через точки и расположенные на горизонтальных проекциях AВ и АС соответствующих сторон треугольника (рис. 27).

Пересечение двух плоскостей общего положения

Задача. Построить линию пересечения двух плоскостей общего положения

Алгоритм решения задачи (рис. 28)

Плоскости параллельны

Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

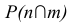
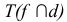
Изображенные на рис. 31 плоскости и параллельны, т.к.

Плоскости общего положения также параллельны, если два любых одноименных следа параллельны между собой.

Изображенные на рис. 32 плоскости Р и Q параллельны, т.к.

Взаимное положение прямой линии и плоскости

Прямая может лежать в плоскости, пересекать плоскость и быть параллельной плоскости.

Пересечение прямой линии с плоскостью частного положения

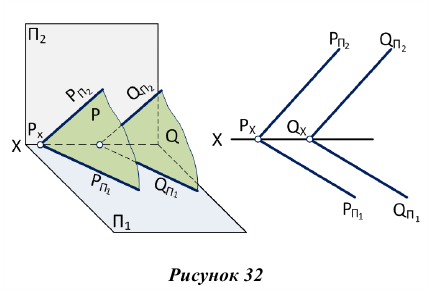
Если заданная плоскость перпендикулярна к какой-либо плоскости проекций (рис.33, а), то она проецируется на эту плоскость проекций в виде прямой линии, на которой обязательно будут находиться соответствующие проекции всех точек, принадлежащих данной плоскости, в том числе и проекции точки пересечения какой-то прямой с заданной плоскостью (точка встречи прямой с плоскостью). Поэтому точка встречи прямой с плоскостью частного положения находится па эпюре без дополнительных построений (рис. 33,6).

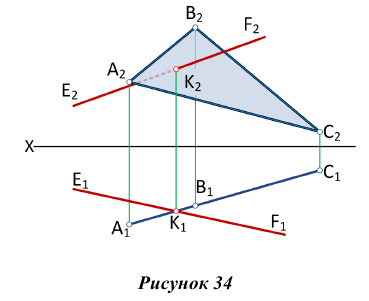
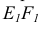
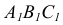
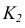
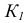
На рис. 34 точка встречи прямой EF с горизонтально-проецирующей плоскостью, заданной треугольником ABC, является точкой пересечения горизонтальных проекций и прямой и треугольника. Фронтальная проекция точки пересечения лежит на линии проекционной связи, проведенной из точки до пересечения с фронтальной проекций прямой EF. Принято считать, что всякая плоскость (в том числе и плоскость проекций) непрозрачна. Поэтому часть прямой, которая находится за плоскостью, является невидимой и показана на эпюрах (рис. 33,6; 34) штриховой линией.

Определение видимости на эпюрах

Вопрос о видимости линий или поверхностей всегда может быть сведен к вопросу о видимости точек. Если несколько точек находятся на общей для них линии связи, то видимой будет только одна из них — наиболее удаленная от той плоскости проекций, по отношению к которой определяется видимость.

Точки, расположенные на одной линии связи, называются конкурирующими. Точки А, В и С, D — конкурирующие (рис. 35).

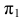
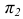
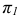
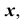
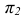
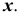
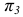
Относительно плоскости проекций видимой будет точка А; относительно плоскости проекций видимой будет точка D, т. е. относительно плоскости видимой будет та точка, фронтальная проекция которой находится дальше от оси а относительно плоскости видимой будет та точка, горизонтальная проекция которой находится дальше от оси Аналогично: относительно плоскости видимой будет та точка, горизонтальная проекция которой будет находиться дальше от оси

Пересечение прямой линии с плоскостью общего положения

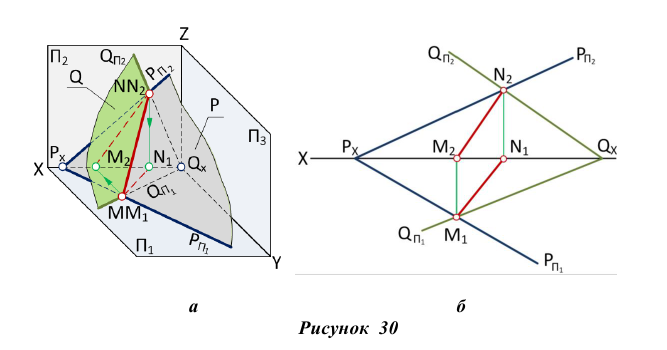
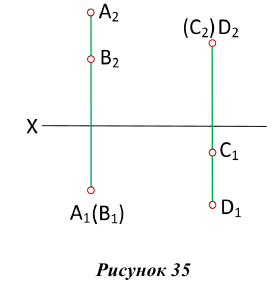
Точку пересечения прямой линии АВ с плоскостью общего положения Р (рис. 36) находят следующим образом:

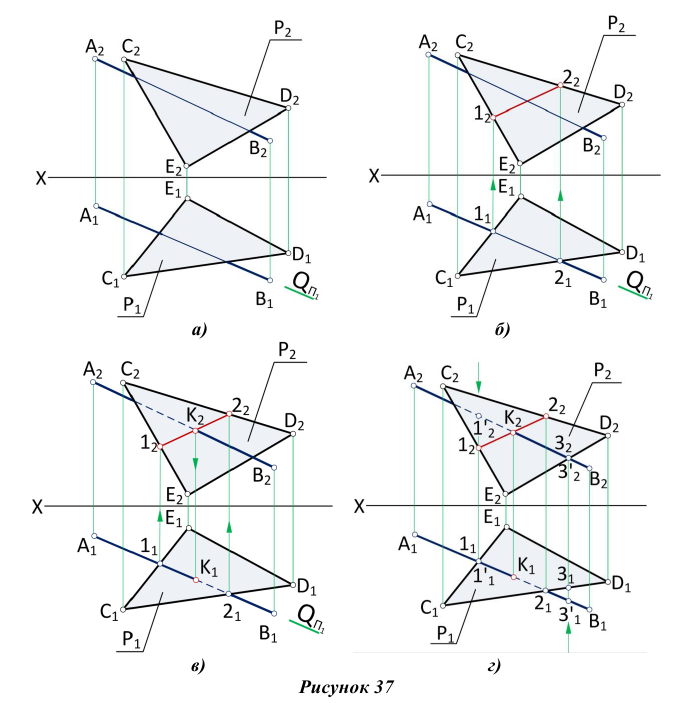
Пошаговые построения по определению точки пересечения прямой АВ с плоскостью треугольника CDE на эпюре приведены на рис. 37 (а-в).

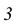
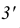
Аналогично, используя конкурирующие точки и определяем видимость прямой АВ и плоскости по отношению к фронтальной плоскости проекций.

Задачи, на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение прямой с плоскостью.

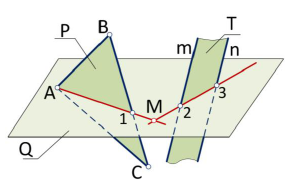
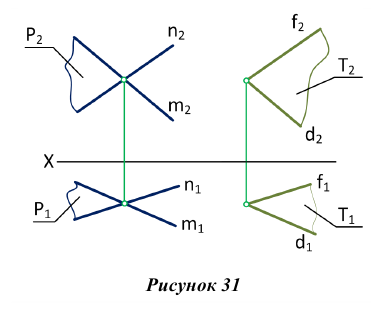
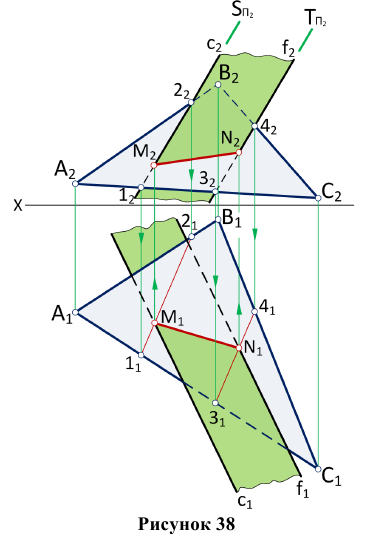
Одна из изображенных на рис. 38 плоскостей задана треугольником AВС, а вторая — двумя параллельными прямыми с и f.

Точка N найдена аналогично. Прямая MN — искомая. Видимость на рис. 86 определена из условия, что заданные плоскости ограничены треугольником и двумя параллельными прямыми, определяющими их.

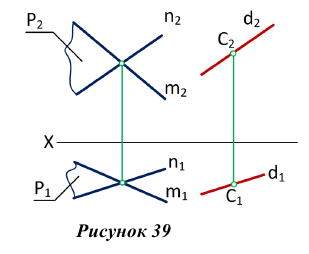
Прямая параллельна плоскости

На рис. 39 через точку С проведена прямая d, параллельная плоскости Р, заданной пересекающимися прямыми т и п.

Прямая d параллельна прямой n, принадлежащей плоскости 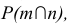следовательно, прямая d параллельна этой плоскости:

Прямая перпендикулярна плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

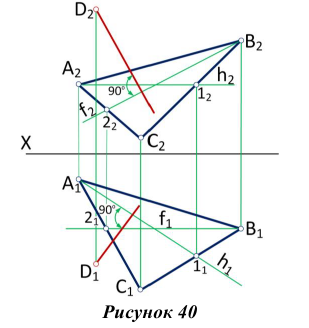
Чтобы построить перпендикуляр из точки D на плоскость треугольника AВС (рис.40) необходимо предварительно построить
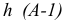
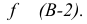
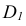
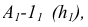
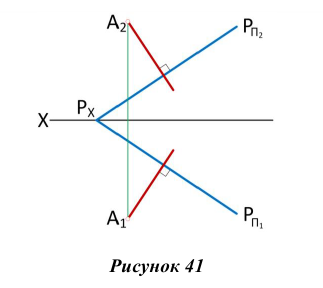
горизонталь и фронталь плоскости Горизонтальная проекция перпендикуляра пройдет через точку перпендикулярно к горизонтальной проекции горизонтали а фронтальная проекция — перпендикулярно к фронтальной проекции фронтали

Если же плоскость задана следами, то, учитывая, что фронтальная проекция любой фронтали в этой плоскости всегда параллельна фронтальному следу плоскости, а горизонтальная проекция любой горизонтали параллельна горизонтальному следу плоскости, легко видеть (рис. 41), что проекции перпендикуляра к плоскости должны быть перпендикулярны соответствующим следам плоскости.

Плоскости перпендикулярны

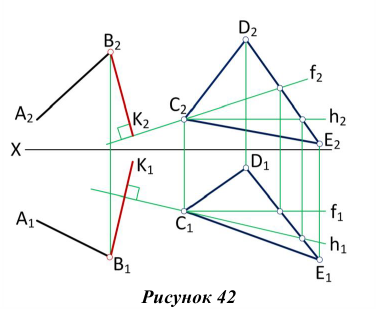
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. На рис. 42 через прямую АВ проведена плоскость, перпендикулярная плоскости треугольника CDE. Для этого из точки В прямой АВ восстановлен перпендикуляр ВК к плоскости треугольника 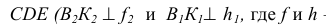— фронталь и горизонталь плоскости треугольника CDЕ ). Плоскость, определяемая пересекающимися прямыми АВ и ВК— искомая.

Если возникает необходимость в построении взаимно перпендикулярных прямых общего положения, необходимо построить плоскость, перпендикулярную заданной прямой, и взять в ней любую прямую.

Задача.

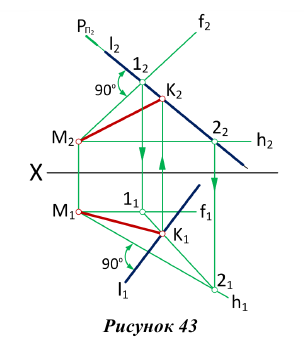
Через точку М провести прямую, перпендикулярную прямой

Для построения взаимно перпендикулярных прямых (рис. 43), одна из которых 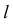задана, а вторая (чтобы задача имела единственное решение) должна проходить через какую-либо определенную точку М, надо выполнить следующее:

Задача:

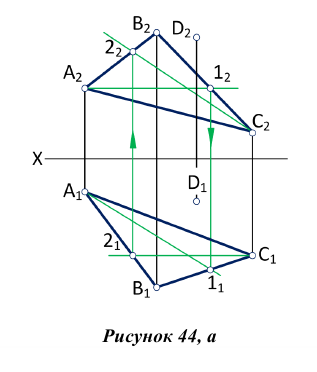
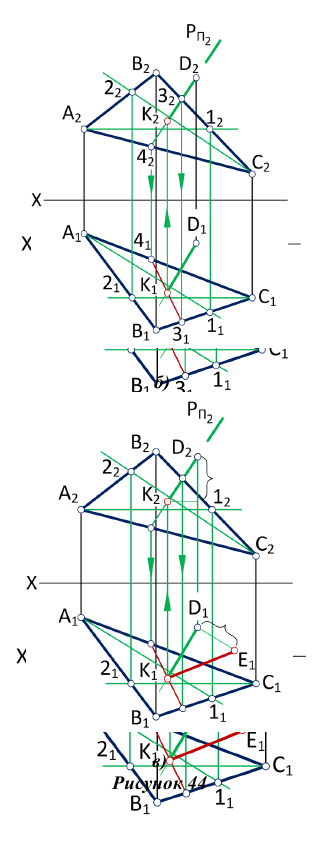
Определить расстояние от точки до плоскости, заданной треугольником ABC (рис.44)

Расстояние от точки до плоскости определяется длиной перпендикуляра, опущенного из точки на плоскость. Поэтому решение этой задачи выполняем в следующей последовательности:

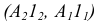
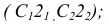
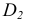
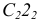
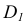
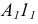
1. Из точки D опускаем перпендикуляр на плоскость треугольника AВС (рис.44, а), для этого в плоскости треугольника проводим горизонталь и фронталь затем из точки опускаем перпендикуляр на — получаем фронтальную проекцию перпендикуляра; а из точки -на — получаем горизонтальную проекцию перпендикуляра к плоскости

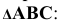
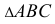
2. Находим точку пересечения перпендикуляра с плоскостью заключаем перпендикуляр во вспомогательную секущую плоскость Р; строим линию пересечения плоскости с плоскостью Р; определяем искомую точку К в пересечении перпендикуляра и построенной линии пересечения 3-4 (рис. 44,6).

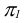
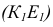
3. Методом прямоугольного треугольника определяем натуральную величину отрезка DK, для чего в плоскости (рис. 44,в) строим прямоугольный треугольник один катет которого является горизонтальной проекций перпендикуляра, а второй равен разности высот точек D и К. Гипотенуза построенного треугольника определяет искомое расстояние от точки D до плоскости треугольника ABC.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник