Чем определяется выбор системы координат
Большая Энциклопедия Нефти и Газа
Выбор системы координат определяется формой ограничивающих рабочих поверхностей машин или аппаратов, в которых деформируется жидкость. Форма записи уравнений в различных системах координат в общем виде приведена в специальной литературе. [1]
Выбор системы координат зависит от условий перекачивания газа и целей расчета. Графики строят по результатам испытания компрессора на газе определенного состава. При отсутствии опытных данных используют теоретические формулы. [2]
Выбор системы координат определяется, с одной стороны, характером движения точки ( прямолинейное движение, движение на плоскости, движение в пространстве), с другой стороны, видом действующих на точку сил. Так, например, при прямолинейном движении точки естественно выбрать за ось координат прямую, по которой движется точка. [3]
Выбор системы координат для записи векторного равенства в виде системы скалярных равенств определяется соображениями удобства этой системы для рассматриваемой конкретной физической задачи, но само векторное равенство, естественно, от такого выбора никак не зависит. В этом и состоит преимущество использования векторных величин для записи физических закономерностей. [4]
Выбор системы координат зависит от условий перекачивания газа и целей расчета. Графики строят по результатам испытания компрессора на газе определенного состава. При отсутствии опытных данных используют теоретические формулы. [5]
Выбор системы координат зависит от вида симметрии, присущей конкретной задаче. Так, в случае зеркальной симметрии применима декартова система координат, в то время как аксиально-симметричной задаче более адекватна цилиндрическая система координат. Очень важен правильный выбор системы координат, поскольку это позволяет свести трехмерную задачу к двухмерной или даже одномерной задаче. В самом деле, аксиальная симметрия означает, что поля не зависят от азимутального угла а. В таком случае распределение полей во всем пространстве может быть представлено их распределением в любой плоскости, отвечающей фиксированному углу а. Если система обладает сферической симметрией, то ситуация упрощается в еще большей степени. [7]
Выбор системы координат в первую чередь зависит от того, в какой системе координат задано расположение отверстий на чертеже. Естественно, если отверстия, подлежащие растачиванию, заданы в полярной системе координат и они находятся в одной плоскости, целесообразно растачивание производить на горизонтальном поворотном столе. [9]
Выбор системы координат зависит от взаимного расположения обрабатываемых поверхностей и их положения относительно базовых поверхностей. [10]
Выбор системы координат ( полярные, прямоугольные или косоугольные) в основном определяется конструкцией балансируемой детали. При свободе выбора координат полярные координаты предпочтительней, так как при этом уравновешивание достигается съемом меньших количеств материала, измерительное устройство получается проще и значительно упрощается позиция исправления неуравновешенности. Для исправления неуравновешенности в прямоугольных координатах требуется либо восемь механизмов, задающих глубину сверления, либо четыре механизма, задающих глубину сверления, и два механизма, определяющих квадранты, в которых находится вектор неуравновешенности. Если задача исправления неуравновешенности решается в полярных координатах, то требуется четыре механизма: два механизма, задающих глубину сверления, и два механизма, задающих угол, под которым направлен вектор неуравновешенности. [11]
Выбор системы координат зависит от размеров исследуемых участков поверхности, как следствие, от влияния кривизны Земли. При изображении небольших участков Земли часть уровненной поверхности можно принять за плоскость. [12]
Выбор локалъно-геодезяческой системы координат означает поэтому обращение в нуль в данной точке всех первых производных от компонент метрического тензора. [13]
Такой выбор системы координат позволяет задачу решить сразу же, не прибегая к делению ее на две части: движение тела вверх и движение вниз что обычно делают учащиеся при решении задач подобного рода. [15]
Система координат
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.
В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.
Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Содержание
Список наиболее распространённых систем координат
Основные системы
В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.
Декартовы координаты
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел 
:
В пространстве же необходимо уже 3 координаты 
:
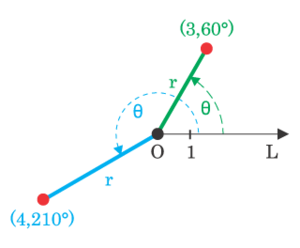
Полярные координаты
В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.
Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.
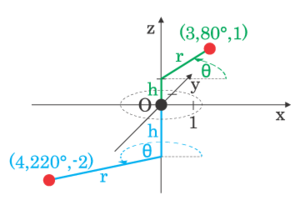
Цилиндрические координаты
Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем 
. В терминах декартовой системы координат,
Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение 
, тогда как в цилиндрических оно выглядит как r = c
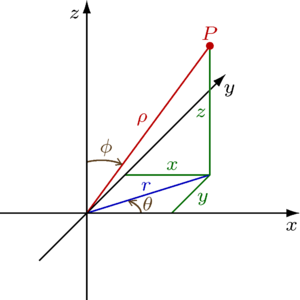
Сферические координаты
Сферические координаты — трехмерный аналог полярных
Обозначения, принятые в Америке
В сферической системе координат, расположение точки P определяется тремя компонентами: 
. В терминах декартовой системы координат,
Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.
Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.
Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как 
, тогда как в сферических становится намного проще: 
.
Европейские обозначения
В Европе принято использовать другие обозначения. Положение точки задаётся числами: 
, Где r — расстояние от точки до начала координат, 
— полярный угол, который изменяется в пределах от 0 до π, 
— Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.
Переход из одной системы координат в другую
Декартовы и полярные
GIS-LAB
Географические информационные системы и дистанционное зондирование
Введение в геоинформационные системы
Системы координат и проекции
Теоретическая часть
Объекты на карте связаны с реальными объектами на местности с помощью пространственных координат. Местоположение объектов на поверхности земли определяется при помощи географических координат. Хотя географические координаты хорошо подходят для определения местоположения объекта, они не годятся для определения его пространственных характеристик, таких как длина, площадь и т.д., так как географические широта и долгота не являются однозначными единицами измерения. Градус широты равен градусу долготы только на экваторе. Для преодоления этих трудностей, данные переводят из сферических географических координат, в прямоугольные спроектированные координаты.
Географическая и спроектированная системы координат
Таким образом, существует 2 типа систем координат: географические системы координат и спроектированные системы координат.
Такое представление иногда называют географической проекцией.
Локальная система координат
Распространенные географические системы координат.
Проекция
Виды проекций
По типу поверхности на которую осуществляется проектирование проекции разделяются на:
Конические (проектирование сфероида на коническую поверхность)
Цилиндрические (проектирование сфероида на цилиндрическую поверхность)
Азимутальные (проектирование сфероида на плоскость касательную сфероида)
Распространенные проекции
Достаточно широко распространены в России и мире группы проекций UTM (Universal Transverse Mercator) и ГК (Гаусса-Крюгера, больше распространена в России и странах Восточной Европы). Обе этих группы базируются на одной поперечной проекции Меркатора (Transverse Mercator), однако имеют различную номенклатуру (нумерацию зон) и параметры проекций для каждой зоны.
Переход между системами координат
Файл описания проекции
Проекция данных записывается в специальный файл (имеющий расширение prj), в котором указывается система координат, проекция, единицы измерения и другие данные, важные для пространственной привязки данных. Без этого файла, определение проекции данных может быть затруднительно. Этот файл помогает ГИС определить пространственную привязку данных и перевести их в другую проекцию, если такая команда будет дана ГИС.
Подробнее о проекциях и системах координат:
Часто задаваемые вопросы по координатам, проекциям, системам координат >>>
Практическая часть
В практической части этой главы Вы научитесь:
Упражнение 1. Назначение спроектированной системы координат фрейму данных
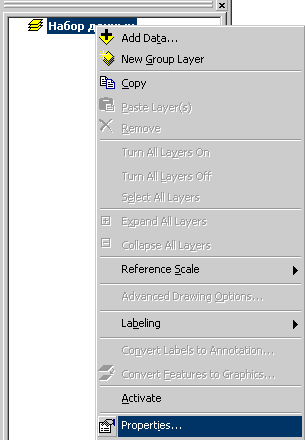
— нажатием правой кнопкой мыши на названии набора данных в таблице содержания вида
— или выбором в главном меню в закладке View\Data Frame Properties.
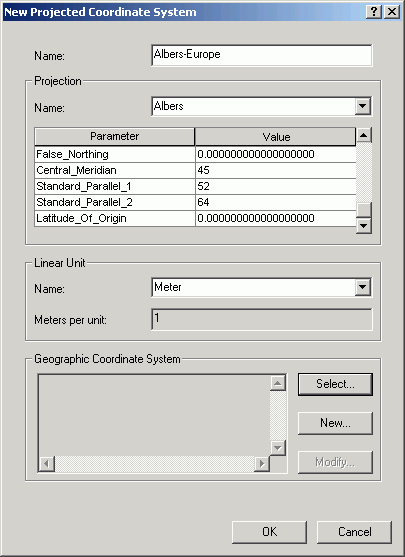
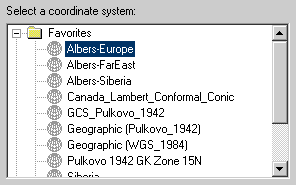
Кроме задания парметров проекции необходимо указать используемую географическую систему координат. Для этого нажмите кнопку Select и из папки Europe выберите систему координат Pulkovo 1942.prj
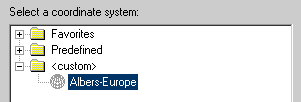
Как Вы увидите, вновь созданная проекция добавилась в папку
Часто бывает так, что заданные вручную параметры проекции необходимо будет использовать многократно. Для того, чтобы не прописывать эти параметры каждый раз заново, Вы можете сохранить свою проекцию в папку Favorites. Для этого необходимо нажать кнопку Add To Favorites
Теперь для того, чтобы задать эту проекцию фрейму данных его нужно будет просто выбрать из списка в папке Favorites и нажать Apply.
Подробнее о добавлении проекций в ArcGIS >>>
Упражнение 2. Смена географической системы координат
Данный пример иллюстрирует особенности работы в ArcGIS с данными, находящимися в разных системах координат и особенности «поведения» ПО, необходимые при этом учитывать.
Упражнение 3. Экспорт данных в другой системе координат (перепроектировка)
Данное упражнение иллюстрирует один из способов перевода данных из одной системы координат в другую, так чтобы новая система координат была закреплена за данными постоянно, независимо от того, в какую систему координат имеет набор данных.
Системы координат в геодезии — какие бывают и как используются?
В данной статье мы разбираем основные вопросы по геодезии. Что такое системы координат, какие виды СК выделяют, какие из них используются на практике и для чего. А также, отвечаем на вопрос, почему мы предоставляем поправки в международной системе координат.
Содержание статьи:
Надеемся, этот материал поможет получить ответы на интересующие вопросы.
Что такое система координат?
Система координат (СК) — это набор математических правил, описывающих, как координаты должны быть соотнесены с точками пространства.
Иными словами, это совокупность условий, определяющих положение и перемещение точки или объекта на прямой, на плоскости, в пространстве с помощью чисел или других символов.
Совокупность чисел, определяющих положение точки, называется координатами этой точки.
Какие бывают системы координат?
Существуют разные геодезические системы координат, они используются в зависимости от масштаба, в котором необходимо произвести расчет расположения объекта на Земле.
В рамках данной статьи, разберемся, какие именно бывают системы координат и как используются на практике в геодезии.
Полярная система координат (полярные координаты)
Полярная система координат — это система координат, положение точки в которой задается расстоянием и направлением от ее начала.
Двумерная полярная система координат может быть задана на плоскости, поверхности сферы или эллипсоида.
Плоская прямоугольная (прямолинейная система координат)
Плоская прямоугольная (прямолинейная) система координат — это система координат, определяющая положение точек по отношению к взаимно перпендикулярным осям, исходящим из ее начала.
Координаты точки в данной системе координат представлены в виде плоских прямоугольных координат x и y. В геодезии — это координаты на плоскости, на которой отображена поверхность земного эллипсоида в заданной картографической проекции.
Прямоугольная пространственная система координат
Прямоугольная пространственная система координат — это система трехмерных линейных прямоугольных координат по координатным осям Х, У, Z координат, у которой оси Х и У лежат в экваториальной плоскости, ось Х направлена к начальному меридиану, ось Z направлена на север, орты образуют правую тройку векторов, а начало координат совпадает с центром земного эллипсоида.
Координаты точки в пространственной системе координат представлены в виде геодезических (эллипсоидальных) координатах или в прямоугольных пространственных координатах.
Земные и референцные системы координат
Помимо вышеупомянутых, различают земные (общеземные) и референцные системы координат. Разбираемся, чем они отличаются.
Что такое земная система координат в геодезии?
Земная система координат — это пространственная система координат, предназначенная для количественного описания положения и движения объектов, находящихся на поверхности Земли и в околоземном пространстве.
Что такое референцная система координат в геодезии?
Референцная система координат — это система координат, созданная с целью обеспечения геодезических и картографических работ на конкретной территории. К ним можно отнести местные и условные системы координат.
Что такое геодезическая система координат?
Геодезическая система координат — это система координат, которая используется для определения точного местоположения объекта на земном шаре.
За земной шар, для удобства проведения математических расчетов в инженерной геодезии, принимают шар с R=6371.11 км. Объем земного шара при этом равен объему земного эллипсоида.
Что такое геодезические координаты?
Геодезические координаты — это величины, два из которых (геодезическая широта B и геодезическая долгота L) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота H) представляет собой высоту точки над поверхностью отсчетного эллипсоида.
В земных системах координат центр координат совпадает с центром масс Земли, поэтому прямоугольные пространственные координаты называют геоцентрическими координатами.
Системы координат также подразделяют на государственные, местные, локальные и международные.
СК, используемые на практике
Практическими реализациями пространственной геоцентрической земной системы координат являются системы координат WGS-84, ПЗ-90.11 и ГСК-2011.
Система координат WGS-84
WGS-84 (World Geodetic System (Всемирная геодезическая система координат)) – это система геодезических параметров Земли 1984 года, используемая в GPS, в число которых входит система геоцентрических координат).
Система координат ПЗ-90.11
ПЗ-90.11 (общеземная геоцентрическая система координат «Параметры Земли 1990 года») — это государственная система координат, используемая в ГЛОНАСС.
ПЗ-90.11 была установлена постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования в целях геодезического обеспечения орбитальных полетов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны Российской Федерации.
Система координат ГСК-2011
ГСК-2011 (геодезическая система координат 2011 года) – это государственная система координат, установленная постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования при осуществлении геодезических и картографических работ на территории Российской Федерации.
Система координат МСК
МСК – это местная система координат субъекта Российской Федерации, установленная для целей обеспечения проведения геодезических и картографических работ при осуществлении градостроительной и кадастровой деятельности, землеустройства, недропользования и иной деятельности.
Каждый субъект имеет свою МСК с номером данного субъекта, например, местная система координат Московской области именуется МСК-50.
Архивные системы координат
Существуют архивные системы координат, которые в настоящее время не используются (не действуют).
Среди них можно выделить:
Какие бывают системы отсчета высот?
Высоты в геодезии могут быть представлены в виде геодезических, ортометрических и нормальных и высот. Высоты также могут быть представлены в условной системе высот.
Основные системы отсчета высот:
Отсчет высот в Балтийской системе высот 1977 года ведется от нуля Кронштадтского футштока, укрепленного в устое моста через обводной канал в г. Кронштадте.
Почему мы предоставляем поправки в международной системе координат?
Поскольку ГНСС работают в реализациях земной геоцентрической системы координат, таких как WGS-84 и ПЗ-90.11, то первоначально все спутниковые определения с использованием ГНСС выполняются в этих системах координат.
В ГНСС аппаратуре и программном обеспечении все результаты (координаты, скорости, ускорения) вначале приводятся в WGS-84, которые можно представить в любой другой системе координат путем математических преобразований.
Координаты в пространственных земных системах WGS-84, ПЗ-90.11 или ГСК-2011 с точностью 1 метр практически совпадают, поэтому для спутниковых определений с такой точностью не имеет значения в какой из реализаций системы координат они представлены.
Для спутниковых определений с высокой точностью мы предоставляем дифференциальные поправки, которые применяются к измеряемым величинам в процессе спутниковых определений. Дифференциальные поправки позволяют определить пространственные координаты относительно спутниковых базовых станций с заданными координатами.
Поскольку в нашей сети координаты всех станций определены в международной системе координат WGS-84, координаты определяемых вами точек также первоначально представлены в WGS-84. Но, как уже было сказано выше, они могут быть преобразованы в любую системы координат по известным параметрам преобразования.