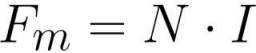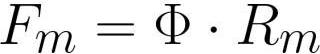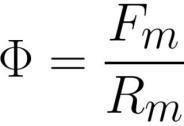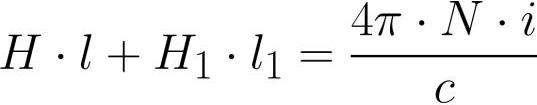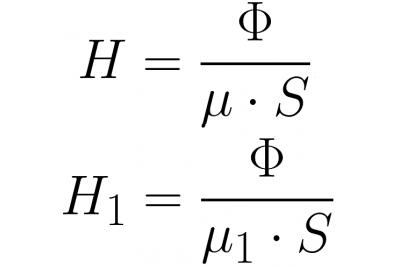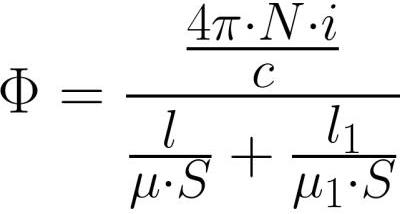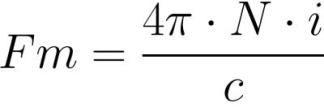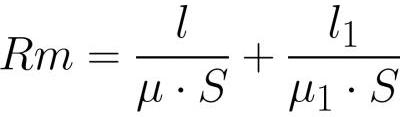Что такое магнитодвижущая сила, закон Гопкинсона

Во второй половине XIX века, английский физик Джон Гопкинсон и его брат Эдвард Гопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, получившую название «формула Гопкинсонов» или закон Гопкинсона, являющийся аналогом закона Ома (применяемого для расчета электрических цепей).

Так, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Гопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).

В результате оказалось, что магнитодвижущая сила — это физическая величина, характеризующая способность электрических токов создавать магнитные потоки. И закон Гопкинсона, в связи с этим, может успешно использоваться в расчетах магнитных цепей, так как МДС в магнитных цепях является аналогом ЭДС в электрических цепях. Датой открытия закона Гопкинсона считается 1886 год.

Величина магнитодвижущей силы (МДС) изначально измеряется в амперах, либо, если речь идет о катушке с током или об электромагните, то для удобства расчетов пользуются ее выражением в ампер-витках:

где: Fm — магнитодвижущая сила в катушке [ампер*виток], N – количество витков в катушке [виток], I – величина тока в каждом из витков катушки [ампер].

Если сюда ввести значение магнитного потока, то Закон Гопкинсона для магнитной цепи примет вид:

где: Fm — магнитодвижущая сила в катушке [ампер*виток], Ф — магнитный поток [вебер] или [генри*ампер], Rm – магнитное сопротивление проводника магнитного потока [ампер*виток/вебер] или [виток/генри].

Текстовая формулировка закона Гопкинсона изначально такова: «в неразветвленной магнитной цепи магнитный поток прямо пропорционален магнитодвижущей силе и обратно пропорционален полному магнитному сопротивлению». То есть данный закон определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в цепи:

здесь: Ф — магнитный поток [вебер] или [генри*ампер], Fm — магнитодвижущая сила в катушке [ампер*виток], Rm – магнитное сопротивление проводника магнитного потока [ампер*виток/вебер] или [виток/генри].

Здесь важно отметить, что фактически магнитодвижущая сила (МДС) имеет принципиальное отличие от электродвижущей силы (ЭДС), которое заключается в том, что непосредственно в магнитном потоке никакие частицы не движутся, тогда как ток, возникающий под действием ЭДС, предполагает движение заряженных частиц, например электронов в металлических проводниках. Однако представление о МДС помогает решать задачи расчета магнитных цепей.

Рассмотрим, например, неразветвленную магнитную цепь, в которую входит ярмо площадью поперечного сечения S, одинаковой по всей длине, при этом материал ярма имеет магнитную проницаемость мю.

Поскольку магнитный поток внутри ярма и внутри зазора имеет одну и ту же величину (в силу непрерывности линий магнитной индукции), то расписав Ф = BS и B=мю*H, распишем напряженности магнитного поля более подробно, а затем подставим в вышеприведенную формулу:

Легко видеть, что подобно ЭДС в законе Ома для электрических цепей, МДС

играет здесь как-бы роль электродвижущей силы, а магнитное сопротивление

роль сопротивления (по аналогии с классическим Законом Ома).

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

4 Магнитодвижущие силы обмоток переменного тока

В-4 Магнитодвижущие силы (МДС) обмоток переменного тока

МДС катушки (фазы сосредоточенной обмотки)

На рис. В-10, а схематически изображено сечение четырехполюсной машины с уложенной в пазы статора фазой сосредоточенной двухслойной обмотки. Катушечная группа такой обмотки состоит из одной катушки и q₁ = 1. При диаметральном шаге у₁ = τ активные стороны катушек соседних полюсов расположены в одних пазах в два слоя и образуют периодическую систему катушек. В проводе каждой катушки течет ток параллельной ветви i_a = i/a₁, полный ток катушки равен i_aw_К. Направление силовых линий магнитного поля, образованного токами катушек, определяется правилом “правого” винта или “буравчика”. Токи в катушках обмотки статора создают четыре полюса магнитного поля, большая часть линий индукции которого В замыкается между соседними полюсными делениями по сердечникам статора и ротора, пересекая зазор машины δ.

Вследствие повторяемости с периодом 2τ (рис. В-11, а) достаточно рассмотреть магнитное поле, образованное двумя катушками соседних полюсных делений. Так как зазор δ много меньше внутреннего диаметра D₁ статора можно пренебречь кривизной статора и заменить кольцевой зазор плоским Начало отсчета совмещено с осью одной из катушек.

Для упрощения пренебрегаем влиянием раскрытий пазов и считаем зазор равномерным. Принимаем магнитную проницаемость стали μ_СТ = ∞, тогда напряженность магнитного поля в стали Н_СТ = В/μ_СТ = 0. При этих условиях сталь сердечников не влияет на магнитное поле машины, карт-на которого определяется только размерами и формой зазора.

Связь напряженности магнитного поля и токов катушек определена законом полного тока. Контур интегрирования выбран совпадающим с силовой линией магнитного поля. В этом случае

Рекомендуемые файлы

, (В-32)

где Н_δ и Н_СТ – напряженности магнитного поля в зазоре и в стали, Н_СТ = 0 и Σ∫H_СТdl_СТ = 0 при μ_СТ = ∞; dl и dl_CT – элементы длины контура интегрирования в зазоре (dl = δ) и стали сердечников; F = 2i_aw_К – магнитодвижущая сила (МДС) фазы, приходящаяся на два полюса машины.

Изменение ширины контура интегрирования от 0 до 2τ не меняет МДС F = 2 i_aw_К = const. При увеличении ширины контура интегрирования до 2τ + Δ > 2τ, где малая величина Δ→ 0 МДС F = ∫Hdl = Σ i = 0. Следовательно, при переходе через паз с током МДС F изменяется на величину полного тока паза –2i_aw_К, представляющего собой сумму токов двух крайних пазов с токами – i_aw_К.

Поэтому МДС F изменяется дважды в противоположных направлениях на границах двух полюсных делений на величину |2i_aw_К| и в пределах двух полюсных делений представляет собой прямоугольную волну

(В-33)

Напряженность магнитного поля в зазоре из формулы (В-36)

. (В-34)

Индукция магнитного поля в зазоре

, (В-35)

где μ₀ – магнитная проницаемость вакуума, μ₀ = 4π·10 – 7 Г/м = const.

Распределение индукции магнитного поля В_δ в равномерном зазоре (δ = const) повторяет форму МДС обмотки, при μ_СТ = ∞ вся эта МДС расходуется на проведение магнитного потока через зазор, имеющий большое магнитное сопротивление.

В реальных машинах магнитная проницаемость стали μ_СТ конечна и напряженность стальных участков Н_СТ > 0. Поэтому часть МДС фазы F в (В-32), равная F_СТ = Σ ∫ H_СТ dl_СТ, тратится на проведение магнитного потока по стальным сердечникам машины. Из-за насыщения стали зависимость В_СТ = f (H_СТ) нелинейна и F_СТ не пропорциональна индукции в стали.

Следовательно, в общем случае индукция магнитного поле в зазоре определяется не только размерами зазора и МДС обмотки, но и насыщением стали магнитопроводов.

При правильно выбранных размерах магнитопроводов и индукции В_δ в зазоре μ_СТ » μ₀ (в 10 – 2 –10 – 4 раз), соответственно Н_СТ = В_СТ /μ_СТ « Н_δ = В_δ /μ₀.

Вследствие относительно большой величины зазора δ синхронных ма-шин, в (В-32) Σ ∫H_СТ dl_СТ 1) гармонических МДС уменьшаются быстрее амплитуды первой гармонической. Следовательно, укорочение шага улучшает форму МДС обмотки.

МДС группы катушек, фазы и трехфазной обмотки

На рис. В-12, а схематически изображена группа из трех (q₁ = 3) последовательно соединенных с полным шагом y₁ = τ, обтекаемых током i_aw_К. Так как при переходе через ток активной стороны каждой катушки МДС изменяется на F_Кm = ± i_aw_К /2 группа катушек образует неподвижную в пространстве ступенчатую волну МДС F_ГР(х) форма которой ближе к синусоиде, чем Фома волны МДС одной катушки.

Следовательно, распределение обмотки по пазам (q₁ > 1) улучшает форму МДС (как и ЭДС) обмотки. На рис. В-12, б изображены первые гармонические МДС катушек F_К1,1, F_К1,2, F_К1,3 с амплитудой F_К1m. Вследствие смещения катушек на геометрический угол (или электрический угол α = рα_Г) амплитуды первых гармонических МДС катушек не совпадают. Поэтому амплитуда первой гармонической МДС группы F_ГР1m меньше арифметичскойсуммы амплитуд МДС трех катушек (или сосредоточенной обмотки с числом витков 3w_К) 3F_К1m (рис. 2.19, б), то есть распределение обмотки по пазам уменьшает амплитуды гармонических МДС.

Синусоидальные первые гармонические МДС можно рас-сматривать как пространствен-ные векторы F_К1,1, F_К1,2, F_К1,3, смещенные на электрический угол α (рис.В-12, в) подобно векторам синусоидально изменяющихся во времени ЭДС Ė_1,К1, Ė_1,К2, Ė_1,К3, сдвинутым по фазе на угол α на рис. 2.19, г и 2.7, б практически совпадают, поэтому уменьшение гармонических МДС за счет распределения обмотки, учитывают коэффициентом распределения k_Р1 = | F_ГР1 | /(q₁F_К1m), определяемым по формуле

. (В-39)

Все сказанное выше справедливо для любой гармонической МДС, и амплитуда любой гармонической МДС катушечной группы

. (В-40)

Очевидно, все сделанные ранее выводы о возможности преставления МДС катушки при наличии в ней переменного тока в виде бесконечных сумм пульсирующих или встречно вращающихся волн нечетных порядков справедливы и для катушечной группы, питаемой переменным током.

Отмеченное выше улучшение формы МДС группы катушек достигается за счет более быстрого уменьшения коэффициентов распределения k_Рν (по сравнению с k_Р1) и соответственно амплитуд F_ГРνm высших гармонических МДС (ν > 1).

Исключение составляют высшие гармонические МДС порядков

, где k = 1, 2, 3… (В-41)

Пространственный период первой (k = 1) из этих гармонических 2τ

примерно равен зубцовому делению статора t_Z1 = πD₁/z₁. Поэтому гармонические порядков ν_Z называют “зубцовыми”. Для этих гармонических электрический угол α между соседними пазами

(В-42)

равен электрическому углу α = рα_Г по основной гармонической. Поэтому диаграмма “зубцовых” гармонически МДС совпадает с диаграммой первых гармонических и коэффициенты распределения k_Р = ±k_Р1, то есть распределение обмотки не уменьшает “зубцовые” гармонические МДС (как и ЭДС “зубцовых” порядков).

Для малых q₁ “зубцовые” гармонические МДС имеют низкий порядок. Так, у сосредоточенных обмоток (q₁ = 1) все высшие гармонические МДС порядков ν = 5, 7, 11, 13,… “зубцовые”. При малых значениях ν_Z амплитуды “зубцовых” гармонических МДС велики и ухудшают форму МДС группы катушек и всей обмотки. Для ослабления гармонических МДС “зубцовых” порядков в синхронных машинах большой мощности применяют распределенные обмотки с целым q₁ ≥ 3.

Амплитуда пульсирующей гармонической МДС фазы двухслойной обмотки

. (В-43)

МДС фазы F_Ф, определяемая суммой МДС катушечных групп, обладает теми же свойствами, что и МДС катушечных групп и катушек, составляющих эти группы. Поэтому МДС обмотки фазы, обтекаемой переменным током, F_Ф представляет собой неподвижную в пространстве пульсирующую с частотой тока ω₁ волну ступенчатой формы (рис. В-12, а), все нечетные гармонические составляющие волны МДС с обратно пропорциональнми номеру гармонической амплитудами F_Фνm ≡ 1/ν достигают максимума на оси фазы и пульсируют с одинаковой частотой ω_ν = ω₁:

. (В-44)

Симметричная трехфазная обмотка (m = 3), питаемая симметричной трехфазной системой синусоидального переменного тока частотой f₁,:

1. Образует прямовращающуюся (вправо) основную или первую гармоническую МДС F₁ с амплитудой

; (В-45)

линейной скоростью вращения

(В-46)

2. Не образует третьих и кратных трем гармонических МДС (F₃ = F₉ = F₁₅ = …= 0).

3. Образует высшие нечетные гармонические МДС F_ν порядков

, где k = 1, 2, 3,… (В-47)

(В-48)

Высшие гармонические порядка ν = 6k + 1 (ν = 7, 13, 19,…) вращаются в том же направлении, что и основная гармоническая МДС, поэтому их называют прямыми или прямовращающимися.

Источник

Чем определяется величина мдс катушки

Магнитодвижущей силой (МДС) или намагничивающей силой (НС) катушки или обмотки с током называют произведение числа витков катушки до на протекающий по ней ток

МДС вызывает магнитный поток в магнитной цепи подобно тому, как ЭДС вызывает электрический ток в электрической цепи. Как и ЭДС, МДС — величина направленная (положительное направление на схеме обозначают стрелкой).

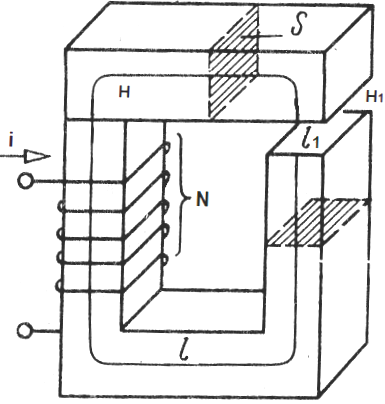
Положительное направление МДС совпадает с движением острия правого винта, если винт вращать по направлению тока в обмотке.

Для определения положительного направления МДС пользуются мнемоническим правилом: если сердечник мысленно охватить правой рукой, расположив ее пальцы по току в обмотке, а затем отогнуть большой палец, то последний укажет направление МДС.

На рис. 14.5 дано несколько эскизов с различным направлением намотки катушек на сердечник и различным направлением МДС.

Источник

Магнитодвижущая сила сосредоточенной обмотки

При анализе МДС обмоток будем исходить из следующего:

а) МДС обмоток переменного тока изменяется во времени и вместе с тем распределена по перимет­ру статора, т. е. МДС является функцией не только времени, но и пространства;

б) ток в обмотке статора синусоидален, а следо­вательно, и МДС обмотки является синусоидальной функцией времени;

в) воздушный зазор по периметру статора по­стоянен, т. е. сердечник ротора цилиндрический;

г) ток в обмотке ротора отсутствует, т. е. ротор не создает магнитного поля.

Рассмотрим двухполюсную машину переменного тока с сосредоточенной однофазной катушкой обмот­ки статора с шагом у₁ = τ (рис. 9.1, а). При прохожде­нии тока по этой обмотке возникает магнитный поток, который, замыкаясь в магнитопроводе, дважды пре­одолевает зазор σ между статором и ротором.

F_k = 0,5 I_max ω_k = 0,5 I₁ ω_k (9.1)

где I₁ — действующее значение тока катушки.

Для сосредоточенной обмотки МДС можно раз­ложить в гармонический ряд, т. е. представить в ви­де суммы МДС, имеющих синусоидальное распре­деление в пространстве:

где α —пространственный угол (рис. 9.1, б).

Из (9.2) следует, что МДС сосредоточенной обмотки стато­ра содержит основную и высшие нечетные гармоники, амплитуды которых обратно пропорциональны порядку гармоники υ.

Рассмотренные нами в предыдущих главах гармонические составляющие тока и ЭДС называют временными гармониками. Временная периодичность у этих гармоник определяется номером гармоники (7.6).

Рис. 9.1. МДС однофазной сосредоточенной обмотки статора

Амплитуда первой пространственной гармоники МДС по (9.2)

F_k1 = F_k = I₁ ω_k = 0,9 I₁ ω_k (9.3)

Амплитуда пространственной гармоники υ-гo порядка

Зависимость МДС любой гармоники от времени и пространственного угла α определяется выражением

С увеличением номера гармоники растет ее пространственная периодичность. Поэтому число полюсов пространственной гармо­ники МДС равно 2p_v = 2pυ.

Полезный магнитный поток в машине переменного тока создает основная гармоника МДС, а высшие пространственные гар­моники МДС обычно оказывают на машину вредное действие (действие высших гармоник МДС рассмотрено в последующих главах).

Магнитодвижущая сила распределенной обмотки

На рис. 9.2, а показана катушечная группа обмотки статора, состоящая из трех катушек. График МДС основной гармоники каждой из этих катушек представляет собой синусоиду,

максимальное значение которой (F_к1) совпадает с осью соответствующей катушки, поэтому между векторами МДС катушек F_1k1, F_2k1 и F_3k1 имеется пространственный сдвиг на угол γ’, равный пазовому углу смещения катушек обмотки относительно друг друга γ’.

График МДС основной гармоники всей катушечной группы представляет собой также

синусоиду, полученную сложением ординат синусоид МДС катушек, составляющих катушечную группу. Максимальное значение этого графика F_г1 совпадает с осью средней катушки.

Рис. 9.2. МДС основной гармоники

распределенной обмотки статора

Если все катушки катушечной группы сосредоточить в двух пазах (γ’ = 0), то результирующая МДС будет определяться арифметической суммой МДС катушек, т.е. F_r1 = F_k1 q₁.

Таким образом, распределение катушек в нескольких пазах ведет к уменьшению МДС катушечной группы, которое учитыва­ется коэффициентом распределения обмотки (см. § 7.3). Для МДС основной гармоники это уменьшение невелико, но для высших пространственных гармоник оно значительно.

Амплитуда пространственной гармоники катушечной группы распределенной обмотки

где k_pv — коэффициент распределения.

Источник