Чем определяется точность следящей системы

Точность системы управления

АНАЛИЗ СИСТЕМ УПРАВЛЕНИЯ

Требования к управлению

В задаче стабилизации наиболее важны свойства установившегося режима. Для следящих систем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки).

В целом можно выделить четыре основных требования:

• точность– в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую;

• устойчивость– система должна оставаться устойчивой на всех режимах, не должна идти «вразнос» (корабль не должен идти по кругу при смене курса);

• качество переходных процессов– при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;

• робастность– система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировании.

Процесс на выходе

Ниже представлен способ, как вычислить процесс на выходе системы с передаточной функцией W(s) при входном сигнале, для которого известно изображение по Лапласу X(s).

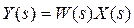
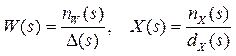
При нулевых начальных условиях изображение выхода равно . Предположим, что W(s) и X (s) – рациональные функции, то есть их можно представить в виде отношения полиномов

.

Для простоты считаем, что полиномы Δ(s) и d_X(s) имеют только простые вещественные корни, поэтому

,

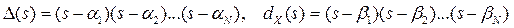
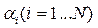
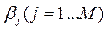
причем общих корней у них нет. Числа и называются полюсами функций W(s) и X(s) соответственно.

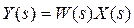
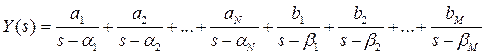
При этих условиях произведение можно разложить на простые дроби

.

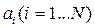
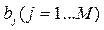
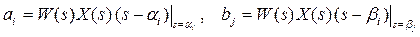
Здесь и – постоянные, которые в данном случае определяются по формулам

.

Далее мы предположим, что произведение W(s) X (s) несократимо. В этом случае все числа a_i и b_j не равны нулю.

Чтобы найти выход y(t), нужно вычислить обратное преобразование Лапласа для Y(s). По таблицам находим

. (1)

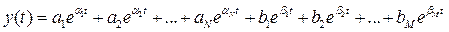
Функция e λ t при t →∞ стремится к нулю, если λ 0. Поэтому выражение (1) позволяет сделать следующие выводы:

• сигнал на выходе системы зависит как от свойств передаточной функции системы, так и от входного сигнала;

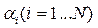
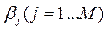
• для того чтобы переходный процесс затухал (функция y(t) стремилась к нулю), все числа и должны быть отрицательными (иметь отрицательные вещественные части);

• если один из полюсов W(s) или X(s) равен нулю, y(t) может иметь постоянную (незатухающую) составляющую;

• если хотя бы один из полюсов W(s) или X(s) больше нуля (имеет положительную вещественную часть), выход системы неограниченно растет.

Важна несократимость произведения W(s)X(s), иначе некоторые коэффициенты a_i и/или b_j могут оказаться нулевыми и соответствующие экспоненты «исчезают» из формулы (1). Тогда, например, может оказаться, что выход не «уходит в бесконечность» даже если W(s) или X(s) имеет полюс с положительной вещественной частью (и он сократился в произведении W(s) X(s)).

Точность системы управления

Точность системы обычно оценивается для одного из эталонных входных сигналов. Это может быть, например, единичный скачок

,

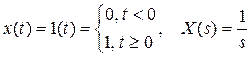
или линейно возрастающий сигнал

,

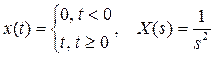
или гармонический сигнал с частотой ω

.

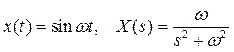
Точность системы в установившемся режиме определяется ошибкой e(t) или ее изображением E(s). Для ее исследования используют передаточную функцию по ошибке W_e(s), которая связывает изображения ошибки и входного сигнала

. (2)

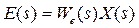
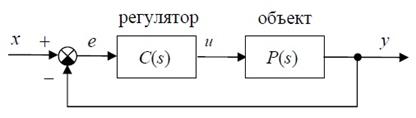
Рассмотрим контур управления, состоящий из регулятора и объекта

Представим передаточные функции C(s) и P(s), а также изображение входа X(s) в виде отношения полиномов

.

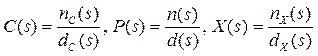
В данном случае передаточная функция по ошибке равна

,

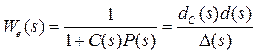
где 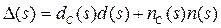– характеристический полином замкнутой системы.

Рассмотрим реакцию системы на единичный ступенчатый входной сигнал, изображение которого равно X(s) = 1/s. Сигнал ошибки определяется полюсами передаточной функции W_e(s)(то есть корнями характеристического полинома Δ(s)) и полюсами изображения X(s). На практике все полюса W_e(s) должны иметь отрицательные вещественные части, иначе система будет неустойчивой. Поэтому нулевых полюсов у функции W_e(s) быть не может. Тогда

.

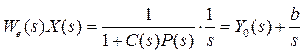
Здесь изображение Y₀(s)имеет полюса только с отрицательной вещественной частью, а постоянная b рассчитывается по формуле разложения на простые дроби

.

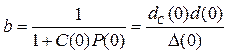
После затухания всех экспонент с отрицательными показателями получим .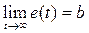

Для того чтобы сделать нулевой статическую ошибку, достаточно обеспечить 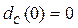(то есть регулятор должен содержать интегратор) или d(0) = 0 (объект содержит интегратор).

Этот результат можно обобщить для любых незатухающих входных сигналов, изображения которых имеют полюса на мнимой оси (в точке s = 0 или в точках s = ± jω). Для того чтобы ошибка стремилась к нулю при t →∞ необходимо, чтобы эти полюса сократились в произведении

.

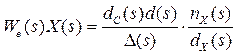
А это, в свою очередь, возможно только тогда, когда они являются корнями полинома d_C(s)d(s), то есть, внутри системы есть модель входного сигнала. Этот принцип называется принципом внутренней модели.

Например, для точного отслеживания ступенчатого сигнала нужно, чтобы объект или регулятор содержали интегрирующее звено (с передаточной функцией 1/s). Тогда произведение d_C(s)d(s) имеет сомножитель s, и полюс X(s) в точке s = 0 сократится в произведении W_e(s)X(s). Таким образом, если передаточная функция разомкнутого контура C(s)P(s) содержит множитель s в знаменателе, обеспечивается нулевая ошибка слежения за постоянным сигналом (нулевая статическая ошибка). Поэтому такую систему называют астатической.

Для отслеживания линейно возрастающего сигнала в контуре должно быть уже два интегратора (нужно сократить двойной полюс X(s) в точке s = 0). Такая система обладает астатизмом второго порядка. В общем случае система, в которой

,

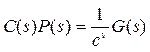
где ν > 0 – натуральное число и функция G(s) не имеет нулей и полюсов в точке s = 0, называется астатической системой ν-ого порядка. Такая система в установившемся режиме без ошибки отслеживает сигнал вида

,

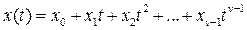
при любых значениях коэффициентов .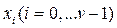

Казалось бы, для повышения точности можно поставить много интеграторов, и все проблемы будут решены. Но при этом нужно учесть, что мы говорили только о точности в установившемся режиме, не затрагивая переходные процессы и вопросы устойчивости. Добавление каждого нового интегратора ухудшает переходные процессы, осложняет стабилизацию системы, снижает быстродействие. Например, двойным интегратором в принципе невозможно управлять с помощью простого регулятора-усилителя (так называемого пропорционального регулятора или П-регулятора). Кроме того, если разомкнутая система включает два интегратора и более, для сигнала ошибки e(t) справедливо ограничение

.

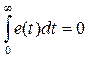
Поскольку интеграл от ошибки равен нулю, часть времени ошибка должна быть положительной, а часть – отрицательной. Поэтому при любом управлении не удастся получить монотонный переходный процесс (когда сигнал выхода подходит к заданному значению «с одной стороны», как у апериодического звена).

Для стохастической системы, в которой все процессы имеют случайный характер, точность оценивается с помощью математического ожидания и дисперсии ошибки.

Дата добавления: 2017-05-18 ; просмотров: 1467 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Классификация и виды следящих систем. Задачи и этапы проектирования следящих систем

Страницы работы

Содержание работы

Современные системы автоматического управления нашли самое широкое применение в различных областях народного хозяйства. Это связано не только с необходимостью автоматизации различных технологических процессов и производственных операций, но и с появлением принципиально новых автоматизированных машин, предназначенных для работы в экстремальных условиях: в космосе, под водой, в зонах с ядерным излучением, в шахтах, в агрессивных средах и т.п.

Высокие требования, предъявляемые к динамическим характеристикам систем автоматического управления, обуславливают необходимость учитывать при их проектировании влияние зазоров и упругих деформаций, сухого и вязкого трения в силовом редукторе, переменность моментов инерции нагрузки, внешние возмущения и т.д. Это особенно важно для автоматических систем большой мощности и систем со многими степенями свободы.

Таким образом специфика объекта регулирования выдвигает ряд новых проблем при проектировании автоматических систем.

Из всего многообразия систем автоматического регулирования в данном курсе выделяется лишь класс следящих систем, при этом общие вопросы проектирования рассматриваются на конкретных примерах, что, не нарушая общности выводов, позволяет изложить инженерные методики проектирования современных, сложных по своей структуре, высококачественных следящих систем.

Проектирование современных систем автоматики немыслимо без применения цифровой и аналоговой техники. Этим вопросам в настоящем курсе также уделяется должное внимание. Важным этапом проектирования является синтез структурной схемы следящей системы, выбор и согласование необходимых элементов и их параметров, оценка статической и динамической точности системы, определение необходимости введения коррекции, расчет корректирующих устройств.

ГЛАВА I. КЛАССИФИКАЦИЯ И ВИДЫ СЛЕДЯЩИХ СИСТЕМ

1.1. Классификация следящих систем (СС)

Широкий диапазон применения, разнообразие функционального построения и математического описания следящих систем в значительной мере осложняют их классификацию. Трудности определения общего критерия классификации следящих систем неизбежно приводят к “многомерной” классификационной структуре. Следящие системы можно классифицировать по способу формирования управляющего воздействия, характеру сигнала рассогласования, способу математического описания СС и характеру контролируемых изменений, проходящих в следящих системах.

С позиций проектирования приведенные признаки классификации не являются достаточными, т.к. не учитывают особенностей следящих систем в зависимости от их назначения и условий работы, вида исполнительных устройств и принципа их действия.

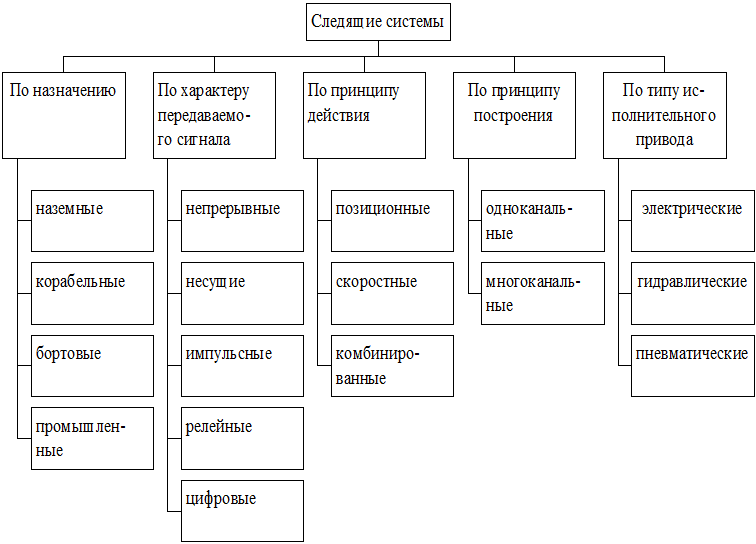
С учетом сказанного все многообразие СС модно классифицировать по основным признакам, связанным с принципами построения и действия, спецификой работы и т.д. (рис. 1.1).

Динамические свойства СС и законы изменения управляющих и возмущающих воздействий во многом зависят от назначения объекта управления в целом и функций, выполняемых СС, а также от условий работы.

По условиям работы СС подразделяются на наземные, корабельные, бортовые и промышленные. Наземные системы, в свою очередь, можно разделить на стационарные и подвижные. В сравнительно благоприятных условиях находятся наземные стационарные системы, которые, как правило, имеют стационарное питание, не имеют жестких ограничений по массе и габаритным размерам. В наиболее тяжелых климатических условиях работают лишь элементы систем, располагаемых на открытом воздухе. К этой группе можно отнести, например, следящие системы, обеспечивающие слежение за подвижными объектами: следящие системы антенн радиолокационных станций автоматического сопровождения, координаторов и т.п.

Требования к динамике таких систем определяются законом движения цели и условиями получения оптической фильтрации случайной составляющей сигнала. Часто приходится учитывать и значительные возмущения в виде “ветрового момента”.

К наземным подвижным системам предъявляют более жесткие требования по механическим воздействиям, массе и габаритным размерам. Источники питания подвижных систем могут иметь ограниченную мощность и характеристики, изменяющиеся в широком диапазоне.

Характерным примером систем этой группы являются следящие системы подвижных артиллерийских установок. Динамические свойства этих СС определяют в основном исходя из законов движения цели и обеспечения условий наилучшей фильтрации случайной составляющей входного сигнала. Для них характерно наличие больших и быстро меняющихся во времени (ударных) моментов нагрузки.

Для колебательных систем характерна более агрессивная внешняя среда и повышенный уровень механических нагрузок (вибрационных и ударных). Указанные системы объединяет работа при качке и наличии значительного уровня помех во входном сигнале. Кроме того, общим является требование высокого быстродействия при весьма жестких ограничениях габаритных размеров и энергопотребления исполнительных устройств. К этой группе относятся различные приборные СС, а также системы наведения и стабилизации антенны РЛС, орудийных башен, стабилизированных постов и т.д.

Источник

Лекция 2.4. Динамическая точность линейных стационарных следящих систем при неслучайных воздействиях

Под динамической точностью следящей системы понимается разность входной и выходной переменных в каждый момент времени. Данная разность переменных системы является первичным сигналом управления системы и называется динамической ошибкой системы. Точность следящей системы характеризуется величиной динамической ошибки. Поскольку динамическая ошибка является координатой (переменной) линейной системы, то, в соответствии с принципом суперпозиции, может быть получена, как сумма отдельных составляющих, каждая из которых связана с конкретным воздействием.

Исследуем динамическую ошибку системы, вызванную входным (управляющим) воздействием.

Согласно Рис., изображение динамической ошибки равно:

-передаточная функция ошибки системы относительно входного воздействия.

Если ПФ разомкнутой системы представлена в виде:

При нулевых начальных условиях динамическая ошибка системы при детерминированном воздействии описывается частным решение этого дифференциального уравнения.

Если система устойчива, то такое решение содержит, затухающую со временем, переходнуюсоставляющую динамической ошибки и установившуюся составляющую ошибки, которая существует до тех пор пока существует воздействие.

Обе данные составляющие ошибки характеризуют вынужденную динамическую ошибку системы.

Таким образом, динамическая ошибка системы, при нулевых начальных условиях, определяется суммой:

Иллюстрация приведена на Рис.

Точное описание такой динамической ошибки получается после решения дифференциального уравнения ошибки.

Помимо входного( полезного) воздействия на систему действуют возмущения, которые являются причинами дополнительных составляющих динамической ошибки.

Например, согласно структурной схеме Рис. и принципа суперпозиции, справедливого для линейной системы можно записать выражение для изображения полной (суммарной)ошибки системы:

В качестве примера, рассмотрим следящую систему с тремя воздействиями Рис.. Для определения отдельных передаточных функций ошибки используем преобразование структурной схемы, заключающееся в том, что структурная схема преобразуется так, чтобы входной переменной было рассматриваемое воздействие, а выходной – динамическая ошибка от данного воздействия.

Определим составляющую динамической ошибки от возмущения на входе системы. Рис..

Используя формулу замыкания контура, получаем:

Заметим, что данное возмущение преобразуется в ошибку системы той же ПФ (отличается только знак),что и входное управляющее воздействие в выходную координату системы.Поэтому, желание приблизить динамику системы к идеальной в отношении воспроизведения входного (полезного) воздействия одновременно увеличивает составляющую динамической ошибки от данного возмущение. Следовательно, существует техническое противоречие, которое можно разрешить только путем компромисса. В любом случае этопротиворечие ограничивает динамическую точность.

Определим составляющую динамической ошибки от возмущения, действующего на выходе. Проведем преобразование структурной схемы к причинно-следственному виду Рис. и определим ПФ замкнутого контура. Получаем:

-различные требования к величине допустимых составляющих динамической ошибки;

-различную динамику воздействий:

— сохранение желаемого запаса устойчивости.

В условиях одноконтурной структуры следящей системы такое компромиссное решение, особенно, при высоком требовании к точности системы, весьма затруднительно.

Суммируя составляющие вынужденной динамической ошибки системы от рассмотренных воздействий, получаем выражение для изображения полной динамической ошибки системы:

Данное выражение можно использовать для определения как переходной, так и установившейся составляющих динамической ошибки системы.

Рассмотрим установившуюся динамическую ошибку следящей системы при гармонических воздействиях

Для определения установившейся динамической ошибки в этом случае удобно использовать частотные характеристики ошибки. Динамическая ошибка линейной системы на гармоническое воздействие, согласно особому свойству линейной стационарной системы, является гармонической функцией той же частоты.

При анализе динамической ошибки при таком воздействии интерес представляет ее амплитуда – максимальное значение. Поэтому для определения динамической ошибки достаточно использовать только амплитудно-частотные характеристики (ЛАХ).

Так, получим ЛАХ ошибки от входного (полезного) воздействия.

Пусть, в качестве примера, ПФ разомкнутой системы имеет типовой, для систем среднего класса точности, вид:

Построим ЛАХ разомкнутой системы и рассмотрим ее связь с ЛАХ ошибки от входного воздействия Рис.

Пересечение нижней прямой с ЛАХ определяет диапазон частот, в котором характеристики замкнутой системы близки к характеристиками разомкнутой системы так, как действие обратной связи здесь не эффективно (высоко-частотный диапазон частот).

Область частот расположенная между ближайшими пределами, указанных диапазонов, относится к среднему диапазону частот разомкнутой системы (поведение ЛАХ в этом диапазоне связано с запасом устойчивости системы.)

Учитывая ранее полученное выражение для ПФ ошибки относительно входного управляющего воздействия, получаем:

В области низких частот и поэтому, согласно свойству глубокой отрицательной обратной связи, справедливо приближенное равенство:

Источник