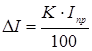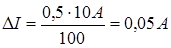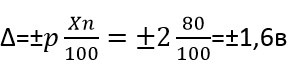Чем определяется точность измерения данного прибора
V. Точность измерительных приборов.
Точность измерительного прибора – это его свойство, характеризующее степень приближения показаний данного измерительного прибора к действительным значениям измеряемой величины и определяется той наименьшей величиной, которую с помощью этого прибора можно определить надёжно.
Точность прибора зависит от цены наименьшего деления его шкалы и указывается или на самом приборе, или в заводской инструкции (паспорте). Заметим, что точность измерений 


Погрешность электроизмерительных приборов определяется классом точности (или приведенной погрешностью Епр), который указывается на лицевой стороне прибора соответствующей цифрой в кружке. Классом точности прибора К называют выраженное в процентах отношение абсолютной погрешности 

Зная класс точности и предел измерения прибора, можно рассчитать его абсолютную погрешность:

Эта погрешность одинакова для любого измерения сделанного с помощью данного прибора. Классов точности семь: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Приборы первых трех классов точности (0,1; 0,2; 0,5) называются прецизионными и используются при точных научных измерениях, приборы остальных классов точности называются техническими. Приборы без указания класса точности считаются внеклассными.
Пример. Сила тока измеряется в цепи амперметром, класс точности которого К=0,5, а шкала имеет предел измерения Iпр=10 А. Находим абсолютную погрешность амперметра:
Отсюда следует, что амперметр позволяет измерять силу тока с точностью не более 0,05 А, и поэтому нецелесообразно делать отсчёт по шкале прибора с большей точностью.
Допустим, что с помощью данного амперметра были измерены три значения силы тока: I1=2 А; I2=5 А; I3=8 А. Находим для каждого случая относительную погрешность: 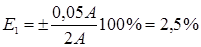
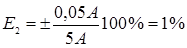
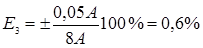
Из этого примера следует, что в третьем случае относительная погрешность самая маленькая, то есть чем больше величина отсчёта по прибору, тем меньше относительная погрешность измерения. Вот почему для оптимального использования приборов рекомендуется их подбирать так, чтобы значение измеряемой величины находилось в конце шкалы прибора. В этом случае относительная погрешность приближается к классу точности прибора. Если точность прибора неизвестна, то абсолютная погрешность принимается равной половине цены наименьшего деления (линейка, термометр, секундомер). Для штангенциркуля и микрометра – точность их нониусов (0,1 мм, 0,01 мм).
Примечания: 1) При отсчетах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для устранения так называемой ошибки параллакса на многих приборах устанавливается зеркало («зеркальные приборы»). Глаз экспериментатора расположен правильно, если стрелка прибора закрывает свое изображение в зеркале.
2) При косвенных измерениях (например, определение объема цилиндра по его диаметру и высоте) следует определять все измеряемые вершины с приблизительно одинаковой относительной точностью.
3) При обработке результатов измерений следует помнить, что точность вычислений должна быть согласована с точностью самих измерений. Вычисления, произведенные с большим, чем это необходимо, числом десятичных знаков, приводят к большому объему ненужной работы. Например, если хотя бы одна из величин в каком-либо выражении определена с точностью до двух значащих цифр, то нет смысла вычислять результат с точностью, большей двух значащих цифр. В тоже время в промежуточных расчетах рекомендуется сохранять одну лишнюю цифру, которая в дальнейшем – при записи окончательного результата – будет отброшена. В теории погрешностей из существующих правил округления имеется следующее исключение: при округлении погрешностей последняя сохраняемая цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше 3.
4) Примеры окончательной записи результатов измерений:
Что нужно знать о классе точности измерительного прибора?
Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.
В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.
Что такое класс точности
Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».
Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.
Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.
Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.
Абсолютная погрешность рассчитывается следующим образом:
∆=±a или ∆=(a+bx)
x – число делений, нормирующее значение величины
a, b – положительные числа, не зависящие от х
Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже
Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.
Каким ГОСТом регламентируется точность приборов?
ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.
Как определить класс точности электроизмерительного прибора, формулы расчета
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.
Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12
Находим относительную погрешность:
Y= 100×0,025/12=0,208 или 2,08%
(вывод: класс точности – 2,5).
Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:
Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12
Предел абсолютной допустимой погрешности:
Относительная погрешность одного деления:
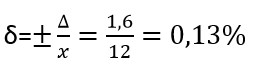
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.
Поверка приборов, для чего она нужна
Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.
Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.
Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.
Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.
Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.
Видео на тему относительная погрешность прибора
Заключение
Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.
Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.
Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: 

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
На точность измерения влияет много факторов, в частности:
Все это необходимо учитывать при проведении измерений.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.
Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.
Решение:
1) Цена деления нижней шкалы:
Цена деления средней шкалы:
Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10° 

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Что такое точность измерения прибора
Точность – измерительный прибор
Точность измерительного прибора определяется степенью достоверности результата измерения. [1]
Точность измерительного прибора определяется степенью приближения результата измерения к фактическому значению измеряемой величины. [2]
Точность измерительного прибора определяется степенью приближения результата измерения к действительному значению измеряемой величины. Отклонение измеренного значения от действительного называется погрешностью измерения. Погрешность измерения выражается абсолютной или относительной величиной. [3]
Точность измерительных приборов и правильное выполнение первой и третьей операций очень важны, без этого невозможно получить точные результаты анализа. Однако, когда говорят о том или другом методе анализа, имеют в виду прежде всего определенную реакцию или последовательность реакций. Поэтому разделение методов химического количественного анализа на отдельные группы связано с химической реакцией. Прежде всего принимается во внимание способ использования реакции и затем тип химической реакции. [4]
Точность измерительного прибора определяется его основной погрешностью или классом точности. Основная погрешность при измерении токов и напряжений выражается в процентах от номинального ( наибольшего) значения шкалы прибора. [5]
Точность измерительных приборов и правильное выполнение первой и третьей операций очень важны, без этого невозможно получить точные результаты анализа. Однако, когда говорят о том или другом методе анализа, имеют в виду прежде всего определенную реакцию или последовательность реакций. Поэтому разделение методов химического количественного анализа на отдельные группы связано с химической реакцией. Прежде всего принимается во внимание способ использования реакции и затем тип химической реакции. [6]
Точность измерительного прибора в большинстве случаев указывается в заводском паспорте, прилагаемом к прибору. [7]
Точность измерительного прибора определяется степенью приближения результата измерения к действительному значению измеряемой величины. Отклонение измеренного значения от действительного называется погрешностью измерения. Погрешность измерения выражается абсолютной или относительной величиной. [8]
Точностью измерительного прибора называется та наименьшая величина, которую можно вполне надежно определить с помощью данного прибора. [9]
Точностью измерительного прибора называют степень достоверности результатов измерения, оцениваемую путем указания положительного или отрицательного пределов () наибольшей возможной погрешности. [10]
Класс точности измерительного прибора определяется наибольшей допустимой погрешностью в процентах величины, соответствующей предельному значению шкалы прибора. [12]
Характеристиками точности измерительного прибора являются также вариация показаний и порог чувствительности. [13]
Класс точности измерительного прибора – это число, которое соответствует наибольшей погрешности, допустимой нормами. Класс точности выражается в процентах от верхнего предела измерения прибора. Например, термометр класса 1 может иметь допустимую погрешность 1 % от верхнего предела шкалы. [14]
Классом точности измерительного прибора называется его характеристика, которая определяет степень точности измерения, пределы основной погрешности. Для приборов теплотехнического контроля холодильных установок класс точности численно равен максимальной величине приведенной основной погрешности, выраженной в процентах. [15]
Измеряемые величины не могут быть определены абсолютно достоверно. Измерительные инструменты и системы всегда имеют некоторое допустимое отклонение и помехи, которые выражаются степенью неточности. К тому же, необходимо учитывать и особенности конкретных приборов.
В отношении неточности измерений часто используются следующие термины:
Часто эти термины путаются. Поэтому здесь я хотел бы подробно рассмотреть вышеуказанные понятия.
Неточность измерения
Неточности измерения могут быть разделены на систематические и случайные измерительные ошибки. Систематические ошибки вызваны отклонениями при усилении и настройкой «нуля» измерительного оборудования. Случайные ошибки вызваны шумом и индуцированными напряжениями и/или токами.
Погрешность и точность
Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением. Точность относится к случайному разбросу измеряемых величин.
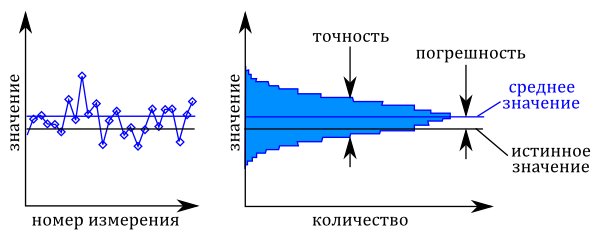
Когда мы проводим некоторое число измерений до момента стабилизации напряжения или же какого-то другого параметра, то в измеренных значениях будет наблюдаться некоторая вариация. Это вызвано тепловым шумом в измерительной цепи измерительного оборудования и измерительной установки. Ниже, на левом графике показаны эти изменения.
Определения неопределенностей. Слева — серия измерений. Справа — значения в виде гистограммы.
Гистограмма
Измеренные значения могут быть изображены в виде гистограммы, как показано справа на рисунке. Гистограмма показывает, как часто наблюдается измеренное значение. Самая высокая точка на гистограмме, это чаще всего наблюдаемое измеренное значение, в случае симметричного распределения равно среднему значению (изображено синей линии на обоих графиках). Черная линия представляет истинное значение параметра. Разница между средним измеренной величины и истинным значением и является погрешностью. Ширина гистограммы показывает разброс отдельных измерений. Этот разброс измерений называется точностью.
Используйте правильные термины
Погрешность и точность, таким образом, имеют различные значения. Поэтому вполне возможно, что измерение является очень точным, но имеющим погрешность. Или наоборот, с малой погрешностью, но не точное. В общем, измерение считается достоверным, если оно точное, и с малой погрешностью.
Погрешность
Погрешность является индикатором корректности измерения. Из-за того, что в одном измерении точность оказывает влияние на погрешность, то учитывается среднее серии измерений.
Погрешность измерительного прибора обычно задается двумя значениями: погрешностью показания и погрешностью по всей шкале. Эти две характеристики вместе определяют общую погрешность измерения. Эти значения погрешности измерения указываются в процентах или в ppm (parts per million, частей на миллион) относительно действуюшего национального стандарта. 1% соответствует 10000 ppm.
Погрешность приводится для указанных температурных диапазонов и для определенного периода времени после калибровки. Обратите внимание, что в разных диапазонах, возможны, и различные погрешности.
Погрешность показаний
Указание процентного отклонения без дополнительной спецификации также относится к показанию. Допустимые отклонения делителей напряжения, точность усиления и абсолютные отклонения при считывании и оцифровке являются причинами этой погрешности.
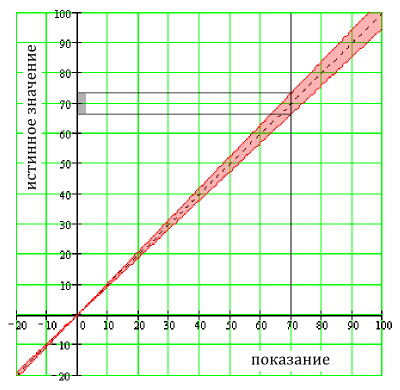
Неточность показаний в 5% для значения 70 В
Вольтметр, который показывает 70.00 В и имеет спецификацию «± 5% от показаний», будет обладать погрешностью в ±3.5 В (5% от 70 В). Фактическое напряжение будет лежать между 66.5 и 73.5 вольтами.
Погрешность по всей шкале
Этот тип погрешности обусловлен ошибками смещения и ошибками линейности усилителей. Для приборов, которые оцифровывают сигналы, присутствует нелинейность преобразования и погрешности АЦП. Эта характеристика относится ко всему используемому диапазону измерений.
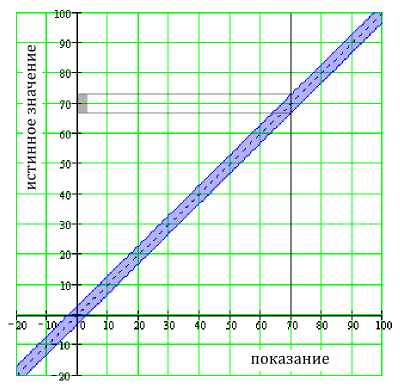
Вольтметр может иметь характеристику «3% шкалы». Если во время измерения выбран диапазон 100 В (равный полной шкале), то погрешность составляет 3% от 100 В = 3 В независимо от измеренного напряжения. Если показание в этом диапазоне 70 В, то реальное напряжение лежит между 67 и 73 вольтами.
Погрешность 3% шкалы в диапазоне 100 В
Погрешность шкалы в цифрах
Часто для цифровых мультиметров приводится погрешность шкалы в разрядах вместо процентного значения.
Вычисление погрешности измерения
Спецификации допустимых отклонений показания и шкалы вместе определяют полную погрешность измерения прибора. Ниже при расчете используются те же значения, что и в приведенных выше примерах:
Точность: ±5% показания (3% шкалы)
Полная погрешность измерения вычисляется следующим образом:
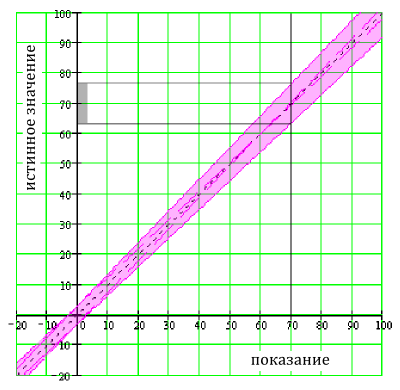
В этом случае, полная погрешность ±6.5В. Истинное значение лежит между 63.5 и 76.5 вольтами. На рисунке ниже это показано графически.
Полная неточность для неточностей показания 5% и 3% шкалы для диапазона 100 В и показания 70 В
Процентная погрешность – это отношение погрешности к показанию. Для нашего случая:
Цифры
Цифровые мультиметры могут иметь спецификацию «± 2.0% показания, + 4 цифры». Это означает, что 4 цифры должны быть добавлены к 2% погрешности показания. В качестве примера снова рассмотрим 3½ разрядный цифровой индикатор. Он показывает 5.00 В для выбранного диапазона 20 В. 2% показания будет означать погрешность в 0,1 В. Добавьте к этому численную погрешность (= 0,04 В). Общая погрешность, следовательно, 0,14 В. Истинное значение должно быть в диапазоне между 4.86 и 5,14 вольтами.
Суммарная погрешность
Зачастую в расчет принимается только погрешность измерительного прибора. Но также, дополнительно следует принимать во внимание погрешности измерительных инструментов, в том случае, если они используются. Вот несколько примеров:
Увеличение погрешности при использовании пробника 1:10
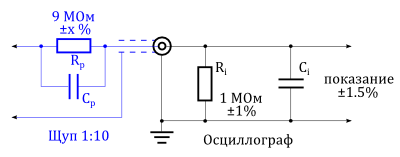
Если в процессе измерений используется щуп 1:10, то необходимо учитывать не только измерительную погрешность прибора. На погрешность также влияет входной импеданс используемого прибора и сопротивление щупа, которые вместе составляют делитель напряжения.
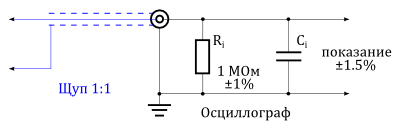
Подключенный к осциллографу щуп 1:1
На рисунке выше схематически показан осциллограф с подключенным к нему пробником 1:1. Если мы рассмотрим этот пробник как идеальный (нет сопротивления соединения), то приложенное напряжение передается прямо на вход осциллографа. Погрешность измерения теперь определяется только допустимыми отклонениями аттенюатора, усилителя и цепями, принимающими участие в дальнейшей обработке сигнала и задается производителем прибора. (На погрешность также влияет сопротивление соединения, которое формирует внутреннее сопротивление 
На рисунке ниже показан тот же самый осциллограф, но теперь ко входу подключен щуп 1:10. Этот пробник имеет внутреннее сопротивление соединения 

Пробник 1:10, подключенный к осциллографу, вносит дополнительную погрешность
Допустимое отклонение входного сопротивления осциллографа может быть найдено в его спецификации. Допустимое отклонение сопротивления соединения щупа 
Предположим, что осциллограф имеет допустимое отклонение 1.5% и используется щуп 1:10 с погрешностью в системе 2.5%. Эти две характеристики можно перемножить для получения полной погрешности показания прибора:
Здесь 


Измерения с шунтирующим резистором
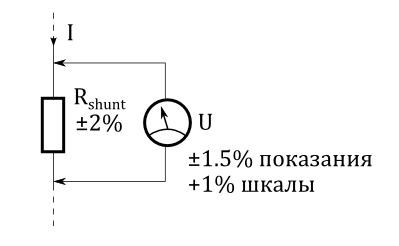
Часто при измерениях токов используют внешний шунтирующий резистор. Шунт имеет некоторое допустимое отклонение, которое влияет на измерение.
Увеличение погрешности при использовании шунтирующего резистора
Заданное допустимое отклонение шунтирующего резистора влияет на погрешность показания. Для нахождения полной погрешности, допустимое отклонение шунта и погрешность показаний измерительного прибора перемножаются:
В этом примере, полная погрешность показания равна 3.53%.
Сопротивление шунта зависит от температуры. Значение сопротивления определяется для данной температуры. Температурную зависимость часто выражают в 
Для примера вычислим значение сопротивления для температуры окружающей среды 





Ток, протекающий через шунт является причиной рассеяния энергии на шунте, что приводит к росту температуры и, следовательно, к изменению значения сопротивления. Изменение значения сопротивления при протекании тока зависит от нескольких факторов. Для проведения очень точного измерения, необходимо откалибровать шунт на дрейф сопротивления и условия окружающей среды при которых проводятся измерения.
Точность
Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.
Распределение Гаусса
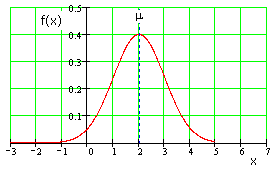
Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:
Здесь 



Распределение вероятностей с 
В таблице указаны шансы получения значений в заданных пределах.
| Граница | Шанс |
| 0.5·σ | 38.3 % |
| 0.674·σ | 50.0 % |
| 1·σ | 68.3 % |
| 2·σ | 95.4 % |
| 3·σ | 99.7 % |
Как видно, вероятность того, что измеренное значение лежит в диапазоне ± 

Повышение точности
Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.
Разрешение
Разрешением, или, как еще говорят, разрешающей способностью измерительной системы является наименьшая различимая измеряемая величина. Определение разрешения прибора не относится к точности измерения.
Цифровые измерительные системы
Цифровая система преобразует аналоговый сигнал в цифровой эквивалент посредством аналого-цифрового преобразователя. Разница между двумя значениями, то есть разрешение, всегда равно одному биту. Или, в случае с цифровым мультиметром, это одна цифра.
Возможно также выразить разрешение через другие единицы, а не биты. В качестве примера рассмотрим цифровой осциллограф, имеющий 8-битный АЦП. Чувствительность по вертикали установлена в 100 мВ/дел и число делений равно 8, полный диапазон, таким образом, равен 800 мВ. 8 бит представляются 2 8 =256 различными значениями. Разрешение в вольтах тогда равно 800 мВ / 256 = 3125 мВ.
Аналоговые измерительные системы
В случае аналогового прибора, где измеряемая величина отображается механическим способом, как в стрелочном приборе, сложно получить точное число для разрешения. Во-первых, разрешение ограничено механическим гистерезисом, причиной которого является трение механизма стрелки. С другой стороны, разрешение определяется наблюдателем, делающем свою субъективную оценку.
Измерение – совокупность операций по применению технического средства, хранящего единицу величины, обеспечивающих нахождение соотношения измеряемой величины с ее единицей в явном или неявном виде и получение значения этой величины. Вообще метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Усовершенствование точности измерений стимулировало развитие наук, предоставляя более достоверные и чувствительные средства исследований. От точности средств измерения зависит эффективность выполнения различных функций: погрешности счетчиков энергии приводят к неопределенности в учете электроэнергии; погрешности весов ведут к обману покупателей или к большим объемам неучтенного товара.
Повышение точности измерений позволяет определить недостатки технологических процессов и устранить эти недостатки, что приводит к повышению качества продукции, экономии энергетических и тепловых ресурсов, сырья, материалов.
Измерения могут быть классифицированы по характеристике точности на:
Равноточные – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений и в одних и тех же условиях;
Неравноточные – ряд измерений какой-либо величины, выполненных несколькими различными по точности СИ и (или) в нескольких разных условиях.
К разным видам средств измерения предъявляют специфические требования: например, лабораторные средства должны обладать повышенной точностью и чувствительностью. Высокоточными СИ являются, например, эталоны. Эталон единицы величины – средство измерений, предназначенное для воспроизведения и хранения единицы величины, кратных или дольных ее значений с целью передачи ее размера другим средствам измерений данной величины. Эталоны являются высокоточными средствами измерений и поэтому используются для проведения метрологических измерений в качестве средств передачи информации о размере единицы. Размер единицы передается «сверху вниз» от более точных средств измерений к менее точным «по цепочке»: первичный эталон ( вторичный эталон ( рабочий эталон 0-го разряда ( рабочий эталон 1-го разряда … ( рабочее средство измерений. Метрологические свойства средств измерений – это свойства, влияющие на результат измерений и его погрешность. Показатели метрологических свойств являются их количественной характеристикой и называются метрологическими характеристиками. Все метрологические свойства средств измерений можно разделить на две группы:
Свойства, определяющие область применения СИ
Свойства, определяющие качество измерения. К таким свойствам относятся точность, сходимость и воспроизводимость.
Наиболее широко в метрологической практике используется свойство точности измерений, которое определяется погрешностью. Погрешность измерения – разность между результатом измерения и истинным значением измеряемой величины.
Точность измерений СИ – качество измерений, отражающее близость их результатов к действительному (истинному) значению измеряемой величины.
Точность определяется показателями абсолютной и относительной погрешности.
Абсолютная погрешность определяется по формуле: Хп= Хп – Х0, где: Хп – погрешность поверяемого СИ; Хп – значение той же самой величины, найденное с помощью поверяемого СИ; Х0 – значение СИ, принятое за базу для сравнения, т.е. действительное значение.
Однако в большей степени точность средств измерений характеризует относительная погрешность, т.е. выраженное в процентах отношение абсолютной погрешности к действительному значению величины, измеряемой или воспроизводимой данным СИ.
В стандартах нормируют характеристики точности, связанные и с другими погрешностями:
Систематическая погрешность – составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины. Такая погрешность может проявиться, если смещен центр тяжести СИ или СИ установлен не на горизонтальной поверхности.
Случайная погрешность – составляющая погрешности результата измерения, изменяющаяся случайным образом в серии повторных измерений одного и того же размера величины с одинаковой тщательностью. Такие погрешности не закономерны, но неизбежны и присутствуют в результатах измерения.
Погрешность измерений не должна превышать установленных пределов, которые указаны в технической документации к прибору или в стандартах на методы контроля (испытаний, измерений, анализа).
Чтобы исключить значительные погрешности, проводят регулярную поверку средств измерений, которая включает в себя совокупность операций, выполняемых органами государственной метрологической службы или другими уполномоченными органами с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям.
В повседневной производственной практике широко пользуются обобщенной характеристикой – классом точности.
Класс точности средств измерений – обобщенная характеристика, выражаемая пределами допускаемых погрешностей, а также другими характеристиками, влияющими на точность. Классы точности конкретного типа СИ устанавливают в нормативных документах. При этом для каждого класса точности устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающим уровень точности СИ данного класса. Класс точности позволяет судить о том, в каких пределах находится погрешность измерений этого класса. Это важно знать при выборе СИ в зависимости от заданной точности измерений.
Обозначение классов точности осуществляются следующим образом:
Если пределы допускаемой основной погрешности выражены в форме абсолютной погрешности СИ, то класс точности обозначается прописными буквами римского алфавита. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, присваиваются буквы, находящиеся ближе к началу алфавита.
Для СИ, пределы допускаемой основной погрешности которых принято выражать в форме относительной погрешности, обозначаются числами, которые равны этим пределам, выраженным в процентах.
Обозначения класса точности наносят на циферблаты, щитки и корпуса СИ, приводят в нормативных документах. Средствам измерений с несколькими диапазонами измерений одной и той же физической величины или предназначенным для измерений разных физических величин могут быть присвоены различные классы точности для каждого диапазона или для каждой измеряемой величины.
Классы точности присваиваются при разработке СИ по результатам приемочных испытаний. В связи с тем, что при эксплуатации их метрологические характеристики обычно ухудшаются, допускается понижать класс точности по результатам поверки.
При подготовке и проведении высокоточных измерений в метрологической практике учитывают влияние объекта измерения, субъекта, метода измерения, средства измерения, условий измерения. Так, объект должен быть всесторонне изучен; элемент субъективизма в результатах измерения должен быть сведен к минимуму; учитывают факторы и условия, которые могут искажать результаты измерений. Поэтому необходимо соблюдать методику выполнения измерений, чтобы получить результаты с минимальной погрешностью. Такие методики изложены в законе РФ «Об обеспечении единства измерений. А в 1997 году начал действовать ГОСТ 8.563-96 «ГСИ. Методики выполнения измерений».
В моей повседневной работе мне не часто приходится сталкиваться с различными средствами измерений. Однако приведу некоторые сравнительные примеры, в которых о точности можно судить по порогу чувствительности. Во многих современных продуктовых магазинах сейчас установлены электронные весы, являющиеся рабочим средством измерений. Диапазон таких весов – от 0 до 10 кг, а цена деления (если так можно выразиться для электронной версии весов) или порог чувствительности составляет 1 грамм. Таким образом, точность взвешивания достаточно высока и погрешность может составлять 0.001 кг. И не только точность измерения, но и точность расчетов с покупателями – ведь от веса продукта зависит его цена. К сожалению, класс точности не был указан на корпусе, а сотрудники при таком вопросе пришли в замешательство.
В продуктовых магазинах часто можно встретить и обыкновенные весы, на которых взвешивают с помощью гирек, которые тоже являются рабочим средством измерений. Я первый раз обратила внимание на такие весы и увидела(!), что в нашем магазине они стоят на неровной поверхности. Дело в том, что в корпус весов вмонтирован полый шарик, наполненный водой. Если весы установлены ровно, то верхняя кромка воды (под действием физических законов) располагается параллельно поверхности. В моем случае это явно было не соблюдено. Диапазон весов – от 0 до 5 кг, а порог чувствительности – 10 грамм. Из этого следует, что такие весы менее точные, нежели описанные выше – электронные, так как погрешность может составлять 0.01 кг.
У нас на работе на складе установлены весы для взвешивания овощей. Эти весы имеют диапазон от 0 до 200 кг, так что любой взрослый человек может легко на них взвеситься. Порог чувствительности составляет 200 грамм и это указано на циферблате. Помимо этого, на циферблате указано, что весы изготовлены фирмой Suprema S.p.a., диапазон 0-200 кг, e-d=200 gr, серийный номер № 122001/21 и индивидуальный номер №91097. Также там указан и класс точности – III – для подобных средств измерений, относящихся к профессиональному оборудованию. В паспорте этих весов указано, что классы точности для данной продукции установлены от I до III, вероятно, согласно нормативным документам, действующим в стране-производителе.
И, наконец, безмен, имеющий самый низкий класс точности и являющийся рабочим средством измерения. С помощью этого средства можно произвести скорее примерное взвешивание, т.к. цена деления составляет 0.5 кг и погрешность при измерении будет очень значительна. Диапазон безмена – от 0 до 7 кг. Но даже при таком неточном средстве измерения, результат зависит от некоторых факторов. В данном случае результат измерений напрямую зависел от человека, производящего измерения. При повторном взвешивании погрешность была очень высока и зависела от дрожания рук и от того, насколько точно вертикально было положение безмена. 1