Чем определяется точность эксперимента в методе вращающихся дисков
МЕТОД ВРАЩАЮЩЕГОСЯ ДИСКОВОГО ЭЛЕКТРОДА
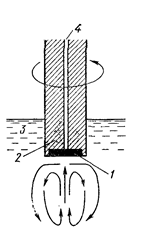
Изучение кинетики электрохимических процессов в стационарных условиях осуществляется с использованием метода вращающегося дискового электрода. Рабочей частью этого электрода служит металлический диск (платина, уголь), который впрессован в изолирующую оболочку (рис.3).
Оболочка вместе с диском приводится во вращение при помощи электромотора, причем вращение происходит вокруг оси самого электрода. Диск через металлический токоотвод поляризуется от внешнего источника тока.
При вращении электрода жидкость, соприкасающаяся с центром диска, отбрасывается к его краям, а снизу к центру электрода подходят новые потоки раствора. Согласно гидродинамической теории в этих условиях при ламинарном режиме размешивания вблизи вращающегося дискового электрода образуется граничный слой толщины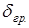 
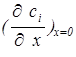
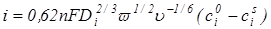
, в котором происходит монотонное изменение скорости движения жидкости относительно поверхности электрода. Чем ближе к поверхности электрода, тем меньше скорость потока жидкости относительно диска и тем большую роль в подводе реагирующих веществ и в отводе продуктов реакции играет диффузия. Таким образом, распределение концентрации реагирующих веществ у поверхности вращающегося дискового электрода обусловлено диффузией в движущейся жидкости. Функция сi(х), получающаяся в результате решения соответствующего дифференциального уравнения, не может быть представлена в аналитическом виде и обычно записывается в форме быстро сходящегося ряда. Если продифференцировать эту функцию, а затем частное значение производной 
подставить в уравнение (2), то получим формулу:
(14), где
w-угловая скорость вращения электрода,
u- кинематическая вязкость раствора,
Уравнение (14) справедливо при избытке фонового электролита, клгда можно не учитывать эффект миграции. Расчеты по формуле (14) и эксперимент согласуются до 1 %.
При больших катодных поляризациях, когда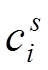 
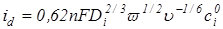
® 0, ток достигает своего предельного значения:
(15)
Разделив уравнение (14) на (15) снова получим уравнение (10), а затем уравнение поляризационной кривой (12). Таким образом, перемешивание электролита не нарушает формы поляризационной кривой в условиях лимитирующей стадии массопереноса, но значительно повышает измеряемые токи и резко сокращает время установления стационарного состояния (от часов до долей секунды).
Благодаря точному математическому описанию для плотности тока метод ВДЭ широко используется для решения разнообразных практических задач. Так зависимость предельной плотности тока от концентрации раствора используется в аналитической химии путем построения градуировочного графика.
С использованием этого метода можно определить эффективное число электронов ( n ) электрохимического процесса. Это очень важно при установлении механизма электродных реакций, особенно с участием органических соединений. При определении n обычно сравнивают предельные диффузионные токи для исследуемого вещества и для другого вещества, близкого по строению, а следовательно и по величине Di, механизм электровосстановления которого известен. Некоторые различия в значениях D не играют роли, т.к. n имеет только целочисленные значения. Если же величина n известна, то уравнение (15) может быть использовано для точного расчета коэффициента диффузии реагирующего вещества.
При помощи метода ВДЭ можно установить природу лимитирующей стадии электродного процесса. Так, если наиболее медленной стадией является стадия массопереноса, то ток прямо пропорционален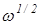 
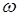
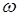
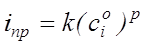
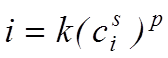
. Если же лимитирующая стадия не связана с подводом или отводом реагирующего вещества, то ток не зависит от скорости вращения. В ряде случаев при изменении 
наблюдается переход от лимитирующей стадии массопереноса к замедленной стадии разряда или к замедленной гетерогенной химической реакции. При этом по зависимости тока от можно установить порядок гетерогенной реакции р и её предельную скорость iпр. при заданном потенциале электрода. Действительно, 
,
.
Разделив уравнение (17) на (16) и подставив вместо соотношения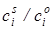 
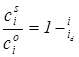
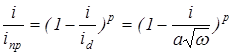
выражение (10) 
, получим:
,
где а = –0,62 nF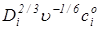
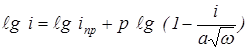
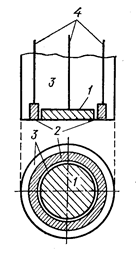
. Уравнение можно переписать в логарифмической форме:
.
В 1958 году академик А.Н.ФРУМКИН и Л.Н. НЕКРАСОВ предложили новый вариант вращающегося электрода – ВДЭсК Его рабочая часть представлена на рис.4.
Рис.4. Рабочая часть дискового электрода с кольцом в разрезе и с торца. 1-диск, 2- кольцо, 3-тефлоновая оболочка, 4- токоотвод.
Электрический диск и кольцо независимы, т.к. разделены тонкой прокладкой из изолирующего материала, а механически они представляют единое целое и вращаются вокруг единой оси. Продукты реакции, образующиеся на диске, вместе с потоком жидкости проходят мимо кольца и могут быть зафиксированы на нём при помощи измерения токов окисления или восстановления. Если продукт реакции устойчив, то отношение тока на кольце – Iк к току на диске Iд дает некоторый коэффициент N, который определяется только радиусами диска и кольца.Если же продукт реакции неустойчив, то отношение Iд/Iк
ИЗМЕРЕНИЯ
Определите взвешиванием массу пули. Установите маятник, прибор Поля и стойку для крепления ружья так, чтобы ось ствола ружья была параллельна оси двигателя и совпадала с осью цилиндра маятника. Возьмите два бумажных диска диаметром 26 см и поместите оба диска в зажимы на ось двигателя. Для этого нужно отвернуть гайку, крепящую вал, и сдвинуть вал влево. После этого зажимы для дисков легко снимаются с вала.
Насадите оба зажима с дисками на ось двигателя и закрепите их на расстоянии 15-30 см.
Пустите в ход двигатель. Когда установится постоянная скорость вращения, измерьте число оборотов двигателя в минуту с помощью электронного тахометра. Для этого включите клавишу «100», присоедините к валу мотора тахометр и нажмите кнопку, расположенную на корпусе тахометра. Держать кнопку в нажатом состоянии можно не более 5 секунд. По шкале прибора определите частоту вращения мотора. Скорость вращения также можно найти, используя паспортные данные двигателя. Тщательно определите положение указателя маятника по шкале.
Затем произведите выстрел. Пуля пробьет оба диска. Немедленно замерьте по шкале крайнее положение указателя при отклонении маятника. Остановите двигатель и определите угол поворота дисков за время полета пули между ними. Так как этот угол мал, то дугу АВ можно заменить хордой АВ.
Отметьте пробоины в дисках и повторите измерения с другими пулями. Вычислите средние скорости движения пули, определенные отдельно кинематическим и динамическим методом. Оцените погрешность измерений. Длина нити подвеса и масса маятника дается в лаборатории.
Данные измерений и расчетов оформите в таблицы.
Дополнительное задание (не обязательное для всех)
Изготовив первый (по ходу пули) диск из двойного листа бумаги, вновь определите скорость полёта пули кинематическим методом. Сравните полученное значение скорости с предыдущим и проверьте, существенно ли влияет толщина диска на результаты эксперимента. Если влияние существенно, введите необходимую поправку в найденную величину скорости пули.
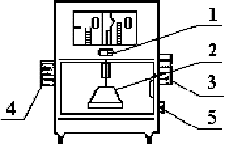
Массу пули удобно определять с помощью торсионных весов. Торсионные весы предназначены для быстрого и точного взвешивания тел малой массы. Данные весы имеют предел измерений 500 мг. Основным элементом торсионных весов является плоская спиральная пружина, которая закручивается под действием взвешиваемого предмета. Общий вид торсионных весов WT изображен на рис 4. 
Правильная установка весов проверяется по уровню 1, чашка 2 находится на конце подвижного рычага и предохранена стеклянным ограждением. Регулировочная головка 3 служит для подвода неподвижной стрелки на нулевое деление. Головка 4 используется при фактическом взвешивании, эта головка вращает барабан со шкалой, на которой отсчитываются измеренные величины. Рычаг 5 предназначен для блокировки подвижного рычага.
Правила измерения на весах.
Проверьте установку весов по уровню 1. При закрытых дверцах разблокируйте подвижный рычаг, установив красную точку 5 на нуль. Вращением головки 4 установите стрелку на красную черту, определяющую положение равновесия. Вращением головки 3 установите неподвижную стрелку на нулевое деление шкалы.
Приступая к взвешиванию, следует открыть ограждение чашки. Чашка 2 является очень точной частью и чувствительной к повреждению, поэтому будьте осторожны!
Возьмите испытуемый образец, осторожно поместите его на чашу весов. После этого закройте ограждение. Левую головку 4 вращайте от себя до тех пор, пока подвижная стрелка не достигнет красной черты равновесия. После отсчета результата, шкалу установите при помощи головки 4 в исходное (нулевое) положение. Заблокируйте весы рычагом 5, поставив красную точку на Z. Осторожно снимите взвешиваемый образец с чаши весов, закройте дверцу.
Напомним, что массу образца на торсионных весах отсчитывают в миллиграммах.
Контрольные вопросы
1. Чем определяется точность эксперимента?
2. Как зависит точность результатов от скорости пули, от скорости вращения дисков, от толщины бумаги, от расстояния между дисками? Каковы способы экспериментальной проверки влияния всех этих факторов?
3. Можно ли пользоваться выше приведенной теорией, если скорость пули имеет заметную составляющую в направлении, перпендикулярном к плоскости колебания маятника?
4. Почему неравенство t
6. Для чего подвес маятника делается бифилярным?
1. Сивухин Д.В. Общий курс физики: В 5 т. Т.1. Механика.—М.: Наука,1979.— §§ 3, 10-12, 24, 25, 26, 30, 32-35, 41.
2. Хайкин С.Э. Физические основы механики. — М.: Наука, 1971.— §§ 13, 14, 22, 26, 29-32, 67, 68, 89, 70, 71, 94, 95.
3. Стрелков С.П. Механика—М.:Наука, 1965.— §§ 16-19, 24, 25, 26, 33, 50-54, 59, 124.
4. Матвеев А.Н. Механика и теория относительности.—М.: Высшая школа, 1976. — §§ 9, 22, 24-26, 42, 44, 49, 50, 51.
5. Савельев И.В. Курс общей физики:В 3 т. Т.1.—М.: Наука, 1977.— §§ 8, 9, 18, 24, 27-29, 38, 39, 41, 53.
6. Бурсиан Э.В. Физические приборы.—М.:Просвещение, 1984.—
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Большая Энциклопедия Нефти и Газа
Метод вращающегося диска позволяет рассчитывать удельную скорость растворения, не зависящую от общего объема раствора в случае, если концентрация продукта реакции далека от насыщения. Если кинетические кривые линейны, скорость растворения вычисляют обычным способом, относя QJ г-ион к т, выраженному в секундах. [1]
Метод вращающегося диска обеспечивает хорошую воспроизводимость результатов, что не всегда достижимо при использовании других методов исследования кинетики растворения. [2]
Метод вращающегося диска был выбран потому, что он позволяет воспроизводить гидродинамический режим от опыта к опыту. Кроме того, как правило гетерогенные ] химические реакции протекают в движущихся средах, поэтому выяснение влияния критической области на кинетику гетерогенных реакций было важно провести в условиях движущейся жидкости. [6]
В случае метода вращающегося диска вместо уравнения (5.3) следует решить уравнение зависимости концентрации деполяризатора от расстояния до электрода в условиях ламинарного конвективного переноса деполяризатора к поверхности дискового электрода. [8]
Параллельно, методом вращающегося диска на модельных материалах, представляющих собой стеклоуглерод и пирографит с различной температурой обработки, квазимонокристалл, а также на искусственных графитах изучен процесс взаимодействия расплава никеля с углеродным материалом без приложения внешнего давления. [11]
Полярографический метод и метод вращающегося диска отличаются от двух других методов тем, что в них наблюдают стационарный ток, а не ток, меняющийся во времени. [12]
Полученные результаты позволяют рекомендовать метод вращающегося диска для практических целей. [14]
Методом вращающихся дисков
Определение скорости полета пули
Лабораторная работа № 7
Обработка результатов измерений
1. Рассчитайте периоды колебаний маятника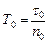 
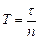
и 
, найдите их средние значения.
2. Определите абсолютные погрешности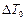 
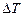
и 
методом среднего значения.
3. Вычислите момент инерции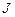 
по формуле (4) и его среднее значение.
4. Рассчитайте относительную и абсолютную погрешности по формулам:
и 
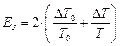
5. Конечный результат измерения момента инерции запишите в виде:
;
.
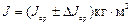
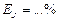
6. Сделайте вывод по проделанной работе.
Контрольные вопросы
1. В чем сущность метода определения момента инерции твердого тела?
2. Как вычислить момент инерции тела относительно произвольной оси?
3. Выведите формулу для расчета погрешностей.
Цель работы: ознакомиться с кинематическим методом определения скорости полета пули.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Методы измерения скорости света
МЕТОДЫ ИЗМЕРЕНИЯ СКОРОСТИ СВЕТА
1. Основные этапы измерения скорости света. 4
2. Методы измерения скорости света. 7
2.1 Астрономические измерения. 7
2.2 Времяпролетные эксперименты. 9
2.3 Электромагнитные постоянные. 12
2.4 Применение резонаторов. 13
2.5 Интерферометрия. 14
3. Прочие эксперименты. 15
3.1 Распространение света в среде. 15
3.2 Максимальная скорость света. 17
Список используемой литературы. 20
Скорость света является одной из фундаментальных величин и играет важную роль в физике. Она характеризует величину скорости распространения электромагнитных волн в вакууме и относится к постоянным, которые характеризуют не только отдельные тела и поля, но и геометрию пространства-времени в целом. На сегодняшний день, скорость света в вакууме является предельной скоростью движения частиц и распространения взаимодействий. Численно её значение равно 299 792,458 км/с.
В природе со скоростью света распространяются собственно видимый свет и любое другое электромагнитное излучение и, предположительно, гравитационные волны, если таковые существуют.
Массивные частицы могут иметь сколь угодно большие скорости, но всегда заведомо меньше скорости света. Такими частицами, движущимися с околосветовыми скоростями, являются, например, частицы в ускорителях или космические лучи.
Скорость света не зависит от движения источника и наблюдателя и является инвариантом во всех инерциальных системах отсчёта. Такая инвариантность постулируется в специальной теории относительности и подтверждается множеством экспериментов.
1. ОСНОВНЫЕ ЭТАПЫ ИЗМЕРЕНИЯ СКОРОСТИ СВЕТА
Античные мыслители полагали, что скорость света бесконечна, используя в качестве аргумента аналогию полёта стрелы: её траектория тем прямее, чем больше скорость. Платон был сторонником теории зрительных лучей, «ощупывающих пространство». Демокрит и Аристотель настаивали в свою очередь на истечении атомов предметов, которые проникают в зрительные органы человека. Однако, геометрическая интерпретация распространения света, разработанная в работах Евклида, практически сделала обе точки зрения эквивалентными.
Но уже в Новое время факт бесконечности скорости света ставился под сомнения такими учёными как Галилей и Гук, допускавшими, что скорость света конечна, хотя и очень велика. В это время как Кеплер, Декарт и Ферма продолжали настаивать на её бесконечности.
Декарт выдвинул идею о распространении света с бесконечной скоростью посредством давления в среде. Гук первый предложил волновую теорию света: свет есть волновое движение в однородной среде. Эта теория была развита впоследствии Гюйгенсом в его работах. Ньютон старался не высказываться про скорость света, но явно придерживался корпускулярных воззрений на счёт света.
Первая астрономическая оценка скорости света была получена в 1676 году Рёмером. Он заметил, что когда Земля и Юпитер находятся по разные стороны от Солнца затмения спутника Юпитера Ио происходят с запаздыванием в 22 мин. Отсюда было получено первая оценка скорости света – 220 000 км/c. Вскоре Брэдли, в 1728 году, используя явления аберрации света, подтвердил конечность скорости света и уточнил её значение до 308 000 км/с.
Впервые измерить скорость света в земных условиях за счёт прохождения светом известного расстояния удалось в 1849 Физо. Свет преодолевал расстояние около 9 км, а его регистрация была осуществлена с помощью «метода прерываний». Значение скорости света, полученное в ходе измерений, составило 312 000 км/с.
Несколько иной подход («метод вращающегося зеркала») был использован Фуко в 1862. Суть метода заключалась в измерении малых промежутков времени с помощью быстро вращающегося зеркала. Измерения дали значение 298 000 ± 500 км/c. Длина базы в опыте Фуко была небольшой. Впоследствии техника данного эксперимента была значительно улучшена, и уже в 1926 в эксперименте Майлькельсона погрешность была снижена до 4 км/c при измеренной величине скорости света 299 796 км/с. База при этом составляла 35 км!
Дальнейшее развитие методов измерения скорости было связано с изобретением квантовых генераторов (лазеров), дающие высоко когерентное излучение, позволившие определять скорость света одновременным измерением длины волны и частоты излучения. К началу 1970-х величина погрешности таких измерения приблизилась к 1 м/c. Так, на XV Генеральной конференции мер и весов в 1975 году скорость света в вакууме была принята равной 299 792 458 м/с с абсолютной погрешностью 1,2 м/с.
Следует отметить, что последующее повышении точности было затруднено из-за точности определения метра. Исходя из этого, на XVII Генеральной конференции мер и весов скорость света в вакууме была зафиксирована, а метр было рекомендовано определять как расстояние, которое проходит свет за 1/299 792 458 секунды.
Таблица 1. Прогресс в измерении скорости света