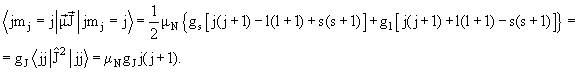Чем определяется спин ядра
Спин и магнитный момент нуклонов и ядра. Сверхтонкая структура атомных спектров
Вы будете перенаправлены на Автор24
Спин ядра
Магнитный момент нуклонов и ядра
Орбитальное перемещение протонов в ядре атома ведет к тому, что магнитный момент ядер атомов отличен от нуля. Помимо этого, нуклоны обладают собственным магнитным моментом, который связан со спином как:
Готовые работы на аналогичную тему
Ядерный магнетон Бора является естественной единицей магнитного момента ядра. Его формула совпадает с формулой для магнетона Бора ($<\mu >_B$), где масса электрона заменена на массу протона. В результате:
Сверхтонкая структура атомных спектров
Взаимодействие магнитных моментов электронов в атоме с ядром ведет к дополнительному расщеплению энергоуровней. Как результат: линии тонкой структуры дополнительно расщепляются, возникает сверхтонкая структура линий спектра. Данное расщепление весьма мало (около тысячных нм). Его наблюдают при помощи спектральных приборов, которые имеют высокую разрешающую способность.
Первые измерения спинов и магнитных моментов ядер были изначально получены при исследовании сверхтонкой структуры линий спектра. Данный метод не был точен и утратил свое значение на сегодняшний момент. Все сведения о спинах и магнитных моментах в дальнейшем получали методом ядерного магнитного резонанса.
Гипотеза Паули предполагала, что сверхтонкая структура линий спектра появляется вследствие взаимодействия магнитного момента атомного ядра с магнитным полем, которое создано электронной оболочкой (орбитальным и спиновым моментами электронов). Помимо этого ядро может обладать электрическим квадрупольным моментом, электрическими и магнитными мультиполями, которые взаимодействуют с электронной оболочкой. Данная гипотеза полностью подтверждена. Основную роль играет магнитный дипольный момент ядра. Он взаимодействует с магнитным полем электронной оболочки, которая окружает ядро. Это взаимодействие ведет к расщеплению энергетических уровней. С этим связана (в основном) сверхтонкая структура энергоуровней и линий спектра.
Отметим, что в спектральном приборе наблюдают сверхтонкая структура не энергетических уровней, а спектральных линий. Каждая линия спектра сверхтонкой структурой появляется как результат перехода атома с одного подуровня на другой. Допустимые переходы определены правилами отбора.
Интенсивности линий спектра сильно зависят от кратности вырождения энергетических уровней, между которыми идут квантовые переходы.
Решение:
\[j_1+j_2\le I\le \left|j_1-j_2\right|\left(1.1\right).\]
Так как выполняется неравенство (1.1), то:
\[\frac<5><2>+\frac<3><2>\le I\le \left|\frac<5><2>-\frac<3><2>\right|\to 4\le I\le 1\left(1.2\right).\]
Так как длина стороны треугольника не может быть больше суммы (4) или меньше разности (1), то механический момент ядра в нашем случае может иметь значения:
Задание: Какое явление получило название азотной катастрофы?
Решение:
\[14p+7e^-=21\ (частица)\ \left(2.1\right).\]
Так, измерение значений спинов ядер подтолкнуло к выводу о том, что электроны не входят в состав ядер атомов.
Получается, что спин ядра атома азота будет целым.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 06 2021
Чем определяется спин ядра
Для ядра как системы A нуклонов пространственная четность есть произведение четностей (3.1) всех нуклонов:
 A+1 = A+1 =  A + A + 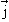 = 0 + = 0 + 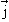 ; JA+1 = j. ; JA+1 = j. | (3.3) |
Четность основного состояния ядра с одним нуклоном сверх замкнутой оболочки или подоболочки определена четностью (-1) l неспаренного нуклона. Поскольку
Рассмотрим теперь ядра, у которых до заполненной оболочки или подоболочки недостает одного нуклона. Эти ядра часто называют ядрами с одной “дыркой” (hole) относительно замкнутой подоболочки или оболочки. У всех таких ядер спин и четность определяются моментом и четностью “отсутствующего” нуклона, т.е. моментом и четностью “дырки”. Действительно,
 A-1 + A-1 + 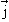 h = h =  A = 0; JA+1 = jh. A = 0; JA+1 = jh. | (3.5) |
Здесь момент недостающего нуклона обозначен как jh, где h соответствует обозначению “hole”. Аналогично (3.4) получим для четности ядра с одной “дыркой”
| Пример 2. Определить спины и четности основных состояний ядер 3 He и 11 B. |
| Пример 3. Определить спин и четность основного состояния ядра 7 Li. |
| Пример 4. Найти спин и четность ядра 26 Al в основном состоянии и сравнить результат с экспериментальным. |
Ядро 26 Al в основном состоянии соответствует протонной и нейтронной «дыркам» относительно ядра 28 Si:
Если при возбуждении ядра, т.е. при поглощении ядром некоторой энергии, эта энергия передается одному нуклону над замкнутой оболочкой или подоболочкой, этот неспаренный нуклон будет переходить на более высокие уровни энергии, а остальные нуклоны ядра (т.н. кор) будут оставаться в прежних невозбужденных состояниях. Такие возбуждения называются одночастичными. В спектрах возбуждения ядер с одним нуклоном над замкнутой оболочкой или подоболочкой можно выделить уровни, соответствующие одночастичным возбуждениям. (См., например, задачу о возбужденных состояниях ядра 17 О). Однако вид спектра возбужденных состояний ядра 17 О показывает, что только часть наблюдаемых уровней имеет одночастичную природу. Другие возбужденные состояния этого же ядра представляют собой результат переходов нуклонов из «кора» (т.е. ядра 16 О) и имеют более сложную структуру.
Рассмотрим возбуждения ядер с замкнутыми оболочками или подоболочками, например, ядра 12 С. Конфигурация его основного состояния может быть представлена как
Возбужденные состояния этого ядра могут возникнуть в результате перехода одного из нуклонов 1р3/2 на более высокую подоболочку 1р1/2. Этому состоянию будет соответствовать конфигурация
Представление возбужденных состояний систем на языке «частично – дырочных конфигураций» (particle-hole configurations) широко используется в теории квантовых систем многих частиц.
| Задача 3.1. В спектре возбужденных состояний ядра 17 О (рис.3.1) указать уровни, соответствующие одночастичным возбуждениям. |
 Рис.3.1. |
Основное состояние 17 О соответствует одному нейтрону над замкнутой оболочкой: Переходы неспаренного нейтрона с подоболочки 1d5/2 на более высокие подоболочки 2s1/2 и 1d3/2 соответствуют возбужденным состояниям 1/2 + и 3/2 + в спектре 17 O. Разность энергий 3/2 + и 5/2 + уровней в спектре 17 О является следствием спин-орбитального расщепления.
| Задача 3.2. Оценить константу а в потенциале спин-орбитального взаимодействия из этой разности энергий уровней 3/2+ и 5/2+ уровней в спектре 17 О. |
| Задача 3.3. Определить (в ОМО) спины и четности возбужденных состояний ядра 12 С, которые возникают в результате перехода нуклона из замкнутой подоболочки 1р3/2 в следующую 1р1/2 подоболочку. |
В данной задаче удобно принять основное состояние ядра 12 С за физический вакуум: тогда переход нуклона в следующую подоболочку эквивалентен рождению частично- дырочной пары над вакуумным состоянием. Спин такого возбужденного состояния равен векторной сумме моментов частицы и “дырки”:
| Задача 3.4. Определить спин и четность низшего по энергии частично-дырочного возбужденного состояния ядра 16 O. По экспериментальному спектру энергий возбуждения указать энергию этого состояния. |
Принимая основное состояние 16 O за физический вакуум, имеем для возбужденного состояния, возникающего вследствие перехода нуклона из 1р1/2 в следующую подоболочку 1d5/2:
Изоспин ядер в основных и возбужденных состояниях
В лекции 1 было показано, что низшим по энергии состояниям системы нуклонов, т.е. основным состоянием ядра, является состояние с низшим возможным значением изоспина, которое равно величине модуля проекции изоспина
Рассмотрим изоспины возбужденных состояний ядер. Для частично-дырочных возбуждений возможны два значения изоспина возникающего возбужденного состояния, соответствующие двум значениям векторной суммы изоспинов квазичастиц: Низшим по энергии возбуждения оказываются состояния с изоспином 0. Инвариантность сильных взаимодействий относительно вращений в изоспиновом пространстве ярко проявляется в подобии спектров т.н. зеркальных ядер (“mirror nuclei”). (См., например, рис. 3.2). У этих ядер одинаковые числа нуклонов и тождественные значения изоспина. Поскольку число нейтронов одного равно числу протонов другого, эти ядра имеют противоположные по знаку величины проекций изоспина.
Остаточные взаимодействия между квазичастицами зависят от изоспина. Состояния с более высокой энергий возбуждения могут иметь изоспин 1, причем проекция изоспина остается равной проекции изоспина для основного состояния ядра – она определена числом протонов и нейтронов данного ядра.
| Задача 3.5. Каковы возможные значения спина, четности и изоспина возбужденного состояния ядра 12 С (3.10)? |
Магнитный дипольный момент ядер в ОМО
Теоретическая оценка магнитного дипольного момента атомных ядер основана на соотношении между квантовыми векторами магнитного и механического моментов:
Коэффициент gN называется ядерным гиромагнитным отношением. Его теоретическая величина может быть получена из (3.14 ) путем расчета матричных элементов левой и правой части равенства для ядерного состояния с моментом j и проекцией момента +j.
Для этой цели применим волновые функции ядер, полученные нами в рамках одночастичной модели оболочек (ОМО). В этой модели волновая функция ядра с одной частицей или одной дыркой сверх замкнутой оболочки или подоболочки определяется волновой функцией этой неспаренной квазичастицы а спин ядра определяется полным угловым моментом этой квазичастицы. (Обычно не указывают в дираковских скобках значения орбитального момента и спина квазичастицы – их сохранение подразумевается)
поскольку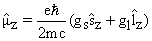
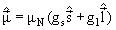
произведение векторов в (3.15) сводится к произведениям векторов полного, орбитального и спинового моментов:
Используя очевидные формулы 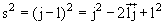
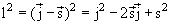
Эти теоретические результаты могут быть изображены в виде т.н. линий Шмидта для неспаренных протонов и нейтронов с полными моментами и
Экспериментальные значения магнитных моментов ядер лишь для нескольких ядер близки к линиям Шмидта, они разбросаны между кривыми для и Этот факт указывает на приближенный характер предсказаний одночастичной модели оболочек.
Модель оболочек для средних и тяжелых ядер. Роль кулоновского взаимодействия
Во всех предыдущих расчетах и комментариях не был учтен тот факт, что на протоны ядра помимо сильного взаимодействия (которое было приближенно учтено введением самосогласованного потенциала со спин-орбитальным членом), действует также кулоновское отталкивание со стороны других протонов ядра. Роль этого члена во взаимодействии была сравнительно невелика для легких ядер, но для средних и тяжелых ядер влияние кулоновского потенциала влияет на ход заполнения подоболочек и оболочек. Иными словами, если нейтроны ядра можно считать находящимися в потенциале (2.9), то для протонов в это выражение должен быть добавлен член, характеризующий кулоновское отталкивание протонов:
Спин ядра



Спин, магнитный и электрический моменты ядер
Ядро, как пространственно ограниченная и связанная система взаимодействующих между собой нуклонов, в определенных случаях может рассматриваться в целом как одна микрочастица. Так как нуклоны, из которых состоит ядро, обладают собственным механическим моментом, или спином, а также совершают движение относительно друг друга (орбитальное движение относительно центра инерции ядра), то и ядра должны иметь собственный механический момент (далее просто момент) или спин.
Спин ядра 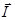
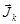
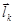
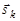
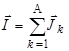 , а , а 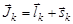 . .  | (1.6.1) |
Возможна другая схема сложения моментов отдельных нуклонов, дающая другой результат, когда сначала отдельно суммируются векторы спинов, а затем векторы орбитальных моментов всех нуклонов, и полученные два вектора складываются. Однако, поскольку ядерные силы не центральны (см. §1.9 п.7) и в ядре существует спин-орбитальное взаимодействие (см. §2.3 п.1), то по этой причине в теории ядра используют первую схему.
Вектор момента любых микрочастиц, как, впрочем, и спин ядра, обладает своеобразными свойствами.
1. Абсолютная величина вектора момента любой изолированной физической величины может принимать только дискретные значения:
|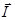 | | 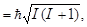 | (1.6.2) |
где I – положительное число, либо целое, либо полуцелое:
Число I называют обычно величиной момента или квантовым числом момента. Следует особо отметить различие между модулем вектора 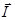
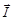
2. Мгновенное значение вектора механического момента микрочастицы не имеет смысла по той же причине, по которой в квантовой механике не имеет смысла мгновенное значение вектора импульса. Строго фиксированное значение может иметь только абсолютная величина вектора момента (1.6.2) и одна из его пространственных проекций, обычно называемой проекцией на ось Z, которая обозначается как Iz. Проекция момента Iz может принимать случайным образом одно из (2I + 1) значений, уменьшающихся на единицу:
Реализация любой возможной проекции из набора (1.6.4) оказывается равновероятной.
Число возможных проекций на ось Z четно, если I – полуцелое число, и нечетно, если I – целое число. Знак плюс или минус в (1.6.4) означает ориентацию вектора момента на выбранное направление оси Z в пространстве. Однако величины проекций Ix и Iy оказываются совершенно неопределенными[1] и флуктуируют относительно нулевого среднего значения. Учитывая, что
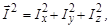 | (1.6.5) |
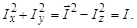 | (1.6.6) |
Таким образом, квадраты проекций вектора момента на оси Х и Y не равны нулю. По этой причине проекция момента Iz всегда меньше абсолютной величины вектора механического момента. Действительно, согласно (1.6.4), максимальное значение 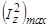
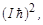
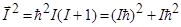
 |
Все перечисленные выше свойства вектора механического момента обычно демонстрируют с помощью квазиклассической модели (рис. 1.6.1), которая находится в определенном согласии со свойствами квантовомеханического вектора момента. Вектор момента, величина которого вычисляется с помощью (1.6.2), прецессирует относительно оси Z с некоторой угловой скоростью и может ориентироваться вдоль или против направления оси Z только таким образом, чтобы его проекция на ось Z была равна одному из значений от +Iћ до –Iћ через единицу. Этот вектор никогда не может ориентироваться точно по направлению оси Z, поскольку его величина, как отмечено выше, не равна Iћ. Поэтому, помимо величины вектора момента, сохраняющейся во времени величиной является только одна проекция вектора – проекция на ось Z. Полное число проекций Iz вектора момента на рис.1.6.1 равно (2I + 1).
3. Модуль вектора момента 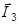
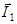
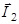
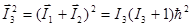  | (1.6.7) |
обычным образом через свои квантовые числа 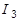
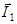
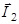
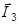
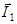
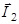
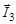
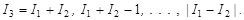  | (1.6.8) |
Соотношение (1.6.8) называется правилом сложения моментов в квантовой механике.
Поскольку каждое значение проекции из (2I1 + 1)(2I2 + 1) возможных реализуется с равной вероятностью, то относительная вероятность образования состояния со спином 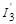
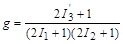 , ,  | (1.6.9) |
т.е. равна отношению числа возможных проекций вектора 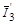
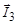
4. Любая векторная величина 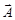
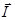
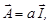  | (1.6.10) |
где а – константа, полностью характеризующая вектор.
В отношении спинов различных ядер наблюдаются следующие опытные закономерности:
а) Для ядер с четными А спины всегда целые, а при нечетном А – всегда полуцелые.
г) Ядра с нечетным А имеют полуцелый спин в пределах от 1/2 до 9/2, что крайне мало по сравнению с суммой абсоютных значений полных моментов