Чем определяется собственная частота колебаний системы

Как определить собственную частоту колебаний

Вы будете перенаправлены на Автор24

Собственные колебания

Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.

В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.

В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.

Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.

По характеру взаимодействия с окружающей средой колебания разделяют на:

В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.

При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.

В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.

Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.

Готовые работы на аналогичную тему

В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).

Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.

В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.

Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.

Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:

Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ

Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.

Колебания в нелинейных системах

Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.

Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).

Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.

Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.

Источник

Как определить собственную частоту колебаний

Для лучшего понимания вопроса рассмотрим, что собой представляют собственные колебания и колебания в нелинейных системах.

Собственные колебания

Колебания очень схожи по природе с волнами, они подчиняются общим закономерностям, единственное их отличие в том, что в процессе распространения волн энергия не переходит из одной формы в другую, а всего лишь переносится. Исследованием закономерностей физической природы волн и колебаний занимается теория колебаний и волн. На практике в реальных условиях без воздействия внешних факторов любые колебания со временем затухают, это связано с потерей энергии.

Колебания, по характеру взаимодействия с внешней средой, разделают на:

Рассмотрим подробнее собственные колебания.

Причиной возникновения таких колебаний является отклонение от равновесия одного или нескольких параметров системы. Такие колебания возникают под воздействием внутренних сил после выведения системы из равновесия.

Рассмотрим принцип суперпозиции, который гласит о том, что допустимое движение системы равно сумме ее произвольных движений. При незначительных отклонениях характеристик системы от положения равновесия, ее движение будет соответствовать принципу суперпозиции. Подобные движения описываются дифференциальными уравнениями линейного характера. Если рассмотреть консервативную систему, т.е. такую, в которой отсутствуют потери энергии и ее параметры постоянны во времени, то любое свободное колебание такой системы представляет собой сумму простых колебаний, меняющихся во времени с определенными частотами свободных колебаний по закону синуса.

Не нашли что искали?

Просто напиши и мы поможем

Системы бывают с одной или несколькими степенями свободы. Если состояние системы в любой конкретный момент времени описывается одним параметром, то такая система имеет одну степень свободы, если двумя – то две, тремя – три, и так далее. Как пример системы с одной степенью свободы, можно рассмотреть маятник, который совершает колебательные движения в плоскости. В этом случае любое конкретное его положение характеризуется углом его отклонения от оси вертикали. Для описания колебательной системы с двумя степенями свободы нужны два переменных параметра. Примером таких колебаний является маятник, колеблющийся в сфере. В этом случае переменными параметрами будут являться углы положения маятника относительно двух перпендикулярных плоскостей. Но зачастую движения системы с двумя степенями свободы имеют сложный негармоничный характер. Они описываются линейными уравнениями суперпозиций двух простых переменных параметров, которые происходят одновременно. Так вот, каждое из этих двух простых элементарных колебаний называют собственной или свободной, так называемой гармоникой.

Для колебательных систем, состоящих из определенного количества осцилляторов (к примеру вереница шариков, соединенных между собой маленькими пружинками), число гармоник будет равняться их числу. Для более сложных систем, таких как мембрана, например, гармоники будут различные по длине волн и их будет бесконечное множество. При заданной скорости распространения таких волн, спектр собственных частот определяется простой линейной формулой. При наличии волн с разной скоростью распространения такой линейный закон уже не действует, здесь в силу вступают различные дисперсионные уравнения.

Если рассмотреть реальные существующие системы, в которых собственные колебания затухают со временем, то их считают лишь относительно гармоничными в небольшом конкретном отрезке времени. Свободные колебания, затухающие во времени, могут состоять из нескольких гармоник в определенном диапазоне частот. В таком случае имеет место так называемая добротность, то есть расширение спектральной линии, которое равно отношению запасенной энергии к потерям системы. Соответственно, сгущение спектра за счет потерь влечет за собой трансформацию его дискретной формы в сплошную в том случае, если ширина линий приближается к ширине между ними.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Колебания в нелинейных системах

Свободные или собственные колебания в нелинейных системах сложно поделить на какие-либо классы. В нелинейных системах спектр частоты свободных колебаний дискретен, что приводит к движению энергии по различным компонентам спектра. В таких колебательных системах наблюдается явление конкуренции гармоник, т.е. выживание одних за счет подавления других. Лишь дисперсия может уравновесить подобный процесс, приводя к образованию устойчивых в пространстве и времени форм колебаний.

В колебательных системах частым явлением, имеющим большое значение, является процесс резонанса. Его суть заключается в резком возрастании амплитуды колебаний. Это происходит из-за приближения частоты внешнего воздействия к частоте колебания внутреннего собственного параметра системы.

Если линейная система и ее параметры находятся вне времени, то частота резонанса совпадает с частотой ее собственных колебаний. Амплитуда колебаний системы будет усиливаться с ростом параметра ее добротности. В таком случае раскачка амплитуды будет происходить до того момента, пока поступающая энергия будет больше потерь при осцилляции.

Если говорить о линейных колебаниях, то поступающая внешняя энергия пропорциональна амплитуде, а потери пропорциональны амплитуде в квадрате. Таким образом можно сказать, что баланс энергии достигается во всех известных случаях.

Источник

Определение собственных частот колебаний системы

Большинство конструкций совершают механические колеба­ния. При эксплуатации все машины, транспортные средства и здания подвергаются воздействию динамических сил, ко­торые приводят к возникновению механических колебаний [10, 17]. Очень часто необходимо провести исследование механиче­ских колебаний вследствие возникших проблем или вслед­ствие необходимости подгонки характеристик конструкции под «стандартные» или контрольные значения. Независимо от причин, необходимо получить каким-либо образом коли­чественные данные о реакции конструкции для того, чтобы можно было оценить ее влияние на эксплуатационные хара­ктеристики и усталость материалов.

Измерения и частотный анализ механических колебаний ра­ботающей конструкции могут быть выполнены с использо­ванием методов анализа сигналов. После этого может быть проведена проверка соответствия частотного спектра меха­нических колебаний заданным параметрам. Результат будет представлять произведение реакции конструкции и спектра неизвестной силы возбуждения. Он будет давать мало или не давать вообще информации о характеристиках самой кон­струкции.

Другим подходом является метод анализа систем, при кото­ром для измерения отношения реакции к замеряемой силе возбуждения может быть использован двухканальный ана­лизатор, выполняющий быстрое преобразование Фурье. Оп­ределяемые частотные характеристики способствуют выде­лению спектров силы из результатов и описанию соб­ственно свойств конструкции между точками замера. По набору замеренных в различных точках конструкции частот­ных характеристик можно начать строить картину ее дина­мического поведения. Используемый при этом метод назы­вается анализом мод колебаний. Все конструкции проявляют модальные свойства.

Определяемые экспериментальным путем частотные характе­ристики механических конструкций указывают на присутст­вие серий пиков. Отдельные пики часто очень острые и четко определенные при дискретных частотах, что указывает на резонансы, каждый из которых представляет собой хара­ктеристику системы с одной степенью свободы. Если в ре­зультате определения частотных характеристик с повышен­ным разрешением по частоте выявляются новые пики, то можно предполагать присутствие нескольких резонансов. Вследствие этого конструкция представляет собой как бы на­бор отдельных механических систем с одной степенью сво­боды. Это является основой анализа мод колебаний, с помо­щью которого может быть проведен анализ поведения кон­струкции путем определения и оценки всех резонансных частот или мод, имеющихся в характеристиках конструкции.

Рассмотрим сначала вопрос о том, как реакция конструкции может быть представлена в различных областях. Таким образом, мы сможем увидеть, как модальное описание связано с описанием в пространственной, временной и частотной областях.

В качестве примера рассмотрим реакцию колокола (рис. 2.6), который представляет собой механическую систему с малым затуха­нием. При ударе по колоколу он выдает акустическую реакцию, содержащую ограниченное число чистых тонов.

Рис. 2.6. Реакция колокола, соответствующая механическим колебаниям

Реакция, соответствующая механическим колебаниям, имеет точно такую же структуру, а колокол как бы накапливает энергию удара и рассеивает ее в виде механических колеба­ний с несколькими дискретными частотами.

На рис. 2.6 в отдельных колонках показаны реакции коло­кола, представленные в различных областях:

· в физической области сложная геометрическая деформация колокола может быть представлена с помощью набора простых независимых графиков деформации или форм мод;

· во временной области реакция в виде механических (или акустических) колебаний является временной функцией, ко­торая может быть представлена как набор затухающих синусоид:

· в частотной области анализ временного сигнала дает спектр, содержащий серию пиков, соответствующих спек­трам реакций систем с одной степенью свободы;

· в модальной области реакция колокола представлена в виде модальной модели, построенной на основе набора моделей систем с одной степенью свободы.

Так как форма моды представляет собой перемещение всех точек конструкции при соответствующей модальной частоте, то одиночная мо­дальная координата может быть использована для пред­ставления всего вклада этой моды в общую деформацию конструкции в целом. Возвращаясь к рис. 2.6, видно, что каж­дая модель системы с одной степенью свободы связана с частотой, затуханием и формой моды колебаний.

Таким об­разом, имеются следующие модальные параметры: модальная частота, модальное затухание, форма моды.

Эти параметры совместно образуют полное описание собст­венных динамических характеристик колокола и являются неизменными, независимо от того, звонит ли колокол или нет.

Анализ мод колебаний представляет собой процесс определе­ния модальных параметров конструкции для всех мод в оп­ределенном частотном диапазоне. Основной целью его про­ведения является использование этих параметров для построения математической модальной модели реакции конструкции. Построение данной модели позволяет осуществлять контроль технического состояния конструкции, т.е. выявление всевозможных дефектов (раковины, трещины, ослабление в структуре материала и др.) в конструкции и определение возможности ее дальнейшей эксплуатации.

Заслуживают внимания два обстоятельства:

1) любая вынужденная динамическая деформация конструк­ции может быть представлена в виде взвешенной суммы форм мод ее колебаний;

2) каждая мода может быть представлена в виде модели си­стемы с одной степенью свободы.

2.2.2.1. Модели систем с одной степенью свободы

Так как каждый пик (или мода) характеристики конструк­ции может быть представлен при помощи модели системы с одной степенью свободы, мы рассмотрим некоторые ас­пекты динамики систем с одной степенью свободы. В част­ности, мы исследуем методы построения моделей системы с одной степенью свободы в физической, временной и частот­ной областях. Эти модели не предназначены для представле­ния физических конструкций, но они служат в качестве инструмента для интерпретации их динамического пове­дения (представленного с помощью набора предположений и граничных условий). Модели оказываются полезными:

· для понимания и интерпретации динамического поведения конструкции;

· для описания динамических свойств конструкции с помощью небольшого набора параметров;

· для определения динамических параметров на основе экспе­риментальных результатов (подбор кривой).

Аналитическая модель может быть построена в физиче­ской области. Она представляет собой абстрактную систему, состоящую из точечной массы (m), опирающуюся на безы­нерционную линейную пружину (k) и связанную с вязкост­ным демпфером (с). Масса установлена таким образом, что она может перемещаться только в одном направлении (х), т.е. система имеет одну степень свободы.

Математическая модель во временной области может быть получена путем приложения второго закона Ньютона к аналитической модели. Приравнивая внутренние силы (инерции, затухания и упругости) и внешние силы (возбу­ждения), мы получим следующую модель:

Эта модель представлена в виде дифференциального уравне­ния второго порядка. Более простая в математическом отно­шении модель может быть получена в частотной области.

2.2.2.2. Модели систем с одной степенью свободы в частотной области

Модель с пространственными параметрами может быть построена в частотной области для описания частотной ха­рактеристики Н(ω) в терминах массы, жесткости и коэффи­циента затухания.

Рассмотрим поведение этой модели под воздейст­вием синусоидального возбуждения и проследим за измене­ниями модуля |Н(ω)| и фазы Н(ω) при изменении часто­ты.

Статическое смещение определяется только жесткостью пру­жины. При низких частотах реакция, определяемая в основ­ном пружиной, находится в фазе с силой возбуждения.

При увеличении частоты присущая массе сила инерции оказывает возрастающее влияние. При определенной частоте ( — собственная частота незатухающих колебаний) соответствующие массе и пружине составляющие взаимно аннулируются и реакция определяется только присущей демпферу составляющей. Следовательно, податливость си­стемы увеличивается. Если присущая демпферу составля­ющая была бы равна нулю, то податливость стала бы беско­нечной. При частоте реакция отстает от силы возбуждения на 90°.

При частотах, превышающих , основное влияние оказы­вает присущая массе составляющая и система начинает вести себя как чистая масса, податливость уменьшается, а реакция отстает от силы возбуждения на 180°.

Модель частотной характеристики является беспараметрической. Она основана на определяющем Н(ω) выражении, т.е.

. (2.21)

Функция Н(ω) является частотной характеристикой податли­вости (перемещение/сила). Она представляет собой отноше­ние выходного и входного спектров и изменяется в зависи­мости от частоты (ω).

Эта модель связывает аналитическую модель системы с од­ной степенью свободы с практическими измерениями и их результатами.

Рис. 2.7. Модель с пространственными параметрами

Модель с пространственными параметрами (рис. 2.7) является идеаль­ной для работы с аналитическими системами. Обычно нам неизвестны распределения массы, жесткости и затухания реальных конструкций. Следующая модель представляет со­бой практическую связь между теорией и практикой.

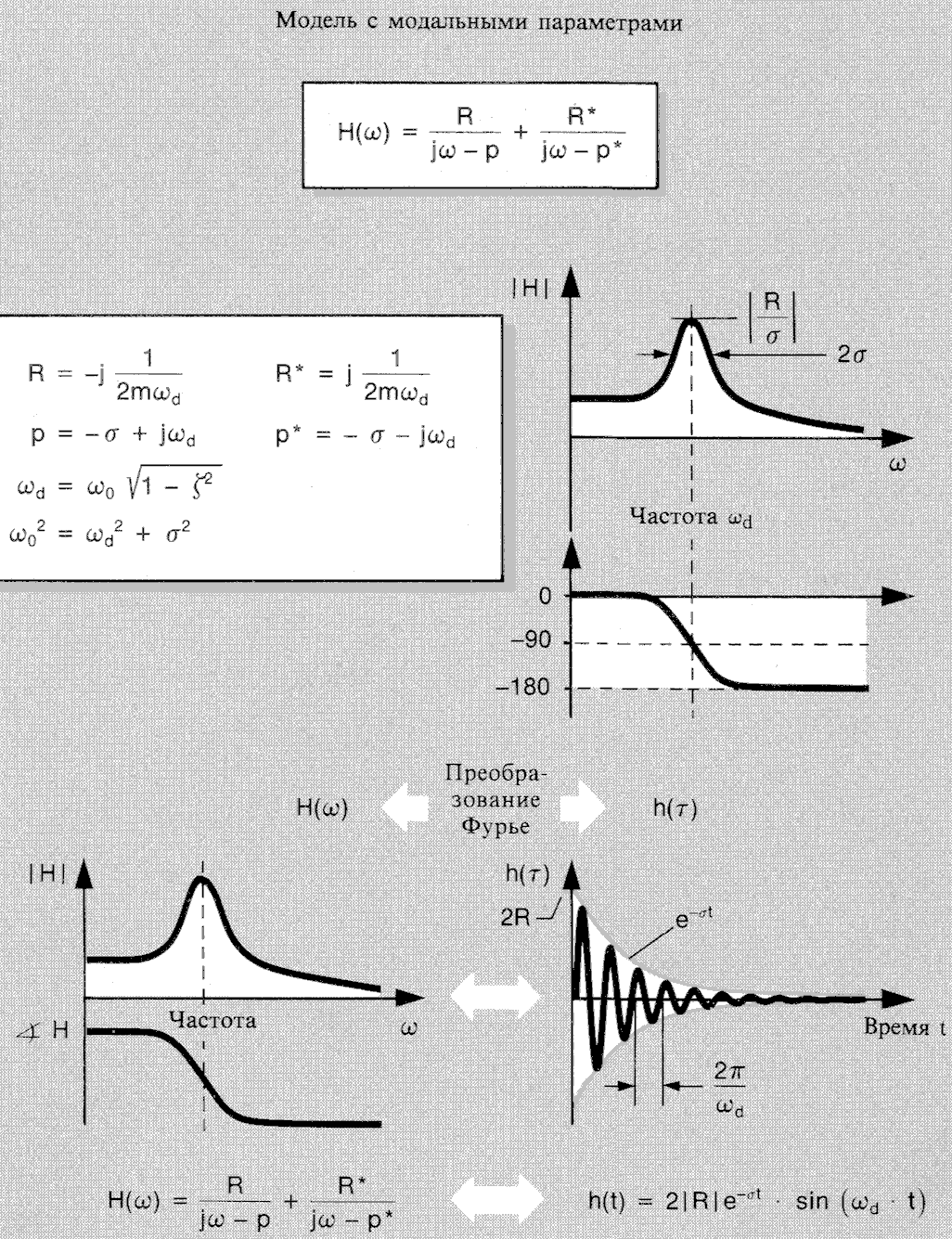
Модель с модальными параметрами показана на рис. 2.8. Она построена с помощью двух параметров, которые могут быть получены по результатам измерения частотных хара­ктеристик.

На рис. 2.8 функция Н(ω) определяется координатой полюса (р) и вычетом (R) и их комплексно сопряженными величинами (р* и R*). Координата полюса и вычет в свою очередь определяются через пространственные параметры.

Координата полюса — комплексная величи­на. Численное значение ее действительной части (σ) пред­ставляет собой скорость затухания колебаний. Это показано на графике зависимости импульсной характеристики от вре­мени. В частотной области она представляет собой половину ширины полосы (-3 дБ) пика частотной характеристики. Мнимая часть координаты полюса —мо­дальная частота, т.е. собственная частота свободно затуха­ющих колебаний (ωd).

Рис. 2.8. Модель с модальными параметрами

Вычет в случае системы с одной степенью свободы — мнимая величина, которая отображает ин­тенсивность моды колебаний.

Как показано на рис. 2.8, координата полюса и вычет могут быть определены экспериментальным путем на основе измеренной и из­ображаемой на экране анализатора частотной характеристи­ки. Таким образом, модель с модальными параметрами дает связь аналитических моделей с результатами эксперимен­тальных исследований.

2.2.2.3. Координата полюса и вычет

Так как координата полюса и вычет являются основой анализа мод колебаний, рассмотрим эти два параметра более подробно.

Вычет представляет собой математическое понятие и не имеет прямой интерпретации в физических терминах. Он со­держит абсолютный масштаб частотной характеристики и за счет этого и информацию об уровне кривой модуля. Позднее мы увидим, что вычет связан с третьим модальным параметром, т.е. с формой моды.

Вычет иногда называют напряженностью полюса, но ампли­туда моды определяется не только вычетом. Она представля­ет собой отношение вычета и скорости затухания, т.е. .

2.2.2.4. Степени свободы и модели систем с несколькими степенями свободы

Предыдущие модели относились к случаю одной степени свободы, т.е. к перемещению в одном направлении. Реаль­ные конструкции имеют много точек, которые могут переме­щаться независимо друг от друга, т.е. они являются систе­мами с несколькими степенями свободы. Для определения частотной характеристики реальной конструкции необходи­мо определить силу возбуждения и реакцию в двух точках. Однако каждая точка может перемещаться максимально в шести возможных направлениях, и поэтому необходимо так­же определить направление ее перемещений.

Степень свободы (СС) представляет собой определенную точку и направление ее перемещения. Индекс i используется для указания степени свободы реакции, а индекс j — для сте­пени свободы возбуждения. Дополнительные индексы х, у и z могут быть использованы для указания направления. Таким образом

(2.22)

Написав функцию двумя способами, можно получить две модели систем с несколькими степенями свободы. Эти модели описаны уравнениями на рис. 2.9.

Модель системы с несколькими степенями свободы, осно­ванная на частотных характеристиках, представляет фун­кцию как сумму частотных характеристик систем с одной степенью свободы, по одной функции для каждой моды в пределах учитываемого частотного диапазона, при­чем r — порядковый номер моды, m— число мод в модели.

Рис.2.9. Модели с несколькими степенями свободы.

Модель системы с несколькими степенями свободы, ос­нованная на модальных параметрах, определяет функцию в терминах координат полюсов и присущих отдель­ным модам вычетов. Эта модель указывает на три важных свойства модальных параметров:

1) модальная частота и затухание являются глобальными параметрами;

2) координата полюса имеет только модаль­ный номер (r) и не зависит от учитываемой степени свободы;

3) вычет является локальным параметром. Индексы (ij) свя­зывает вычет с конкретной комбинацией степеней свобо­ды и конкретной модой.

2.2.2.5. Определение понятия форма мод колебаний

Форма мод представляет собой, как уже было показано в примере с колоколом (см. рис. 2.6), деформацию, связанную с конкретной модальной частотой или с координатой полюса. Ее трудно наблюдать, можно только представить или смоделировать на маложестких конструкциях. При моделировании формы деформации моду колебаний можно рассматривать как абстрактный математический параметр, как если бы эта мода существовала отдельно от всех остальных мод колебаний конструкции.

Истинное физическое перемещение в любой точке всегда является комбинацией всех мод колебаний конструкции. При гармоническом возбуждении, близком к модальной ча­стоте, 95 % перемещений может быть связано с соответству­ющей конкретной формой мод, а при случайном возбужде­нии имеется тенденция к произвольной комбинации всех форм мод.

В любом случае форма мод представляет собой внутреннее динамическое свойство совершающей «свободные» механиче­ские колебания (без воздействия внешних сил) конструкции. Она отображает относительное перемещение всех частей конструкции для конкретной моды.

Формы мод являются непрерывными функциями, которые при анализе выделяются с «пространственным разрешени­ем», зависящим от числа учитываемых степеней свободы. В общем случае они не замеряются непосредственно, а опреде­ляются по набору присущих заданным степеням свободы ча­стотных характеристик. Выделенная форма мод представляется с помощью вектора формы мод <ψ>_r, где r— номер моды.

Составляющие ψ_ir вектора формы мод представляют собой относительные перемещения, присущие отдельным степеням свободы (i). Обычно они являются комплексными числами, отображающими как амплитуду, так и фазу перемещения и носит название модального перемещения.

Моды колебаний могут быть подразделены на два класса.

Нормальные моды характерны тем, что все части конструк­ции перемещаются в фазе или в противофазе (со сдвигом 180)° по отношении друг к другу. Поэтому модальные пере­мещения ψ_ir представляют собой действительные величины, принимающие положительные или отрицательные значения. Нормальные моды можно рассматривать как стоячие волны с неподвижными узловыми линиями (рис. 2.9).

Комплексные моды могут иметь какое угодно соотношение между фазами в различных частях конструкции. Модальные перемещения ψ_ir представляют собой комплексные величины, и они могут иметь любое значение фазы. Формы комплекс­ных мод могут рассматриваться как распространяющиеся волны без стационарных узловых линий (рис. 2.10).

Распределение затухания в конструкции определяет наличие нормальных или комплексных мод. Когда конструкция име­ет очень малое затухание или затухание вообще отсутству­ет, моды будут нормальными. Если затухание распределено так же, что и инерция и жесткость (пропорциональное зату­хание), можно ожидать наличие нормальных мод.

Конструкции с локализованным затуханием, такие как ку­зова автомобилей, с точечной сваркой и амортизаторами, имеют комплексные моды.

Формы мод, определенные по небольшому количеству замеров, могут указывать на комплексные моды в конструкциях, в которых имеются лишь нормальные моды.

Рис.2.9. Нормальная мода Рис.2.10. Комплексная мода

Связь вычетов и форм мод при модальной частоте (ω_dr) мо­дуль частотной характеристики определяется выражением

, (2.22)

Можно показать, что присущий конкретной моде (r) вычет пропорционален произведению модальных перемещений ψ_ir (соответствует степени свободы реакции) и ψ_jr (соответству­ет степени свободы силы возбуждения):

. (2.24)

Модальная связь представляет собой общее понятие, указы­вающее на то, насколько сильно на реакцию при одной мо­дальной частоте оказывают влияния другие моды колеба­ний. Эту связь можно наблюдать на построенной кривой частотной характеристики вблизи модальной частоты.

Моды колебаний конструкции со слабым затуханием четко отделены друг от друга, другими словами они слабо связаны. Такие системы ведут себя как системы с одной сте­пенью свободы вблизи модальных частот, а соответству­ющие конструкции получили названия простых.

При исследованиях подобных конструкций простые методы дают достоверные результаты. Простые конструкции часто встречаются при проведении поиска неисправностей, так как в большинстве случаев проблемы с шумом, механическими колебаниями и усталостью связаны с мало демпфированны­ми резонансами.

Частотные характеристики конструкций с сильным затуха­нием или высокой модальной плотностью не указывают на четко разделенные моды. При этом говорят, что моды сильно связаны, а реакция при любой частоте представляет собой комбинацию многих мод. Сложные конструкции мо­гут быть все-таки описаны с помощью дискретного набора мод, но методы, необходимые для определения модальных параметров, более сложные.

При рассмотрении понятия высо­кой модальной плотности и сильного затухания надо понимать, что ни один из этих двух факторов не мешает применению к кон­струкции модального описания. Они только усложняют ис­пользуемые методы.

Необходимо предположить, что исследуемые системы имеют линейные свойства, т.е. что реакция всегда пропорциональна силе возбуждения. Это предположение имеет три следствия для измерений частотных характеристик.

1) Наложение — измеряемые частотные характеристики не зависят от типа и формы волны возбуждения. Возбужде­ние синусоидальной силой с разверткой частоты дает те же результаты, что и возбуждение широкополосной слу­чайной силой.

2) Однородность — измеряемые частотные характеристики не зависят от уровня возбуждения.

3) Взаимность — в линейной механической системе существу­ет частная симметрия, которая описывается теоремой взаимности Максвелла. Отсюда следует, что измеряемые частотные характеристики не зависят от того, какая точка используется для возбуждения, а какая — для изме­рения реакции.

Источник