Чем определяется период колебаний математического маятника
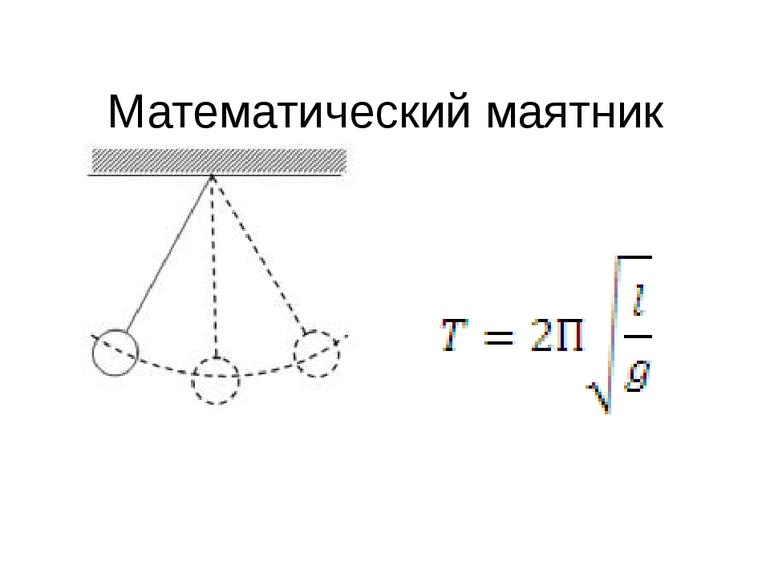
Период колебаний математического маятника
Математический маятник — что это такое
Маятник — твердое тело, которое совершает под действием приложенных сил механические колебания около неподвижной точки или оси.
Простейший маятник состоит из небольшого груза массой m, подвешенного на невесомой нити или тонком стержне длиной l и совершающего колебания под воздействием земного притяжения. Если нить считать нерастяжимой, размер груза незначительным по сравнению с длиной нити, а массу нити незначительной по сравнению с массой груза, то груз можно считать материальной точкой массой m, находящейся на постоянном расстоянии l от точки подвеса. Такой маятник называют математическим.
Определение модели системы
Математические модели динамических систем часто используют для анализа самых разных технических, социально-экономических, естественнонаучных систем, в которых происходят циклические процессы.
Существуют различные классификации динамических процессов. Одна из них изображена на схеме:
Маятник Фуко
Отсюда следует, что если бы Земля не вращалась, данного эффекта просто не существовало бы. Это обстоятельство указывает на то, что причиной неинерциальности земной системы отсчета является вращение планеты.
Центробежное ускорение на экваторе равно 0,034 м/с^2. По сравнению с экваториальным ускорением свободного падения g = 9,78 м/с^2 это величина малая, но она заметно влияет на изменение веса тела на экваторе по сравнению с его весом на полюсе. Если, например, взвешивать на пружинных весах тело массой 10 кг, то уменьшение веса на экваторе за счет действия центробежной силы составит около 35 г.
Период колебаний математического маятника
Период колебаний — время, за которое происходит одно полное колебание. В СИ измеряется в секундах.
Чему равен, от чего зависит частота
Если за время t совершается N колебаний, то период, обозначаемый буквой T, равен
где v — частота колебаний. Она обратно пропорциональна периоду.
Колебания можно изобразить в виде графика:
Источник: physik.ucoz.ru.
Период колебаний математического маятника можно рассчитать по формуле
g — ускорение свободного падения. Не зависит от амплитуды колебаний и массы груза.
В случае математического маятника она определяется длиной подвеса и ускорением свободного падения:
Для физического маятника в уравнение добавляются инерция и масса подвеса:
Для пружинного маятника частоту определяет жесткость пружины k:
Уравнения движения и их решение, формулы с примерами
Математический маятник — это материальная точка, имеющая массу m и подвешенная на нити с неизменяемой длиной l. Покидая положение равновесия, подвес совершает колебательные движения по дуге.
Это дает нам дифференциальное уравнение гармонических колебаний
Из уравнения следует, что при малых углах отклонения от положения равновесия маятник будет колебаться с периодом
Из этого следует, что
Начальная фаза зависит от того, как маятник вывели из положения равновесия. Рассмотрим ситуацию, в которой маятник отклонили от положения равновесия на расстояние А и отпустили без начальной скорости. Запишем уравнение движения колеблющегося тела с учетом того факта, что в начальный момент координата тела будет равна А:
x = A × cos ω t + φ 0 ;
Уравнение движения маятника:
Если маятник толкнули, когда он находился в положении равновесия, начальная координата колеблющейся точки будет равна нулю:
Будет ли начальная координата положительной или отрицательной, определяет выбор положительного направления оси. Если направление оси совпадет с направлением начальной скорости, то в уравнении движения будет знак «плюс», если не совпадет — знак «минус».
Уравнение движения маятника:
Рассмотрим задачи, для которых требуется составлять и решать уравнения движения.
Необходимо определить амплитуду и частоту колебаний точки, если известно, что при смещении точки от положения равновесия на 5 см ее скорость равна 6 см/с, а при смещении на 3 см — 10 см/с.
Исключаем время из системы:
x 1 2 + v 1 2 ω 2 = А 2 x 2 2 + v 2 2 ω 2 = А 2
Преобразовав выражения и подставив значения, данные в условиях задачи, получаем:
Необходимо вычислить циклическую частоту колебаний точки, если известно, что при скорости 13 см/с ускорение равнялось 6 см/с^2, а при уменьшении скорости до 12 см/с произошло увеличение ускорения до 10 см/с^2.
Решение:
Координата точки меняется по закону
Запишем уравнения скорости и ускорения точки:
Преобразуем уравнение, исключив из него А, и подставим значения, данные в условиях задачи:
Практическое применение математического маятника
С помощью математического моделирования динамических систем можно обнаружить схожесть динамических процессов в реальных физических, технических, биологических, химических и социально-экономических системах. Разработка моделей, позволяющих предсказывать время и другие характеристики периодических процессов в этих системах, является эффективным способом анализировать, например, сельскохозяйственные или производственно-экономические процессы.
Математический маятник — определение, формулы и принцип действия
Если какую-нибудь материальную точку подвесить на нить, почти не имеющей веса, то получится математический маятник Он свободно качается взад и вперёд под действием силы тяжести, которая возвращает подвешенное тело в положение равновесия, если его сместить. Математика здесь довольно сложная. Первые научные исследования в этой области принадлежат Галилео Галилею, именно они легли в основу самой точной технологии хронометража.
Простая гравитация
Так называемый простой маятник — это всего лишь идеализированная математическая модель. Это груз на конце безмассового шнура, подвешенного на оси без трения. Если его толкнуть, он будет раскачиваться с постоянной амплитудой, но с некоторыми условиями:
Дифференциальное уравнение, которое представляет движение простого маятника, выглядит следующим образом (где g — ускорение силы тяжести, ℓ — длина маятника, θ — угловое смещение): d² / dt² + g / ℓ sin θ = 0.
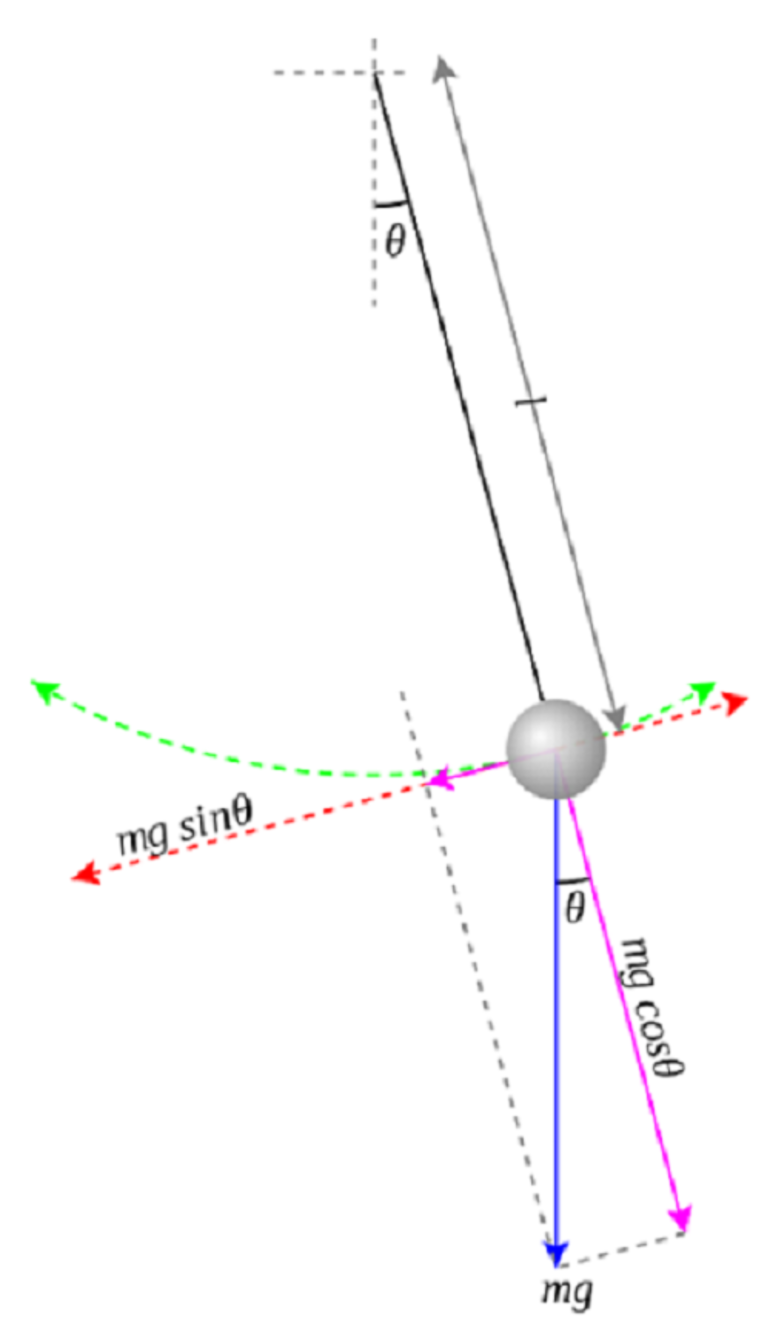
На графике 1 показаны силы, действующие на отвес. Стоит обратить внимание, что груз описывает дугу. Угол θ измеряется в радианах, и это имеет решающее значение для этой формулы. Синяя стрелка — гравитационная сила, которая действует на маятник, а фиолетовые векторы — это та же самая сила, только разложенная на компоненты, параллельные и перпендикулярные мгновенному движению груза.
Направление мгновенной скорости всегда указывается вдоль красной оси, которая считается тангенциальной, поскольку её направление всегда касается окружности. И прежде чем вывести уравнение силы деривации, стоит вспомнить второй закон Ньютона: F = ma. За F принимают сумму сил, действующих на объект, m — масса, a — ускорение.
Поскольку интерес составляет только измерение скорости, а груз вынужден оставаться на круговой траектории, уравнение Ньютона применяется только к тангенциальной оси. Короткая фиолетовая стрелка представляет компонент гравитационной силы, используя тригонометрию можно определить её величину. Таким образом, получается (g — ускорение силы тяжести вблизи поверхности земли): F = — mg sin θ = ma; a = — g sin θ.
Отрицательный знак на правой стороне означает, что θ и отвес всегда указываются в противоположных направлениях. Это вполне логично, поскольку когда маятник качается сильнее влево, ожидается, что он ускорится при движении назад — вправо. Это линейное ускорение, a вдоль красной оси может быть связано с изменением угла θ по формулам длины дуги (s): s = ℓθ; v = ds / dt = ℓdθ / dt; a = d²s / dt² = ℓd²θ / dt². Из этого следует: ℓd²θ/dt² = — gsin θ, d²θ / dt² + d / ℓ sin θ = 0.
Крутящий момент
Для начала нужно определить этот показатель на маятниковом шарнире, используя силу, вызванную гравитацией (Fg): T = ℓ x Fg, где ℓ — векторы длины маятника.
Здесь самое время рассмотреть величину крутящего момента на маятнике: |T| = — mgℓ sinθ, где m — масса, g — ускорение силы тяжести, ℓ — длина, а θ — угол между вектором длины и гравитацией. Далее, самое время переписать момент импульса: L = r x p = mr x (ꞷ x r).
Просто величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех вычислений будет выглядеть следующим образом: T = r x F = dL / dt.
Сохранение механической энергии
Такое уравнение можно получить с помощью одноимённого принципа. Формулируется он так: любой объект, падающий на вертикальное расстояние h, получит кинетическую энергию, равную той, которую потерял при падении. Изменение потенциальной энергии выражается: Δ U = mgh, тогда как кинетическая (отвес начал движение с покоя) представлена формулой: Δ K = 1/2 mu².
Поскольку, как известно, никакая энергия не теряется, выигрыш в одном должен быть равен потере в другом: 1/2 mu² = mgh.
Колебательные движения
Период колебаний математического маятника (простого гравитационного) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, от которого отвес отклоняется от вертикали θ 0, называемого амплитудой.
Он не зависит от массы груза. Если амплитуда ограничена малыми колебаниями, то на период T, время, необходимое для полного цикла является: T≈ 2 π √ L/g. При этом L — длина маятника, а g — местное ускорение гравитации.
Нужно сказать, что для небольших колебаний период не зависит от амплитуды. Такое свойство называется изохронизмом, именно оно стало причиной того, что маятники используются для хронометража. Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое количество времени. Для большого размаха свойственно увеличение периода с каждым раскачиванием, поэтому он длиннее, чем задано уравнением, отражающим частоту колебаний математического маятника.
Период возрастает до бесконечности как только θ 0 приближается к 180°, так как это значение является нестабильной точкой равновесия для маятника. Истинный период может быть записан в нескольких различных формах, например, бесконечный ряд: T = 2 π √ L/g )1+ 1/16 θ²/º + 11/3072 θ ⁴/º + …). Разница между истинным и периодом небольших колебаний называется круговой ошибкой. В случае с типичными напольными часами, у которых маятник имеет размах 6° и, следовательно, амплитуду 3° (0,05 радиана), разница составит около 15 секунд в день.
Формула математического маятника, при малых колебаниях, когда он приближается к гармоническому осциллятору, и его движение, как функция времени t, находит выражение следующим образом: θ(t) = θₒ cos (2 π / T * t + ⱷ). Где фи (ⱷ) — постоянная величина, зависящая от начальных условий. Для маятников этот период незначительно меняется в зависимости от некоторых факторов, например:
Если необходимы точные расчёты, конечно, все эти поправки должны учитываться.
Составной маятник
Другое название — физический, представляет собой любое качающееся твёрдое тело, свободно вращающееся вокруг фиксированной горизонтальной оси. Соответствующая эквивалентная длина — L, а для расчёта времени используется расстояние от оси до центра колебаний. Эта точка расположена над центром массы на расстоянии от оси, традиционно называемым радиусом колебаний, который зависит от распределения веса груза.
Христиан Гюйгенс в 1673 году доказал, что точка вращения и центр колебаний взаимозаменяемы. Это означает, если какой-либо маятник перевёрнут и ротирован от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр будет находиться в старой точке вращения.
В 1817 году Генри Кэтер использовал эту идею для создания обратимого маятника, теперь известного под именем создателя, для улучшения измерений ускорения под действием силы тяжести.
Историческая хроника
Одним из самых ранних известных применений маятника было устройство сейсмометра (I века) китайского учёного династии Хань Чжан Хэна. Его функция состояла в том, чтобы раскачивать и активировать один из серии рычагов после того, как он был нарушен тремором землетрясения, которое происходило далеко от места измерения. Освобождённый рычагом, маленький шарик выпадал из устройства в форме урны в одну из восьми горловин металлической жабы внизу, в восьми точках компаса, что указывало направление землетрясения.
Многие источники утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году с британским историком Эдвардом Бернардом.
В эпоху Возрождения большие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы. Леонардо Давинчи сделал много рисунков движения маятников, хотя и не осознавал его значения для хронометража.
Исследования Галилея
Итальянский учёный Галилео Галилей был первым, кто начал изучать свойства маятников, начиная примерно с 1602 года. Самый ранний существующий отчёт о его исследованиях содержится в письме Гвидо Убальдо дель Монте из Падуи от 29 ноября 1602 года. Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес был вызван около 1582 года, когда физик раскачивал люстры в соборе Пизы.
Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометриста, называемое изохронизмом; период маятника приблизительно не зависит от амплитуды или ширины качания. Он также обнаружил, что период не зависит от массы отвеса и пропорционален квадратному корню из длины всей конструкции. Сначала он использовал маятники свободного вращения в простых приложениях синхронизации.
Его друг — врач Санторио Санторий, используя наработки Галилея, изобрёл прибор, который измерял пульс пациента. В 1641 году Галилео задумал и продиктовал своему сыну Винченцо конструкцию маятниковых часов. Тот начал строительство, но не завершил его, поскольку умер в 1649 году. Так, появился первый гармонический осциллятор, использованный человеком.
Маятниковые часы
Первый образец построил в 1656 году голландский учёный Христиан Гюйгенс. Это было значительное улучшение по сравнению с существующими механическими часами. Их точность была улучшена с отклонений от 15 минут до 15 секунд в день. Маятники распространились по Европе, так как все существующие часы стали модифицироваться.
Английский учёный Роберт Гук изучил конический маятник (около 1666), который мог свободно колебаться в двух измерениях, а груз вращаться по кругу или эллипсу. Он использовал движение этого устройства в качестве модели для анализа орбитального движения планет. Гук предложил Исааку Ньютону в 1679 году свои наработки.
Он утверждал, что составляющие орбитального движения состояли из инерционного движения по касательному направлению и привлекательного движения в радиальном направлении. Это сыграло свою роль в формулировке Ньютоном закона всемирного тяготения. Роберт Гук также был ответственным за то, что ещё в 1666 году предположил, что маятник можно использовать для измерения силы тяжести.
Во время своей экспедиции в Кайенна (Французская Гвиана) в 1671, Жан Рише обнаружил, что там часы с маятником шли на 2,5 минуты медленнее, чем в Париже. Из этого он сделал вывод, что сила гравитации была ниже в Кайенне. В 1687 году Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля была не настоящей сферой, а слегка сплюснутой (сплющенной на полюсах) от действия центробежной силы из-за её вращения, это и вызывает увеличение силы гравитации.
Портативные маятники стали совершать рейсы в дальние страны, в качестве прецизионных гравиметров для измерения ускорения свободного падения в разных точках Земли, что в итоге привело к определению точной модели формы планеты. Затем последовало превращение исследований и выводов учёных в новые классы приборов, с дополнительными параметрами. Например:
В 1930 году решение задачи по точному хронометражу было найдено, в 1921 был изобретён кварцевый генератор.
Математический маятник
Содержание:
Определение
Представьте себе некую механическую систему, которая состоит из некой материальной точки (тела), которая висит на нерастяжимой невесомой нити (при этом масса нити ничтожно мала по сравнению с массой тела). Вот такая механическая система и является маятником или осциллятором, как его еще называют. Впрочем, могут быть и другие виды такого устройства. Чем же математический маятник, осциллятор интересен для нас? Дело в том, что с его помощью можно проникнуть в суть многих интересных природных явлений в физике.
Колебания
Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.
Маятниковые часы Гюйгенса.
Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.
Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:
Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.
Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.
Свойства
У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.
В ходе наблюдений за маятниками были выведены следующие закономерности:
Период
Период маятника – показатель, который представляет период собственно колебаний маятника, их длительность. Формулу периода математического маятника можно записать следующим образом.
Где L – длина нити математического маятника, g – ускорение свободного падения, а π – число Пи, математическая константа.
Период малых колебания математического маятника никак не зависит от массы маятника и амплитуды колебания, в этой ситуации он двигается как математический маятник с заданной длинной.
Практическое применение
Вот мы добрались и до самого интересного, зачем нужен математический маятник и какое его применение на практике в жизни. В первую очередь ускорение математического маятника используется для геологоразведки, с его помощью ищут полезные ископаемые. Как это происходит? Дело в том, что ускорение свободного падения изменяется с географической широтой, так как плотность коры в разных местах нашей планеты далеко не одинакова и там где залегают породы с большей плотностью, ускорение будет немножко больше. А значит, просто подсчитав количество колебаний маятника можно отыскать в недрах Земли руду или каменный уголь, так как они имеют большую плотность, нежели другие рыхлые горные породы.
Также математическим маятником пользовались многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего.
Видео
И в завершение образовательное видео по теме нашей статьи.
Простая гравитация
Так называемый простой маятник — это всего лишь идеализированная математическая модель. Это груз на конце безмассового шнура, подвешенного на оси без трения. Если его толкнуть, он будет раскачиваться с постоянной амплитудой, но с некоторыми условиями:
На графике 1 показаны силы, действующие на отвес. Стоит обратить внимание, что груз описывает дугу. Угол θ измеряется в радианах, и это имеет решающее значение для этой формулы. Синяя стрелка — гравитационная сила, которая действует на маятник, а фиолетовые векторы — это та же самая сила, только разложенная на компоненты, параллельные и перпендикулярные мгновенному движению груза.
Крутящий момент
Просто величина углового момента и его производная по времени: |L| = mr² w = mℓ² d²θ / dt². Формула крутящего момента после всех вычислений будет выглядеть следующим образом: T = r x F = dL / dt.
Сохранение механической энергии
Такое уравнение можно получить с помощью одноимённого принципа. Формулируется он так: любой объект, падающий на вертикальное расстояние h, получит кинетическую энергию, равную той, которую потерял при падении. Изменение потенциальной энергии выражается: Δ U = mgh, тогда как кинетическая (отвес начал движение с покоя) представлена формулой: Δ K = 1/2 mu².
Поскольку, как известно, никакая энергия не теряется, выигрыш в одном должен быть равен потере в другом: 1/2 mu² = mgh.
Колебательные движения
Период колебаний математического маятника (простого гравитационного) зависит от его длины, локальной силы тяжести и в небольшой степени от максимального угла, от которого отвес отклоняется от вертикали θ 0, называемого амплитудой.
Нужно сказать, что для небольших колебаний период не зависит от амплитуды. Такое свойство называется изохронизмом, именно оно стало причиной того, что маятники используются для хронометража. Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое количество времени. Для большого размаха свойственно увеличение периода с каждым раскачиванием, поэтому он длиннее, чем задано уравнением, отражающим частоту колебаний математического маятника.
Формула математического маятника, при малых колебаниях, когда он приближается к гармоническому осциллятору, и его движение, как функция времени t, находит выражение следующим образом: θ(t) = θₒ cos (2 π / T * t + ⱷ). Где фи (ⱷ) — постоянная величина, зависящая от начальных условий. Для маятников этот период незначительно меняется в зависимости от некоторых факторов, например:
Если необходимы точные расчёты, конечно, все эти поправки должны учитываться.
Составной маятник
Христиан Гюйгенс в 1673 году доказал, что точка вращения и центр колебаний взаимозаменяемы. Это означает, если какой-либо маятник перевёрнут и ротирован от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, и новый центр будет находиться в старой точке вращения.
В 1817 году Генри Кэтер использовал эту идею для создания обратимого маятника, теперь известного под именем создателя, для улучшения измерений ускорения под действием силы тяжести.
Историческая хроника
Одним из самых ранних известных применений маятника было устройство сейсмометра (I века) китайского учёного династии Хань Чжан Хэна. Его функция состояла в том, чтобы раскачивать и активировать один из серии рычагов после того, как он был нарушен тремором землетрясения, которое происходило далеко от места измерения. Освобождённый рычагом, маленький шарик выпадал из устройства в форме урны в одну из восьми горловин металлической жабы внизу, в восьми точках компаса, что указывало направление землетрясения.
Многие источники утверждают, что египетский астроном X века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году с британским историком Эдвардом Бернардом.
В эпоху Возрождения большие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы. Леонардо Давинчи сделал много рисунков движения маятников, хотя и не осознавал его значения для хронометража.
Исследования Галилея
Итальянский учёный Галилео Галилей был первым, кто начал изучать свойства маятников, начиная примерно с 1602 года. Самый ранний существующий отчёт о его исследованиях содержится в письме Гвидо Убальдо дель Монте из Падуи от 29 ноября 1602 года. Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес был вызван около 1582 года, когда физик раскачивал люстры в соборе Пизы.
Галилей обнаружил важнейшее свойство, которое делает маятники полезными в качестве хронометриста, называемое изохронизмом; период маятника приблизительно не зависит от амплитуды или ширины качания. Он также обнаружил, что период не зависит от массы отвеса и пропорционален квадратному корню из длины всей конструкции. Сначала он использовал маятники свободного вращения в простых приложениях синхронизации.
Его друг — врач Санторио Санторий, используя наработки Галилея, изобрёл прибор, который измерял пульс пациента. В 1641 году Галилео задумал и продиктовал своему сыну Винченцо конструкцию маятниковых часов. Тот начал строительство, но не завершил его, поскольку умер в 1649 году. Так, появился первый гармонический осциллятор, использованный человеком.
Маятниковые часы
Первый образец построил в 1656 году голландский учёный Христиан Гюйгенс. Это было значительное улучшение по сравнению с существующими механическими часами. Их точность была улучшена с отклонений от 15 минут до 15 секунд в день. Маятники распространились по Европе, так как все существующие часы стали модифицироваться.
Английский учёный Роберт Гук изучил конический маятник (около 1666), который мог свободно колебаться в двух измерениях, а груз вращаться по кругу или эллипсу. Он использовал движение этого устройства в качестве модели для анализа орбитального движения планет. Гук предложил Исааку Ньютону в 1679 году свои наработки.
Он утверждал, что составляющие орбитального движения состояли из инерционного движения по касательному направлению и привлекательного движения в радиальном направлении. Это сыграло свою роль в формулировке Ньютоном закона всемирного тяготения. Роберт Гук также был ответственным за то, что ещё в 1666 году предположил, что маятник можно использовать для измерения силы тяжести.
Во время своей экспедиции в Кайенна (Французская Гвиана) в 1671, Жан Рише обнаружил, что там часы с маятником шли на 2,5 минуты медленнее, чем в Париже. Из этого он сделал вывод, что сила гравитации была ниже в Кайенне. В 1687 году Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля была не настоящей сферой, а слегка сплюснутой (сплющенной на полюсах) от действия центробежной силы из-за её вращения, это и вызывает увеличение силы гравитации.
Портативные маятники стали совершать рейсы в дальние страны, в качестве прецизионных гравиметров для измерения ускорения свободного падения в разных точках Земли, что в итоге привело к определению точной модели формы планеты. Затем последовало превращение исследований и выводов учёных в новые классы приборов, с дополнительными параметрами. Например:
В 1930 году решение задачи по точному хронометражу было найдено, в 1921 был изобретён кварцевый генератор.