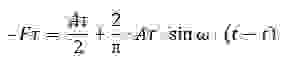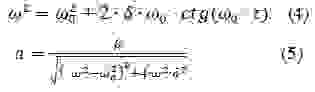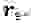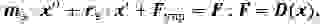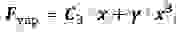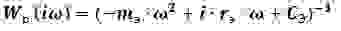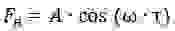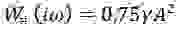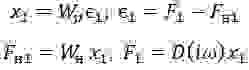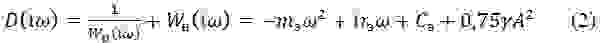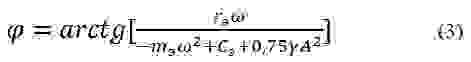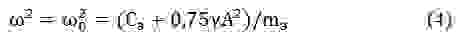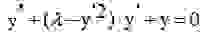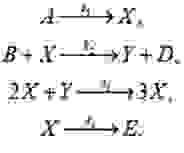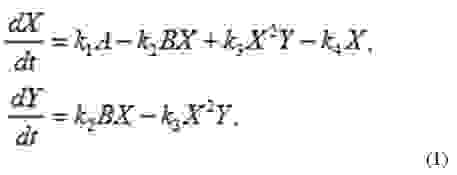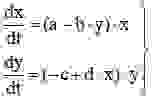Чем определяется период автоколебаний
Автоколебания
Всего получено оценок: 163.
Всего получено оценок: 163.
Из курса физики за 11 класс известно, что колебания — это изменение некоторого параметра системы вокруг среднего значения. Одним из видов колебаний являются автоколебания. Рассмотрим суть и особенности автоколебаний, дадим их определение.
Автоколебательные системы
В любой реальной системе происходят потери энергии. Любые колебания в реальных условиях не могут обходиться без притока энергии. Поэтому незатухающие колебания в реальности всегда являются вынужденными. Они постоянно получают энергию, которая компенсирует потери.
Рис. 1. Свободные и вынужденные колебания.
Однако процесс пополнения энергии может происходить по-разному. Например, поршень насоса колеблется под действием сил, приложенных к нему через механизм от ведущего вала. Здесь колебания поршня происходят с частотой, задаваемой извне, и вся подводимая энергия сразу же уходит на продвижение перекачиваемой жидкости.
Возможен другой вариант пополнения энергии — маятник часов. С каждым качанием маятник пополняет запасы энергии от анкерного механизма. Существенное отличие здесь состоит в том, что частота пополнения энергии в маятнике регулируется самим маятником.
Если в случае насоса параметры неважны — колебания будут всё равно происходить с частотой, задаваемой валом, — то в случае маятника ситуация другая. Увеличив жесткость пружины или массу баланса, мы изменим частоту колебаний, поскольку качающийся маятник изменит частоту подведения энергии от анкерного механизма.
Системы, в которых незатухающие колебания существуют за счет поступления энергии в систему под ее же управлением, называются автоколебательными. Колебания, возникающие в таких системах, называются автоколебаниями. В отличие от вынужденных колебаний, автоколебания существуют в системе без поступления внешних воздействий.
Таким элементом, как правило, является транзистор. Часть напряжения на катушке поступает на управляющий электрод транзистора (базу), и через участок коллектор-эмиттер транзистора энергия добавляется в контур.
Рис. 2. Схема генератора на транзисторе.
Элементы автоколебательной системы
Выделим элементы автоколебательной системы:
В любой автоколебательной системе есть эти элементы. Отсутствие любого из них приводит к тому, что колебания становятся затухающими или вовсе невозможны.
Что мы узнали?
Автоколебательная система — это система, колебания в которой совершаются под управлением самой системы. Простейшими примерами из жизни автоколебательных систем является маятник часов или генератор на транзисторе. Колебания, возникающие в автоколебательных системах, называются автоколебаниями.
Автоколебания
Автоколеба́ния — незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия. [1]
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Термин автоколебания в русскоязычную терминологию введён А. А. Андроновым в 1928 году.
Содержание
Примеры
Примерами автоколебаний могут служить:
Молоток Маклакова
Катушка L колебательного контура помещается над столом (или другим предметом, по которому требуется ударять). Снизу в неё входит железная трубка, нижний конец которой является ударной частью молотка. В трубке есть вертикальная прорезь, чтобы уменьшить токи Фуко. Параметры колебательного контура такие, что собственная частота его колебаний совпадает с частотой тока в цепи (например, переменного городского тока, 50 герц).
Трубка совершает автоколебания, т. е. периодические движения вверх и вниз, и при этом громко стучит по столу, подобно молотку. Период этих механических автоколебаний в десятки раз превосходит период переменного тока, поддерживающего их.
Молоток назван по имени М. И. Маклакова, лекционного ассистента Московского физико-технического института, предложившего и осуществившего такой опыт для демонстрации автоколебаний.
Механизм автоколебаний
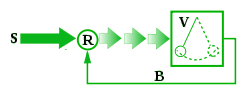
Автоколебания могут иметь различную природу: механическую, тепловую, электромагнитную, химическую. Механизм возникновения и поддержания автоколебаний в разных системах может основываться на разных законах физики или химии. Для точного количественного описания автоколебаний разных систем может потребоваться разный математический аппарат. Тем не менее, можно представить схему, общую для всех автоколебательных систем, качественно описывающую этот механизм (рис. 1).
На схеме: S — источник постоянного (непериодического) воздействия; R — нелинейный регулятор, преобразующий постоянное воздействие в переменное (например, в прерывистое во времени), которое и «раскачивает» колеблющийся элемент (элементы) системы V, а колебания через обратную связь B управляют работой регулятора R, задавая фазу и частоту его действия. Диссипация (рассеивание энергии) в автоколебательной системе восстанавливается за счёт поступления в неё энергии из источника постоянного воздействия, благодаря чему автоколебания не затухают.
Если колеблющийся элемент системы способен к собственным затухающим колебаниям (т.н. гармонический диссипативный осциллятор), автоколебания (при равенстве диссипации и поступления энергии в систему за время периода) устанавливаются на частоте, близкой к резонансной для этого осциллятора, их форма становится близкой к гармонической, а амплитуда, в некотором диапазоне значений, тем больше, чем больше величина постоянного внешнего воздействия.
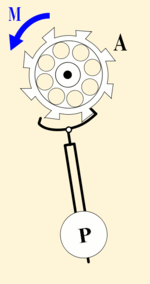
Примером такого рода системы может служить храповой механизм маятниковых часов, схема которого представлена на рис. 2. На ось храпового колеса A (которое в этой системе выполняет функцию нелинейного регулятора) действует постоянный момент силы M, передающийся через зубчатую передачу от заводной пружины или от гири. При вращении колеса A его зубцы сообщают кратковременные импульсы силы маятнику P (осциллятору), благодаря которым его колебания не затухают. Кинематика механизма играет роль обратной связи в системе, синхронизируя вращение колеса с колебаниями маятника таким образом, что за полный период колебания колесо поворачивается на угол, соответствующий одному зубцу.
Автоколебательные системы, не содержащие осцилляторов, называются релаксационными. Колебания в них могут сильно отличаться от гармонических, и иметь прямоугольную, треугольную или трапециедальную форму. Амплитуда и период релаксационных автоколебаний определяются соотношением величины постоянного воздействия и характеристик инерционности и диссипации системы.
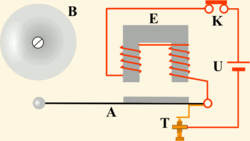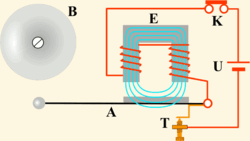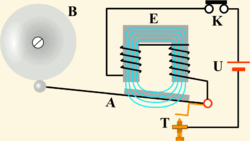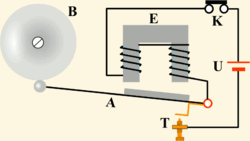
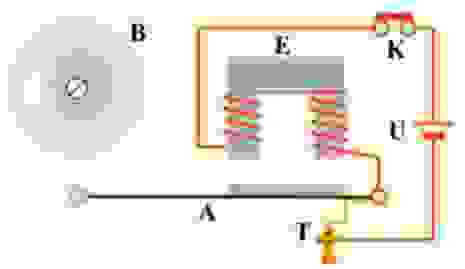
Простейшим примером релаксационных автоколебаний может служить работа электрического звонка, изображённого на рис. 3.. Источником постоянного (непериодического) воздействия здесь является электрическая батарея U; роль нелинейного регулятора выполняет прерыватель T, замыкающий и размыкающий электрическую цепь, в результате чего в ней возникает прерывистый ток; колеблющимися элементами являются магнитное поле, периодически наводимое в сердечнике электромагнита E, и якорь A, движущийся под воздействием переменного магнитного поля. Колебания якоря приводят в действие прерыватель, что и образует обратную связь.
Инерционность этой системы определяется двумя различными физически величинами: моментом инерции якоря А и индуктивностью обмотки электромагнита E. Увеличение любого из этих параметров приводит к увеличению периода автоколебаний.
При наличии в системе нескольких элементов, колеблющихся независимо друг от друга, и одновременно воздействующих на нелинейный регулятор или регуляторы (которых тоже может быть несколько), автоколебания могут принимать более сложный характер, например, апериодический, или динамический хаос.
В природе и технике
Автоколебания лежат в основе многих явлений природы:
На автоколебаниях основан принцип действия большого количества всевозможных технических устройств и приспособлений, в том числе:
В то же время, в некоторых технических системах автоколебания могут возникать без специального намерения конструкторов этих систем, в результате неудачного выбора их технических параметров. Такие автоколебания могут быть нежелательными (например, «рычание» водопроводного крана при определённых расходах воды), а зачастую разрушительными, являющимися причиной аварий c тяжёлыми последствиями, когда речь идёт о системах с большими уровнями энергии, циркулирующей в них. Например:
Автоколебания и резонанс
Здравствуйте!
В связи с вопросами читателей моей публикации [1] касательно условий возбуждения автоколебаний в механической системе, я решил описать явление возникновения и поддержания автоколебаний подробно, выделив основные области возникновения и применения автоколебаний.
В википедии автоколебания объясняют так [2]:
Незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. При этом частота становится почти равной резонансной.
Автоколебания в технике
Автоколебательная система с запаздыванием (на примере электромеханического звонка)
Приведём пример электромеханического звонка:
При замыкании цепи кнопкой (К) электромагнит (Е) притягивает ударник, ударник бьёт по звонку и размыкает цепь питания электромагнита, механически связанным с ним контактом (Т) ударник (А) возвращается назад и процесс повторяется.
При рассмотрении процесса возникновения автоколебаний будем считать, что сила, действующая на боёк (А) звонка, изменяется пропорционально изменению тока в RL цепи.
Такое допущение сделано для упрощения рассмотрения, поскольку зависимость силы от тока в обмотке и зазора между бойком и полюсами значительно сложнее [3].
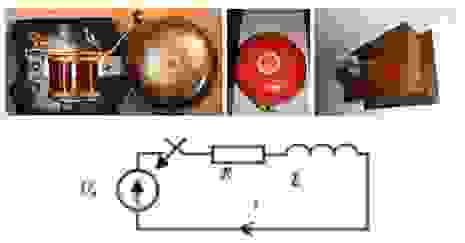
Ниже приведены конструкции электромеханических звонков и их упрощённая электрическая схема:
Боёк колеблется относительно установленного зазора согласно соотношению A*sin (w*t).
Решив численным методом дифференциальное уравнение RL цепи с начальными условиями
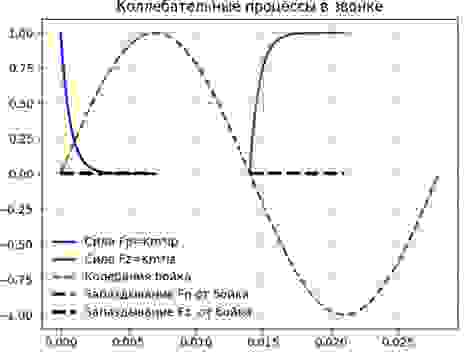
для замыкания и размыкания контакта, наложив на эти решения колебания бойка, получим:
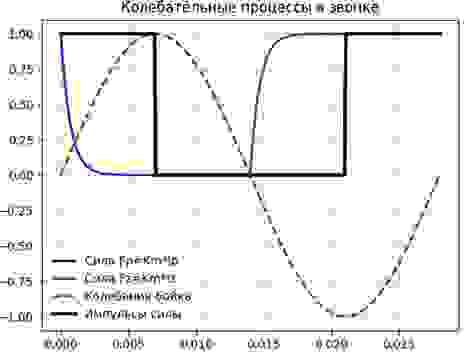
Для приближенной теории будем считать, что сила Fτ, выраженная последовательностью прямоугольных импульсов, которые возникает и исчезает мгновенно, но не в момент срабатывания контакта, а с запаздыванием τ=L/R. Добавим Fτ на график, получим:
Обозначим амплитуду силы Fτ через Aτ, получим разложения этой силы в ряд Фурье [4] (учитывая что x=a∙sin(ω∙t), для первых двух членов ряда:
Будем считать, что постоянная составляющая силы Aτ/2 компенсируется регулировкой.
Тогда уравнение для колебаний бойка с учётом его приведенной массы m, трения r и изгибной жёсткости k примет вид:
(1)
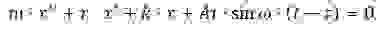
Разделим обе части на массу бойка, введем обозначения,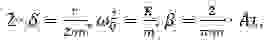 
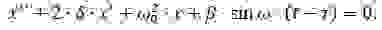
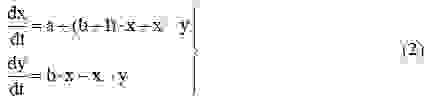
получим:
(2)
Для того, чтобы получить аналитические соотношения для частоты и амплитуды колебаний бойка, решим (2) приближённым методом [5]. Преобразуем (2) к виду:
(3)
Подставив в (3)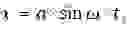 
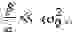
при условии: 
пропуская промежуточные выкладки получим соотношения для частоты и амплитуды автоколебаний:
На основании приведенных соотношений можно сделать вывод, что, при отсутствии самоиндукции, звонок работать не может, поскольку при L=0 нет запаздывания τ=0. Таким образом, при нулевом запаздывании автоколебания не возможны.
Автоколебания в измерительной технике (на примере механического резонатора вибрационных плотномеров)
Механические резонаторы в виде трубок пластин или цилиндров широко используются в вибрационных плотномерах, внешний вид которых приведен на рисунках:
Будем рассматривать резонатор c сосредоточенными эквивалентными параметрами: массой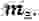 
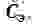
жесткостью 
и трением, характеризуемым коэффициентом 
Такая замена вполне допустима в ограниченной области частот при соблюдении равенства собственных частот колебаний обеих систем, а также равенства потерь энергии и обусловленных ими затуханий.
Запишем систему уравнений, описывающих движение резонатора в замкнутой системе возбуждения:
где: F- сила воздействия системы возбуждения на резонатор;
D(x)- неизвестный оператор обратной связи, подлежащий определению; Fупр — упругая восстанавливающая сила резонатора, которая в общем случае может описываться нелинейной функцией; х — поперечное смещение эквивалентной массы.
Воспользуемся выражением кубической упругой характеристики резонатора:
где γ — коэффициент, характеризующий отклонение реальной упругой характеристики от линейной.
Преобразуем записанную систему равенства к виду:
где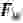 
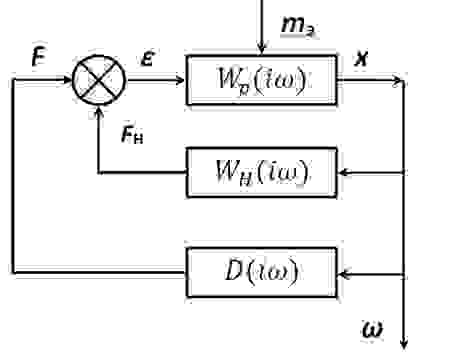
— нелинейная составляющая упругой силы.
Структурная схема автоколебательной системы, работа которой характеризуется уравнениями, (1) приведена на рисунке:
Схема содержит нелинейное звено, выполняющее функцию корректирующей обратной связи линейного резонатора, имеющего частотную характеристику:
Для решения задачи синтеза оптимальной системы возбуждения, воспользуемся методом гармонической линеаризации [6].
Механические резонаторы являются высокодобротными колебательными системами, которые можно рассматривать как узкополосные фильтры с выходным сигналом вида: x
A∙cos(ω∙τ), где A— амплитуда колебаний резонатора; ω — частота колебаний, близкая к резонансной [7].
Поэтому для нелинейного элемента справедливо соотношение:
Пренебрегая третьей гармоникой, отфильтрованной линейной частью резонатора, частотную характеристику линеаризованного звена нелинейной упругости механического резонатора можно в виде:
Рассмотрим уравнение для первой гармоники колебаний линеаризованной системы:
Для определения вида частотной характеристики D(iω), обеспечивающей совместность этой системы, исключим промежуточные переменные прямой подстановкой их выражений через другие переменные. В результате получим:
Из соотношения (2) определим смещение фазы, осуществляемое системой возбуждения:
Нетрудно установить, что частота автоколебаний не будет зависеть от трения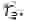 
при сдвиге фазы φ=π/2, тогда:
При этом условии из (2) следует, что система возбуждения должна быть дифференцирующим звеном D(iω)=(i*rэ* ω) т.е.
Из (5) следует, что частотная характеристика цепи обратной связи системы возбуждения должна быть пропорциональна коэффициенту трения
Система возбуждения состоит из трех элементов, D(iω)=Dп* Dу* D(в ), характеризующих частотные характеристики: приемника Dп, усилителя Dу и возбудителя D(в ) колебаний. Приемник является дифференцирующим – Dп=Kп* i*ω, а возбудитель усилительным
звеном – Dв=Kв.
Для выполнения условия (5) усилитель должен иметь частотную характеристику:
Коэффициент усиления должен меняться вместе с изменением трения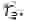
Звено с переменным коэффициентом усиления можно реализовать простейшей нелинейностью типа двухпозиционного реле, имеющей частотную характеристику по первой гармонике [6]:
где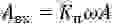 
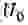
— амплитуда первой гармоники на входе усилителя; 
— выходное напряжение усилителя, подаваемое на возбудитель колебаний.
Из (6) и (7) можно получить выражение для амплитуды установившихся автоколебаний резонатора:
Для устранения этого влияния амплитуды на частоту резонатора можно стабилизировать амплитуду A варьированием напряжения U0 с помощью регулятора, стабилизирующего амплитуду входного сигнала Aвх, поступающего с приемника колебаний.
Из изложенного можно сделать вывод, что частота автоколебаний резонатора вибрационного измерительного преобразователя не будет зависеть от трения при сдвиге фазы φ=π/2, когда система возбуждения является дифференцирующим звеном, и не будет зависит от амплитуды автоколебаний при стабилизации входного сигнала этого звена.
Автоколебания в радиотехнических генераторах (на примере решения уравнения
Ван-дер-Поля)
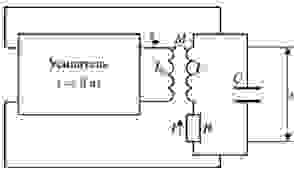
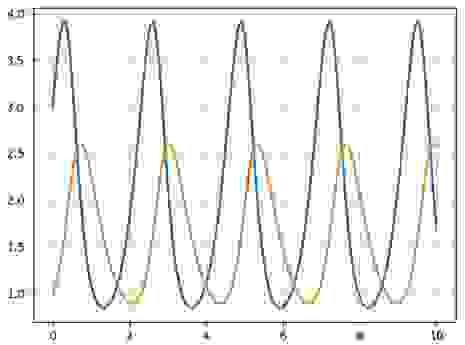
Обобщённая схема радиотехнического генератора автоколебаний приведена на рисунке:
Механизм возбуждения автоколебаний в генераторе можно качественно описать следующим образом. Даже при отсутствии напряжения на выходе усилителя напряжение в контуре испытывает случайные флуктуации. Они усиливаются усилителем и вновь поступают в контур через цепь обратной связи.
При этом из шумового спектра флуктуаций будет выделяться составляющая на собственной частоте высокодобротного контура. Если энергия, вносимая в контур таким образом, превосходит энергию потерь, амплитуда колебаний нарастает.
Основной моделью, описывающей автоколебания в радиотехническом генераторе, является уравнение Ван-дер-Поля. Приведём уравнение Ван-дер-Поля к виду, содержащему единственный управляющий параметр с безразмерными переменными:
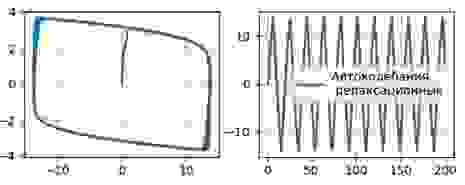
Получим фазовые портреты (слева) и временные реализации колебаний (справа) осциллятора Ван-дер-Поля: λ =0.1, λ =1.1
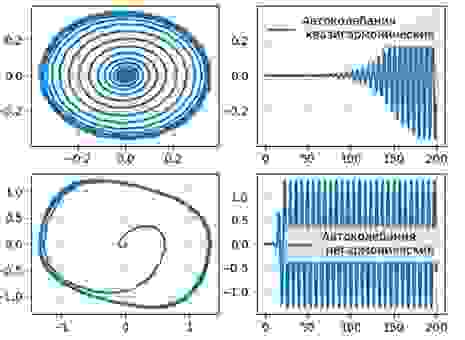
Для λ =10.0
Уравнение Ван-дер-Поля имеет единственную особую точку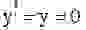 
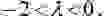
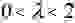
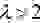
, которая является устойчивым узлом при 
устойчивым фокусом при 
неустойчивым фокусом при 
и неустойчивым узлом при 
. Если выполнено условие самовозбуждения, на фазовой плоскости имеется также предельный цикл, отвечающий режиму периодических автоколебаний.
Химические колебания. Брюсселятор
Важным и нетривиальным примером автоколебательных процессов служат некоторые химические реакции. Химические колебания — это колебания концентраций реагирующих веществ.
К настоящему времени известно достаточно много колебательных реакций. Наиболее знаменитая из них была открыта Б.П. Белоусовым в 1950 г. и позднее детально изучена А.М. Жаботинским. Реакция Белоусова — Жаботинского (БЖ) представляет собой процесс окисления малоновой кислоты при взаимодействии в присутствии ионов в качестве катализатора.
В ходе реакции раствор периодически изменяет свой цвет: голубой — красный — голубой — красный и т.д. Кроме простых периодических колебаний, реакция БЖ демонстрирует (в зависимости от условий эксперимента) множество различных типов пространственно-временной динамики, которые окончательно еще не исследованы.
Предложены различные математические модели реакции БЖ (например, модель Филда, Кереса и Нойеса — «орегонатор»), однако ни одна из них не описывает полностью все детали, наблюдаемые в эксперименте.
Мы рассмотрим более простой модельный пример: гипотетическую химическую реакцию, которая получила название Брюсселятор [8]. Уравнения этой реакции имеют вид:
Предполагается, что реагенты A и B имеются в избытке, так что их концентрации можно считать постоянными, а D и E ни в какие реакции не вступают. Составим кинетические уравнения, соответствующие реакции, которые описывают динамику концентраций реагирующих веществ.
Поскольку число актов химической реакции в единицу времени определяется вероятностью столкновения молекул реагентов, скорости изменения концентраций продуктов реакции пропорциональны произведению концентраций соответствующих реагентов с коэффициентами пропорциональности, называемыми константами скоростей реакций. Тогда кинетические уравнения можно записать в виде:
Символами Y,X будем теперь обозначать соответствующие концентрации. Отметим, что из третьего уравнения системы следует, что скорость образования вещества X зависит от его концентрации, т.е. эта стадия реакции носит автокаталитический характер. Приведем уравнения (1) к безразмерному виду, содержащему минимальное число управляющих параметров. Для этого перейдём к новым переменным,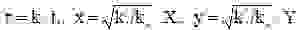 
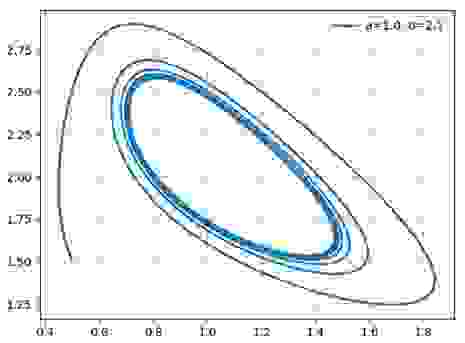
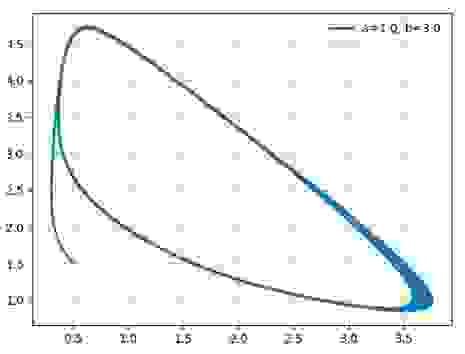
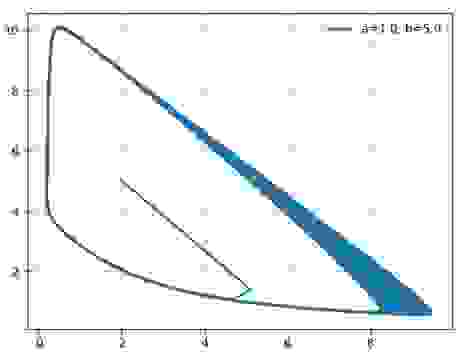
Тогда уравнения (1) примут вид:
Построим фазовые портреты для: a=1.0; b=2.1; b=3.0;b=5.0
Таким образом, химический осциллятор демонстрирует поведение, типичное для автоколебательных систем и вполне аналогичное, например, осциллятору Ван-дер-Поля.
В динамике популяций есть много примеров, когда изменение численности популяций во времени носит колебательный характер. Одним из самых известных примеров описания динамики взаимодействующих популяций являются уравнения Вольтерра—Лотка.
Развитие популяции хищников зависит от количества пищи (жертв), при отсутствии пищи ( x=0 ) относительная скорость изменения популяции хищников равна y’/y =-c, c>0, наличие пищи компенсирует убывание, и при x>0 имеем y’/y =(-c +d*x), d>0.
Таким образом, система Вольтерра—Лотка имеет вид:
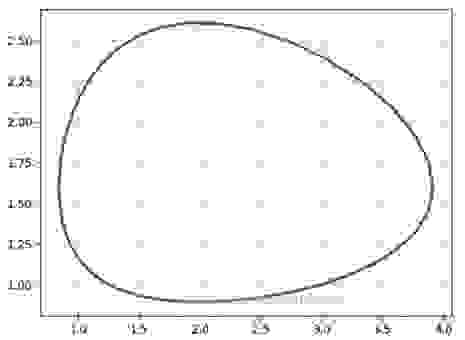
Рассмотрим фазовый портрет системы Вольтерра Лотка, для a=4 b=2.5, c=2, d=1 и графики ее решения с начальным условием x(0)=3, y(0)=1, построенные программой Python для численного решения системы обыкновенных дифференциальных уравнений:
Видно, что процесс имеет колебательный характер. При заданном начальном соотношении числа особей обоих видов 3: 1, обе популяции сначала растут. Когда число хищников достигает величины b=2.5, популяция жертв не успевает восстанавливаться и число жертв начинает убывать.
Уменьшение количества пищи через некоторое время начинает сказываться на популяции хищников и когда число жертв достигает величины x=c/d =2 (в этой точке y’=0), число хищников тоже начинает сокращаться вместе с сокращением числа жертв. Сокращение популяций происходит до тех пор, пока число хищников не достигнет величины y=a/b =1.6 (в этой точке x’=0).
С этого момента начинает расти популяция жертв, через некоторое время пищи становится достаточно, чтобы обеспечить прирост хищников, обе популяции растут, и… процесс повторяется снова и снова.
Рассмотренная модель может описывать поведение конкурирующих фирм, рост народонаселения, численность воюющих армий, изменение экологической обстановки, развитие науки и т.п.