Чем определяется адекватность математических моделей
ЦП Автоматизированные системы управления и промышленная безопасность
БК Автоматизированные системы управления и кибернетика
10. Адекватность и эффективность математических моделей.
10. Адекватность и эффективность математических моделей.
Вопрос о необходимой и достаточной степени соответствия объекту – оригиналу или адекватности модели относится к числу важнейших в сфере модельной методологии. Под эффективностью понимают практическую полезность. Процесс моделирования неизбежно протекает в условиях диалектического взаимодействия двух противостоящих друг другу тенденций. С одной стороны, исследователь всегда стремиться к возможно более полному и точному воспроизведению в модели свойств и характеристик объекта. Неизбежным следствием такого подхода является рост сложности, которая проявляется в числе переменных, числе учитываемых связей и влияний, повышении требования к точности исходных данных и т.д. Именно эта сторона дела – требование полноты соответствия модели объекту – оригиналу акцентируется в большинстве философских работ и даже рассматривается некоторыми авторами как мера совершенства модели. Однако практика показала неопровержимо: эффективность модели находится в обратной зависимости от её сложности, быстро убывая с ростом последней.
Определить математическим путем наилучшее сочетание полноты-точности создаваемой модели с одной стороны и простоты с другой, практически никогда не удается из-за неформализуемости и неоднозначности большей части подлежащих учету факторов.
Пара задача-объект в основном определяет номенклатуру подлежащих учету переменных объекта; параметры, входящие в модель, число и характер связей между ними, требования к точности данных и ряд других важнейших характеристик модели. Решающим фактором эффективности сейчас оказывается математический аппарат. Эффективность модели зависит и от такого субъективного момента, как профессиональные качества и уровень подготовки исследователя – исполнителя.
Таким образом, можно сделать заключение: наилучшее в практическом отношении качество или эффективность любой модели достигается как разумный компромисс между близостью модели к оригиналу (адекватностью) и простотой, обеспечивающей возможность и удобство использования модели по её прямому назначению; чрезмерная точность модели на практике не менее вредна, чем её неполнота и грубость.
Математическая модель изучаемого процесса или объекта является основой, фундаментом всего исследования. Тем не менее на сегодняшний день не существует и, по-видимому, не может существовать науки о моделировании реальных процессов и явлений окружающего мира – точно так же, как не существует науки о том, как совершать открытия, изобретения, создавать новые методы научного поиска. Даже математика – одна из наук, которая в большей, чем другие науки, степени использует дедукцию, своему прогрессу обязана в громадной степени таким “ненаучным” приемам, как интуиция, догадка, фантазия, т. е. индуктивному способу мышления. Моделирование объектов и явлений реальности (на сегодняшний день) в большой степени представляет искусство, а искусству учат на опыте. Человечество обладает таким опытом. Это опыт классиков естествознания, опыт представителей естественных наук, эксплуатирующих для своих целей математический аппарат, и т. д.
В каждом конкретном случае качество модели во многом зависит от способностей исследователя понять существо, физику изучаемого процесса и создать его адекватное математическое описание. Математику привлекают, когда сложен изучаемый или управляемый процесс. Сложность обычно состоит в огромном числе характеристик, его описывающих, и большом числе связей между ними. И задача заключается не только в том, чтобы создать адекватное математическое описание изучаемого процесса, т. е. его модель, но и разработать методику работы с нею. С громоздкими многопараметрическими моделями трудно проводить исследования, поэтому математики вынуждены были при формализации реального процесса отбрасывать многие, на их взгляд менее существенные связи, загрублять математическое описание. Необходимо обладать незаурядной интуицией для определения, что важно с точки зрения интересующих исследователя вопросов, что – нет. Однако при решении серьезных практических задач невозможно полагаться лишь на интуицию и опыт небольшой группы исследователей, необходима методика, позволяющая с большой степенью достоверности определить адекватность модели и реальности, ею описываемой, область возможного ее применения и круг вопросов, для исследования которых они пригодны. Необходима «система знаний», которая позволила бы, используя накопленный опыт и определенные принципы, выработанные на его основе, а также доказанные или установленные на их базе положения, создавать модели изучаемых процессов, проводить их анализ и определять пути их дальнейшего использования.
ОБ АДЕКВАТНОСТИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Так, возникло понятие «адекватность» и стало необходимым при проверке математических моделей.
Любая математическая модель характеризуется в первую очередь, необходимостью математических вычислений, что повлекло за собой появление вычислительного эксперимента. Во время планирования вычислительного эксперимента задействуют различные методы математического моделирования. Причем от методов, которые употребляются в математической статистике до методов, присущих теории катастроф.
С середины двадцатого века центром математического моделирования становится понятие адекватности.
«Если математика является «чистым порождением ума» (своеобразной «игрой в бисер»), то непонятно, почему мир обязан с ней сообразовываться. Если же она является формой абстрагирования в «аминокислотном» человеческом сознании присущих миру (или возможных в нем при отсутствии запрещающих ограничений) структур и отношений, то возникает вопрос об «адекватности», «изоморфности» математических структур структурам реальности» (Д. Гильберт) [1].
Адекватность математической модели особенно важна в задачах эксплуатации, где непосредственно можно сопоставлять расчетные и фактические значения параметров и проверять правильность модели. По многим причинам теоретические значения некоторых коэффициентов в этих соотношениях существенно отличаются от фактических. Точнее, теоретическая модель оказывается недостаточно хорошей для описания реального объекта.
F-тестом или критерием Фишера (F-критерием, φ*-критерием) — называют любой статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение доверительного интервала [2].
Критерий Фишера является очень удобным в проверке адекватности математических моделей. Удобство использования критерия Фишера состоит в том, что проверку гипотезы можно свести к сравнению с табличным значением. Если рассчитанное значение F-критерия не превышает табличного, то, с соответствующей доверительной вероятностью, модель можно считать адекватной. При превышении табличного значения эту приятную гипотезу приходится отвергать. Этот способ расчета дисперсии адекватности, подходит, если опыты в матрице планирования не дублируются, а информация о дисперсии воспроизводимости извлекается из параллельных опытов в нулевой точке или из предварительных экспериментов.
1) опыты во всех точках плана дублируются одинаковое число раз (равномерное дублирование),
2) число параллельных опытов не одинаково (неравномерное дублирование).
Проверка адекватности математической модели системы (или ее отдельных элементов) осуществляется путем проведения экспериментальных исследований и сопоставления их результатов с результатами аналитических расчетов, выполненных для конкретных условий проведения эксперимента[3].
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель как уже было выше сказано считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
Например, табличное значение критерия со степенями свободы k1=1 и k2=48, Fтабл = 4
Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Пример. По совокупности 25 предприятий торговли изучается зависимость между признаками: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты:
Какой показатель корреляции можно определить по этим данным? Рассчитайте величину этого показателя, на основе этого результата и с помощью F-критерия Фишера сделайте вывод о качестве модели регрессии.
Решение. По этим данным можно определить эмпирическое корреляционное отношение:
Поскольку фактическое значение F > Fтабл, то найденная оценка уравнения регрессии статистически надежна.
Таким образом, доказывается адекватность математической модели.
Такие проверки, несмотря на их трудоемкость, проводятся регулярно и, как правило, дают вполне удовлетворительные результаты, подтверждая пригодность всех моделей для практического использования[4]
Из всего вышесказанного можно сделать вывод, что понятие «адекватность» имеет полное право занять достойное место, среди четких математических определений. Именно с помощью этого понятия можно внести в хаотический мир некоторых математических понятий порядок [1].
Список используемых источников
2. Вяхирев, Р. Российская газовая энциклопедия: учебное пособие/ Р. Вяхирев; ред. Р.И. Вяхирев; Изд-во Большая Российская Энциклопедия, 2004г.
3. Адекватность и точность математических моделей. Верификация результатов моделирования [Электронный ресурс] – Режим доступа: http://studopedia.ru/ 4. F-статистика. Критерий Фишера [Электронный ресурс] – Режим доступа: http://math.semestr.ru/corel/fisher.php
В рамках реализации «Государственной молодежной политики Российской Федерации на период до 2025 года» и направления «Вовлечение молодежи в инновационную деятельность и научно-техническое творчество» коллективами преподавателей различных вузов России в 2009 году было предложено совместное проведение электронной научной конференции «Международный студенческий научный форум».
Понятие модели и моделирования
1.4. Адекватность модели
Итак, мы установили: модель предназначена для замены оригинала при исследованиях, которым подвергать оригинал нельзя или нецелесообразно. Но замена оригинала моделью возможна, если они в достаточной степени похожи или адекватны.
Говорят, что модель адекватна оригиналу, если при ее интерпретации возникает «портрет», в высокой степени сходный с оригиналом.
До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему (то есть адекватна ли она), ценность модели нулевая!
Термин » адекватность » как видно носит весьма расплывчатый смысл. Понятно, что результативность моделирования значительно возрастет, если при построении модели и переносе результатов с модели на систему-оригинал может воспользоваться некоторой теорией, уточняющей идею подобия, связанную с используемой процедурой моделирования.
К сожалению теории, позволяющей оценить адекватность математической модели и моделируемой системы нет, в отличие от хорошо разработанной теории подобия явлений одной и той же физической природы.
Если изучение системы проведено качественно и концептуальная модель достаточно точно отражает реальное положение дел, то далее перед разработчиками стоит лишь проблема эквивалентного преобразования одного описания в другое.
Итак, можно говорить об адекватности модели в любой ее форме и оригинала, если:
Предварительно исходный вариант математической модели подвергается следующим проверкам:
Такая предварительная оценка адекватности модели позволяет выявить в ней наиболее грубые ошибки.
Но все эти рекомендации носят неформальный, рекомендательный характер. Формальных методов оценки адекватности не существует! Поэтому, в основном, качество модели (и в первую очередь степень ее адекватности системе) зависит от опыта, интуиции, эрудиции разработчика модели и других субъективных факторов.
Две системы изоморфны, если существует взаимно однозначное соответствие между элементами и отношениями (связями) этих систем.
При моделировании сложных систем достигнуть такого полного соответствия трудно, да и нецелесообразно. При моделировании абсолютное подобие не имеет места. Стремятся лишь к тому, чтобы модель достаточно хорошо отражала исследуемую сторону функционирования объекта. Модель по сложности может стать аналогичной исследуемой системе и никакого упрощения исследования не будет.
Для оценки подобия в поведении (функционировании) систем существует понятие изофункционализма.
1.5. Требования, предъявляемые к моделям
Итак, общие требования к моделям.
Эти требования (обычно их называют внешними) выполнимы при условии обладания моделью внутренними свойствами.
Модель должна быть:
В заключение темы сделаем несколько замечаний. Трудно ограничить область применения математического моделирования. При изучении и создании промышленных и военных систем практически всегда можно определить цели, ограничения и предусмотреть, чтобы конструкция или процесс подчинялись естественным, техническим и (или) экономическим законам.
Критерии адекватности математической модели и объекта
АДЕКВАТНОСТЬ МОДЕЛИ — соответствие модели моделируемому объекту или процессу. Адекватность — в какой-то мере условное понятие, так как полного соответствия модели реальному объекту быть не может, иначе это была бы не модель, а сам объект. При моделировании имеется в виду адекватность не вообще, а по тем свойствам модели, которые для исследования считаются существенными.
Модель считается адекватной, если отражает заданные свойства с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта.
Точность математической модели оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели.
Верификация — проверка, проверяемость, способ подтверждения каких-либо теоретических положений, алгоритмов, программ и процедур путем их сопоставления с опытными (эталонными или эмпирическими) данными, алгоритмами и программами.
Верификация — это подтверждение соответствия конечного продукта Проверка истинности теоретических положений, установление их достоверности предопределённым эталонным требованиям логико-методологическая процедура установления истинности научной на основе их соответствия эмпирическим данным или теоретическим положениям, соответствующим эмпирическим данным. В рамках логического позитивизма принцип верифицируемости мыслится критериально исчерпывающим способом апробации научных утверждений, понятых в качестве «протокольных предположений» как фиксаций данных непосредственного опыта: утверждения, выходящие за рамки «протокольных предложений» трактуются как неверифицируемые, в случае чего в действие вступает принцип фальсифицируемости.
Модель и понятие моделирования.
Модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.
Моделирование – процесс создания и использования модели.
Проектирование и управление
Прогнозирование поведения объектов
Тренировка и обучения специалистов
Классификация по форме представления
a) геометрически подобные масштабные, воспроизводящие пространственно- геометрические характеристики оригинала безотносительно его субстрату (макеты зданий и сооружений, учебные муляжи и др.);
b) основанные на теории подобия субстратно подобные, воспроизводящие с масштабированием в пространстве и времени свойства и характеристики оригинала той же природы, что и модель, (гидродинамические модели судов, продувочные модели летательных аппаратов);
c) аналоговые приборные, воспроизводящие исследуемые свойства и характеристики объекта оригинала в моделирующем объекте другой природы на основе некоторой системы прямых аналогий (разновидности электронного аналогового моделирования).
Идеальные – материальная точка, абсолютно твердое тело, математический маятник, идеальный газ, бесконечность, геометрическая точка и прочее.
3.2. Частично формализованные.
3.3. Вполне формализованные (математические) модели.
Конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;
Упрощенность: модель отображает только существенные стороны объекта;
Приблизительность: действительность отображается моделью грубо или приблизительно;
Адекватность: насколько успешно модель описывает моделируемую систему;
Потенциальность: предсказуемость модели и её свойств;
Сложность: удобство её использования;
Полнота: учтены все необходимые свойства;
Цели и задачи моделирования.
Цели и задачи компьютерного моделирования.
Главной задачей компьютерного моделирования выступает построение информационной модели объекта, явления.
1) Познание окружающего мира.
Зачем человек создает модели? Несколько миллионов лет назад первобытные люди изучали окружающую природу, чтобы научиться противостоять природным стихиям, пользоваться природными благами, просто выживать. Накопленные знания передавались из поколения в поколение устно, позже письменно, наконец, с помощью предметных моделей. Так родилась, к примеру, модель земного шара — глобус, — позволяющая получить наглядное представление о форме нашей планеты, ее вращении вокруг собственной оси и расположении материков. Такие модели позволяют понять, как устроен конкретный объект, узнать его основные свойства, установить законы его развития и взаимодействия с окружающим миром моделей.
2) Создание объектов с заданными свойствами (задача типа «Как сделать, чтобы. »).
Накопив достаточно знаний, человек задал себе вопрос: «Нельзя ли создать объект с заданными свойствами и возможностями, чтобы противодействовать стихиям или ставить себе на службу природные явления?» Человек стал строить модели еще не существующих объектов. Так родились идеи создания ветряных мельниц, различных механизмов, даже обыкновенного зонтика. Многие из этих моделей стали в настоящее время реальностью. Это объекты, созданные руками человека.
3) Определение последствий воздействия на объект и принятие правильного решения (задача типа «Что будет, если. »: что будет, если увеличить плату за проезд в транспорте, или что произойдет, если закопать ядерные отходы в такой-то местности?)
Например, для спасения Петербурга от постоянных наводнений, приносящих огромный ущерб, решено было возвести дамбу. При ее проектировании было построено множество моделей, в том числе и натурных, именно для того, чтобы предсказать последствия вмешательства в природу.
4) Эффективность управления объектом (или процессом).
Поскольку критерии управления бывают весьма противоречивыми, то эффективным оно окажется только при условии, если будут «и волки сыты, и овцы целы». Например, нужно наладить питание в школьной столовой. С одной стороны, оно должно отвечать возрастным требованиям (калорийное, содержащее витамины и минеральные соли), с другой — нравиться большинству ребят и к тому же быть «по карману» родителям, а с третьей — технология приготовления должна соответствовать возможностям школьных столовых. Как совместить несовместимое? Построение модели поможет найти приемлемое решение.
Классификация моделей.
1. Классификация по области использования
Учебные: наглядные пособия, различные тренажеры, обучающие программы.
Опытные: уменьшенные или увеличенные копии исследуемого объекта для дальнейшего его изучения (модели корабля, автомобиля, самолета, гидростанции).
Игровые: военные, экономические, спортивные, деловые игры.
Имитационные: отражают реальность с той или иной степенью точности (испытание нового лекарственного средства в ряде опытах на мышах; эксперименты по внедрению в производство новой технологии).
2. Классификация с учетом фактора времени
Динамическая модель позволяет увидеть изменения объекта во времени
3. Классификация по способу представления
Любая информационная модель содержит лишь существенные сведения об объекте с учетом той цели, для которой она создается. Информационные модели одного и того же объекта, предназначенные для разных целей, могут быть совершенно разными.
Дата добавления: 2018-02-18 ; просмотров: 4540 ; Мы поможем в написании вашей работы!
Адекватность и универсальность математической модели
Реалистичное поведение имитируемой модели увеличивает эффективность имитатора за счет увеличения реалистичности поведения модели. Дело в том, что правдоподобное поведение модели увеличивает так называемый эффект личного участия (ощущается меньшая разница между реальной и виртуальной обстановкой). Эффект личного участия, в свою очередь, влияет на запоминание информации. Возможность изучения влияния большего числа параметров представляет важный исследовательский интерес, так как при работе с реальным оборудованием нередко возникают ситуации, изменяющие условия его работы. Примерами могут служить изменение состояния атмосферного воздуха (температура, давление, влажность и т.д.), различные характеристики оборудование, его износ и т.д.
Реалистичное поведение имитируемой модели целиком и полностью зависит от качества реализации математической модели. Под математической моделью понимается система математических соотношений, описывающих с требуемой точностью изучаемый объект и его поведение (что и определяет соответствие поведения реальной системы и поведения модели). При построении математических моделей используют различные математические средства описания объекта: теорию множеств, теорию графов, теорию вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения, метод конечных элементов и т. д.
Реалистичное поведение имитируемой модели зависит от адекватности и универсальности используемой математической модели. Под адекватностью понимается способность модели отражать заданные свойства объекта с приемлемой точностью. Универсальность модели определяется количеством параметров, учитываемых в процессе имитации. По этой причине, при создании имитатора, обязательно определяются требования к создаваемой математической модели. В техническом задании обязательно должны быть указаны необходимая точность модели (адекватность), требуемый интервал входных значений, на котором эта точность должна быть выдержана (область адекватности), и количество учитываемых входных данных (универсальность). Кроме того, в обязательном порядке должны быть указаны параметры компьютера (компьютеров), на котором должен выполнятся тренажер, это в свою очередь определяет лимит использования вычислительных ресурсов для реализации имитационной модели. На практике требования к высокой адекватности и универсальности модели, как правило, ограничиваются доступными вычислительными ресурсами, что требует нахождения наилучшего компромиссного решения.
Для формализации этого процесса необходимо ввести целевую функцию, определяющую качество математической модели целом:
Из представленного выражения следует:
Определение (заказчиком) ограничений на значения факторов и их «вес» позволяет формализовать процесс контроля качества создаваемой модели на всех этапах. Методики оценки адекватности, универсальности и экономичности модели подробно описаны в следующих разделах.
Требования к адекватности
При создании математической модели КИТ очень важно добиться требуемого соответствия между поведением реальной системы и поведением модели. Для формализации оценки этого соответствия необходим механизм определения адекватности модели.
Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью (точность определяется как степень совпадения значений выходных величин модели и объекта). В настоящее время применяются следующие способы определения адекватности:
Достоинства метода: не требует наличия метрического пакета, нет необходимости в проведении замеров (эксперимента), статистической обработки и т. д. Недостатки метода: субъективность оценки, значительная зависимость точности оценки от компетенции экспертов, большой риск обнаружения ошибок во время эксплуатации тренажера.
Результат расчета на основе корреляционных зависимостей, при наличии «очень похожих» моделей и их аппроксимаций или расчетов с помощью МКЭ (например COMSOL).
Результат определения с помощью общих теорий на основе принятых допущений и аксиом (сравнение с данными «хорошо» себя зарекомендовавшей «похожей» модели). Хорошо подходит для математических моделей, построенных на основе широко известных законов (закон Ома, Кирхгофа, Ньютона и т.д.).
Достоинства метода: объективность оценки. Недостатки метода: значительная зависимость от достоверности теоретического аппарата, высокая сложность при многофакторном анализе.
Для всех способов определения адекватности, кроме экспертного, необходима статистическая обработка данных, полученных с помощью модели и «эталонных» данных.
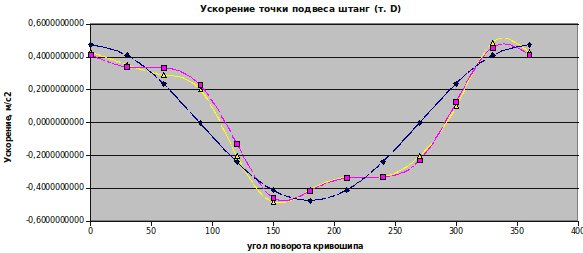
Например, математическую модель кинематики станка качалки можно проверить с использованием сразу трех теорий кинематики СК — упрощенной, уточненной и точной.
Рисунок. Диаграмма скорости точки подвеса штанг от угла поворота кривошипа
Точность модели может изменятся, в зависимости от условий функционирования объекта, обусловленных разными внешними воздействиями (нагрузками, температурой внешней среды и др.) на моделируемый объект. Если задаться предельной допустимой погрешностью εпр, то в пространстве возможных изменений внешних воздействий на объект для принятых m условий его функционирования можно выделить область, в которой выполняется условие εм
Требования к экономичности модели
Реализация математической модели требует определенных вычислительных ресурсов, определяемых количеством машинного времени ТМ и объемом оперативной памяти ПМ, необходимой для реализации модели. В качестве меры обычно используется FLOPS (Floating point Operations Per Second) — величина, используемая для измерения производительности компьютеров, показывающая, сколько операций с плавающей запятой в секунду выполняет данная вычислительная система. Значение FLOPS, как отдельного компьютера, так и компьютерного кластера, можно рассчитать при помощи теста LINPACK, который основывается на решении определенного набора систем линейных алгебраических уравнений. Результат выполнения теста показывает значение производительности компьютера в FLOPS. В данной работе используется реализация теста LINPACK от Intel, доступная для скачивания по адресу http://software.intel.com/en-us/articles/intel-math-kernel-library-linpack-download/, http://ubuntuforums.org/showthread.php?t=1004406).
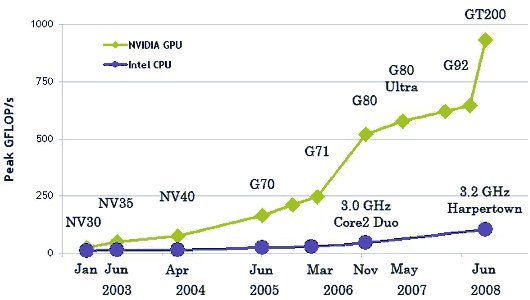
В настоящее время наблюдается рост производительности как центральных, так и графических процессоров. Имеется тенденция переноса вычислений с центрального процессора на графический в силу значительно больших возможностей последних. Возможность переноса вычислений на графические процессоры также необходимо учитывать (для этого существуют специальные реализации теста LINPACK).
Рисунок. Увеличение GFLOPS\s центральных процессоров и GPU
Исследования наиболее распространенных в настоящее время компьютеров и кластеров приведены в таблице ниже. Часть данных была экспериментально получена автором, остальные данные извлечены из официальных источников.
Таблица. Оценка производительности по тесту LINPACK различных процессоров и гибридных кластерных систем
| Процессор | OS | GFlops\s |
|---|---|---|
| Intel(R) Core(TM)2 Duo CPU E8400 @ 3.00GHz | GNU/Linux Ubuntu 9.10 x86_64 | 21,48 |
| Pentium ® Dual-core CPU T4300 @ 2.10GHz | GNU/Linux Ubuntu 9.10 x86_64 | 5,39 |
| Intel Core i7 860 2.80 GHz (Lynnfield) | GNU/Linux Ubuntu 9.10 x86_64 | 52,79 |
| Celeron 1.200 GHz | 2,09 | |
| dualcore atom 330 | GNU/Linux Ubuntu 7.10 | 0,74 |
| 2 x Xeon X5365 3 GHz | GNU/Linux Ubuntu 9.10 x86_64 | 58,84 |
| intel q9550 3.604 GHz | GNU/Linux Ubuntu 7.10 | 50,04 |
| Nvidia Geforce GTX280 | По материалам Nvidia | 75 |
| IBM xSeries 335 cluster (dual 3.06 Xeon w/InfiniBand) | По материалам IBM | 1389 |
Соответственно экономичность (C) определяется уравнением: