Чем описывается состояние микрочастиц в квантовой механике

Определение состояния микрочастицы в квантовой механике. Волновая функция

Для классической частицы ее состояние в любой момент вре­мени задается координатой частицы x(t) и ее скоростью v(t) = dx/dt (в простейшем случае одномерного движения вдоль оси X). Такое определение состояния в квантовой механике не имеет никакого смысла из-за соотношения неопределенностей.

Данная ситуация связана с наличием у микрочастиц волновых свойств. В частности, одинаковые дифракционные картины при распространении волн и движении микрочастиц позволяют допустить, что и поведение микрочастиц описывается неким волновым уравнением.

Разложение волновой функции в ряд Фурье дает все возможные результаты измерения импульса частицы. Вероятность каж­дого из этих результатов определяется квадратом соответствующе­го коэффициента разложения Фурье. При этом каждое новое измерение координат и импульса частицы изменяет существовавшее до него распределение вероятностей.

Уравнение Шредингера

По определению квантового состояния уравнение движения квантовой частицы должно задавать изменения во времени вол­новой функции ψ. Такое уравнение впервые было предложено Э.Шредингером в 1926 г, и названо его именем. Обратим внимание на то, что уравнение Шредингера (как и уравнение Ньютона) не выводится, а постулируется. В простом случае, когда ψ-функция не зависит от времени, уравнение называется стационарным и имеет следующий вид:

— оператор Лапласа (лапласиан).

В общее (или временное) уравнение Шредингера входит также производная dψ/dt, отражающая изменение волновой функции времени.

Источник

КВАНТОВАЯ МЕХАНИКА, СОСТОЯНИЕ МИКРОЧАСТИЦЫ

СОДЕРЖАНИЕ

19. Строение вещества. Общие вопросы…………………………………42

20. Эквивалентность одинаковых частиц………………………………. 43

21. Геометрические свойства молекул……………………………………46

22. Электрические свойства молекул. Дипольный

23. Электронные, колебательные и вращательные состояния

Решение.

а)

б) ;

в) .

9. Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой b=1 мкм. Определить скорость этих электронов, если известно, что на экране, отстоящем от щели на расстоянии l=0,5 м, ширина центрального дифракционного максимума Dх=0,8 мм.

Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью, ширина которой b=0,1 мкм. Определить скорость этих электронов, если известно, что на экране, отстоящем от щели на расстояние 0,5 м, ширина центрального дифракционного максимума Δ=0,8 мм.

Неопределённость в координате электрона Δx₀

b. В соответствии с соотношением неопределённости для координаты и одноимённой проекции импульса имеем: Δp_x

Из рисунка видно, что

Подставляя сюда числовые данные, получим:

Ответ: n=hl/mbDх 0,9×10 4 км/с.

10. Параллельный поток электронов, ускоренных разностью потенциалов V=25 в, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d=50 мкм. Определить расстояние между соседними максимумами интерференционной картины на экране, расположенной на расстоянии l=1 м от щелей.

Ответ: hl/2dÖ2meV@2,5 мкм.

11. Проходя через отверстие, электроны попадают на один из трех участков экрана: А, В, или С. На участок В они попадают чаще, чем на участки А или С. Вы собираетесь пропустить через отверстие очередной электрон. Ответьте на вопросы:

1. Можно ли предсказать, куда попадет электрон?

12. Сформулируйте постулат о состоянии квантовой системы. Что такое волновая функция? От чего она зависит?

13. Почему волновые свойства частиц обнаружены в явлениях атомного масштаба? Можно ли в рамках квантовой теории описывать движения макротел? Вселенной?

14. Что означают координаты x, y, z в волновой функции y (х, y, z). Чем эти координаты отличаются от координат частицы в макромире?

15. Как в квантовой механике понимается классическое выражение “Частица движется”?

16. Волновая функция позволяет получить полную информацию о квантовой системе. Что это значит?

17. Может ли квантовая частица покоиться? Почему?

18. Обязательно ли использование y-функции в аппарате квантовой механики? Всегда ли y-функции имеют математический вид волн? Приведите примеры, подтверждающие Ваши утверждения.

19. Каким условиям должна удовлетворять волновая функция частицы? Какой физический смысл имеют стандартные условия: непрерывности, однозначности, ортогональности, нормированности y?

20. Какой физический смысл можно увидеть в том, что y-функция свободной частицы не нормируется обычным образом? Какой физический смысл в нормировке волн Де Бройля по Борну?

21. Сформулируйте принцип суперпозиции полей, волн, сил и т.д.

23. Может ли функция erбыть волновой функцией? А функция eir? Почему? Может ли функция аrcsin x быть волновой функцией?

25. Какое выражение характеризует плотность вероятности найти частицу с координатами x, y, z?

26. Чем отличается плотность вероятности от вероятности? Какова вероятность найти частицу в точке x₀, y₀, z₀? А плотность вероятности?

27. Какие эксперименты указывают на невозможность классического описания движения микрочастицы?

28. Состояние микрочастицы характеризуется волновой функцией

Y = А exp px.

Какая из следующих функций (1, 2) описывает другое состояние частицы?

29. Для чего введен принцип суперпозиции состояний в квантовой механике?

30. Какой математический смысл имеет утверждение, что умножение волновой функции на любую постоянную С не меняет состояние системы?

31. Будет ли суперпозиция двух разных волн Де Бройля описывать состояние с определенным импульсом и энергией?

ОПЕРАТОРЫ

32. Почему математический аппарат квантовой механики использует операторы? Что называется оператором? Сформулируйте постулат об операторах.

33. Почему операторы квантовой механики должны быть линейными?

34. Проверьте, линейны ли операторы :

а) d/dx; б) id/dx; в) x+d/dx; г) ;

д) оператор комплексного сопряжения; е) .

35. Почему операторы квантовой механики должны быть эрмитовыми?

36. Проверьте, являются ли эрмитовыми операторы:

а) d/dx; б) id/dx; в) 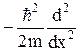; г) ;

д) 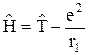, где .

Решение. В каждом из случаев а-д необходимо проверить условие эрмитовости оператора:

.

б)

37. Найти операторы:

a) ; б) ; в) .

Решение. Чтобы получить сложный оператор или выполнить действия с ним, необходимо подействовать оператором на волновую функцию, произвести действия, а в результате волновую функцию отбросить.

а) =

= =

.

.

38. Подействуйте оператором на функцию:

Решение.

=

.

39. Найдите операторы и :

а) в сферической системе координат;

б) в цилиндрической системе координат.

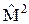
40. Оператор квадрата углового момента в сферической системе координат имеет вид: . Запишите оператор в явном виде и подействуйте оператором на следующие функции :

а) ; б) ; в) .

41. Найдите операторы, переводящие одни функции в другие:

а) ;

б) ;

в) .

Решение.

в) Разложим в ряд в точке .

,

где .

Учтем, что ; тогда , где е, возведенная в степень оператора, подразумевает разложение степени в ряд.

42. Найдите коммутаторы:

а) ; б) ; в) ; г) .

43. Покажите, что коммутатор .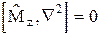

44. Коммутирует ли гамильтониан частицы с оператором импульса, оператором потенциальной энергии?

Решение.

,

60. Электрон с кинетической энергией Т = 10 Эв локализован в области размером l = 1 мкм. Оценить относительную неопределенность скорости электрона.

61. Оценить минимальную энергию Е_min гармонического осциллятора, имеющего массу m (потенциал U=kx 2 /2, частота w=(k/m) 1/2 ), используя соотношение неопределенности.

62. Оценить с помощью соотношения неопределенности энергию связи электрона в основном состоянии атома водорода и соответствующее расстояние электрона до ядра.

Решение. Энергия электрона Е = .

Е @ .

Найдем min этого выражения: (¶Е/¶r) = 0.

; r_min = =a=0,529 — радиус первой Боровской орбиты.

63. Оценить минимальную возможную энергию электронов в атоме Не и соответствующее расстояние от электрона до ядра.

.

Примечание:

Минимальная возможная энергия электрона будет тогда, когда минимальна энергия кулоновского отталкивания электронов, т.е. когда электроны атома будут находиться на максимально возможном расстоянии друг от друга. Эта энергия отталкивания соответствует оценке

.

Для полной энергии электронов, поэтому справедлива оценка.

Е(r₁; r₂) =

13,6 эВ,

где величина 13,6эВ= постоянная Ридберга. Так как Z=2,то

Решение. Dх

сt = 3 м; (Dl/l) = сt/l; DЕDt = hct/Dl ³ h; Dl £ сt.

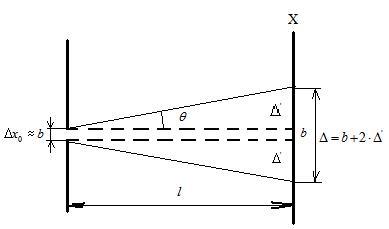
65. Монохроматический параллельный пучок электронов нормально падает на диафрагму с энергией Е=100 Эв, в которой узкая щель (рис. 5). На расстоянии L=100 см от диафрагмы расположен экран. Оцените ширину щели, при которой ширина изображения на экране будет минимальной.

p = ; Dр » h/b,

D¢ = Lq = L ,

D = D¢ + b = b + » 2b = 8,8 мкм,

D’

66. Проверьте принцип неопределенности на примере основного состояния электрона в одномерной прямоугольной яме с бесконечно высокими стенками.

68. Какая возникает неопределенность в энергии частицы массой m при ее локализации в области размером l см?

69. Частица массой m движется в одномерной прямоугольной яме шириной l с бесконечно высокими стенками. Неопределенность в координате частицы Dх = l, импульс же частицы известен точно из ее полной энергии. Не противоречит ли это неравенству Гейзенберга?

70. Не противоречит ли принципу неопределенности состояние электрона в атоме с нулевым моментом количества движения?

Указание. Чтобы ответить на вопрос, запишите выражение для оператора кинетической энергии электрона, движущегося в поле центральных сил, в сферической системе координат.

71. Оцените величину кулоновского отталкивания электронов в атоме Не.

72. Два атома водорода сближаются из бесконечности на конечное расстояние. Как изменяются уровни энергии в системе?

ФУНКЦИИ ОПЕРАТОРОВ

75. Найдите собственные функции операторов:

а) ; б) .

77. Покажите, что две разные собственные функции эрмитовского оператора ортогональны.

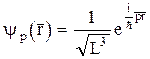
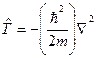
78. Покажите, что волна де Бройля является собственной функцией оператора кинетической энергии частицы .

79. Покажите, что волны де Бройля и ортогональны, но относятся к одному и тому же собственному значению . Каков физический смысл вырождения состояний оператора кинетической энергии?

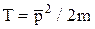
80. Эрмитовский оператор задан в виде матрицы . Определите собственные значения и собственные функции оператора .

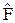
81. Покажите, что если оператор симметрии системы 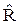оставляет неизменным гамильтониан, то состояния системы вырождены.

82. Какой физический смысл имеет ортогональность собственных функций оператора? А нормированость?

83. В чём состоит физический смысл вырождения собственных функций оператора ?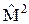

5. УРАВНЕНИЕ ШРЕДИНГЕРА.
ИЗМЕНЕНИЕ СОСТОЯНИЯ СО ВРЕМЕНЕМ

84. Чем отличается уравнение Шредингера от уравнения диффузии?

86. Что называется полным набором величин? Сколько величин входит в полный набор?

87. Чем отличается полный набор величин в квантовой механике от полного набора величин в классической механике?

88. Что такое интеграл движения? Какая разница в истолковании интегралов движения в квантовой и классической механике?

89. Что понимают под стационарным состоянием в квантовой механике? Чем это толкование отличается от классического?

90. Если стационарное состояние в квантовой механике меняется со временем, почему оно называется стационарным?

91. Как стационарное квантовое состояние зависит от времени?

92. Выясните зависимость от времени средней величины не зависящего от времени оператора , если состояние частицы:

93. Запишите уравнение Шредингера в энергетическом представлении.

95. Запишите гамильтониан для следующих микросистем:

а) Li, б) Be, в) Li₂, г) , е) Н₂О.

96. Покажите, что точный гамильтониан молекул изомеров одинаков.

96а. Почему гамильтонианы молекул изомеров, написанные в адиабатическом приближении, различаются?

97. Покажите, что:

а) точный гамильтониан молекулы не меняется при перестановке любой пары частиц молекулы;

б) точный гамильтониан левой и правой частей уравнения химической реакции одинаков.

97а. Покажите, что гамильтонианы молекул изомеров, написанные в адиабатическом приближении, изменяются при перестановке различных ядер.

98. Покажите, что из уравнения Шредингера следует закон сохранения массы.

99. Покажите, что из уравнения Шредингера следует закон сохранения электрического заряда.

100. Что в квантовой механике называют:

а) потенциальной ямой?

б) потенциальным барьером?

в) потенциальной стенкой?

101. Напишите уравнение Шредингера для стационарных состояний частицы, имеющей энергию Е и движущейся в потенциале вида (рис. 6).

Решение.

в) 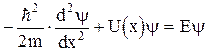, где U(x) = U₀, при x а;

г) при том же уравнении U(x) = U₀, при x 2(b + R);

U(x) = 0, при 0 £ х £ b; b + 2R £ х £ 2(b + R);

150. Найдите частоту перехода электрона в атоме водорода между

ТЕОРИЯ ВОЗМУЩЕНИЙ

151. Что понимают под оператором возмущения?

152. В каком смысле говорят о необходимости малости возмущения?

153. Чему равна поправка к энергии системы в первом и во втором приближениях теории возмущений?

154. Состояние некоторой системы описывается волновыми функциями y₁, y₂, y₃, y₄, и соответствующими собственными значениями Е₁=1, Е₂=2, Е₃=3, Е₄=4. Матричные элементы оператора возмущения равны: W₁₁=0,4; W₂₂=0,3; W₃₃=0,2; W₄₄=0,1; W₁₂=W₁₃=0,1; W₂₃=0,2; W₁₄=W₂₄=0.

а) поправки к уровням энергии в первом и во втором приближениях теории возмущений;

б) поправки первого приближения к волновым функциям;

в) точные собственные значения возмущенной задачи;

г) нормированные волновые функции в первом приближении теории возмущений.

МЕТОД ХАРТРИ

185. В чем сущность метода Хартри? Запишите оператор потенциальной энергии i-го электрона в методе Хартри. Запишите его на примере первого электрона атома Ве.

186. Запишите уравнение Шредингера для молекулы Li₂ в приближении Хартри (а также Ве₂, ).

187. Почему уравнение Хартри является нелинейным? Проверьте, является ли оператор Гамильтона, записанный в приближении Хартри, линейным?

188. В чем смысл метода самосогласованного поля? Что понимается под самосогласованным полем? Самосогласованной орбиталью?

190. Будет ли полная электронная энергия в методе Хартри равна сумме энергий занятых орбиталей? Почему?

Источник