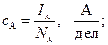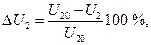Чем ограничивается применение метода непосредственной нагрузки
Испытание трансформатора методом непосредственной нагрузки
Метод позволяет опытным путем снять внешнюю характеристику трансформатора.
Внешняя характеристика — это зависимость U2 = f(I2), где U2 —напряжение на зажимах вторичной обмотки трансформатора; I2 — ток нагрузки при частоте сети f = 50 Гц и коэффициенте мощности cos j2 — const.
Внешняя характеристика также может быть выражена зависимостью напряжения U2 от коэффициента нагрузки b при тех же условиях, где
В этом же опыте определяют КПД трансформатора и изменение напряжения DU2.
Электрическая схема для проведения испытаний трансформатора приведена на рис. 7.1. Питание лабораторной установки производится от сети переменного тока напряжением 220 В, а для изменения напряжения, подводимого к первичной обмотке трансформатора, используют универсальный источник питания ИП (блок 60-105).
Блок 60-105 автоматически отключается в случае перегрузки по току. На источнике питания имеется кнопка «Аварийное отключение» для экстренного отключения питания в случае непредвиденных обстоятельств.
Рис. 7.1. Принципиальная электрическая схема для проведения опытов холостого хода и непосредственной нагрузки трансформатора
Однофазный трансформатор номинальной мощностью Sном = 100 В·А размещен в блоке 61-106. Предусмотрена возможность использования другого трансформатора мощностью Sном = 1000 В·А.
Измерение токов и напряжений в первичной и вторичной обмотках трансформатора производят с использованием измерительных блоков 68-117 с многопредельными амперметром и вольтметром в каждом из них. Из имеющихся пределов измерений приборов: амперметра — 1 А, 5 А, 10 А, вольтметра — 50 В, 250 В, 500 В следует выбрать необходимые значения для первичной и вторичной цепей трансформатора.
Измерение токов и напряжений можно также осуществлять виртуальной измерительной системой 68-500 с использованием программного обеспечения 65-500-USВ. Можно воспользоваться и универсальным измерительным блоком 68-100 для измерения токов, напряжений, активной и реактивной мощностей.
Измерение мощности Р1 электрической энергии, потребляемой трансформатором из сети, производят измерительным блоком 68-200. Следует иметь в виду, что пределы измерений тока в первичной обмотке трансформатора в режиме холостого хода и в режиме номинальной нагрузки различаются примерно на порядок. Поэтому при проведении измерений необходимо внимательно следить за пределом тока Iw на переключателе блока 68-200 измерения мощности.
Ток Iw переключателя ваттметра в режиме номинальной нагрузки трансформатора выбирают таким, чтобы он был близок к I1ном, а в режиме холостого хода Iхх = I0 ≈ Iw ≈ 0,1I1ном.
Учитывая, что ток Iw = I1, цены делений сА, сW амперметра и ваттметра можно определить по формулам:
где IА — ток переключателя амперметра в измерительном блоке 68-117; Iw и Uw — ток и напряжение переключателей выбора пределов в измерительном блоке 68-200; NA и Nw — число делений амперметра и ваттметра, соответственно.
Цена деления вольтметра блока 68-117 вычисляется по формуле:
где U — предел измерения напряжения вольтметра блока 68-117;
Nv — число делений вольтметра.
Испытание трансформатора проводят при активной нагрузке, т.е. при cos j2 = 1. Для трансформатора с Sном = 100 В·А нагрузкой является резистивный блок 67-142, а с Sном = 1000 В·А — используют нагрузочный реостат с допустимым током 5…7 А.
Опыт непосредственной нагрузки проводят в следующей последовательности.
1. Устанавливают токи I1 и Iw переключателей на блоках 68-117 и 68-200, значения которых должны быть приблизительно равны номинальному току I1ном первичной обмотки исследуемого трансформатора.
2. Выключателем S1 включают источник питания — блок 60-105. С помощью регулятора напряжения блока 60-105 устанавливают напряжение U1 = U1ном и в течение всего опыта поддерживают его неизменным.
3. Изменяют ток нагрузки I2 от холостого хода (I2 = 0) до номинального так, чтобы I2 принимал значения, близкие к (0,2; 0,4; 0,6; 0,8; 1,0) I2ном.,
4. Измеряют напряжение U2 на зажимах вторичной обмотки трансформатора, токи I1 и I2 в первичной и вторичной обмотках и активную мощность Р1 электрической энергии, потребляемой трансформатором из сети. Результаты измерений заносят в табл. 7.1.
Характеристики трансформатора при U1ном = 220 В; cos j2 = 1; f = 50 Гц
| Опытные данные | Результаты вычислений | Примечания | |||||
| I1, А | P1, Вт | U2, В | I2 | b | cos j1 | P2, Вт | h |
| сv =…В/дел; сA =…A/дел; сw =…Вт/дел. |
5. Для каждого из измеренных токов I2 вычисляют значения следующих величин:
β — коэффициент нагрузки; cos j1— коэффициент мощности; Р2 — мощность нагрузки; η— КПД трансформатора,
где 

6. По данным измерений и вычислений строят внешнюю характеристику U2 = f(b) трансформатора и зависимость h = f(b), как показано на рис. 7.2. Подобные характеристики могут быть построены и в абсолютных единицах в зависимости от тока I2. По зависимости h = f(b) определяют коэффициент нагрузки b, при котором КПД трансформатора имеет максимальное значение.
Рис. 7.2. Характеристики трансформатора
7. Определяют коэффициент трансформации n, который примерно равен:
где U1ном — номинальное напряжение первичной обмотки,U20 — вторичное напряжение при холостом ходе трансформатора, т.е. при I2 = 0.
8. Вычисляют относительное значение изменения напряжения на зажимах вторичной обмотки трансформатора в процентах:
где 

Дата добавления: 2015-04-16 ; просмотров: 32 ; Нарушение авторских прав
Метод непосредственной нагрузки электрических машин и трансформаторов без отдачи энергии в сеть
Электрические машины и трансформаторы под нагрузкой испытывают на нагревание, надежность, а также для определения их энергетических характеристик, при настройке коммутации и ее проверке в машинах постоянного тока и коллекторных машинах переменного тока. В соответствии с ГОСТ 25000—81 при испытаниях используются методы непосредственной или косвенной нагрузки. При методе непосредственной нагрузки испытания проводятся в номинальном режиме работы, который не отличается от работы в реальных условиях. Метод непосредственной нагрузки может быть реализован тремя способами: без отдачи и с отдачей энергии в сеть, а также путем взаимной нагрузки.
В качестве нагрузки трансформаторов и электрических машин, работающих в режиме генератора, используются проволочные, жидкостные или ламповые нагрузочные реостаты. В этом случае вся отдаваемая ими электрическая энергия поглощается в нагрузочных реостатах. Регулирование нагрузки осуществляется путем изменения сопротивления нагрузочных реостатов или путем регулирования напряжения генераторов. Испытания в этом режиме проводятся либо для генераторов и трансформаторов небольшой мощности (до 10 кВ А), либо для генераторов специальных типов, которые не могут работать совместно с электрическими двигателями. Нагрузка трансформаторов с масляным охлаждением может осуществляться и в режиме короткого замыкания так, чтобы потери в его обмотках были равны сумме номинальных потерь короткого замыкания и холостого хода.
Нагрузочные реостаты могут быть регулируемыми или нерегулируемыми. Отметим, что нецелесообразно использовать жидкостные реостаты на постоянном токе из-за электролиза жидкости, оседания на контактах продуктов электролиза и разъедания контактных поверхностей. Что касается индуктивной нагрузки, то ее можно обеспечить с помощью регулируемых реакторов или машин переменного тока, работающих в режиме холостого хода. В зависимости от мощности нагрузки может применяться естественное воздушное, форсированное воздушное или жидкостное охлаждение нагрузочных устройств.
Нагрузка электрических машин, работающих в режиме двигателя, осуществляется в этом случае с помощью тормозов различного типа.
Реализация этого метода требует, как правило, многократного преобразования энергии и сложного комплекта испытательного оборудования. Поэтому его применение экономически оправдано при испытаниях электрических машин средней и большой мощности.
Рассмотрим использование метода непосредственной нагрузки с возвратом энергии в сеть применительно к электрическим машинам различного типа.
Машины постоянного тока. При испытаниях двигателя постоянного тока его питание осуществляется либо от сети постоянного тока, либо от управляемого выпрямителя. Нагрузкой испытуемого двигателя ИД (рис. 1, я) является электромашинный тормоз, в качестве которого используется генератор постоянного тока с независимым возбуждением ГПТ. К генератору ГП1 подключен якорь двигателя постоянного тока с независимым возбуждением ДПТ по так называемой схеме «генератор—двигатель», при использовании которой частота вращения п2 двигателя ДПТ может поддерживаться постоянной при изменении частоты вращения я, двигателя ИД в широких пределах. Двигатель ДПТ приводит во вращение синхронный генератор СГ, который отдает часть потребляемой при испытаниях энергии в сеть. Регулирование нагрузки двигателя ИД. осуществляется увеличением тока возбуждения генератора ГПТ. что приводит к увеличению момента двигателя ДП Г и мощности синхронного генератора С Г. отдаваемой в сеть. 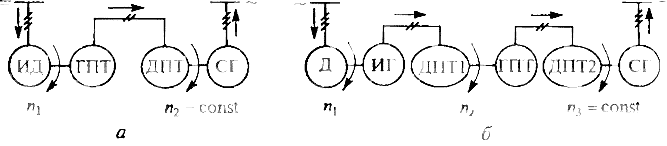
Рис. 1. Принципиальная схема испытания под нагрузкой электрических машин постоянного тока:
а — двигателя: б — генератора
При испытаниях под нагрузкой испытуемый генератор постоянного тока ИГ (рис. 1, б) приводится во вращение с частотой /f, двигателем Д (асинхронным при я, = const или постоянного тока при необходимости изменения п в соответствии с паспортными данными генератора ИГ). В качестве нагрузки генератора ИГ используется двигатель постоянного тока ДПТ1, энергия которого после тройного преобразования в машинах постоянного тока (генераторе ГПТ и двигателе ДПТ2) и синхронном генераторе СГ отдается в сеть переменного тока. Использование генератора ГПI и двигателя ДПТ2, соединенных по схеме «генератор—двигатель», вызвано необходимостью стабилизации частоты вращения пъ синхронного генератора СГ. На рис. 1 стрелками показано направление активной мощности, преобразуемой электрическими машинами.
В ряде случаев для упрощения схем испытания машин постоянного тока с возвратом энергии в сеть вместо механически связанных двигателя постоянного тока и синхронного генератора используют статический преобразователь постоянного тока в переменный требуемой частоты (инвертор), вход которого подключен к генератору ГПТ, а выход — к сети. Регулирование мощности в этом случае осуществляется за счет изменения длительности проводящего состояния преобразователя.
I Синхронные машины. Испытуемый синхронный двигатель ИД (рис. 2, а) питается от сети переменного тока (в случае необходимости регулирования напряжения двигатель соединяется с сетью через автотрансформатор или индукционный регулятор) и приводит во вращение нагрузочный генератор постоянного тока |ГПТ, якорь которого соединен с якорем двигателя постоянного тока ДПТ (схема «генератор—двигатель»), скорость которого поддерживается постоянной. 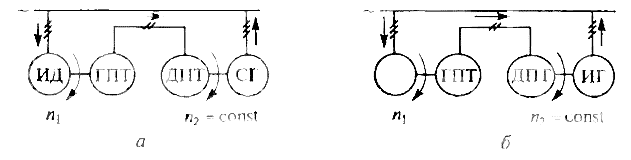
Принципиальная схема испытания под нагрузкой синхронных машин:
а — двигателя; б — генератора
Двигатель ДПТ механически соединен с синхронным генератором, отдающим энергию в сеть. Отметим, что нагрузочный генератор ГПТ на время запуска синхронного двигателя ИД, может использоваться в качестве разгонного двигателя, получая питание от сети постоянного тока. В этом случае может быть обеспечена точная синхронизация испытуемого синхронного двигателя с сетью без бросков тока.
При испытаниях под нагрузкой испытуемый синхронный генератор ИГ (рис. 2, б) приводится во вращение с неизменной частотой п2 = const двигателем постоянного тока ДПТ и работает параллельно с сетью. Двигатель ДПТ, как правило, подключается к генератору постоянного тока ГПТ, вращаемого асинхронным двигателем. Нагрузка генератора ИГ регулируется путем изменения момента на валу двигателя ДПТ.
Для согласования напряжения синхронного генератора и сети в схему стенда может быть при необходимости введен автотрансформатор или трансформатор соответствующей мощности. При наличии на испытательной станции отдельной регулируемой сети постоянного тока питание двигателя ДПТ может осуществляться непосредственно от этой сети, что позволяет существенно сократить комплект электрооборудования для испытаний.
При использовании схемы, приведенной на рис. 2, возбуждение машин постоянного тока ГПТ и ДПТ, образующих систему «генератор—двигатель», осуществляется от независимого источника постоянного тока, т.е. машины ГПТ и ДПТ имеют независимое возбуждение.
Асинхронные машины. Испытания асинхронного двигателя ИД под нагрузкой (испытания асинхронного генератора не рассматриваются, так как их применение ограничено) проводятся аналогично испытаниям синхронного двигателя по схеме, приведенной на рис. 2, а. Для согласования напряжения сети с напряжением испытуемого двигателя и синхронного генератора могут применяться трансформаторы или автотрансформаторы. В случае нестандартного напряжения двигателя могут использоваться также индукционные регуляторы.
В практике испытаний довольно широкое распространение получили нагрузочные стенды, использующие балансирную машину постоянного тока. Такие стенды получили название динамометрических тормозов постоянного тока и предназначены для измерения статических моментов как в двигательном, так и генераторном режимах работы испытуемой машины. 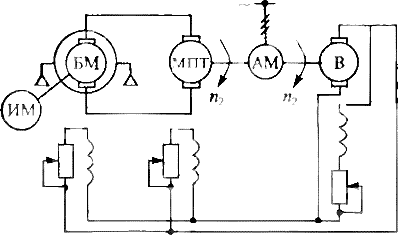
Рис. 3, Принципиальная схема нагрузочного стенда с использованием балансирной машины (БМ) постоянного тока
При работе балансирной машины постоянного тока БМ (рис. 3) в режиме генератора (испытуемая машина ИМ—двигатель) в качестве ее нагрузки используется машина постоянного тока МПТ, которая приводит во вращение асинхронную машину AM, работающую в режиме генератора, и возбудитель постоянного тока В. Регулирование мощности или момента на валу испытуемого двигателя осуществляется изменением частоты вращения асинхронного генератора с помощью машины постоянного тока. При работе в режиме двигателя (испытуемая машина—генератор) балансирная машина БМ получает питание от машины постоянного тока МПТ, приводимой во вращение вместе с возбудителем В асинхронной машиной AM, работающей в режиме двигателя.
Характеристики асинхронного двигателя



Существуют два метода получения данных для построения рабочих характеристик асинхронных двигателей:
1) Метод непосредственной нагрузки – заключается в опытном исследовании двигателя в диапазоне нагрузок от х. х. до режима номинальной нагрузки с измерением необходимых параметров. Этот метод применяют для двигателей мощностью не более (10÷15) кВт.
2) Косвенный метод – заключается в выполнении опыта х. х. и опыта к. з. Его применение не ограничивается мощностью двигателя. Опыты х. х. и к. з. асинхронных двигателей аналогичны таким же опытам трансформаторов, но имеют и некоторые особенности, обусловленные наличием у двигателей вращающегося ротора.
а) Опыт х. х. осуществляется при питании двигателя от регулятора напряжения, изменяя его в широких пределах; при этом вал двигателя свободен от механической нагрузки (рис.49). Опыт начинают с повышенного напряжения питания U1 = 1,15 U1 ном, затем постепенно понижая его до 0,4 U1 ном, снимают показания вольтметра (U0), амперметра (I0), ваттметра (P0) в 5÷7 точках. Затем вычисляют сумму магнитных и механических потерь P´0:
P´0 = P0-(m1×I0×r1),
где m1 – число фаз обмотки статора, r1 – активное сопротивление одной фазы обмотки статора.
Коэффициент мощности для режима х. х. cos φ0:
cos φ0 = P0/(m1×U1×I0).
По результатам измерений и вычислений строят характеристики х. х.: I0 = f(U1), P0 = f(U1), P´0 = f(U1), cos φ0 = f(U1) (рис. 50).
Рис. 49. Схема включения трёхфазного асинхронного двигателя при опытах холостого хода и короткого замыкания.
Рис. 50. Характеристики холостого хода трёхфазного асинхронного двигателя (3,0 кВт, 220/380 В, 1430 об/мин).
Коэффициент мощности для режима к.з. cos φк:
cos φк = Pк/(m1×Uк×Iк).
По результатам измерений и вычислений строят характеристики к. з.: Iк = f(Uк), Pк = f(Uк), cos φк = f(Uк) (рис. 51).
Рис. 51. Характеристики короткого замыкания трёхфазного асинхронного двигателя (3,0 кВт, 220/380 В, 1430 об/мин).
Зависимость n2 = f(P2) является скоростной характеристикой, показывающей, что с увеличением мощности на валу двигателя P2 частота вращения n2 уменьшается.
Зависимость M2 = f(P2) показывает, что при n2 = const её график представляет прямую линию, но с увеличением нагрузки n2 уменьшается и график M2 = f(P2) имеет криволинейный вид.
Зависимость cos φ1 = f(P2) показывает, что при увеличении нагрузки cos φ1 возрастает, достигая максимума (0,8÷0,9) при нагрузке близкой к номинальной.
Вид графика η = f(P2) имеет характер, общий для всех электрических машин.
Рис. 52. Рабочие характеристики асинхронного двигателя.
3.4.5. Пуск и регулирование частоты вращения трёхфазных асинхронных двигателей
Пусковые свойства двигателя определяются в первую очередь значением пускового тока Iп или его кратностью Iп/I1 ном. Двигатель, обладающий хорошими пусковыми свойствами, развивает значительный пусковой момент при сравнительно небольшом пусковом токе. Однако добиться этого в асинхронных двигателях сложно, а иногда и невозможно.
Пуск двигателей с фазным ротором (с контактными кольцами) можно осуществлять включением в цепь ротора пускового реостата (ПР) (рис. 53 ). При пуске сопротивление ПР уменьшают таким образом, чтобы ток ротора оставался приблизительно неизменным (I1 ном). ПР состоят из кожуха, рычага с переключающим устройством и сопротивлений из металлической проволоки или ленты. В асинхронных двигателях с фазным ротором обеспечивается наиболее благоприятное соотношение между пусковым моментом и пусковым током: большой пусковой момент при небольшом пусковом токе. Недостатком пусковых свойств двигателей с фазным ротором являются сложность, продолжительность и неэкономичность пусковой операции.
Рис. 53. Схема включения пускового реостата (ПР) при пуске асинхронного двигателя с фазным ротором.
Пуск двигателей с короткозамкнутым ротором осуществляются двумя способами (рис. ):
1) Непосредственное включение в сеть – при этом пусковой ток Iп = (5÷7) I1 ном, но он быстро спадает и поэтому, а также благодаря простоте, этот способ получил наибольшее распространение для двигателей мощностью до 50 кВт.
2) Понижение питающего напряжения – при этом понижается пусковой ток пропорционально понижению напряжения. Существует несколько способов понижения питающего напряжения:
Рис. 54. Схемы реакторного (а) и автотрансформаторного (б) способов пуска асинхронных двигателей с короткозамкнутым ротором.
в) автотрансформаторный пуск – осуществляется через понижающие автотрансформаторы (рис. 54,б.). При этом пусковой ток двигателя уменьшается в КА раз, где КА – коэффициент трансформации автотрансформатора. Автотрансформаторный пуск проходит тремя ступенями: на первой к двигателю подводится пониженное напряжение от вторичной обмотки автотрансформатора, на второй вторичные обмотки автотрансформаторов отключают и первичные работают как реакторы, на третьей к двигателю подводится номинальное напряжение. Недостатки: уменьшение пускового момента и сложность пусковой аппаратуры.
n2 = n1×(1-s) = (f×60/p)×(1-s).
1) Регулирование частоты вращения асинхронного двигателя изменением скольжения происходит только в нагруженном двигателе и возможно тремя способами: изменением подводимого к обмотке статора напряжения (осуществляется либо регулировочным трансформатором, либо реакторами, включенными в разрыв линейных проводов), нарушением симметрии этого напряжения (осуществляется включением в цепь одной из фаз однофазного регулировочного автотрансформатора) и изменением активного сопротивления обмотки ротора (осуществляется включением в цепь обмотки ротора регулировочного реостата РР – возможно только в двигателе с фазным ротором).
2) Регулирование частоты вращения асинхронного двигателя изменением частоты тока в обмотке статора (частотное регулирование) основано на зависимости синхронной частоты вращения n1 от частоты тока f1. Для осуществления этого способа регулирования необходим источник питания двигателя переменным током с регулируемой частотой.
3) Регулирование частоты вращения асинхронного двигателя изменением числа полюсов даёт ступенчатую регулировку. Так при f =50 Гц и p = (1÷5) можно получить следующие частоты вращения: 3000, 1500, 1000, 750, 600 об/мин. Изменяют число полюсов в обмотке либо укладкой на статоре двух обмоток с разным числом полюсов, либо укладкой одной обмотки, конструкция которой позволяет путём переключения катушечных групп получать различное число полюсов. Этот способ получил наибольшее распространение.
Аналитический метод расчета рабочих характеристик асинхронных двигателей
Рассмотренный графический метод расчета рабочих характеристик асинхронных двигателей с применением круговой диаграммы имеет существенный недостаток — необходимость построения этой диаграммы и неизбежную неточность как при построении, так и при ее последующем использовании, связанные с дополнительными построениями, измерениями отрезков и т. п. Аналитический метод расчета рабочих характеристик не предусматривает каких-либо графических изображений и измерений, а некоторое увеличение объема математических вычислений при условии применения простейшей вычислительной техники не вызывает каких-либо затруднений. Аналитический метод расчета основан на схеме замещения асинхронного двигателя (рис. 12.2, б). Исходными при этом являются паспортные данные двигателя (Рном, U1HOM, n2ном) и результаты выполнения опытов холостого хода и короткого замыкания (см. § 14.2 и 14.3).
Расчет ведут в следующем порядке.
Определяют приведенное активное сопротивление ротора (Ом):
а затем критическое скольжение:
и номинальное скольжение:
Задавшись рядом значений скольжения (всего 6—7 значений, в том числе номинальное shom и критическое sкр), определяют необходимые для построения рабочих характеристик величины.
Эквивалентное активное сопротивление (Ом)
Эквивалентное полное сопротивление рабочего контура схемы замещения (Ом)
Zэк = 
Коэффициент мощности рабочего контура схемы замещения
Приведенный ток ротора, (А)
и его активная и реактивная составляющие (А)
Активная и реактивная составляющие тока статора (А)
Здесь I0а = I0 соs φ0 — активная составляющая тока холостого хода; I0p = I0 sin φ0 — реактивная составляющая этого тока.
Ток в обмотке статора (А)
I1 = 
Коэффициент мощности двигателя
Потребляемая двигателем мощность (Вт)
Электрические потери статора Рэ1 определяют по (13.2), электромагнитную мощность Рэм — по (13.6), электромагнитный момент М — по (13.11), электрические потери в роторе Рэ2 — по (13.5), добавочные потери Рдоб — по (13.7) и (13.8).
Полезная мощность двигателя (Вт)
где Рмех — механические потери, Вт; их определяют из опыта холостого хода (см. рис. 14.2).
Коэффициент полезного действия двигателя определяют по (13.10), частоту вращения ротора — по (10.2). Полезный момент (момент на валу) двигателя (Н 
Результаты расчета сводят в таблицу (см. табл. 14.1), а затем строят рабочие характеристики двигателя (см. рис. 13.7).
Пример 14.1.Трехфазный асинхронный двигатель имеет паспортные данные: Рном =3,0 кВт, Uном = 220/380 В, I1ном = 6,3 А, nном = 1430 об/мин. Активное сопротивление фазы обмотки статора при рабочей температуре r1 = 1,70 Ом. Характеристики х.х. двигателя приведены на рис. 14.2 (I0ном = 1,83 А, Рном = 300 Вт, Р / 0ном = 283 Вт, Рмех = 200 Вт, соs φ0ном = 0,24, обмотка статора соединена звездой). Характеристики к.з. приведены на рис. 14.3 (Рк.ном = 418 Вт, Uк.ном = 59,5 В, Iк.ном = 6,3 А, cos φк.ном =0,372).
Требуется рассчитать данные и построить рабочие характеристики двигателя и определить перегрузочную его способность.
Решение. Активная и реактивная составляющие тока х.х.
Полное сопротивление кз. по (14.10)
его активная и реактивная составляющие по (14.11) и (14.12)
xк = 

Приведенное активное сопротивление ротора по (14.30)
Критическое скольжение по (14.31)
Номинальное скольжение по (14.32)
Магнитные потери по (14.8)
Задаемся следующими значениями скольжения: 0,01, 0,02, 0,03, 0,046, 0,06 и 0,20. Результаты расчета приведены в табл. 14.1. Рабочие характеристики двигателя представлены на рис. 13.7.
Перегрузочная способность двигателя λ = Мmax/ Mном = 38,7/ 21,4 = 1,81.
Таблица 14.1
| Значения параметров при скольжении s | 0,01 | 0,02 | 0,03 | 0,046 | 0,06 | 0,20 |
| r / 2/s, Ом | 39,1 | 10,1 | ||||
| rэк = r1 + r / 2/ s, Ом | 181,7 | 91,7 | 61,7 | 40,8 | 31,7 | 11,8 |
zэк =  , Ом , Ом | 62,5 | 33,2 | 15,5 | |||
| cos φ2 = rэк/ zэк | 0,998 | 0,996 | 0,987 | 0,971 | 0,955 | 0,760 |
| I / 2 = U1/ zэк, А | 1,21 | 2,39 | 3,52 | 5,24 | 6,63 | 14,20 |
| I / 2a = I / 2 cos φ2, А | 1,21 | 2,38 | 3,47 | 5,09 | 6,33 | 10,7 |
| I / 2p = I / 2 sin φ2, А | 0,08 | 0,19 | 0,57 | 1,25 | 1,95 | 9,20 |
| I1a = I0a + I / 2a, А | 1,65 | 2,82 | 3,91 | 5,54 | 6,77 | 11,10 |
| I1p = I0p + I / 2p, А | 1,85 | 1,96 | 2,34 | 3,02 | 3,72 | 10,9 |
I1 =  , A , A | 2,48 | 3,43 | 4,55 | 6,30 | 7,70 | 15,5 |
| cos φ1 = I1a/ I1 | 0,66 | 0,82 | 0,86 | 0,88 | 0,88 | 0,71 |
| P1 = m1U1I1a, Вт | ||||||
| Рэ1 = m1I1 2 r1, Вт | 31,0 | 60,0 | ||||
| Рэм = Р1 – Рэ1 – Рм,Вт | ||||||
М = Рэм/ ω1, Н  м м | 6,2 | 10,9 | 15,3 | 21,4 | 26,0 | 38,7 |
| Рэ2 = s Рэм, Вт | — | |||||
| β 2 =(I1/ I1ном) 2 | 0,15 | 0,29 | 0,52 | 1,0 | 1,44 | — |
| Р / доб = β 2 Рдоб.ном, Вт | 2,7 | 5,2 | 9,4 | — | ||
| Р2 = Рэм – Рэ2 – —Рмех – Рдоб, Вт | — | |||||
| η = Р2/ Р1 | 0,70 | 0,79 | 0,82 | 0,82 | 0,81 | — |
| n2 = n1(1-s), об/мин | — | |||||
М2 = 9,55Р2/ n2, Н  м м | 4,9 | 9,6 | 13,8 | 20,0 | 24,5 | — |
Контрольные вопросы
1.Какие существуют методы получения данных для построения рабочих характеристик асинхронных двигателей?
2.Чем ограничивается применение метода непосредственной нагрузки?
3.Как определить величину механических и магнитных потерь двигателя по характеристикам х.х.?
ГЛАВА 15
• Пуск и регулирование частоты вращения трехфазных асинхронных двигателей