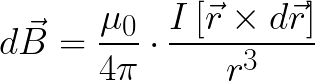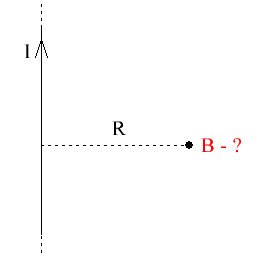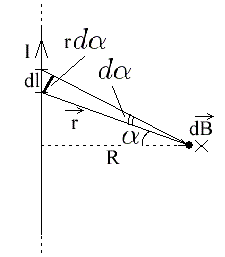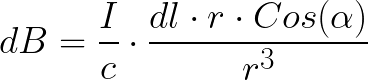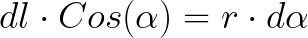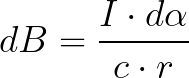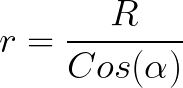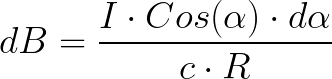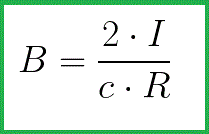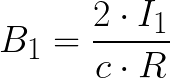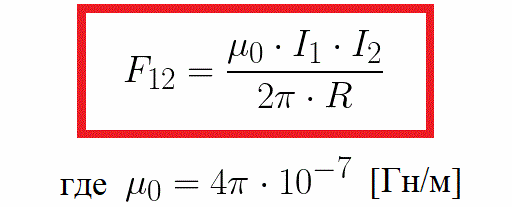Чем объясняется взаимодействие двух параллельных проводников с током
Взаимодействие параллельных проводников с током (параллельных токов)
Определить в некоторой точке пространства вектор индукции магнитного поля B, порождаемого постоянным электрическим током I, можно с помощью Закона Био-Савара. Это делается путем суммирования всех вкладов в магнитное поле от отдельных элементов тока.
Магнитное поле элемента тока dI, в точке, заданной вектором r, по Закону Био-Савара находится так (в системе СИ):
Одна из типичных задач состоит в том, чтобы далее определить силу взаимодействия двух параллельных токов. Ведь токи, как известно, порождают собственные магнитные поля, а ток, находящийся в магнитном поле (другого тока) испытывает на себе действие силы Ампера.
Прежде всего для прямого тока I нам необходимо найти магнитное поле B на некотором расстоянии R от него.
Сначала будем записывать выражения в системе СГС, то есть появится коэффициент 1/с, а в конце приведем запись в системе СИ, где появится магнитная постоянная.
Произведение косинуса на dl можно выразить через r и угол:
Значит выражение для dB примет вид:
Далее выразим r через R и косинус угла:
И выражение для dB примет вид:
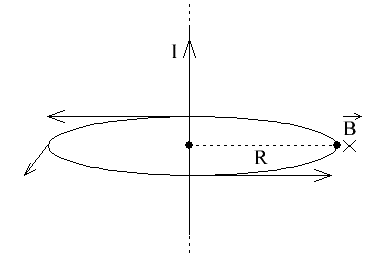
Можно сказать, что вектор B найденной величины, для выбранной окружности радиуса R, через центр которой перпендикулярно проходит данный ток I, всегда будет направлен по касательной к данной окружности, какую бы точку окружности мы ни выбрали. Здесь присутствует осевая симметрия, так что вектор B в любой точке окружности получается одной и той же длины.
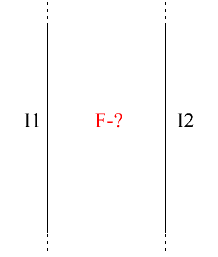
Теперь рассмотрим параллельные постоянные токи и решим задачу нахождения сил их взаимодействия. Допустим, что параллельные токи направлены в одну и ту же сторону.
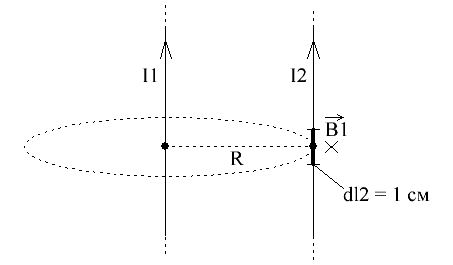
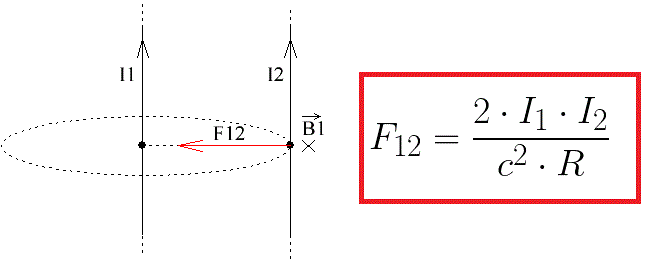
Изобразим магнитную силовую линию в форме окружности радиуса R (о которой речь шла выше). И пусть второй проводник расположен параллельно первому в какой-то точке данной силовой линии, то есть в месте с индукцией, значение которой (в зависимости от R) мы только что научились находить.
Магнитное поле в этом месте направлено за плоскость рисунка, и оно действует на ток I2. Выделим элемент длины тока l2, равный одному сантиметру (единица длины в системе СГС). Далее рассмотрим силы, действующие на него. Будем использовать Закон Ампера. Индукцию в месте расположения элемента длины dl2 тока I2 мы нашли выше, она равна:
Следовательно сила, действующая со стороны всего тока I1 на единицу длины тока I2 будет равна:
Это и есть сила взаимодействия двух параллельных токов. Поскольку токи однонаправленные и они притягиваются, то сила F12 со стороны тока I1 направлена так, что она тянет ток I2 в сторону тока I1. Со стороны же тока I2 на единицу длины тока I1 действует сила F21 равной величины, но направленная в сторону противоположную силе F12, в соответствии с третьим законом Ньютона.
В системе СИ, сила взаимодействия двух постоянных параллельных токов находится по следующей формуле, где коэффициент пропорциональности включает в себя магнитную постоянную:
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети: