Чем объяснить что с повышением температуры уменьшается поверхностное натяжение и вязкость

Поверхностное натяжение и температура

На рисунке 1, взятом из справочника «Физические величины» (под редакцией И. С. Григорьева и Е. З. Мейлихова), видно, что зависимости коэффициентов поверхностного натяжения σ для разных сжиженных газов выглядят похожим образом — они весьма близки к линейным. Диапазон температур, в котором существует жидкое состояние вещества, для каждого вещества определяется двумя точками: температурой плавления (а точнее, температурой тройной точки) и критической температурой. Пользуясь моделью взаимодействия молекул, размеры которых D, можно дать объяснение этим зависимостям. Суть в том, что у молекул, находящихся на поверхности раздела конденсированной и газообразной фаз вещества, усредненное число Z_пов ближайших соседок, каждая из которых обеспечивает молекуле на поверхности вклад в глубину потенциальной ямы U₀, меньше соответствующего числа Z_внутр соседок у молекул, находящихся внутри конденсированной фазы. С ростом температуры плотность газообразной фазы растет, а плотность конденсированной фазы убывает, и это соответствует уменьшению разницы (Z_внутр − Z_пов). В результате микроскопическая поверхностная энергия, приходящаяся на площадку с размерами порядка размеров одной молекулы (S ≈ D 2 ) и равная

убывает с ростом температуры.

При низких температурах поверхность жидкости почти плоская, это похоже на поверхность моря в отсутствие ветра (рис. 2, слева). А если температура высокая, то поверхность получается «развитая» — как поверхность моря, покрытая волнами (рис. 2, справа). Чем выше температура, тем больше получается реальная площадь поверхности раздела «жидкость–пар» при том же самом «теоретическом» периметре этой поверхности. Этот образ — поверхность моря с волнами — позволяет понять, почему для увеличения поверхности на ΔS нужна дополнительно к работе внешних сил теплота и почему с ростом температуры уменьшается коэффициент поверхностного натяжения.

Законно поставить вопрос: а каков вклад во внутреннюю энергию жидкости участка ее поверхности, который имеет площадь S₀ (плоская поверхность, ограниченная периметром), и как этот вклад зависит от температуры?

Если рассматривать поверхностный слой молекул как промежуточную фазу вещества (между конденсированным и газообразным состоянием), то для перевода молекул из конденсированной фазы в эту промежуточную фазу нужно сообщить им дополнительную тепловую энергию и при этом внешние силы должны совершить механическую работу. В результате внутренняя энергия увеличивается. Ситуация здесь аналогична переходу вещества из конденсированного состояния в газообразное. Отличаются только знаки работ внешних сил. При испарении вещества внешние силы (силы давления снаружи) совершают отрицательную работу, а при увеличении площади поверхности жидкости внешние силы совершают положительную работу. Собственно, именно поэтому давление насыщенных паров растет с ростом температуры, а коэффициент поверхностного натяжения уменьшается.

Если считать, что на проведенной (мысленно) границе, выделяющей участок поверхности жидкости S₀, поверхность жидкости колеблется, то среднее значение косинуса угла α между реальной поверхностью жидкости и плоской поверхностью S₀, натянутой (мысленно) на границу, вместе с микроскопической величиной поверхностной энергии σ, приходящейся на единицу площади, определяют проекцию силы натяжения прямого участка границы длиной ΔL₀ на плоскую поверхность: σΔL₀cos α. С другой стороны, если мысленно провести к «средней» по времени плоскости поверхности жидкости перпендикулярно ей плоскость и зафиксировать длину отрезка пересечения (части периметра), то при выделенном мысленно «прямом» отрезке периметра «реальная» длина границы раздела за счет волнистости поверхности будет больше. Если угол между «прямым» участком границы и реальным равен β, то реальная длина участка поверхности стала больше: ΔL₀ / cos β. И вместе эти два фактора в среднем по времени должны компенсировать друг друга. Так как средние значения углов наклона α и β, очевидно, одинаковые, то усредненное значение проекции силы на плоскую поверхность будет равно

где σ — величина коэффициента поверхностного натяжения, приводимая в справочнике.

Внешние силы при увеличении площади поверхности жидкости на S₀ совершают работу

При этом дополнительная тепловая энергия Q, нужная для того, чтобы при увеличении площади «плоской» поверхности на S₀ сохранилась температура жидкости, на самом деле идет на то, чтобы создалась дополнительная большая площадь поверхности. Измеренная суммированием по всем микроскопическим изгибам поверхности площадь может быть в несколько раз больше площади поверхности: S₀ → S = S₀k, где k > 1. В итоге закон сохранения энергии Q + A = ΔU дает такое соотношение:

Коэффициент поверхностного натяжения (данные справочника) изменяется с температурой линейно. Эту зависимость можно описать формулой

Здесь \( σ_ \) — коэффициент поверхностного натяжения при некоторой температуре T₀, а T — текущая температура. Если устроить тепловой двигатель, работающий по циклу Карно с нагревателем и холодильником, имеющими близкие температуры T + ΔT и T, в котором в качестве рабочего тела будет выступать пленка поверхности жидкости, то КПД такого двигателя будет равен Δt/T и можно написать такое соотношение:

Сократив на одинаковые множители, получаем

Подставим полученное выражение в формулу для Q:

Если добавить к этой энергии работу внешних сил, то получится вклад во внутреннюю энергию жидкости при температуре T ее поверхности величиной S₀ (плоская поверхность с заданным периметром):

Ответ на поставленный вопрос получен.

Как видно из формулы для ΔU, в знаменателе стоит разность температур, которая при приближении T к T_крит стремится к нулю. Но и сам коэффициент σ_T тоже стремится к нулю. Подставим в формулу значение σ_T, выраженное через значение при некоторой температуре T₀:

Получилась удивительная вещь: добавок внутренней энергии, связанный с наличием свободной поверхности, не зависит от температуры!

Имеется отдаленная аналогия с известной задачей о запасе энергии теплового движения воздуха в комнате при разных температурах воздуха, но при фиксированном давлении. И там тоже запас энергии не зависит от температуры, а определяется только давлением воздуха и объемом комнаты.

Источник

Природа поверхностной энергии. Поверхностное натяжение

» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>

Природа поверхностной энергии. Поверхностное натяжение. ТЕРМОДИНАМИКА МЕЖФАЗНОЙ ПОВЕРХНОСТНОСТИ

Наиболее важной характеристикой поверхности является поверхностное натяжение а.

Поверхностное натяжение – это избыточная энергия, приходя­щаяся на единицу площади поверхности:

Физическая природа поверхностного натяжения в нескомпенсированности поля межмолекулярных сил на межфазных поверхностях.

Поверхностное натяжение характеризует различия в интенсивности межмолекулярных взаимодействий граничащих фаз. Чем сильнее межмолекулярные связи в веществе, тем больше поверхностное натяжение на его межфазной поверхности.

С термодинамической точки зрения, поверхностное натяжение определяется частной производной от любого термодинамического потенциала по величине площади межфазной поверхности при постоянстве других параметров. Используя потенциал Гиббса (G), можно записать

где р – давление; Т- температура; п. – число молей компонентов.

Поверхностная энергия является частью свободной энергии системы в целом. В самопроизвольных процессах эта энергия мо­жет быть снижена либо за счет уменьшения площади поверхнос­ти и изменения ее формы, либо за счет снижения поверхностного натяжения.

Факторы, влияющие на поверхностное натяжение

Поверхностное натяжение на границе раздела фаз между жид­костью и газом определяют следующие факторы: химическая при­рода вещества, температура, природа граничащих фаз, наличие примесей, заряд поверхности, кривизна поверхности жидкости.

Энергия межмолекулярных взаимодействий зависит от температуры, а значит, имеет выраженную температурную зависимость.

Взаимосвязь поверхностного натяжения, температуры и пол­ной поверхностной энергии (внутренней энергии поверхностного слоя) U_s выражается уравнением Гиббса – Гельмгольца:

Рис. 2.1. Зависимость поверхностного натяжения жидкостей от температуры: вода (У), глицерин (2), нитробензол (3), гексан (4).

С повышением температуры поверхностное натяжение уменьшается, а теплота образования единицы площади поверхности увеличивается. Это объясняется тем, что с повышением температуры расстояние между молекулами в жидких телах увеличивается, и соответственно равнодействующая межмолекулярных сил (и, следовательно, поверхностное натяжение) уменьшается. С помощью температурного коэффициента можно определить поверхностное натяжение при любой температуре, если известно значение поверхностного натяжения при какой-то температуре, т. е.

Появление кривизны поверхности из-за стремления системы

к минимуму поверхностной энергии ведет не только к изменению площади межфазной поверхности, но и к появлению избыточного давления внутри фаз. Взаимосвязь между избыточным внутренним давлением в теле и кривизной его поверхности выражается урав­нением Лапласа:

Искривление поверхности вызывает повышение или пониже­ние давления в фазе по сравнению с плоской поверхностью фазы такого же химического состава. Очевидно, что это приводит к из­менению термодинамических параметров вещества, которые опре­деляют его физические свойства и реакционную способность. По­нятие термодинамическая реакционная способность вещества характеризует его способность изменять химический или фазо­

вый состав, т. е. вступать в химическую реакцию или переходить в новую фазу (например, испаряться или конденсироваться, раст­воряться).

У тел с искривленной поверхностью меняется не только внут­реннее давление, но и его свободная энергия

Уравнение показывает, что приращение реакционной способ­ности пропорционально 1/r- кривизне поверхности или дисперс­ности. Чем выше кривизна поверхности или дисперсность, тем выше ее влияние на реакционную способность.

При переходе из газообразного состояния в жидкое

гдер – давление пара над искривленной поверхностью; p_s– давление пара над плоской поверхностью.

Тогда уравнение, записанное для сферической поверхности, на­зывается уравнением капиллярной конденсации Кельвина (Томсона):

Из анализа данного уравнения можно сделать вывод о том, что при положительной кривизне жидкости (капля в невесомости или на поверхности твердого тела при отсутствии или неполной сма­чиваемости) над ней создается повышенное по сравнению с плос­кой поверхностью давление пара, т. е. испаряется больше жидкос­ти. При отрицательной кривизне (жидкость, смачивающая капил­ляр) количество испарившейся жидкости в равновесии с ее паром будет меньше по сравнению с плоской поверхностью; иными слова­ми, конденсация будет происходить при меньшем давлении паров.

При появлении кривизны поверхности и увеличении степени дисперсности уменьшается и температура фазовых переходов.

Свободная энергия единицы поверхности и поверхностное натяжение

3.1. Поверхностные свойства веществ

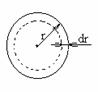
Если взять частицу внутри жидкости и, рассматривая ее как точку, провести сферу радиуса действия межчастичных сил, то за промежуток времени, больший по сравнению с периодом собственных колебаний, на частицу будут действовать силы, одинаковые во всех направлениях.

Следовательно, силовое поле атомов или молекул в объеме жидкости симметрично. Частицы в глубине и на поверхности имеют разные силовые поля. На поверхности жидкости частица будет испытывать преимущественное притяжение со стороны жидкой фазы. Если вторая фаза — пар или газ, то силами взаимодействия со стороны другой фазы можно пренебречь. Если вторая фаза — жидкость, то равнодействующая будет другая.

В общем случае межчастичные силы на межфазной границе несимметричны. Наличие такой асимметрии силового поля приводит к тому, что появляется равнодействующая, направленная перпендикулярно поверхности. Под действием этой силы поля частица втягивается вглубь жидкости. Если частицы уподобить шарикам, то перемещение подвижных частиц жидкости можно проиллюстрировать следующим рис. 3.3:

Когда частица из поверхностного слоя уйдет в объем жидкости, между оставшимися двумя соседними частицами будут действовать силы притяжения. Силы притяжения между частицами В и С сближают поверхностные частицы, поэтому жидкость самопроизвольно сокращает свою поверхность. Такой характер поведения жидкости обусловлен ее текучестью. Если на жидкость не действуют никакие другие силы, то жидкость принимает форму сферы, обладающей минимальной поверхностью. Если же действуют силы тяжести, то форма жидкости может быть другой. При малом объеме жидкости поверхностные силы намного превосходят силы тяжести и жидкость собирается в сферическую капельку. По мере увеличения объема жидкости эти силы становятся соизмеримыми и получается приплюснутая капля. В случае большого объема жидкости силы тяжести значительно больше поверхностных сил и жидкость принимает форму сосуда.

Если увеличивать поверхность жидкости, то на это увеличение нужно затрачивать работу: δА — работа увеличения поверхности на dω. При обратимом изотермическом процессе эта работа максимальна и равна убыли свободной энергии системы: δАмакс = –dF. Изменение свободной энергии, отнесенной к единице поверхности при постоянных объеме и температуре (V, T = const), называется свободной энергией единицы поверхности, или поверхностным натяжением.

F Работа δА отрицательна, так как работу совершаем мы, а не система. Размерность поверхностного натяжения:

Энергия на единицу поверхности. Эти размерности можно преобразовать:

Сила, действующая на поверхности жидкости, направленная по касательной к этой поверхности. Эту силу называют поверхностным натяжением — это сила на единицу длины, действующая по касательной к поверхности. Количественно свободная энергия единицы поверхности жидкости равна поверхностному натяжению, однако отождествлять их нельзя. Энергия — это скалярная величина, а сила — векторная. Они совпадают только в изотропных средах. В анизотропных средах (кристаллах) эти характеристики могут существенно отличаться. В кристаллических телах сила — не вектор, а тензор. Вектор можно задать тремя числами, а тензор определяется числовой матрицей, т. е. набором чисел. Если этих чисел три, то имеем вектор r (x, y, z). Если состояние напряженное, то надо знать напряжение по различным направлениям.

Натяжение в общем случае нужно рассматривать как тензор. Поэтому в кристаллах нельзя отождествлять свободную энергию и поверхностное натяжение. В жидкости они совпадают количественно, и обычно в литературе их отождествляют:

Поверхностное натяжение жидкостей обычно определяют на границе с их собственным насыщенным паром или инертным газом. Величина свободной энергии зависит от свойств жидкости и является вполне определенной. Поверхностное натяжение жидкости — ее свойство, ее характеристика при данной температуре. Натяжение на границе двух конденсированных фаз (ж1‑ж2, ж‑тв) зависит от свойств каждой жидкости и является их совместной характеристикой. Поэтому его называют межфазным натяжением. Размерность та же.

Для конденсированных фаз при малых давлениях F ≈ G, и обычно технологи пользуются энергией Гиббса. F (V, T), G (P, T) — в скобках записаны независимые переменные.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 2.1.

Пример 2.2.

Пример 2.3.

Пример 2.4.

По экспериментальным данным (табл. 2.1) температурной зависимости поверхностного натяжения найти температурный коэффициент.

Источник

1.2. Зависимость поверхностного натяжения жидкостей от температуры

Как известно, с увеличением температуры интенсивность межмолекулярного взаимодействия уменьшается, поэтому снижается и поверхностное натяжение жидкостей на границе с воздухом или с собственным паром. Вдали от критической температурыповерхностное натяжение уменьшается прямо пропорционально росту температуры. Эту зависимость обычно описывают эмпирическим уравнением

 1 1.11

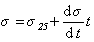
Температурный коэффициент поверхностного натяжения, имеющий отрицательное значение, остается постоянным вдали от критической температуры. При температуре, близкой к критической, поверхностное натяжение резко снижается вплоть до нуля. Следует отметить, что такая зависимость справедлива только для чистых жидкостей, тогда как для растворов наряду с изменением поверхностного натяжения возможно изменение концентрации растворенного вещества в поверхностном слое, что приведет к вторичным эффектам, способным вызвать повышение поверхностного натяжения. Полная внутренняя энергия при изменении температуры вдали от критической остается практически неизменной (изменяется лишь при температуре, близкой к температуре исчезновения поверхности раздела фаз).

Эмпирическое уравнение, устанавливающее зависимость поверхностного натяжения от температуры, предложил Этвеш. Интегральная форма этого уравнения имеет вид

, (1.1.14)

, (1.1.15)

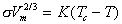
где n=11/9 для многих органических жидкостей, n=1 для металлов; s₀ – гипотетическое поверхностное натяжение при температуре 0 K; для постоянной K уравнения (1.1.14) получаем выражение

Уравнения (1.1.15) и (1.1.16) достаточно корректны для неполярных жидкостей, а для воды дают большую погрешность. Из уравнения (1.1.16) следует размерность постоянной K [Дж/град·моль 2/3 ], что не имеет физического смысла. Если относить эту постоянную к одной молекуле, то для большинства жидкостей получается величина, соответствующая постоянной Больцмана 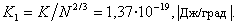Из этого следует, что уравнение Этвеша достаточно строго можно вывести из статистико-механической теории жидкостей.

Строгое уравнение зависимости поверхностного натяжения от температуры можно получить из уравнения Гиббса-Гельмгольца

, (1.1.17) где индекс s указывает на отнесение энтальпии энергии Гиббса и энтропии к единице площади поверхности. Часто энтальпия и полная внутренняя энергия поверхности неразличимы и могут хорошо аппроксимировать друг друга. Поэтому уравнение (1.1.17) можно записать , (1.1.18)

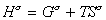
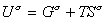
или, учитывая, что для единицы площади поверхности G s =s, запишем

, (1.1.19) где . Учитывая, что , (1.1.20)

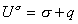
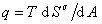
можем записать для единицыплощади поверхности

(1.1.21)

, (1.1.22)

. (1.1.23)

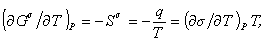
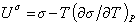
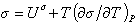
Уравнение (1.1.23) описывает зависимость поверхностного натяжения от температуры. Уравнение (1.1.22) может быть также записано в виде

, (1.1.24)

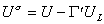
Уравнение (1.1.24) известно как уравнение Гугенгейма-Гудриха.

Зная температурный коэффициент поверхностного натяжения, можно рассчитать внутреннюю энергию поверхности. Для многих неполярных жидкостей энергия U s остается постоянной и в широкой области температуры вплоть до критической, вблизи которой как s, так и U s резко уменьшаются вплоть до нуля.

Действительно, независимость U s от температуры становится очевидной, если продифференцировать по температуре уравнение Гиббса-Гельмгольца для поверхностного слоя:

. (1.1.25)

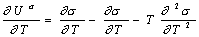
Поскольку для многих жидкостей первая производная поверхностного натяжения по температуре имеет постоянную величину в широкой области температуры и лишь вблизи критической температуры теряет это свойство, то

Рис. 1.3. Зависимость энергетических параметров поверхности от температуры

(1.1.27)

Рис. 1.4. Схема изменения объема пузырька газа в жидкости

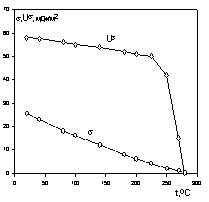
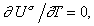
При критической температуре, когда свойства пара и жидкости становятся одинаковыми и исчезает поверхность раздела фаз, все энергетические поверхностные характеристики системы стремятся к нулю, как это показано на рис. 1.3.

Источник