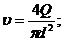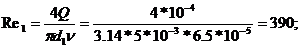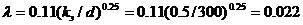Чем обусловлены потери на трение
Таким образом, ламинарное и турбулентное движение представляют два различных вида движения. Они отличаются не только характером движения частиц, но также особенностями распределения скоростей по сечению и видом зависимости между гидравлическим сопротивлением и скоростью.
5. ПОТЕРИ НАПОРА ПРИ ДВИЖЕНИИ ЖИДКОСТИ
При течении реальной жидкости возникают силы сопротивления, обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком превращается в тепловую энергию. Следовательно, при течении жидкости происходит процесс необратимого превращения части механической энергии во внутреннюю энергию. Работа сил вязкости, произведенная между двумя сечениями потока и отнесенная к единице веса движущейся жидкости, называется потерями напора 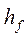
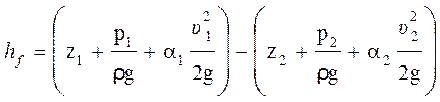
где 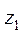
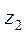
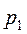
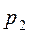
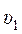
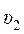
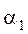
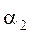
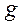
Потери напора при движении жидкости складываются из потерь напора на трение 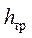
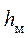
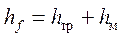
5.1. Потери напора на трение
Потери напора на трение, или потери по длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при равномерном течении жидкости. Для горизонтальной трубы постоянного сечения (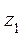
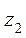
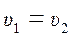
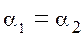
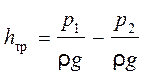
Таким образом, при равномерном движении жидкости потери напора по длине трубы определяются разностью пьезометрических высот в сечениях.
Общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов, имеет вид
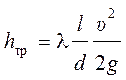
где 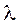
Эта зависимость называется формулой Дарси-Вейсбаха.
5.2. Понятие шероховатости поверхности
Для грубой количественной оценки шероховатости используется понятие средней высоты выступов. Эта высота, измеряемая в линейных единицах, называется абсолютной шероховатостью и обозначается обычно буквой Δ.
При одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений различно в зависимости от диаметра трубы. Поэтому вводится понятие относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы, т. е. Δ/d.
Кроме того, даже при одной и той же абсолютной шероховатости и одинаковом диаметре трубы из разного материала могут иметь совершенно различное сопротивление в зависимости от формы выступов, густоты и характера их расположения и т. д. Учесть это влияние непосредственными измерениями практически невозможно. В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной разнозернистой шероховатости Δэ. Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает одинаковую с заданной шероховатостью величину коэффициента гидравлического трения λ.
5.3. Коэффициент гидравлического трения
При ламинарном движении расчетная зависимость для 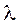
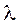
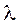
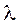
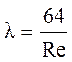
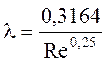
Чтобы распечатать файл, скачайте его (в формате Word).
СОДЕРЖАНИЕ
Экономика
Потери на трение представляют собой серьезную экономическую проблему везде, где текучие среды заставляют течь, независимо от того, полностью ли они заключены в трубу или канал, или с поверхностью, открытой для воздуха.
Определение
В следующем обсуждении мы определяем объемный расход V̇ (т. Е. Объем протекающей жидкости) как
V ˙ знак равно π р 2 v <\ displaystyle <\ dot
r = радиус трубы (для трубы круглого сечения внутренний радиус трубы). v = средняя скорость жидкости, протекающей по трубе. A = площадь поперечного сечения трубы.
Характеристики потерь на трение
Потери на трение, которые возникают из-за напряжения сдвига между поверхностью трубы и текучей средой, протекающей внутри, зависят от условий потока и физических свойств системы. Эти условия можно заключить в безразмерное число Re, известное как число Рейнольдса.
Потери на трение в прямой трубе
Факторы, отличные от потока в прямой трубе, вызывают потери на трение; они известны как «незначительные потери»:
В целях расчета общих потерь на трение в системе источники трения формы иногда сокращают до эквивалентной длины трубы.
Измерения
Из-за важности потерь на трение в гражданском строительстве и в промышленности они широко изучаются уже более века.
Шероховатость поверхности
Шероховатость поверхности трубы или канала влияет на поток текучей среды в режиме турбулентного потока. Обычно обозначаемые ε, значения, используемые для расчета расхода воды, для некоторых репрезентативных материалов:
| в | ||
|---|---|---|
| Гофрированные пластиковые трубы (видимая шероховатость) | 3.5 | 0,14 |
| Зрелые грязные канализации | 3.0 | 0,12 |
| Водопровод стальной с общими бугорками | 1.2 | 0,047 |
| Клепанная сталь | 0,9–9,0 | 0,035–0,35 |
| Бетон (асфальт с тяжелой щеткой или размытый острым материалом), Кирпич | 0,5 | 0,02 |
| Конкретный | 0,3–3,0 | 0,012–0,12 |
| Деревянный посох | 0,2–0,9 | 5–23 |
| Оцинкованные металлы (нормальная отделка), Чугун (с покрытием и без покрытия) | 0,15–0,26 | 0,006–0,010 |
| Асфальтированный чугун | 0,12 | 0,0048 |
| Бетон (новый или довольно новый, гладкий) | 0,1 | 0,004 |
| Стальные трубы, Оцинкованные металлы (гладкая поверхность), Бетон (новый, необычно гладкий, с гладкими стыками), Асбестоцемент, Гибкая прямая резиновая труба (с гладким отверстием) | 0,025–0,045 | 0,001–0,0018 |
| Коммерческая или сварная сталь, кованое железо | 0,045 | 0,0018 |
| ПВХ, латунь, медь, стекло, другие тянутые трубы | 0,0015–0,0025 | 0,00006–0,0001 |
При расчете потерь на трение в воздуховодах (например, для воздуха) используются следующие значения:
| в | ||
|---|---|---|
| Гибкий воздуховод (открытые провода) | 3,00 | 0,120 |
| Гибкий воздуховод (провода покрыты) | 0,90 | 0,036 |
| Оцинкованная сталь | 0,15 | 0,006 |
| ПВХ, нержавеющая сталь, алюминий, черный чугун | 0,05 | 0,0018 |
Расчет потерь на трение
Хаген – Пуазей
В ламинарном потоке (т.е. при Re Дарси – Вайсбах
Во многих практических инженерных приложениях поток жидкости более быстрый, поэтому турбулентный, а не ламинарный. При турбулентном потоке потери на трение примерно пропорциональны квадрату скорости потока и обратно пропорциональны диаметру трубы, то есть потери на трение подчиняются феноменологическому уравнению Дарси – Вайсбаха, в котором гидравлический уклон S может быть выражен
Обратите внимание, что значение этого безразмерного коэффициента зависит от диаметра трубы D и шероховатости поверхности трубы ε. Кроме того, оно также зависит от скорости потока V и физических свойств жидкости (обычно сводится к числу Рейнольдса Re). Таким образом, потери на трение не прямо пропорциональны квадрату скорости потока или обратной величине диаметра трубы: коэффициент трения учитывает оставшуюся зависимость от этих параметров.
Согласно экспериментальным измерениям, общие особенности изменения f D для фиксированной относительной шероховатости ε / D и числа Рейнольдса Re = V D / ν>
| NPS | D | S | Re | f D | Q | V | |||
|---|---|---|---|---|---|---|---|---|---|
| в | мм | в | галлонов в минуту | lps | фут / с | РС | |||
| ½ | 15 | 0,622 | 0,01 | 4467 | 5,08 | 0,9 | 0,055 | 0,928 | 0,283 |
| ¾ | 20 | 0,824 | 0,01 | 7301 | 5,45 | 2 | 0,120 | 1,144 | 0,349 |
| 1 | 25 | 1.049 | 0,01 | 11090 | 5,76 | 3.8 | 0,232 | 1,366 | 0,416 |
| 1½ | 40 | 1,610 | 0,01 | 23121 | 6,32 | 12 | 0,743 | 1,855 | 0,565 |
| 2 | 50 | 2,067 | 0,01 | 35360 | 6,64 | 24 | 1,458 | 2,210 | 0,674 |
| 3 | 75 | 3,068 | 0,01 | 68868 | 7,15 | 70 | 4,215 | 2,899 | 0,884 |
| 4 | 100 | 4,026 | 0,01 | 108615 | 7,50 | 144 | 8,723 | 3,485 | 1.062 |
| 6 | 150 | 6,065 | 0,01 | 215001 | 8,03 | 430 | 26,013 | 4,579 | 1,396 |
| 8 | 200 | 7,981 | 0,01 | 338862 | 8,39 | 892 | 53,951 | 5,484 | 1,672 |
| 10 | 250 | 10,020 | 0,01 | 493357 | 8,68 | 1631 | 98,617 | 6,360 | 1,938 |
| 12 | 300 | 11,938 | 0,01 | 658254 | 8,90 | 2592 | 156,765 | 7,122 | 2,171 |
Обратите внимание, что в цитируемых источниках рекомендуется поддерживать скорость потока ниже 5 футов в секунду (
Также обратите внимание, что данное f D в этой таблице на самом деле является величиной, принятой NFPA и отраслью, известной как C, которая имеет британские единицы фунт / кв.дюйм / (100 галлонов в минуту 2 фута) и может быть рассчитана с использованием следующего соотношения:
Расчет потерь на трение для воздуха в воздуховоде
В следующей таблице указан расход Q такой, что потери на трение на единицу длины Δ p / L (кг / м 2 / с 2 в системе СИ) составляют 0,082, 0,245 и 0,816, соответственно, для различных номинальных размеров воздуховода. Три значения, выбранные для потерь на трение, соответствуют в единицах США дюйм водяного столба на 100 футов, 0,01, 0,03 и 0,1. Обратите внимание, что в приближении для данного значения объема потока увеличение размера воздуховода (скажем, со 100 мм до 120 мм) уменьшит потери на трение в 3 раза.
| 0,082 | 0,245 | 0,816 | |||||
| кг / м 2 / с 2 | |||||||
| Размер воздуховода | Q | Q | Q | ||||
|---|---|---|---|---|---|---|---|
| в | мм | CFM | м 3 / с | CFM | м 3 / с | CFM | м 3 / с |
| 2½ | 63 | 3 | 0,0012 | 5 | 0,0024 | 10 | 0,0048 |
| 3¼ | 80 | 5 | 0,0024 | 10 | 0,0046 | 20 | 0,0093 |
| 4 | 100 | 10 | 0,0045 | 18 | 0,0085 | 36 | 0,0171 |
| 5 | 125 | 18 | 0,0083 | 33 | 0,0157 | 66 | 0,0313 |
| 6 | 160 | 35 год | 0,0163 | 65 | 0,0308 | 129 | 0,0611 |
| 8 | 200 | 64 | 0,0301 | 119 | 0,0563 | 236 | 0,1114 |
| 10 | 250 | 117 | 0,0551 | 218 | 0,1030 | 430 | 0,2030 |
| 12 | 315 | 218 | 0,1031 | 407 | 0,1919 | 799 | 0,3771 |
| 16 | 400 | 416 | 0,1965 | 772 | 0,3646 | 1513 | 0,7141 |
| 20 | 500 | 759 | 0,3582 | 1404 | 0,6627 | 2743 | 1,2945 |
| 24 | 630 | 1411 | 0,6657 | 2603 | 1,2285 | 5072 | 2,3939 |
| 32 | 800 | 2673 | 1,2613 | 4919 | 2,3217 | 9563 | 4,5131 |
| 40 | 1000 | 4847 | 2,2877 | 8903 | 4.2018 | 17270 | 8,1504 |
| 48 | 1200 | 7876 | 3,7172 | 14442 | 6,8161 | 27969 | 13,2000 |
Обратите внимание, что для представленных здесь диаграммы и таблицы поток находится в турбулентной, гладкой области трубы с R * Примечания
Потери напора на трение по длине трубопровода



Равномерное движение жидкости наблюдается в тех случаях, когда живое сечение по длине потока постоянно (например, в напорных трубах постоянного диаметра).
Пи равномерном движении в трубах потери напора на трение hтр или по длине 

а для труб любой формы сечения по формуле

В некоторых случаях используют также формулу

Потери давления на трение по длине определяются по формуле
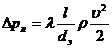
λ— коэффициент гидравлического трения (безразмерный);
l, d, υ, R, dэ — соответственно длина участка трубы или канала, диаметр трубы, средняя скорость течения, гидравлический радиус и эквивалентный диаметр;


Размерность коэффициента Шези м 1/2 /с.
Коэффициент гидравлического трения λ учитывает влияние на потерю напора по длине всех факторов, которые не получили отражения в формулах (3.1) и (3.4), но существенны для определения гидравлических сопротивлений. Важнейшими из этих факторов являются вязкость жидкости и состояние стенок трубы.
Эквивалентная шероховатость (кэ) различных труб Таблица 3.1
| Материал и вид трубы | Состояние трубы | kэ , мм * |
| Тянутые трубы из стекла и цветных металлов | Новые, технически гладкие | 0-0.002/0.001 |
| Бесшовные стальные трубы | Новые и чистые, тщательно уложенные После нескольких лет эксплуатации | 0.01-0.02/0.014 0.15-0.3/0.2 |
| Стальные трубы сварные | Новые и чистые С незначительной коррозией Умеренно заржавевшие Старые заржавевшие Сильно заржавевшие или с большими отложениями | 0.03-0.1/0.06 0.1-0.2/0.15 0.3-0.7/0.5 0.8-1.5/1 2-4/3 |
| Клепанные стальные трубы | Легко клепанные Сильно клепанные | 0.5-3 До 9 |
| Оцинкованные железные трубы | Новые и чистые После нескольких лет эксплуатации | 0.1-0.2/0.15 0.4-0.7/0.50 |
| Чугунные трубы | Новые асфальтированные Новые без покрытия Бывшие в употреблении Очень старые | 0-0.16/0.012 0.2-0.5/0.3 0.5-1.5/1 До 3 |
| Деревянные трубы | Из деревянных клепок, тщательно оструганных Из обычных деревянных клепок Из необструганных досок | 0.1-0.3/0.15 0.3-1/0.5 1-2.5/2 |
| Фанерные трубы | Новые | 0.02-0.05/0.03 |
| Асбестоцементные трубы | » | 0.05-0.1/0.085 |
| Бетонные трубы | Новые из предварительно напряжнного бетона Новые центробежные Бывшие в употреблении Из необработанного бетона | 0-0.05/0.03 0.15-0.3/0.2 0.3-0.8/0.5 1-3 |
* После дроби даны средние значения.
Для турбулентного и ламинарного течения применяются различные формулы для определения коэффициента гидравлического трения.
Для определения коэффициента гидравлического трения λ при турбулентном течении в чопорных трубопроводах рекомендуются следующие формулы:
1) формула Колбрука

2) формула А. Д. Альтшуля

Формулы (3.6) и (3.7.) Получены с помощью полуэмпирической теории турбулентности [1] и действительны для всех однородных ньютоновских жидкостей. Расхождение между формулами (3.6) и (3.7) практически не превышает 2—3%.
Значения λ, вычисленные по формуле (3.7), могут быть найдены также по номограмме. По данным А. Д. Альтшуля при значении критерия зоны турбулентности

формула (3.6) приводится к формуле Прандтля — Никурадзе:

а формула (3.7) — к формуле Б. Л. Шифринсона:

Обе последние формулы справедливы для так называемых вполне шероховатых труб, сопротивление которых не зависит от числа Рейнольдса. В табл. 3.3 приведены значения λ, подсчитанные по формуле (3.10).
| k/d | 0,025 | 0,01 | 0.005 | 0,0025 | 0,00125 | 0,00084 | 0,00063 | 0.0005 | 0,00033 | 0,00025 |
| λ | 0.0437 | 0,0350 | 0,0294 | 0,0247 | 0.0208 | 0,0188 | 0.0175 | 0,0165 | 0.0150 | ,0139 |
При значении критерия зоны турбулентности

формула (3.6) приводится к формуле Прандтля — Никурадзе:

а формула (3.7) – к формуле Блазиуса:
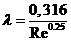
Эти формулы справедливы для гидравлически гладких труб, сопротивление которых не зависит от шероховатости.
которая действительна при Rе>920 000, и

где d—диаметр трубы, м;
ν— кинематическая вязкость жидкости, м 2 /с;
υ— средняя скорость течения, м/с.
Формулы (3.14) и (3.15) рекомендуется применять для расчета стальных и чугунных водопроводных труб больших диаметров (d = 600-—1200 мм) с учетом увеличения их сопротивления в процессе эксплуатации.
При определении коэффициента гидравлического трения для труб некруглого сечения можно пользоваться приведенными выше формулами, подставляя в них вместо диаметра d эквивалентный диаметр dэ или учетверенный гидравлический радиус 4R. При этом, например, формула (3.7) принимает вид
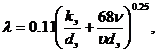

Найденное по этим формулам значение λ следует подставить в формулу (3.2) для определения потерь напора по длине.
Ламинарное течение. При ламинарном течении в круглых трубах коэффициент гидравлического трения вычисляют по формуле

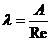
где А — коэффициент, численное значение которого зависит от формы поперечного сечения трубы, а число Рейнольдса определяется по формуле
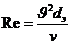
Значения коэффициента формы А и эквивалентного диаметра для труб с различной формой поперечного сечения приведены в приложении 17.
Подставляя формулу (3.18) в выражение (3.1), получаем зависимость для определения потерь напора по длине при ламинарном движении в круглых трубах в виде

Формула (3.21) получена теоретически Пуазейлем. В соответствии с этой формулой 
Примеры 3
Пример 3.1. Вентиляционная труба d =0,1 м (100 мм) имеет длину l=100 м
. Определить давление, которое должен развивать вентилятор, если
расход воздуха, подаваемый по трубе, Q=0,О78 м 3 /с. Давление на выходе р= pатм =101 кПа, Местных сопротивлений по пути не имеется. Температура воздуха 20°С.
Решение. Находим скорость воздуха в трубе:

Относительная шероховатость (по табл. З.1 kэ=0,2 мм)
Коэффициент гидравлического трения
λ =0,11 (kэ/d+68Rе) 0’25 =0,11 (0,002+0,001) 0.2 5 =0.0256.
По формуле (3.4) находим потери давления на трение (р=I,18 кг/м 3 ):
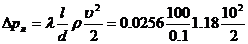
Пример 3.2. Расход воды при температуре 10 0 С в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических оцинкованных стальных труб (при kэ=0,15 мм),Q =0,0075 м 3 /с. Внутренняя труба имеет наружный диаметр d=0,075 м, а наружная труба имеет внутренний диаметр D =0,1 м. 1-Iайти потери напора на трение на длине трубы l=300 м.
Решение. Площадь живого сечения
Смоченный периметр живого сечения
χ= π (0,075+0,1)=3,14*0,I75 =0,55 м.
Решение. Вычислим число Рейнольдса для каждой ветви системы гидропередачи, учитывая, что скорость
В обеих магистралях режим течения ламинарный.
Коэффициент гидравлического трения находим по формуле (3.18):
Потери давления в каждой ветви определим по формуле (3.4):
Пример 348. Определить расход воды в бывшей в эксплуатации водопроводной
трубе диаметром d= 0,3 м. если скорость на оси трубы, замеренная
трубкой Пито—Прандтля, имакс=4,5 м/с, а температура воды 10°С.
Решение. Находим по табл. 3.1 значение абсолютной шероховатости для
старых стальных труб: kэ=0,5 мм.
Предполагая, что движение воды происходит в квадратичной области
турбулентного движения, определяем коэффициент гидравлического трения по
сокращенной формуле (3.10):
Среднюю скорость определяем по уравнению (3.25):
имакс/ 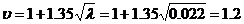
Определяем значения критерия зоны турбулентности по формуле (3.8):
Таким образом, движение действительно происходит в квадратичной области сопротивления.



.svg/220px-Equal-friction_chart_for_air_in_metal_duct_(%CE%B5_%3D_0.05mm).svg.png)