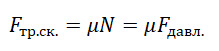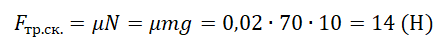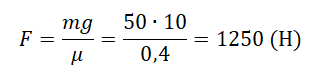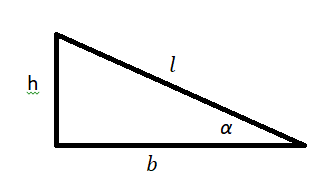Чем обусловлено трение скольжения

Сила трения

Что такое сила трения

Что такое сила трения?

Трение возникает вследствие взаимодействия между атомами и молекулами тел, когда они соприкасаются друг с другом.

Как и для любого другого взаимодействия, для трения справедлив третий закон Ньютона. Если на одно из двух взаимодействующих тел действует сила трения, то такая же по модулю сила действует на другое тело в противоположном направлении.

Сила трения покоя и сила трения скольжения

Различают сухое и вязкое трение, силу трения покоя, силу трения скольжения, силу трения качения.

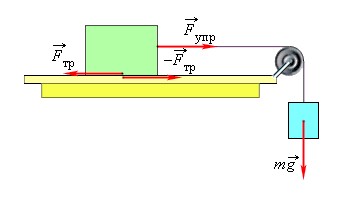
Представим, что на тело, например, брусок, лежащий на столе, действует некоторая внешняя сила. Эта сила стремится сдвинуть брусок с места. Пока тела покоятся, на брусок действуют сила трения покоя и, собственно, внешняя сила. Сила трения покоя равна внешней силе и уравновешивает ее.

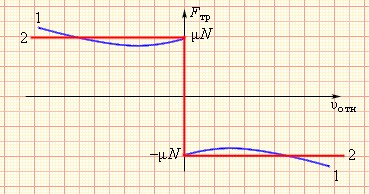
При решении физических задач силу трения скольжения часто принимают равной максимальной силе трения покоя, а зависимостью от силы трения от относительной скорости движения тел пренебрегают.

На рисунке выше показаны реальная и идеализированная характеристики сухого трения. Как видим, на самом деле сила трения скольжения меняется в зависимости от скорости, однако изменения не столь велики, чтобы ими нельзя было пренебречь.

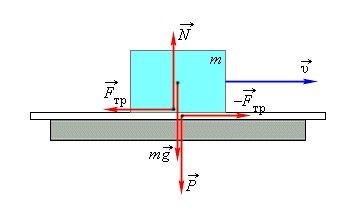
Сила трения пропорциональна силе нормальной реакции опоры.

Что такое коэффициент трения скольжения?

Силы трения качения возникают при качении тел. Обычно при решении задач ими пренебрегают.

Вязкое трение в жидкостях и газах

Вязкое трение возникает при движении тел в жидкостях и газах. Сила вязкого трения также направлена в сторону, противоположную движению тела, но по величине гораздо меньше силы трения скольжения. Трение покоя отсутствует при вязком трении.

Например, силы вязкого трения в воде и масле будут отличаться, так как эти жидкости имеют различные вязкости.

Источник

Чем обусловлено трение скольжения

Трение скольжения является наиболее распространенным видом трения. Основной характеристикой трения скольжения является сила трения.

(1)

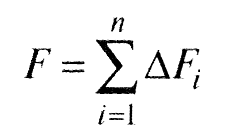
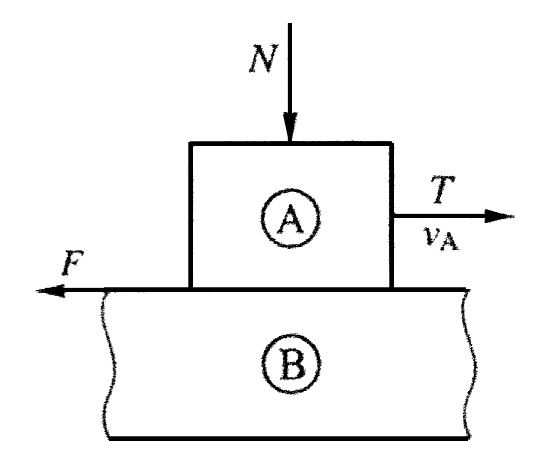
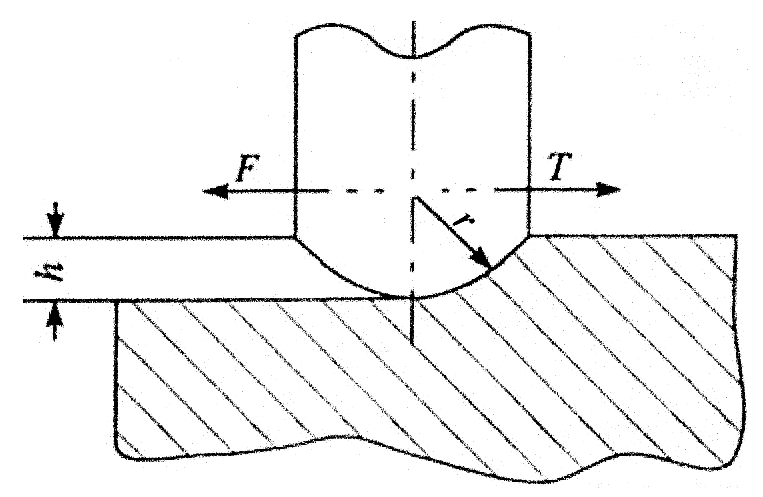
Схема контакта трущихся тел при трении скольжения приведена на рис.1. Сила трения направлена противоположно направлению относительного движения контактирующих тел.

При переходе от состояния покоя к состоянию движения имеет место состояние предварительного смещения.

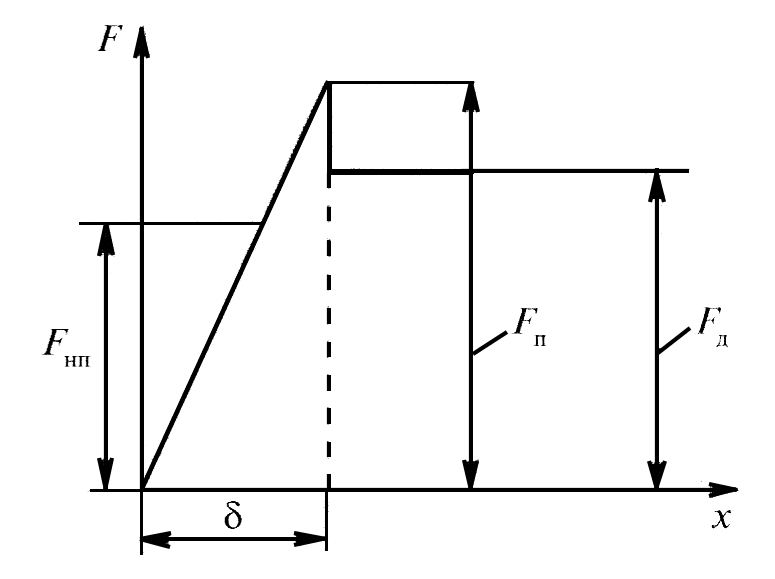
В соответствии с существованием трения покоя и трения движения различают силу трения покоя и силу трения движения, количественно оценивающие эти процессы. Изменение силы трения при переходе от покоя к движению контактирующих тел по мере перемещения одного тела относительно другого иллюстрирует рис.2. При трогании неподвижного тела с места движению предшествует стадия предварительного смещения.

Рис.2. Изменение силы трения в зависимости от величины перемещения x.

Развиваемая по мере увеличения микросмещения неполная сила трения покоя F_нп возрастает до тех пор, пока не будет достигнута полная сила трения F_п, превышение которой ведет к началу макросмещения, т.е. трение покоя скачкообразно сменяется трением движения F_д и начинается непрерывное перемещение одного тела относительно другого. Имеет первоначально упругий характер, т.е. прекращение действия сдвигающей силы T (см. рис.1) ведет к возврату в положение равновесия.

Развиваемая при микросмещении полная сила трения покоя для несмазываемых тел F_п почти всегда выше силы трения движения F_д.

Законы Амонтона для трения скольжения

При рассмотрении процесса трения скольжения в качестве первого приближения используют экспериментально установленные еще Амонтоном (1699) закономерности, известные в литературе как законы Амонтона.

1. Сила трения F пропорциональна усилию N, сжимающему трущиеся тела в направлении, нормальном к поверхности трения (Поверхностью трения называют номинальную поверхность твердого тела, по которой осуществляется взаимодействие твердых тел при внешнем трении)

2. Сила трения не зависит от номинальной площади контакта трущихся твердых тел.

В процессе развития триботехники было установлено, что область применения законов Амонтона ограничена. Так, независимость коэффициента трения от нагрузки, следующая из приведенного уравнения, нарушается в области очень малых и достаточно больших нагрузок. Закон Амонтона нарушается также для очень твердых тел (алмаз) и очень упругих тел (резина). Коэффициент трения этих материалов уменьшается с увеличением нагрузки. Номинальная площадь контакта трущихся тел может влиять на величину силы трения для материалов, обладающих вязкоупругими свойствами, а также в тех случаях, когда она оказывает влияние на поступление среды в трибоконтакт.

Механизм внешнего трения

В общем случае коэффициент трения зависит от большого числа факторов (напряженно-деформированного состояния фрикционного контакта, механических и физико-химических свойств поверхностного слоя контактирующих тел, окружающей среды, в том числе смазочного материала, конструктивных особенностей сопряжения, режима работы узла трения и т.д.) и определяется в основном взаимодействием поверхностных слоев твердых тел, вовлеченных в трибологический контакт, между собой и взаимодействием рабочих поверхностей твердых тел со средой, включая смазочный материал.

Взаимодействие твердых тел в процессе трения развивается в микрообъемах, образующихся в зоне касания этих тел. По И.В. Крагельскому, в местах касания возникают фрикционные связи (т.е. пятна контакта, которые образуются и существуют лишь при совместном действии нормальных и тангенциальных сил в фрикционном контакте), образующие некоторое «третье тело». Это третье тело включает в себя измененный материал обоих контактирующих тел, наделенный своим химическим составом, напряженным состоянием и структурой. И.В. Крагельский при анализе трибологического процесса выделяет три этапа:

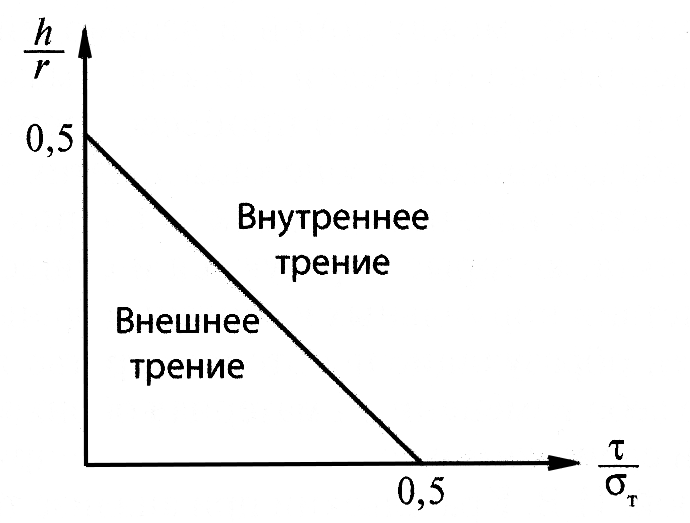
В том случае, если разрыв фрикционных связей происходит внутри «третьего тела», имеет место внешнее трение. При этом должно соблюдаться такое соотношение прочностных свойств «третьего тела» и свойств материала трущихся тел в объеме, при котором прочность на сдвиг возрастает по мере удаления от поверхности вглубь основного материала (сформулированное И.В. Крагельским правило положительного градиента механических свойств по глубине, характеризуемое отношением dτ_кр/dτ>0). При этом важно не только соотношение сдвиговых прочностей в тончайшем поверхностном слое ( «третье тело») и в объеме тел, но и геометрические характеристики трибологического контакта (безразмерная глубина зоны деформации). Это соотношение называется порогом внешнего трения. Для сферической модели неровностей это соотношение имеет вид:

(3)

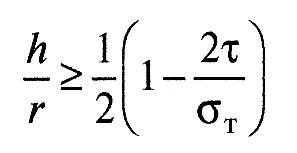
При нарушении этого соотношения имеет место переход от внешнего трения к внутреннему, характеризуемому интенсификацией разрушения поверхностных слоев контактирующих тел.

Распределение областей локализации внешнего и внутреннего трения иллюстрирует рис.3.

Рис.3. Области локализации внешнего и внутреннего трения (по Польцеру и Майснеру)

На процесс внешнего трения влияет большое количество факторов. но в конечном счете основную роль играет взаимодействие твердых тел между собой на участках трибологического контакта. Это взаимодействие заключается в преодолении сил молекулярного притяжения (адгезии) между контактирующими телами на пятнах (элементарных участках) площади фактического контакта, а также в формоизменении рельефа контактирующих тел в результате их упругих и пластических деформаций их поверхностных слоев. Таким образом, трение определяется процессами деформации поверхностных слоев и адгезией контактирующих тел в результате их межмолекулярного взаимодействия.

Согласно молекулярно-механической теории И.В. Крагельского, силу трения можно рассматривать как сумму адгезионной и деформационной составляющих

Расчет коэффициента трения

Наиболее распространенной характеристикой процесса трения является величина коэффициента трения f, равная отношению силы трения F двух тел к нормальной силе N, прижимающей эти тела друг к другу. В таком случае

(5)

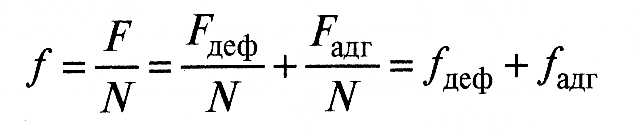
Расчет коэффициента трения при контакте единичной неровности, сводится к определению его деформационной и адгезионной составляющих.

Деформационная составляющая для единичного контакта определяется глубиной относительного внедрения h/r, т.е. отношения глубины h внедрения сферической неровности к радиусу r этой неровности (рис.4). Значение деформационной составляющей рассчитывают для пластического контакта единичной неровности с деформируемым телом по формуле:

(6)

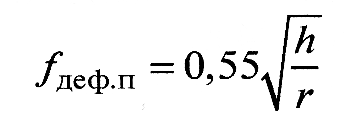
Рис.4. Схема и вычисление деформационной составляющей коэффициента трения.

и для упругого контакта этого сопряжения по формуле:

(7)

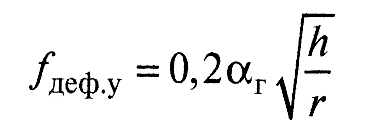
Адгезионная составляющая коэффициента трения подчиняется биноминальному закону:

(8)

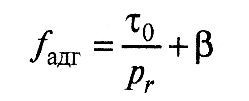
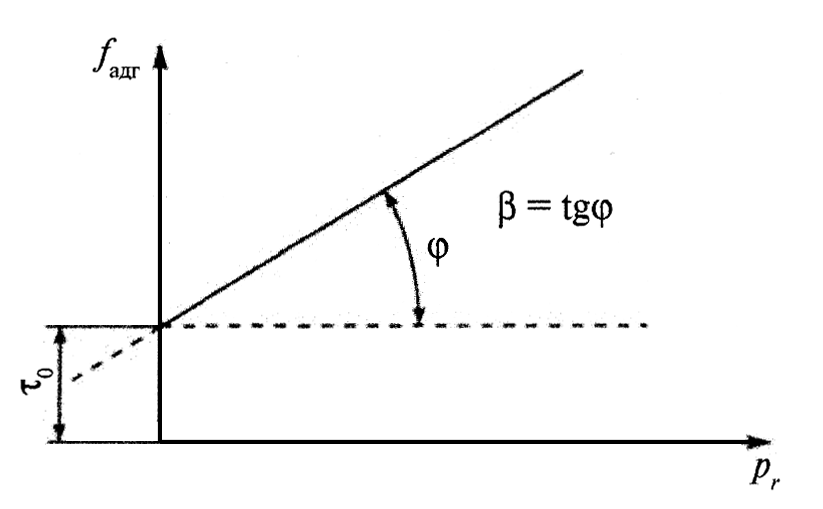
Биноминальный закон трения следует из представления о существовании «третьего тела», которое в процессе трения находится в состоянии непрерывного формоизменения, «течет» подобно жидкости в узком зазоре между двумя телами, перемещающимися одно относительно другого. При этом исходят из допущения пропорциональности сопротивления сдвигу единичной частицы «третьего тела» и времени ее оседлой жизни по уравнению Френкеля-Журкова (рис.5).

Следует иметь в виду, что в несколько иной форме и из совершенно иных представлений биноминальный закон трения был выведен Б.В. Дерягиным еще в 1934 г.

Рис.5. Зависимость адгезионной составляющей коэффициента трения (удельного сдвигового сопротивления) и f_адг от фактического давления p_r.

Определение величин τ 0 и β производится экспериментально.

Значения τ 0 и β для ряда распространенных материалов табулированы (табл.1). Это позволяет рассчитывать коэффициенты трения этих материалов для различных условий контакта и разной микрогеометрии поверхностей контактирующих тел.

Таблица 1. Параметры сдвиговой прочности молекулярных связей при трении по закаленной стали (по И.В. Крагельскому и Н.М. Михину)

№ п/п	Материал	τ 0, МПа	β
1	Свинец	3,6	0,057
2	Серебро	10,0	0,081
3	Медь	15,0	0,08
4	Олово	5,0	0,068
5	Индий	1,5	0,066

Для приработанных поверхностей коэффициент трения не зависит от нагрузки и может быть рассчитан из уравнения:

(9)

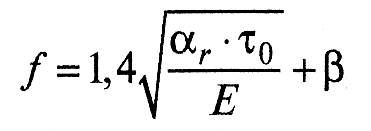
Интересно отметить, что, согласно Ю.Н. Васильеву, коэффициент β характеризует долю работы сил трения, затраченной на изнашивание трущихся тел.

Таким образом, суммарный коэффициент трения на единичном пятне контакта

(10)

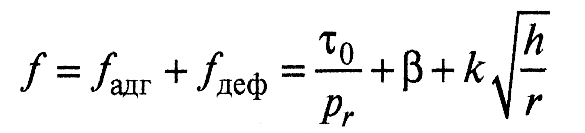
Расчет коэффициента трения для множественного контакта. Для ансамбля неровностей силы трения на единичных пятнах контакта суммируются и для множественного контакта силы трения рассчитывают по формуле:

(11)

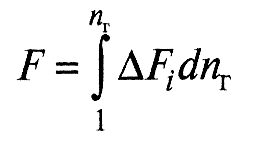
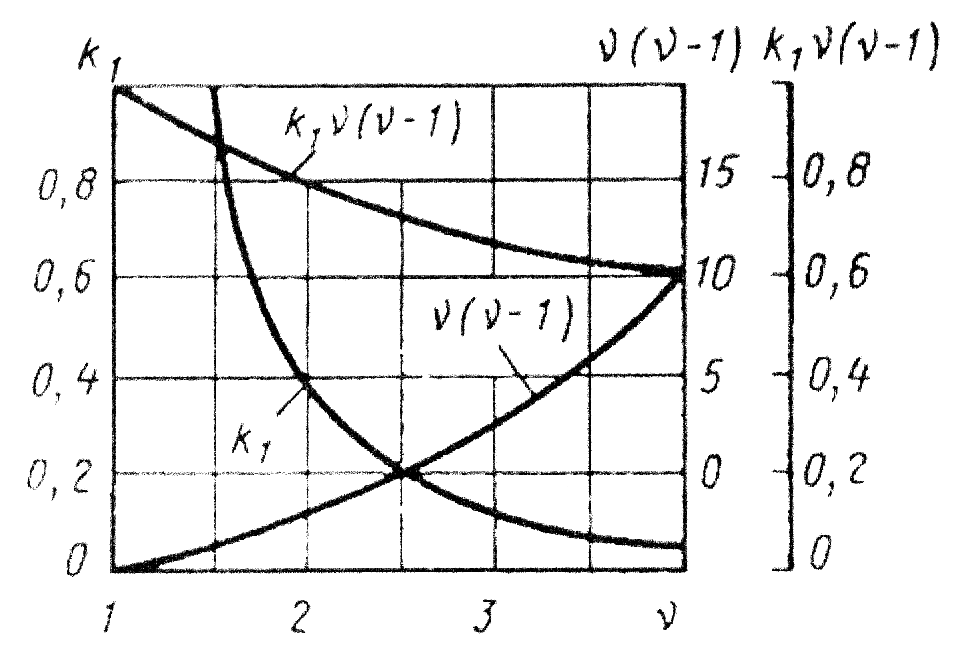
После ряда подстановок и несложных преобразований отсюда получены уравнения для расчета коэффициента трения при различных видах фрикционного контакта. Такое уравнение имеет вид:

(12)

(13)

(14)

(15)

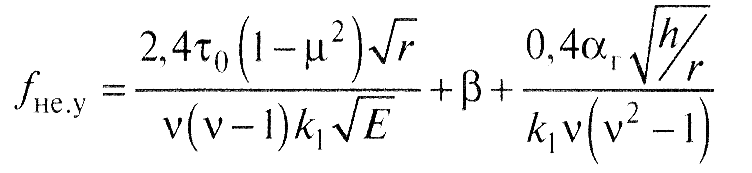
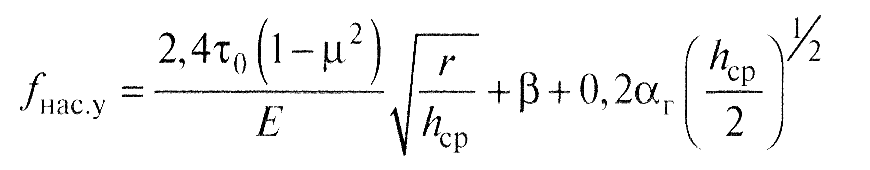
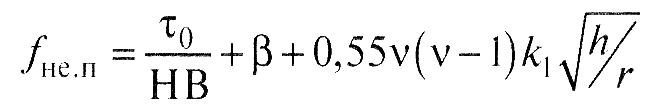
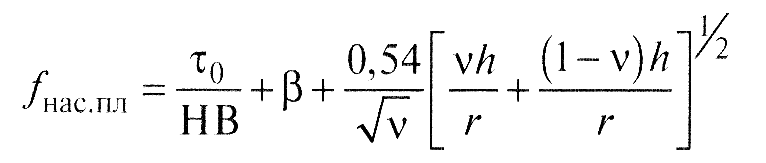
Рис.6. График для определения значений k_1′ν(ν-1) и k₁ν(ν-1) в зависимости от параметра ν.

Для приработанных поверхностей трение происходит в условиях упругого контакта; коэффициент трения при этом не зависит от нагрузки:

(16)

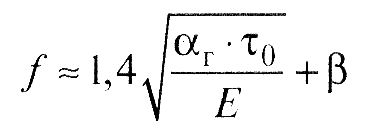
Факторы влияющие на трение скольжения.

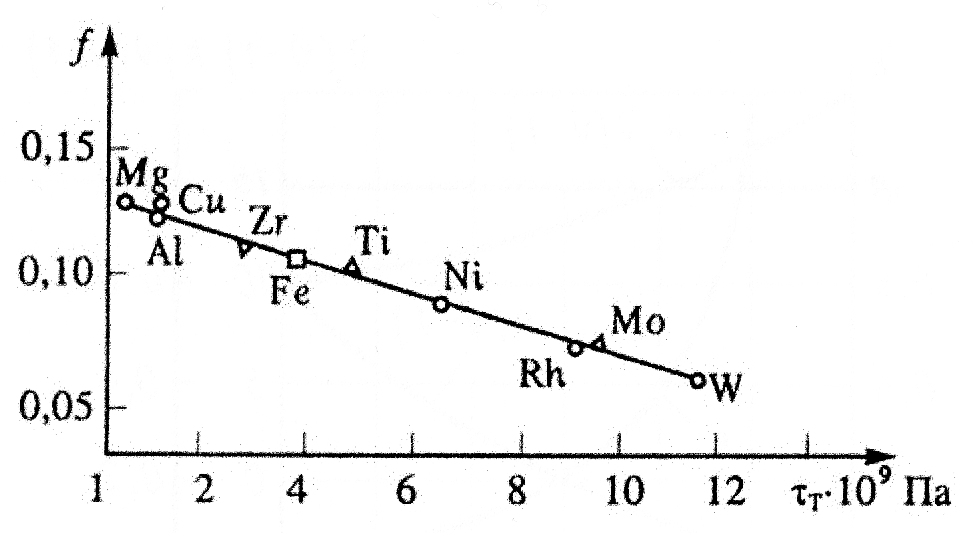
2. Значительное влияние на коэффициент трения оказывают строение и физико-механические свойства контактирующих тел. Так, у одноименных металлов с кристаллической кубической решеткой (Al-Al; Cu-Cu; Fe-Fe) коэффициент трения выше, чем у металлов с гексагональной упаковкой (Cd-Cd; Mn-Mn; Zn-Zn) (рис.7).

Рис.7. Зависимость коэффициента трения f от предела текучести на сдвиг τ_т для различных металлов.

3. Для пар трения из различных металлов коэффициент трения ниже, чем для одинаковых.

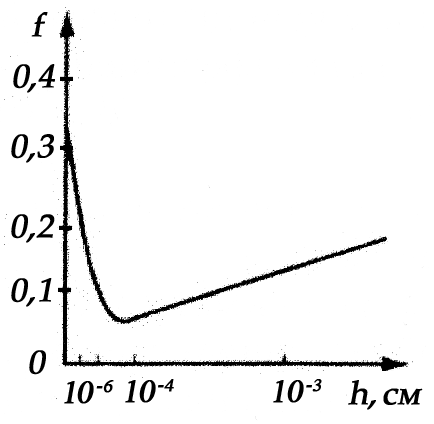
4. На коэффициент трения материалов значительное влияние оказывают природа образующихся на поверхности «вторичных структур» (например, оксидных пленок и т.д.) или заранее нанесенных тонких покрытий. Важно соотношение физико-механических свойств покрытия и подложки. Если металл мягок и эластичен, а оксид тверд и хрупок, то пленки легко разрушаются, и имеет место ювенальный контакт при малых нагрузках. Если металл имеет такие же деформационные свойства, как и его оксид, то эта пленка деформируется вместе с металлом не разрушаясь (например, Cu), обеспечивает снижение адгезионного эффекта и препятствует преодолению внешнего трения. Для обеспечения низкого коэффициента трения необходимо, чтобы поверхностная пленка обеспечивала полное разделение контактирующих поверхностей (обеспечение правила положительного градиента прочности по глубине), но не должна быть излишне толстой, чтобы избежать повышения деформационной составляющей коэффициента трения, так как в толстой пленке деформационная составляющая коэффициента трения становится заметной. На рис.8 это показано применительно к зависимости коэффициента трения закаленной стали по стали, покрытой пленкой индия, от толщины этого покрытия.

Рис.8. Зависимость коэффициента трения f стального сферического индентора радиусом 0,3 мм по инструментальной стали, покрытой пленкой индия, от толщины h этого покрытия.

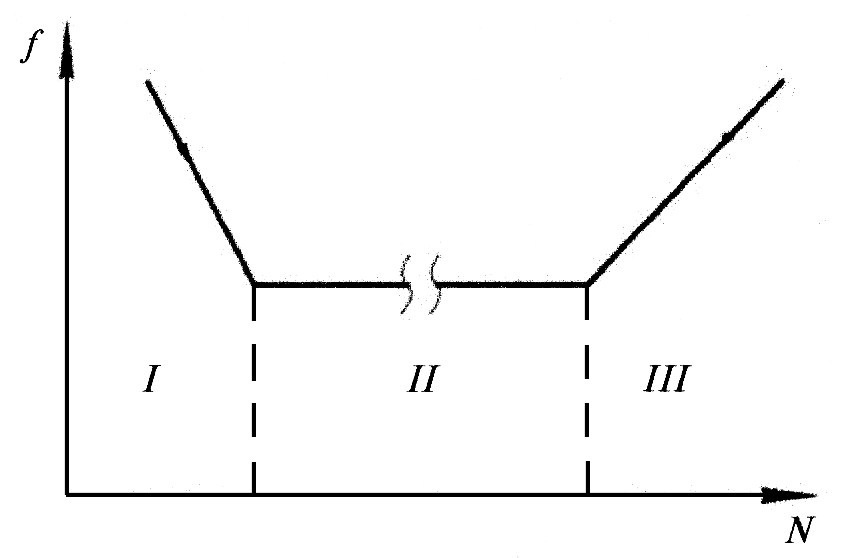
Образование и разрушение вторичных структур оказывает большое влияние на коэффициент трения. Так, на зависимости коэффициента трения, согласно Б.И. Костецкому, можно выделить три участка (рис.9): участок I, на котором коэффициент трения достаточно высок, но по мере повышения нагрузки по ряду причин (в частности, вследствие активации поверхностей трения, облегчающей образование вторичных структур в трибологическом контакте) снижается до некоторой установившейся величины (переходный режим). На участке II зависимость f(N) трение подчиняется закону Амонтона, вследствие образования на поверхности трения вторичных структур, обеспечивающих наличие положительного градиента механических свойств по глубине. Участок II ограничен некоторой критической нагрузкой, при которой скорость разрушения вторичных структур превысит скорость их образования, так что правило И.В, Крагельского перестает выполняться, и имеет место переход к схватыванию, заеданию и другим патологическим процессам вплоть до сваривания контактирующих поверхностей, т.е. режим повреждаемости.

Вследствие этого на участке III зависимости f(N) наблюдается резкий рост коэффициента трения, его скачкообразное изменение, поскольку при этом чередуется схватывание контактирующих поверхностей, разрушение образовавшихся при этом адгезионных соединений, проскальзывание и т.д.

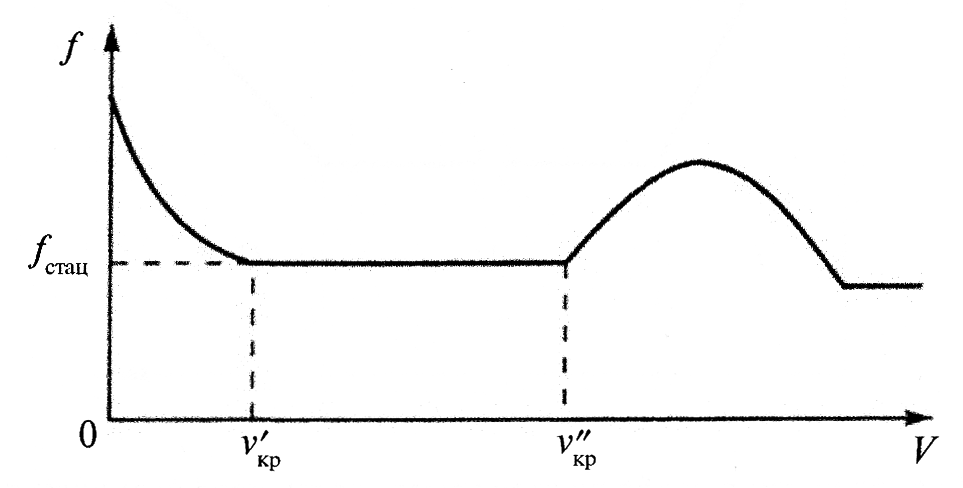
Рис.10. Схема изменения коэффициента трения f от скорости V относительного перемещения твердых тел.

Стационарный участок имеет место в диапазоне скоростей V’_кр и V»_кр, т.е. V’_кр ≤ 0 ≤ V»_кр, схватывание I рода имеет место при φ V’_кр, схватывание II рода происходит при V > V»_кр.

Схватывание I рода возникает при трение скольжения с малыми скоростями относительного перемещения и удельными нагрузками, превышающими предел текучести на участках фактического контакта при отсутствии слоя смазочного материала или вторичных структур, разделяющих поверхности трения. Схватывание II рода также является процессом недопустимой повреждаемости поверхностей трения, выражающейся в образовании местных очагов схватывания, сваривания, причем этот процесс обусловлен размягчением, деформацией и контактированием ювенильных поверхностей трущихся тел. Этот процесс возникает при трении скольжения с большими скоростями и удельными нагрузками. Значительное тепловыделение может привести к существенному размягчению поверхностей и даже к их оплавлению, так что между трущимися телами может образоваться прослойка расплавленного металла, в результате чего трение даже снижается (участок справа от участка III на рис.10). На стационарном участке сила трения практически не изменяется во времени, на участках I и III сила трения скачкообразно изменяется во времени.

Зависимость f = φ(V) может при изменении условий процесса смещаться вверх или вниз, а стационарный участок может расширяться или сужаться, что определяется условиями образования вторичных структур, обеспечивающих существование стационарного участка.

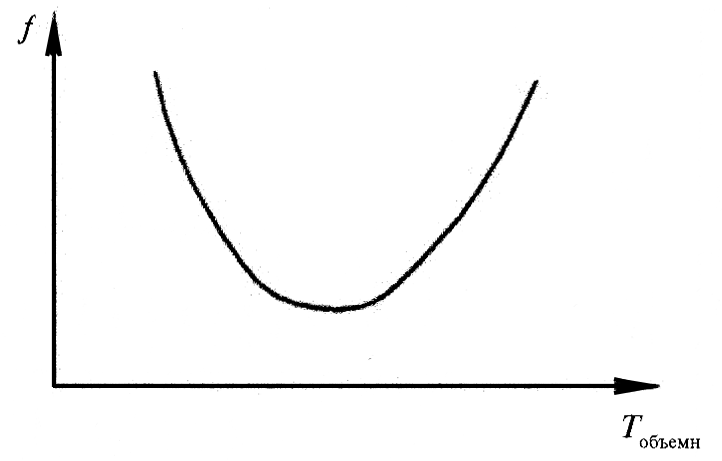
Рис.11. Влияние объемной температуры на коэффициент трения.

Источник

Сила трения

теория по физике 🧲 динамика

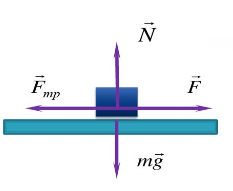
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.

Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как F _тр. Единица измерения — Н (Ньютон).

Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.

Виды сухого трения:

Трение скольжения

Сила трения скольжения определяется формулой:

μ — коэффициент трения, N — сила реакции опоры, F_давл. — сила нормального давления

Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.

Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.

Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.

Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.

Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?

Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:

Трение покоя

Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).

Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:

Способы определения вида силы трения, возникающей между телами, и ее модуля:

Проекция на ось ОХ:

Проекция на ось ОУ:

Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости

Второй закон Ньютона в векторной форме:

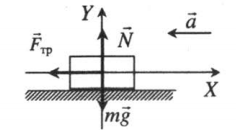
Проекция на ось ОХ:

Проекция на ось ОУ:

Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх)

Второй закон Ньютона в векторной форме:

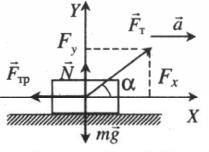
Проекция на ось ОХ:

Проекция на ось ОУ:

Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз)

Второй закон Ньютона в векторной форме:

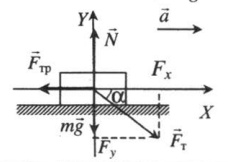
Проекция на ось ОХ:

Проекция на ось ОУ:

Внимание! В случаях, когда сила тяги F _т направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.

Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения? 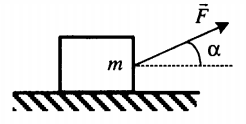Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:

Проекция сил на ось ОУ выглядит так:

Отсюда силы реакции опоры равна:

Подставим ее в формулу для вычисления силы трения и получим:

Движение тела по вертикальной плоскости

Тело прижали к вертикальной плоскости и удерживают

Второй закон Ньютона в векторной форме:

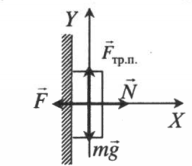
Проекция на ось ОХ:

Проекция на ось ОУ:

Тело поднимается под действием силы тяги, направленной под углом к вертикали

Второй закон Ньютона в векторной форме:

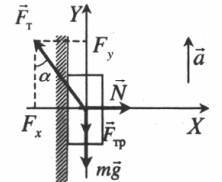
Проекция на ось ОХ:

Проекция на ось ОУ:

Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя. Проекция на ось ОХ:

Отсюда следует, что сила должна быть равна силе реакции опоры. Проекция на ось ОУ:

Перепишем, выразив силу трения через силу реакции опоры:

Отсюда выразим силу реакции опоры: 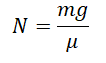Следовательно:

Движение тела по наклонной плоскости

Движение вниз без трения

Второй закон Ньютона в векторной форме:

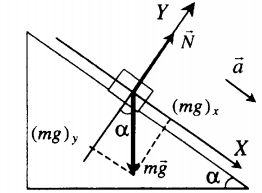
Тело покоится на наклонной плоскости

Второй закон Ньютона в векторной форме:

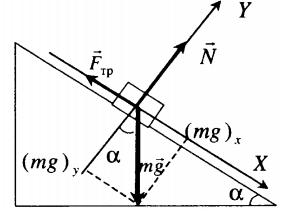
Тело удерживают на наклонной плоскости

Второй закон Ньютона в векторной форме:

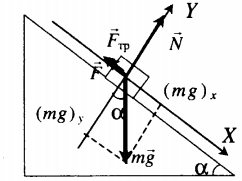
m g + N + F + F _тр = m a

Равноускоренное движение вверх с учетом силы трения

Второй закон Ньютона в векторной форме:

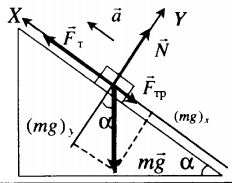
Равномерное движение вверх с учетом силы трения

Второй закон Ньютона в векторной форме:

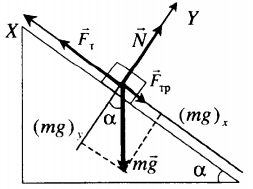
m g + N + F + F _тр = m a

Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам. Переведем массу в килограммы: 200 г = 0,2 кг. Проекция сил, действующих на тело, на ось ОХ:

Отсюда сила трения равна:

Подставляем известные данные и вычисляем:

Полезная информация

Косинус угла наклона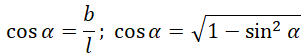
Синус угла наклона (уклон)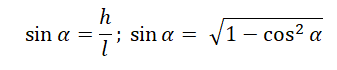
Тангенс угла наклона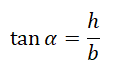

При исследовании зависимости силы трения скольжения F тр от силы нормального давления F д были получены следующие данные:

Источник