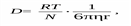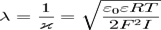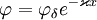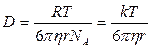Чем обусловлено броуновское движение частиц в коллоидных системах

Молекулярно-кинетические свойства коллоидных систем: броуновское движение, диффузия, осмотическое давление.

К молекулярно-кинетическим свойствам свободнодисперсных систем относятся: броуновское движение, диффузия, осмотическое давление, седиментация.
Броуновское движение проявляется хаотическим непрерывным движением частиц дисперсной фазы под действием ударов молекул растворителя (дисперсионной среды), находящихся в состоянии интенсивного молекулярно-теплового движения. Перемещаться частицы могут в различных направлениях. Траектория их движения представляет собой ломаную линию неопределенной конфигурации (рис.31).

К оличественной мерой перемещения частицы при броуновском движении является величина её среднего смещения за некоторый промежуток времени. Смещением или сдвигом частицы называют расстояние между проекциями начальной (1) и конечной (2) точек траектории на ось смещений. А.Эйнштейн и М.Смолуховский установили, что квадрат среднего смещения равен:

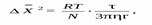
где ΔX – среднее смещение частицы, м –1 ; R – газовая постоянная, равная 8,31 Дж×моль/К; Т – температура, К; N – число Авогадро, моль –1 ; τ – время смещения, с; η – вязкость дисперсионной среды, Н×c/м 2 ; r – радиус дисперсной частицы, м.Из этого уравнения следует, что броуновское движение тем интенсивнее, чем меньше размер частиц и вязкость среды и чем выше температура. Броуновское движение не прекращается со временем, т.е. не зависит от длительности существования системы.

Диффузия – это самопроизвольно протекающий процесс выравнивания концентраций ионов, молекул или коллоидных частиц вследствие их беспорядочного теплового (для истинных растворов) или броуновского (для дисперсных систем) движения. Диффузия заканчивается с достижением равномерного распределения частиц по всему объему. Следовательно, диффузия возможна лишь в системах с неодинаковыми концентрациями.Величина, показывающая количество вещества, диффундирующего через поперечное сечение площадью 1 м 2 за 1 секунду при градиенте концентраций равном 1, называется коэффициентом диффузии.По формуле Стокса–Эйнштейна коэффициент диффузии связан с размерами диффундирующих частиц уравнением:

где D – коэффициент диффузии, м 2 /с.
Из этого уравнения следует, что чем больше размер частиц и выше вязкость среды, тем меньше скорость диффузии. Следовательно, при одинаковой температуре скорость диффузии в коллоидных растворах в сотни и тысячи раз меньше, чем в истинных растворах.
Осмотическое давление –одно из коллигативных свойств растворов, т.е. зависит только от количества свободно движущихся частиц. Следовательно, оно характерно, как для коллоидных растворов, так и для истинных, и для расчета величины осмотического давления коллоидных растворов также можно применить уравнение Вант-Гоффа:
Р_осм. = ,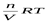
где Р_осм. – осмотическое давление золя, Па; n – количество частиц, моль; V– объем золя, м 3 ; R– газовая постоянная; Т– температура, К.
Если учесть, что объем и масса коллоидной частицы значительно больше, чем объем и масса молекулы низкомолекулярных веществ, то при одной и той же массовой концентрации вещества, в единице объема золя содержится значительно меньше частиц, чем в единице объема истинного раствора. Поэтому осмотическое давление коллоидных растворов ничтожно мало по сравнению с таковым в истинных растворах. Например, осмотическое давление золя золота с массовой концентрацией вещества 10 г/л равно 45 Па, а раствора сахарозы той же концентрации и в тех же условиях – 72500 Па.
Второй особенностью осмотического давления коллоидных растворов является его непостоянство. В связи с термодинамической неустойчивостью коллоидных растворов в них непрерывно протекают процессы агрегации и дезагрегации, приводящие к изменению числа осмотически активных частиц в единице объема, а, следовательно, и осмотического давления.

75.Классификация коллоидных систем. Механизм возникновения электрического заряда коллоидной частицы. Строение двойного электрического слоя. Мицелла. Ядро. Гранула.

Двойной электрический слой (межфазный) (ДЭС) — слой ионов, образующийся на поверхности частиц в результате адсорбции ионов из раствора, диссоциации поверхностного соединения или ориентирования полярных молекул на границе фаз. Ионы, непосредственно связанные с поверхностью называются потенциалоопределяющими. Заряд этого слоя компенсируется зарядом второго слоя ионов, называемых противоионами.

В отсутствие теплового движения частиц, строение двойного электрического слоя подобно строению плоского конденсатора. Но в отличие от идеального случая, ДЭС в реальных условиях имеет диффузное (размытое) строение. Согласно современной теории структуру ДЭС составляют два слоя:Слой Гельмгольца или адсорбционный слой, примыкающий непосредственно к межфазной поверхности. Этот слой имеет толщину δ, равную радиусу потенциалопределяющих ионов внесольватированном состояниДиффузный слой или слой Гуи, в котором находятся противоионы. Диффузный слой имеет толщину λ, которая зависит от свойств системы и может достигать больших значений. Толщина диффузного слоя рассчитывается по формуле:

Электрической характеристикой ДЭС является потенциал φ. Существует несколько характеристических потенциалов:Потенциал диффузного слоя φ_δ, соответствующий границе адсорбционного и диффузного слоёв. Внутри диффузного слоя потенциал можно рассчитать по уравнению Гуи-Чепмена:

· Потенциал φ_x=λ, меньший, чем φ_δ в e раз и характеризующий толщину диффузного слоя.Электрокинетический потенциал или дзета-потенциал. Этот потенциал соответствует плоскости скольжения и является частью потенциала диффузного слоя. Плоскость скольжения образуется в результате того, что при движении дисперсных частиц наиболее удаленная часть диффузного слоя не участвует в движении, а остается неподвижной. Поэтому появляется нескомпенсированность поверхностного заряда частицы и становятся возможными электрокинетические явления. Дзета-потенциал является одной из важнейших характеристик двойного электрического слоя.

Дата добавления: 2016-01-16 ; просмотров: 3893 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Чем обусловлено броуновское движение частиц в коллоидных системах

Бро́уновское движе́ние — в естествознании, беспорядочное движение микроскопических, видимых, взвешенных в жидкости (или газе) частиц (броуновские частицы) твёрдого вещества (пылинки, крупинки взвеси, частички пыльцы растения и так далее), вызываемое тепловым движением частиц жидкости (или газа). Не следует смешивать понятия «броуновское движение» и «тепловое движение»: броуновское движение является следствием и свидетельством существования теплового движения.

Сущность явления

Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют),более мелкие частицы (менее 3мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.

Открытие броуновского движения

Это явление открыто Р. Броуном в 1827 году, когда он проводил исследования пыльцы растений. Шотландский ботаник Роберт Броун (иногда его фамилию транскрибируют как Браун) еще при жизни как лучший знаток растений получил титул «князя ботаников». Он сделал много замечательных открытий. В 1805 после четырехлетней экспедиции в Австралию привез в Англию около 4000 видов не известных ученым австралийских растений и много лет потратил на их изучение. Описал растения, привезенные из Индонезии и Центральной Африки. Изучал физиологию растений, впервые подробно описал ядро растительной клетки. Петербургская Академия наук сделала его своим почетным членом. Но имя ученого сейчас широко известно вовсе не из-за этих работ.
В 1827 Броун проводил исследования пыльцы растений. Он, в частности, интересовался, как пыльца участвует в процессе оплодотворения. Как-то он разглядывал под микроскопом выделенные из клеток пыльцы североамериканского растения Clarkia pulchella (кларкии хорошенькой) взвешенные в воде удлиненные цитоплазматические зерна. Неожиданно Броун увидел, что мельчайшие твердые крупинки, которые едва можно было разглядеть в капле воды, непрерывно дрожат и передвигаются с места на место. Он установил, что эти движения, по его словам, «не связаны ни с потоками в жидкости, ни с ее постепенным испарением, а присущи самим частичкам».
Наблюдение Броуна подтвердили другие ученые. Мельчайшие частички вели себя, как живые, причем «танец» частиц ускорялся с повышением температуры и с уменьшением размера частиц и явно замедлялся при замене воды более вязкой средой. Это удивительное явление никогда не прекращалось: его можно было наблюдать сколь угодно долго. Поначалу Броун подумал даже, что в поле микроскопа действительно попали живые существа, тем более что пыльца – это мужские половые клетки растений, однако так же вели частички из мертвых растений, даже из засушенных за сто лет до этого в гербариях. Тогда Броун подумал, не есть ли это «элементарные молекулы живых существ», о которых говорил знаменитый французский естествоиспытатель Жорж Бюффон (1707–1788), автор 36-томной Естественной истории. Это предположение отпало, когда Броун начал исследовать явно неживые объекты; сначала это были очень мелкие частички угля, а также сажи и пыли лондонского воздуха, затем тонко растертые неорганические вещества: стекло, множество различных минералов. «Активные молекулы» оказались повсюду: «В каждом минерале, – писал Броун, – который мне удавалось измельчить в пыль до такой степени, чтобы она могла в течение какого-то времени быть взвешенной в воде, я находил, в больших или меньших количествах, эти молекулы».

Теория броуновского движения

Построение классической теории

В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения. В частности, он вывел формулу для коэффициента диффузии сферических броуновских частиц:

Источник

Молекулярно-кинетические свойства коллоидных растворов (диффузия, броуновское движение, осмос).

Молекулярно-кинетическискими называются с-ва, обусловленные хаотическим тепловым движением частиц.

Кол. р-ры частный случай истинных р-ров. Д. фаза – растворенное в-во, д. среда – растворитель.

Броуновское движение беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа. Броуновское движение никогда не прекращается.

Интенсивность броуновского движения зависит от р-ров частиц, температуры и вязкости жидкости.

Частицы дисперсной фазы испытывают в единицу времени огромное число ударов со стороны молекул дисперсионной среды, находящихся в тепловом движении. в следствии чего частицы получают постоянно меняющийся импульс движения.

скорость диффузии прямо пропорциональна площади поверхности,

через которую проходит в-во, и градиенту его к-ции:

коэффициент диффузии сферических частиц прямо пропорционален абсолютной температуре и обратно пропорционален радиусу частицы и вязкости среды:

Уравнение позволяет объяснить малую скорость фиффузии коллоидных частиц. размеры коллоидных частиц приблизительно в 100 раз больше р-ров атомов, молекул и ионов НМВ. эксперементально определив коэффициент диффузии, с помощью уравнения можно вычислить р-ры диффундирующих частиц.

Осмотическое давление подчиняется з-ну Вант- Гоффа:

осматическое давление кол р-ра пропорционально числу частиц дисперсной фазы в единице объема и абсолютной температуре.

Из-за большого р-ра частиц и малых значений частичной концентрации осмотическое давление кол. р-ров в тысячу раз приблизительно ниже, чем у истинного р-ра такой же массовой доли.

Принимая, что коллоидная частица имеет шаровидную форму с радиусом r и считая, что плотность д. фазы равна р получают:

осматическое давление к. р-ра при прочих равных условиях обратно пропорционально кубу рудиуса к. частицы. зависимость эта позволяет объяснить, почему в отличии от истинных р-ров осм давление многих золей во времени падает. Это происходит в тех случаях, когда в р-те агрегации кол. частиц их размер возрастает, а частичная конц уменьшается. Кроме того ускоряется оседание частиц.

5. Оптические свойства коллоидных растворов. Уравнение Рэлля.

Для кол – дисп систем, 2r = Л падающего света. В этом случае преобладает дифракционное рассеяние света, когда каждая коллоидная частица становиться дополнительным источником света. визуально наблюдают опалесценцию. это явление заключается в том, что окраска кол. р-ров в рассеянном свете ( при рассмотрении сбоку) и в проходящем свете не одинакова

при рассмотрении сбоку хорошо виден опалесцирующий конус Фарадея-Тиндаля.

Инненсивность светорассеяния зависит от целого ряда факторов и количественно выражается у-нием Рэлеем:

интенсивность рассеянного света прямо пропорциональна интенсивности падающего света, частичной концентрации золя и шестей степени радиуса к. частицы и обратно пропорциональна четвертой степени длины падающей волны.

6. Методы изучения состава биополимеров. Электрофорез и электроосмос. Уравнение Гельмгольца-Смолуховского. Применение электрофоретических методов в медицине.

Электроосмос – перемещение частиц д фазы относительно неподвижной д. среды под д-вием внешнего эл. поля.

Положительно заряженные гранулы под д-вием эл. поля перемещаются к катоду, а отрицат противоионы диф слоя – к аноду. Качественно электрофорез равен электролизу. Различие количественное: под д-вием эл. поля в первом случае движутся частицы, а во втором – ионы, и на электродах выделяются сущ различные массы в-ва.

С помощью электрофореза можно определить знак зарядачастиц д. фазы и числовое значение электрокинетического потенциала.

Электроосмос – перемещение д. среды относительно неподвижной д. ф. по д-вие внешнего эл поля.

Скорость перемещения д. среды пасчитывается по у-нию:

Под д-вием внешнего эл. поля положительно заряженные противоины диф слоя вместе с гидратной оболочкой перемещаются к ктоду. В р-те происходит перемещение слоя жидкости к аноду

С помощью элосмоса можно определить числовое значение электрокинетического потенциала и знак заряда частиц д. фазы.

Использование в медицине.

эфорез используют в клинических исследованиях для диагностики многих заболеваний, для разделения аминокислот, нк к-т, антибиотиков, ферментов, антител, форменных эл. крови, бактериальных клеток, для определения частоты белковых препаратов

Источник

Броуновское движение и диффузия в коллоидных системах

Если частицы дисперсной фазы достаточно малы, как это имеет место в ультрамикрогетерогенных (коллоидных) системах, то обнаружи­вается их участие в тепловом движении. Оно проявляется в виде непрерывного самопроизвольного хаотического перемещения частиц, иначе называемого броуновским движением (по имени открывшего его в 1827 г. английского ботаника Р. Броуна (Брауна)). Броуновское движение наблюдается в системах с жидкой и газовой средой, где оно является причиной диффузии.

Движение частиц, названное его именем, Р. Браун обнаружил при рассматривании с помощью микроскопа спор папоротника и цветочной пыльцы, взвешенных в воде. Предположение о том, что причиной его является способность к движению живых объектов, вскоре пришлось оставить, так как мельчайшие частицы мрамора и других неживых материалов вели себя подобным же образом. Очень мелкие частицы при этом перемещаются на расстояния, во много раз превышающие их собственные размеры, более крупные частицы находятся в состоянии пос­тоянного колебания (дрожания) около положения равновесия. Дрожание и перемещение частиц ускоряется с повышением температуры и не связано с какими-либо внешними механическими воздействиями. Долгое время природа броуновского движения оставалась непонятной, пока в 1904 г. М. Смолуховский не объяснил её на основе атомно-молекулярного учения.

Причиной броуновского движения является то, что молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она испытывает огромное число одновременных ударов со всех сторон. Если частица имеет по сравнению с молекулами боль­шие размеры, то число этих ударов так велико, что по законам статис­тики результирующий импульс оказывается равным нулю, и такая частица не будет двигаться, чему способствует также её значительная инертность. В случае малых частиц ультрамикрогетерогенных систем вероятность неравномерного распределения импульсов, получаемых с разных сторон, увеличивается. В результате в зависимости от размеров и конфигурации частица приобретает колебательное, вращательное или поступательное движение. Таким образом, броуновское движение явилось первым экспериментальным подтверждением существования молекул и справедливости атомно-молекулярного учения.

Броуновское движение является главной движущей силой перемещения коллоидных частиц при диффузии.

Количественной характеристикой броуновского движения принято счи­тать средний сдвиг Dх частицы за время t, т. е. наблюдаемую проекцию отрезка прямой, соединяющей начальную точку движения (при t = 0), с положением частицы в момент t, на горизонтальную плоскость (рис. 7.1).

Рис. 7.1. Средний сдвиг частицы при броуновском движении

,

где К – коэффициент пропорциональности, в соответствии с теорией Эйнштейна равный

(k – константа Больцмана). Отсюда получаем уравнение Эйнштейна – Смолуховскогодля величины среднего квадратичного сдвига

или для среднего сдвига

.

Физический смысл коэффициента диффузии можно выяснить из рассмотрения первого закона А. Фика (1855 г.) для диффузии, согласно которому

,

А. Эйнштейном было выведено уравнение для расчёта коэффициента D. Исходным положением при выводе явилось то, что движущей силой диффузии является градиент концентрации. При этом на одну частицу действует средняя сила

где N_A — число Авогадро, С – молярная концентрация диффундирующего вещества.

Поскольку движение частиц происходит в среде с вязкостью h, скорость их перемещения может быть выражена с использованием уравнения Стокса:

(В – коэффициент трения по Стоксу, r – радиус движущейся частицы).

Сопоставляя это выражение и уравнение 1-го закона Фика, получаем уравнение Эйнштейнадля коэффициента диффузии:

Уравнения Эйнштейна и Эйнштейна – Смолуховского получены на основании предположения о тепловой природе броуновского движения. Поэтому сами они не могут служить доказательством правильности такого предположения, но помогают подтвердить его экспериментально. Справедливость закона Эйнштейна – Смолуховского для лиозолей была подтверждена Т. Сведбергом (1909), который с помощью ультрамикроскопанепосредственно измерял средний сдвиг частиц коллоидного золота в зависимости от времени и вязкости среды. Несколько позднее Ж. Перрен (1910) использовал закон Эйнштейна – Смолуховского для первого экспериментального определения числа Авогадро при изучении броуновского движения коллоидных частиц гуммигута в воде. Полученное им значение находилось в хорошем соответствии с теоретически вычисленными другими методами значениями числа Авогадро.

.

Для разбавленных систем, когда коэффициент диффузии не зависит от концентрации, а, следовательно, и от направления координаты х, получаем другую запись этого уравнения, называемую иногда уравнением второго закона Фика:

Это уравнение учитывает изменение концентрации во времени, происходящее в результате диффузии.

Все законы и закономерности диффузии, полученные при изучении коллоидных растворов, в полной мере применимы и к диффузии в истинных растворах, как в молекулярных, так и в растворах электролитов. Используя уравнение Эйнштейна – Смолуховского по известной скорости диффузии можно вычислить коэффициенты диффузии веществ, в том числе и лекарственных, что существенно для изучения поведения лекарств в жидких средах организма. С другой стороны, зная коэффициент диффузии, можно оценить размеры молекул лекарственных веществ, что также очень важно при изучении возможности проникновения их через поры в биологических мембранах – стенках клеток, кровеносных сосудов и т. д.

7.2. Седиментация и седиментационная устойчивость

Направление седиментации определяется разностью плотностей вещества дисперсной фазы и дисперсионной среды. Если частицы дисперсной фазы более плотные, чем дисперсионная среда, то происходит оседание или прямая седиментация.Если же имеет место обратное соотношение плотностей, то происходит всплывание частиц или обратная седиментация.

7.3. Закономерности седиментации в гравитационном поле.

Седиментация наблюдается в свободнодисперсных микрогетерогенных системах, из которых наиболее широко распространены (в том числе и в фар­ма­­ции) такие, как суспензии, эмульсии, аэрозоли.

На каждую частицу в системе действуют сила тяжести и сила вязкого сопротивления среды. Сила тяжести в соответствии с законом Ньютона равна

или с учётом выталки­вающей силы Архимеда

,

Сила вязкого сопротивления среды определяется законом Стокса и равна

,

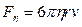
После некоторого начального промежутка времени, когда седиментирующая частица движется с ускорением, эти две силы уравновешивают друг друга и движение частицы становится равномерным. При этом

откуда получаем уравнение Стоксадля скорости седиментации:

7.4. Седиментация в центробежном поле

В высокодисперсных суспензиях скорость седиментацииочень мала. Кроме того, даже незначительные сотрясения и вибрация, а также неравномерность температуры приводят к тому, что уже осевшие частицы вновь поднимаются в объём суспензии. В коллоидных растворах броуновское движение и обусловленная им диффузия вообще препятствуют седиментации. Для того чтобы можно было проводить седиментационный анализ подобных систем, А. В. Думанским (1912 г.) было предложено использовать центробежное поле центрифуги. Однако обычные центрифуги со сравнительно малой частотой вращения не позволили получить заметного преимущества по сравнению с оседанием в гравитационном поле. Наблюдать и изучать седиментацию высокодисперсных систем удалось только после того, как Т. Сведберг сконструировал ультрацентрифугу, скорость вращения ротора которой достигает нескольких тысяч оборотов в секунду. Такая скорость позволяет получать ускорения до 10 5 – 10 6 g.

При оседании частицы её расстояние от центра вращения x увеличивается, из-за чего центробежная сила непрерывно возрастает, хотя угловая скорость остаётся постоянной. Чтобы учесть это изменение. следует выражение для силы трения, уравновешивающей центробежную силу, записать в виде

,

(Это выражение будет справедливо только в том случае, когда центробежная сила намного превышает силу тяжести, что обычно и имеет место при использовании ультрацентрифуги). При установившемся равновесии

и, значит, .

Разделяя переменные в этом уравнении и интегрируя его в пределах от х₀ до х и от t = 0 до t

,

или, так как ,

.

Константа седиментациив этом случае будет равна

.

7.5. Седиментационный анализ

При седиментационном анализе измеряется скорость накопления осадка во времени или другие пропорциональные ей величины. В гравитационном поле он проводится с помощью седиментометров различных конструкций. Ниже описано принципиальное устройство некоторых, наиболее употребительных из них.

Наиболее простой седиментометр представляет собой узкий стеклянный сосуд – цилиндр, пробирку или градуированную стеклянную трубку (например, микропипетку с закрытым для предотвращения выливания содержимого выходным отверстием). Скорость накопления осадка измеряется или по увеличению во времени высоты его слоя (как, например, при анализе СОЭ), или по увеличению свободной от частиц области суспензии в верхней части сосуда, т. е. по её осветлению. При исследовании эмульсий осветляться будет нижний, прилегающий ко дну слой жидкости. Такие седиментометры дают очень приблизительные результаты и к тому же они пригодны для исследования преимущественно монодисперсных систем.

Для более точных измерений используют и более сложные по конструкции седиментометры. Один из них, седиментометр Н. А. Фигуровского, представляет собой тонкую упругую стеклянную нить, одним концом закреплённую в штативе. К свободному концу на тончайшей нити или на волосе подвешивается лёгкая чашечка, изготовленная, например, из алюминиевой фольги.. Эта чашечка погружается в высокий цилиндр с исследуемой суспензией так, чтобы она находилась почти у дна. Частицы суспензии, оседая на чашечку, заставляют прогибаться стеклянную нить. Для измерения высоты прогиба нити служит вертикальная шкала, помещённая сзади неё. При достаточно упругой нити высота её прогиба прямо пропорциональна массе осевших на чашечку частиц. Измерения проводятся следующим образом. В хорошо перемешанную суспензию опускается чашечка седиментометра и в этот момент начинается отсчёт времени. Через определённые промежутки времени измеряется и записывается высота, на которую опустился свободный конец стеклянной нити. Измерения производятся до тех пор, пока не закончится оседание частиц, о чём можно заключить по получению трёх одинаковых отсчётов по шкале подряд.

Седиментометр С. Одена – это усовершенствованный вариант се­ди­мен­тометра Фигуровского. Вместо гибкой стеклянной нити чашечка в нём подвешивается к коромыслу торсионных весов, что позволяет контролировать во времени непосредственно массу оседающих частиц.

Седиментометр Вигнерапредставляет собой U-образную трубку, одно колено которой широкое, а другое – узкое, в виде градуированного капилляра. В широкое колено помещается исследуемая суспензия, а в узкий капилляр – чистая дисперсионная среда (вода в случае гидросуспензий). Накапливающийся на дне широкого колена осадок заставляет подниматься уровень жидкости в капилляре, высота которого и измеряется через определённые интервалы времени.

Решая уравнение Стоксаотносительно радиуса частицы, получим:

Отсюда следует, что, экспериментально измеряя скорость седиментации v и зная величины h, r и r₀, легко рассчитать радиус частицы.

Уравнение Стокса справедливо, если частицы дисперсной фазы осаждаются независимо друг от друга, что может быть только в раз­бавленных системах. При столкновениях частиц осаждение обычно за­медляется. Кроме того, оседание частиц в концентрированных системах заметно тормозится встречным потоком жидкости, поднимающейся со дна сосуда. Вносит искажения в седиментацию и неправильная форма частиц. В этом случае радиус, рассчитанный по уравнению Стокса, будет являться так называемым эквивалентным радиусом, равным радиусу сферичес­кой частицы, которая оседает с той же скоростью, что и данная реальная частица.

Зависимость скорости накопления осадка от времени, полученная с помощью седиментометра, изображается графически в виде седиментационной кривой.Анализ седиментационной кривой позволяет получать информацию о размерах частиц дисперсной фазы и о фракционном составе суспензии, эмульсии или порошка (который при смешивании с водой или другой жидкостью образует суспензию). Реальные суспензии полидисперсны и в них частицы с различными размерами оседают с различными скоростями. Седиментометр же регистрирует суммарную массу оседающих частиц всех размеров. Чтобы разобраться в принципе седиментационного анализа, предложенного С. Оденом, рассмотрим сначала седиментацию монодисперсной суспензии.

Она графически отображается в виде седиментационной кривой, показанной на рис. 7.2. Она представляет собой зависимость массы m накапливающегося осадка от времени t.

Рис. 7.2. Седиментационная кривая монодисперсной суспензии

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник