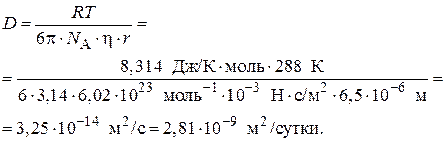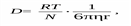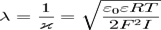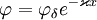Чем обусловлено броуновское движение частиц дисперсных систем
Броуновское движение
7 класс, без форм заявки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Молекулярно-кинетическая теория
Мы состоим из клеток, клетки состоят из молекул, молекулы из атомов, атомы из… Ладно, пока достаточно атомов. И молекулы, и атомы подчиняются законам, которые описаны в молекулярно-кинетической теории.
В основе молекулярно-кинетической теории лежат три основных положения:
Броуновское движение
Во второй половине ХIХ века в научных кругах разгорелась нешуточная дискуссия о природе атомов. На одной стороне дискуссии утверждали, что атомы — просто математические функции, удачно описывающие физические явления и не имеющие под собой реальной физической основы.С другой стороны настаивали, что атомы — это реально существующие физические объекты.
Самое смешное в этих спорах то, что за десять лет до их начала ботаник Роберт Броун уже провел эксперимент, который доказал физическое существование атомов. Вот, как это было:
Как Броун проводил эксперимент
Броун изучал поведение цветочной пыльцы под микроскопом и обнаружил, что отдельные споры совершают абсолютно хаотичные движения.
Представьте себе, что мы издалека наблюдаем, как плотная толпа людей толкает над собой большой мяч. Причём каждый толкает мяч, куда хочет. Мы не видим отдельных игроков, потому что поле далеко от нас, но мяч мы видим — и замечаем, что перемещается он очень беспорядочно.
Мяч постоянно меняет направление своего движения, и пойти в какую-нибудь определенную сторону не желает. Предсказать его местоположение через заданное время — нельзя.
Вот что-то похожее на это Броун увидел при изучении пыльцы.
В первую очередь он начал грешить на движение потоков воды или ее испарение, но проверив эту гипотезу, отмел ее. Проведя множество экспериментов, Броун установил, что такое хаотичное движение свойственно любым микроскопическим частицам — будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция. Но причины этого явления он выяснить не смог (не в обиду ботаникам, но все же, это не его специализация).
А теперь угадайте, кто смог применить этот эксперимент в доказательстве атомной теории строения вещества. Альберт Эйнштейн, кто же еще. Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды.
В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Однако, как бы ни мала была частица, в силу чисто случайных отклонений сначала она получает импульс со стороны молекулы, ударившей ее с одной стороны, а затем — со стороны молекулы, ударившей ее с другой. И так далее.
Чуть позже, через 3 года после открытия Эйнштейна, в 1908 году французский физик Жан Батист Перрен провел серию опытов, которые подтвердили правильность эйнштейновского объяснения броуновского движения. Стало окончательно ясно, что наблюдаемое «хаотичное» движение броуновских частиц происходит вследствие межмолекулярных соударений. Поскольку вывод о том, что несуществующие в природе математические функции не могут привести к физическому взаимодействию, напрашивается сам собой, стало окончательно ясно, что спор о реальности атомов окончен: они существуют в природе.
Также, если еще раз посмотреть на второе положение молекулярно-кинетической теории, можно заметить, что броуновское движение очень хорошо его доказывает: Атомы и молекулы находятся в непрерывном хаотическом движении.
Диффузия
Явление, которое доказывает первое и второе положения молекулярно-кинетической теории называется диффузия.
Диффузия в газах
Если в комнате открыть флакон с духами или зажечь ароматизированную свечу, то запах вскоре будет чувствоваться во всей комнате. Распространение запахов происходит из-за того, что молекулы духов проникают между молекулами воздуха. На самом деле, в этом процессе очень большую роль играет такой вид теплопередачи, как конвекция, но и без диффузии не обошлось.
На самом деле, молекулы вокруг нас движутся очень быстро — со скоростью в сотни метров в секунду — это напрямую зависит от температуры.
Давайте проверим это сами несложным экспериментом:
Замерьте температуру воздуха в помещении. Распылите освежитель воздуха в одном углу, встаньте в другой и включите секундомер. А лучше проведите эксперимент вдвоем, чтобы один человек распылял, а другой включал секундомер — так не будет погрешности, но будет веселье 😉
Как только почувствуете аромат освежителя в противоположном от места распыления, выключите секундомер. Запишите результат измерения. А потом проветрите помещение и проделайте все то же самое. Время, через которое до вас дойдет запах, будет другим. Во втором случае аромат будет распространяться медленнее.
То есть, чем выше температура, тем больше скорость диффузии.
Диффузия в жидкостях
Если диффузия в газах происходит быстро — чаще всего за считанные секунды — то диффузия в жидкостях занимает минуты или в некоторых случаях часы. Зачастую это зависит от температуры (как и в эксперименте выше) и плотности вещества.
С диффузией в жидкостях вы встречаетесь, когда, например, размешиваете краску. Или когда смешиваете любые две жидкости, например, газировку с сиропом. Также из-за диффузии происходит загрязнение рек (да и в целом окружающей среды).
Ну или вот пример диффузии в жидкостях, с которым вы точно не встречались — акулы ищут свою жертву по запаху крови, который распространяется в океане за счет диффузии.
Диффузия в твёрдых телах
Диффузия в твёрдых телах происходит очень медленно. Например, при комнатной температуре (около 20 °С) за 4-5 лет золото и свинец взаимно проникают друг в друга на расстояние около 1 мм.
Кстати, если вы проведете такой эксперимент, то увидите, что в свинец проникло малое количество золота, а свинец проник в золото на глубину не более одного миллиметра. Такое различие обусловлено тем, что плотность свинца намного выше плотности золота.
Этот процесс можно ускорить за счет нагревания, как в жидкостях и газах. Если на тонкий свинцовый цилиндр нанести очень тонкий слой золота, и поместить эту конструкцию в печь на неделю при температуре воздуха в печи 200 градусов Цельсия, то после разрезания цилиндра на тонкие диски, очень хорошо видно, что свинец проник в золото и наоборот.
Броуновское движение. Броуновское движение – беспорядочное движение частиц дисперсной фазы под действием тепловых ударов молекул дисперсионной среды



Броуновское движение – беспорядочное движение частиц дисперсной фазы под действием тепловых ударов молекул дисперсионной среды.
В результате огромного числа ударов со стороны молекул дисперсионной среды молекула дисперсной фазы меняет свое направление
и скорость весьма часто. Примерно за 1 с коллоидная частица может изменить свое направление свыше 10 20 раз.
Созданная Эйнштейном и Смолуховским в 1905–1906 гг. статистическая теория броуновского движения в качестве основного постулата исходит из предположения о совершенной хаотичности движения, т.е. полной равноправности всех направлений.
Для характеристики броуновского движения Эйнштейном и Смолуховским было введено понятие среднего квадратичного сдвига (броуновской площадки) 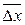
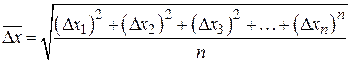
где 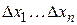
n – число проекций.
Величина среднего квадратичного сдвига связана с физическими характеристиками системы уравнением Эйнштейна – Смолуховского:
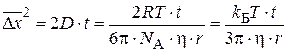
где t – время наблюдения.
Из уравнения следует, что частицы перемещаются тем быстрее, чем выше температура, меньше размер частиц r и вязкость среды η.
1. Вычислим коэффициент диффузии по уравнению Эйнштейна:
2. Вычислим проекцию среднего смещения частиц эмульсии:
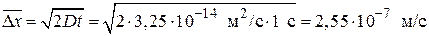
Молекулярно-кинетические свойства коллоидных растворов (диффузия, броуновское движение, осмос).



Молекулярно-кинетическискими называются с-ва, обусловленные хаотическим тепловым движением частиц.
Кол. р-ры частный случай истинных р-ров. Д. фаза – растворенное в-во, д. среда – растворитель.
Броуновское движение беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа. Броуновское движение никогда не прекращается.
Интенсивность броуновского движения зависит от р-ров частиц, температуры и вязкости жидкости.
Частицы дисперсной фазы испытывают в единицу времени огромное число ударов со стороны молекул дисперсионной среды, находящихся в тепловом движении. в следствии чего частицы получают постоянно меняющийся импульс движения.
скорость диффузии прямо пропорциональна площади поверхности,
через которую проходит в-во, и градиенту его к-ции:
коэффициент диффузии сферических частиц прямо пропорционален абсолютной температуре и обратно пропорционален радиусу частицы и вязкости среды:
Уравнение позволяет объяснить малую скорость фиффузии коллоидных частиц. размеры коллоидных частиц приблизительно в 100 раз больше р-ров атомов, молекул и ионов НМВ. эксперементально определив коэффициент диффузии, с помощью уравнения можно вычислить р-ры диффундирующих частиц.
Осмотическое давление подчиняется з-ну Вант- Гоффа:
осматическое давление кол р-ра пропорционально числу частиц дисперсной фазы в единице объема и абсолютной температуре.
Из-за большого р-ра частиц и малых значений частичной концентрации осмотическое давление кол. р-ров в тысячу раз приблизительно ниже, чем у истинного р-ра такой же массовой доли.
Принимая, что коллоидная частица имеет шаровидную форму с радиусом r и считая, что плотность д. фазы равна р получают:
осматическое давление к. р-ра при прочих равных условиях обратно пропорционально кубу рудиуса к. частицы. зависимость эта позволяет объяснить, почему в отличии от истинных р-ров осм давление многих золей во времени падает. Это происходит в тех случаях, когда в р-те агрегации кол. частиц их размер возрастает, а частичная конц уменьшается. Кроме того ускоряется оседание частиц.
5. Оптические свойства коллоидных растворов. Уравнение Рэлля.
Для кол – дисп систем, 2r = Л падающего света. В этом случае преобладает дифракционное рассеяние света, когда каждая коллоидная частица становиться дополнительным источником света. визуально наблюдают опалесценцию. это явление заключается в том, что окраска кол. р-ров в рассеянном свете ( при рассмотрении сбоку) и в проходящем свете не одинакова
при рассмотрении сбоку хорошо виден опалесцирующий конус Фарадея-Тиндаля.
Инненсивность светорассеяния зависит от целого ряда факторов и количественно выражается у-нием Рэлеем:
интенсивность рассеянного света прямо пропорциональна интенсивности падающего света, частичной концентрации золя и шестей степени радиуса к. частицы и обратно пропорциональна четвертой степени длины падающей волны.
6. Методы изучения состава биополимеров. Электрофорез и электроосмос. Уравнение Гельмгольца-Смолуховского. Применение электрофоретических методов в медицине.
Электроосмос – перемещение частиц д фазы относительно неподвижной д. среды под д-вием внешнего эл. поля.
Положительно заряженные гранулы под д-вием эл. поля перемещаются к катоду, а отрицат противоионы диф слоя – к аноду. Качественно электрофорез равен электролизу. Различие количественное: под д-вием эл. поля в первом случае движутся частицы, а во втором – ионы, и на электродах выделяются сущ различные массы в-ва.
С помощью электрофореза можно определить знак зарядачастиц д. фазы и числовое значение электрокинетического потенциала.
Электроосмос – перемещение д. среды относительно неподвижной д. ф. по д-вие внешнего эл поля.
Скорость перемещения д. среды пасчитывается по у-нию:
Под д-вием внешнего эл. поля положительно заряженные противоины диф слоя вместе с гидратной оболочкой перемещаются к ктоду. В р-те происходит перемещение слоя жидкости к аноду
С помощью элосмоса можно определить числовое значение электрокинетического потенциала и знак заряда частиц д. фазы.
Использование в медицине.
эфорез используют в клинических исследованиях для диагностики многих заболеваний, для разделения аминокислот, нк к-т, антибиотиков, ферментов, антител, форменных эл. крови, бактериальных клеток, для определения частоты белковых препаратов
Молекулярно-кинетические свойства коллоидных систем: броуновское движение, диффузия, осмотическое давление.
К молекулярно-кинетическим свойствам свободнодисперсных систем относятся: броуновское движение, диффузия, осмотическое давление, седиментация.
Броуновское движение проявляется хаотическим непрерывным движением частиц дисперсной фазы под действием ударов молекул растворителя (дисперсионной среды), находящихся в состоянии интенсивного молекулярно-теплового движения. Перемещаться частицы могут в различных направлениях. Траектория их движения представляет собой ломаную линию неопределенной конфигурации (рис.31).

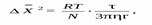
где ΔX – среднее смещение частицы, м –1 ; R – газовая постоянная, равная 8,31 Дж×моль/К; Т – температура, К; N – число Авогадро, моль –1 ; τ – время смещения, с; η – вязкость дисперсионной среды, Н×c/м 2 ; r – радиус дисперсной частицы, м.Из этого уравнения следует, что броуновское движение тем интенсивнее, чем меньше размер частиц и вязкость среды и чем выше температура. Броуновское движение не прекращается со временем, т.е. не зависит от длительности существования системы.
Диффузия – это самопроизвольно протекающий процесс выравнивания концентраций ионов, молекул или коллоидных частиц вследствие их беспорядочного теплового (для истинных растворов) или броуновского (для дисперсных систем) движения. Диффузия заканчивается с достижением равномерного распределения частиц по всему объему. Следовательно, диффузия возможна лишь в системах с неодинаковыми концентрациями.Величина, показывающая количество вещества, диффундирующего через поперечное сечение площадью 1 м 2 за 1 секунду при градиенте концентраций равном 1, называется коэффициентом диффузии.По формуле Стокса–Эйнштейна коэффициент диффузии связан с размерами диффундирующих частиц уравнением:
где D – коэффициент диффузии, м 2 /с.
Из этого уравнения следует, что чем больше размер частиц и выше вязкость среды, тем меньше скорость диффузии. Следовательно, при одинаковой температуре скорость диффузии в коллоидных растворах в сотни и тысячи раз меньше, чем в истинных растворах.
Осмотическое давление –одно из коллигативных свойств растворов, т.е. зависит только от количества свободно движущихся частиц. Следовательно, оно характерно, как для коллоидных растворов, так и для истинных, и для расчета величины осмотического давления коллоидных растворов также можно применить уравнение Вант-Гоффа:
Росм. = 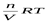
где Росм. – осмотическое давление золя, Па; n – количество частиц, моль; V– объем золя, м 3 ; R– газовая постоянная; Т– температура, К.
Если учесть, что объем и масса коллоидной частицы значительно больше, чем объем и масса молекулы низкомолекулярных веществ, то при одной и той же массовой концентрации вещества, в единице объема золя содержится значительно меньше частиц, чем в единице объема истинного раствора. Поэтому осмотическое давление коллоидных растворов ничтожно мало по сравнению с таковым в истинных растворах. Например, осмотическое давление золя золота с массовой концентрацией вещества 10 г/л равно 45 Па, а раствора сахарозы той же концентрации и в тех же условиях – 72500 Па.
Второй особенностью осмотического давления коллоидных растворов является его непостоянство. В связи с термодинамической неустойчивостью коллоидных растворов в них непрерывно протекают процессы агрегации и дезагрегации, приводящие к изменению числа осмотически активных частиц в единице объема, а, следовательно, и осмотического давления.
75.Классификация коллоидных систем. Механизм возникновения электрического заряда коллоидной частицы. Строение двойного электрического слоя. Мицелла. Ядро. Гранула.
Двойной электрический слой (межфазный) (ДЭС) — слой ионов, образующийся на поверхности частиц в результате адсорбции ионов из раствора, диссоциации поверхностного соединения или ориентирования полярных молекул на границе фаз. Ионы, непосредственно связанные с поверхностью называются потенциалоопределяющими. Заряд этого слоя компенсируется зарядом второго слоя ионов, называемых противоионами.
В отсутствие теплового движения частиц, строение двойного электрического слоя подобно строению плоского конденсатора. Но в отличие от идеального случая, ДЭС в реальных условиях имеет диффузное (размытое) строение. Согласно современной теории структуру ДЭС составляют два слоя:Слой Гельмгольца или адсорбционный слой, примыкающий непосредственно к межфазной поверхности. Этот слой имеет толщину δ, равную радиусу потенциалопределяющих ионов внесольватированном состояниДиффузный слой или слой Гуи, в котором находятся противоионы. Диффузный слой имеет толщину λ, которая зависит от свойств системы и может достигать больших значений. Толщина диффузного слоя рассчитывается по формуле:
Электрической характеристикой ДЭС является потенциал φ. Существует несколько характеристических потенциалов:Потенциал диффузного слоя φδ, соответствующий границе адсорбционного и диффузного слоёв. Внутри диффузного слоя потенциал можно рассчитать по уравнению Гуи-Чепмена:
· Потенциал φx=λ, меньший, чем φδ в e раз и характеризующий толщину диффузного слоя.Электрокинетический потенциал или дзета-потенциал. Этот потенциал соответствует плоскости скольжения и является частью потенциала диффузного слоя. Плоскость скольжения образуется в результате того, что при движении дисперсных частиц наиболее удаленная часть диффузного слоя не участвует в движении, а остается неподвижной. Поэтому появляется нескомпенсированность поверхностного заряда частицы и становятся возможными электрокинетические явления. Дзета-потенциал является одной из важнейших характеристик двойного электрического слоя.
Дата добавления: 2016-01-16 ; просмотров: 3894 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Броуновское движение
Нам известно, что все вещества состоят из огромного числа очень и очень маленьких частиц, которые находятся в непрерывном и беспорядочном движении. Откуда нам это стало известно? Как учёные смогли узнать о существовании настолько маленьких частиц, которые ни в один оптический микроскоп невозможно увидеть? И уж тем более, как им удалось выяснить, что эти частицы находятся в непрерывном и беспорядочном движении? В этом учёным помогли разобраться два явления — броуновское движение и диффузия. Об этих явлениях мы и поговорим более подробно.
2. Броуновское движение
Английский учёный Роберт Броун не был физиком или химиком. Он был ботаником. И он совсем не ожидал, что откроет столь важное для физиков и химиков явление. И он не мог даже подозревать о том, что в своих довольно простых экспериментах он будет наблюдать результат хаотичного движения молекул. А это было именно так.
Что же это были за эксперименты? Они были почти такие же, что делают ученики на уроках биологии, когда с помощью микроскопа пытаются рассмотреть, например, клетки растений. Роберт Броун хотел рассмотреть в микроскоп пыльцу растений. Рассматривая зёрна пыльцы в капле воды, он заметил, что зёрна не находятся в покое, а непрерывно дёргаются, будто они живые. Наверное, сначала он так и подумал, но будучи учёным, конечно же отбросил эту мысль. Ему не удалось понять, почему эти зёрна пыльцы ведут себя таким странным образом, но он описал всё увиденное, и это описание попало в руки физиков, которые тут же поняли, что перед ними наглядное доказательство непрерывного и беспорядочного движения частиц.
Объясняется это движение, описанное Броуном, следующим образом: зёрна пыльцы достаточно велики, так что мы можем увидеть их в обычный микроскоп, а вот молекулы воды мы не видим, но, в то же время, зёрна пыльцы достаточно малы, чтобы из-за ударов по ним молекул воды, окружающих их со всех сторон, они смещались то в одну, то в другую сторону. То есть этот хаотичный «танец» зёрен пыльцы в капле воды показывал, что молекулы воды непрерывно и беспорядочно с разных сторон ударяют по зёрнам пыльцы и смещают их. С тех пор непрерывное и хаотичное движение мелких твёрдых частичек в жидкости или газе стали называть броуновским движением. Важнейшей особенностью этого движения является то, что оно непрерывное, то есть не прекращается никогда.
Диффузия — это ещё один пример наглядного доказательства непрерывного и беспорядочного движения молекул. И заключается оно в том, что газообразные вещества, жидкости и даже твёрдые вещества, хотя и намного медленнее, могут самоперемешиваться друг с другом. К примеру, запахи различных веществ распространяются в воздухе даже в отсутствие ветра именно благодаря этому самоперемешиванию. Или вот ещё пример — если в стакан с водой бросить несколько кристаллов марганцовки и, не перемешивая воду, подождать около суток, то мы увидим, что вся вода в стакане будет окрашена равномерно. Это происходит из-за непрерывного движения молекул, которые меняются местами, и вещества постепенно перемешиваются самостоятельно без внешнего воздействия.
4. Свойства броуновского движения и диффузии
Когда учёные-физики стали более подробно рассматривать явление, описанное Робертом Броуном, они заметили, что, как и диффузию, этот процесс можно ускорить, повышая температуру. То есть в горячей воде и окрашивание с помощью марганцовки будет происходить быстрее, и движение мелких твёрдых частичек, к примеру, графитовой крошки или тех же зёрен пыльцы, происходит с большей интенсивностью. Это подтверждало тот факт, что скорость хаотичного движения молекул напрямую зависит от температуры. Не вдаваясь в подробности, перечислим, от чего может зависеть и интенсивность броуновского движения, и скорость протекания диффузии:
2) от рода вещества, в котором эти процессы происходят;
3) от агрегатного состояния.
То есть при равной температуре диффузия газообразных веществ протекает значительно быстрее, чем жидкостей, не говоря уже о диффузии твёрдых тел, которая происходит настолько медленно, что её результат, и то очень незначительный, можно заметить или при очень высоких температурах, или за очень большое время — годы или даже десятилетия.
5. Практическое применение
Диффузия и без практического применения имеет огромное значение не только для человека, но и для всего живого на Земле: именно благодаря диффузии в нашу кровь через лёгкие попадает кислород, именно посредством диффузии растения добывают из почвы воду, поглощают углекислый газ из атмосферы и выделяют в ней кислород, а рыбы дышат в воде кислородом, который из атмосферы посредством диффузии попадает в воду.
Явление диффузии применяется и во многих областях техники, причём именно диффузии в твёрдых телах. К примеру, есть такой процесс — диффузионная сварка. В этом процессе детали очень сильно прижимаются друг к другу, нагреваются до 800 °C и посредством диффузии происходит их соединение друг с другом. Именно благодаря диффузии земная атмосфера, состоящая из большого количества различных газов, не разделяется на отдельные слои по составу, а везде примерно однородна — а ведь будь иначе, мы вряд ли смогли бы дышать.
Существует огромное количество примеров влияния диффузии на нашу жизнь и на всю природу, которые может найти любой из вас, если захочет. А вот о применении броуновского движения мало что можно сказать, кроме того, что сама теория, которая описывает это движение, может применяться и в других, казалось бы совершенно не связанных с физикой, явлениях. К примеру, эту теорию используют для описания случайных процессов, с применением большого количества данных и статистики — таких, как изменение цен. Теория броуновского движения используется для создания реалистичной компьютерной графики. Интересно, что человек, заблудившийся в лесу движется примерно так же, как и броуновские частички — блуждает из стороны в сторону, многократно пересекая свою траекторию.
6. Методические рекомендации учителям
1) Рассказывая классу о броуновском движении и диффузии, необходимо сделать акцент на том, что эти явления не доказывают факт существования молекул, но доказывают факт их движения и то, что оно беспорядочное — хаотичное.
2) Обязательно обратите особое внимание на то, что это непрерывное движение, зависящее от температуры, то есть тепловое движение, которое не может прекратиться никогда.
3) Продемонстрируйте диффузию с помощью воды и марганцовки, дав задание наиболее любознательным ребятам провести подобный эксперимент в домашних условиях и делая фотографии воды с марганцовкой через каждый час-два в течение дня (в выходной дети это с удовольствием сделают, а фото пришлют вам). Лучше, если в подобном эксперименте будет две ёмкости с водой — холодной и горячей, чтобы можно было продемонстрировать наглядно зависимость скорости диффузии от температуры.
4) Попробуйте измерить скорость диффузии в классе с помощью, к примеру, дезодоранта — в одном конце класса распыляем небольшое количество аэрозоля, а в 3-5 метрах от этого места ученик с секундомером фиксирует время, через которое он почувствует запах. Это и весело, и интересно, и запомнится детьми надолго!
5) Обсудите с детьми понятие хаотичности и тот факт, что даже в хаотических процессах учёные находят некие закономерности.