Чем обусловлена свободная конвекция
Конвекция
Содержание
Теплопередача бывает трех видов: теплопроводность, конвекция и излучение. В прошлом уроке вы познакомились с теплопроводностью. При этом явлении внутренняя энергия передается от одной части тела к другой или от одного тела к другому. Это тесно связано со структурой рассматриваемого вещества и тепловым движением частиц в нем.
Когда мы будем говорить о конвекции, речь будет идти не о движении отдельных частиц, а о движении групп частиц. В данном уроке мы выясним определяющую разницу явления конвекции от теплопроводности и дадим ему определение. Далее рассмотрим конвекцию в жидкостях и газах, узнаем это явление в бытовых примерах и природе.
Определение конвекции
Возьмем пробирку и наполним ее водой. Начнем нагревать верхнюю часть пробирки пламенем спиртовки (рисунок 1, а).
Вода на поверхности пробирки закипит, тогда как у ее дна она останется просто теплой. Этот пример определяется теплопроводностью воды. Она у жидкостей невелика.
А теперь проделаем такой же опыт, но с небольшим изменением. Переместим пламя спиртовки в нижнюю часть пробирки (рисунок 1, б).
На этот раз вода в пробирке по всему объему достаточно быстро нагреется и закипит. Значит, здесь перенос энергии осуществляется не за счет теплопроводности жидкости, а на основании другого явления – конвекции.
Конвекция (от лат. конвекцио – перенесение) – это вид теплопередачи, при котором энергия переносится струями газа или жидкости.
Конвекция в жидкостях
Когда мы нагреваем жидкость снизу, в первую очередь нагревается самый нижний слой воды. Он становится теплее остальной жидкости. При нагревании вода расширяется и ее плотность уменьшается. Такой слой воды становится более легким. В итоге, нагретые слои вытесняются вверх более тяжелыми холодными слоями.
Холодные слои, опустившись вниз, нагреваются от источника тепла. Далее они тоже вытесняются менее нагретой водой.
Благодаря такому постоянному движению, вода равномерно нагревается.
Такое движение слоев объясняется действием архимедовой силы. При увеличении объема нагретого слоя, увеличивается действующая на него архимедова сила. Она становится больше силы тяжести, действующей на данный слой. Он поднимается наверх.
Наглядно это можно пронаблюдать на опыте, изображенном на рисунке 3.
Здесь в жидкость добавляют марганцовку и начинают ее нагревать. Нагретая в пламени свечи вода начинает расширяться и поднимается наверх. Так как вода окрашена неравномерно, легко пронаблюдать циркуляцию.
Конвекция в газах
Если мы поместим руку над горячей плитой, то почувствуем, как над ней поднимаются теплые струи воздуха. Это происходит конвекция в воздухе.
Пронаблюдаем это явление на опыте (рисунок 4). У нас есть вертушка и свечи, расположенные под ней.
После того как мы зажжем все свечи, мы увидим, что вертушка начала вращаться. Что же здесь происходит?
Воздух, соприкасающийся с пламенем свечей, нагревается, расширяется и становится менее плотным. На него со стороны холодного воздуха действует сила Архимеда снизу вверх. Эта сила становится больше силы тяжести, действующей на теплый воздух. В итоге, теплый воздух начинает подниматься вверх, а его место занимает холодный воздух.
Если мы будем постепенно тушить свечи, то увидим, что скорость вращения вертушки начинает снижаться. Это связано с уменьшением объема циркулирующего воздуха.
Свойства и виды конвекции
Мы выясняли (рисунок 1, а), что если подогревать жидкость не снизу, то конвекция не будет происходить. То же самое справедливо и для конвекции в газах. Нагретые слои не смогут опуститься ниже холодных, более тяжелых. Значит,
для осуществления конвекции в жидкостях и газах необходимо нагревать их снизу.
Может ли происходить конвекция в твердых тела? В твердых телах частицы совершают колебания около определенных положений. Их удерживает сильное взаимное притяжение. В такой ситуации невозможно образование потоков вещества, как в жидкостях или газах. Следовательно,
конвекция не может происходить в твердых телах.
Конвекция бывает двух видов (рисунок 5):
Примерами естественной конвекции являются все примеры, которые мы рассмотрели выше.
Вынужденная конвекция наблюдается, например, если мы используем веер или перемешиваем жидкость ложкой.
Конвекция в быту и природе
Явление конвекции легко просматривается в наших квартирах. Когда в холодное время работает отопление, в комнатах постоянно происходит ощутимая циркуляция воздуха (рисунок 6).
Отметьте для себя тот факт, что в явлении конвекции кроется причина того, что отопительные батареи размещают в нижней части стен, ближе к полу.
Иногда в одной комнате бывает теплее, чем в соседней. Например, стоит дополнительная батарея или работает печка в кухне. В дверном проеме между такими комнатами можно обнаружить потоки воздуха (рисунок 7).
Холодный воздух будет иметь большую плотность и находится внизу. Если мы подставим пламя зажигалки внизу дверного проема, то увидим, что холодный воздух двигается в более теплую комнату. Если же поместим горящую зажигалку в верхнюю часть проема, то пламя отклонится в другую сторону. Так теплый воздух движется в холодную комнату.
Яркий пример конвекции в природе – это ветер. Наша атмосфера по всей Земле прогревается неодинаково. Из-за разного нагрева воздуха в жарких тропиках и полярных областях возникает мощное конвекционное движение воздуха – образуются ветра.
Пассаты – ветра, дующие от субтропических областей с экватору – частично образуются из-за неравномерного нагревания земной поверхности. Из-за вращения Земли, потоки воздуха отклоняются от меридиана (рисунок 8). Поэтому в Северном полушарии пассаты движутся в северо-восточном направлении, а в Южном – в юго-восточном направлении.
Ветра способствуют образования течений. Верхние слои воды (поверхностное течение) движутся в направлении постоянно дующего ветра (рисунок 9). Так, теплые и холодные течения – пример вынужденной конвекции.
Ветер на берегах морей – бриз – также образуется за счет конвекции (рисунок 10).
В теплое время года суша днем прогревается сильнее, чем море. Нагретые слои воздуха поднимаются вверх. Их давление становится меньше давления более холодного воздуха. Так, днем воздух дует с моря (дневной бриз), потому что прохладный воздух замещает собой теплый. Ночью все происходит наоборот – вода в море остывает медленнее, чем поверхность суши. Ветер дует с суши на море – образуется ночной бриз.
Естественная конвекция
СОДЕРЖАНИЕ
Принципы [ править ]
Примеры [ править ]
Гольфстрим циркулирует в результате испарения воды. В этом процессе вода становится соленой и плотной. В северной части Атлантического океана вода становится настолько плотной, что начинает опускаться вниз.
В ядерном реакторе естественная циркуляция может быть критерием проектирования. Это достигается за счет уменьшения турбулентности и трения в потоке жидкости (то есть минимизации потерь напора ) и предоставления способа удаления любых неработающих насосов из тракта жидкости. Кроме того, реактор (как источник тепла) должен быть физически ниже, чем парогенераторы или турбины (радиатор). Таким образом, естественная циркуляция будет гарантировать, что текучая среда будет продолжать течь, пока реактор будет горячее, чем теплоотвод, даже когда мощность не может быть подана на насосы.
По природе естественной циркуляции жидкости обычно движутся не очень быстро, но это не обязательно плохо, поскольку высокие скорости потока не являются существенными для безопасной и эффективной работы реактора. В современных ядерных реакторах реверс потока практически невозможен. Все ядерные реакторы, даже те, которые предназначены в первую очередь для использования естественной циркуляции в качестве основного метода циркуляции жидкости, имеют насосы, которые могут циркулировать жидкость в случае, если естественной циркуляции недостаточно.
Параметры [ править ]
Начало [ править ]
Возникновение естественной конвекции определяется числом Рэлея ( Ra ). Это безразмерное число дается выражением
Ра знак равно Δ ρ грамм L 3 D μ <\ displaystyle <\ textbf
Естественная конвекция будет более вероятной и / или более быстрой с большим разбросом плотности между двумя жидкостями, большим ускорением силы тяжести, которое вызывает конвекцию, и / или большим расстоянием через конвектирующую среду. Конвекция будет менее вероятной и / или менее быстрой при более быстрой диффузии (тем самым рассеивая градиент, вызывающий конвекцию) и / или более вязкой (липкой) жидкости.
Для тепловой конвекции из-за нагрева снизу, как описано выше в котле для кипячения, уравнение модифицировано с учетом теплового расширения и температуропроводности. Изменения плотности из-за теплового расширения выражаются следующим образом:
Вставка этих замен дает число Рэлея, которое можно использовать для прогнозирования тепловой конвекции. [7]
Ра знак равно ρ 0 грамм β Δ Т L 3 α μ <\ displaystyle <\ textbf
Турбулентность [ править ]
Тенденция конкретной естественно конвективной системы к турбулентности зависит от числа Грасгофа (Gr). [8]
грамм р знак равно грамм β Δ Т L 3 ν 2 <\ displaystyle Gr = <\ frac
В очень липких, вязких жидкостях (большие ν ) движение жидкости ограничено, и естественная конвекция не будет турбулентной.
Поведение [ править ]
грамм р знак равно грамм β Δ C L 3 ν 2 <\ displaystyle Gr = <\ frac
Естественная конвекция сильно зависит от геометрии горячей поверхности, существуют различные корреляции для определения коэффициента теплопередачи. Общая корреляция, применимая к различным геометриям, такова:
N ты знак равно [ N ты 0 1 2 + р а 1 6 ( ж 4 ( п р ) 300 ) 1 6 ] 2 <\displaystyle Nu=\left[Nu_<0>^<\frac <1><2>>+Ra^<\frac <1><6>>\left(<\frac
Значение f 4 (Pr) рассчитывается по следующей формуле
f 4 ( P r ) = [ 1 + ( 0.5 P r ) 9 16 ] − 16 9 <\displaystyle f_<4>(Pr)=\left[1+\left(<\frac <0.5>
Естественная конвекция от вертикальной пластины [ править ]
В этой системе тепло передается от вертикальной пластины к жидкости, движущейся параллельно ей за счет естественной конвекции. Это будет происходить в любой системе, в которой плотность движущейся жидкости изменяется в зависимости от положения. Эти явления будут иметь значение только тогда, когда на движущуюся жидкость минимально влияет принудительная конвекция. [9]
Если считать, что поток жидкости является результатом нагрева, можно использовать следующие корреляции, предполагая, что жидкость является идеальной двухатомной, имеет прилегающую к вертикальной пластине при постоянной температуре и поток жидкости является полностью ламинарным. [10]
Nu m = 0,478 (Gr 0,25 ) [10]
Среднее число Нуссельта = Nu m = h m L / k [10]
Число Грасгофа = Gr = [9] [10] [ g L 3 ( t s − t ∞ ) ] / v 2 T <\displaystyle [gL^<3>(t_-t_<\infty >)]/v^<2>T>
Когда поток является турбулентным, необходимо использовать различные корреляции, включающие число Рэлея (функция как числа Грасгофа, так и числа Прандтля ). [10]
Формирование паттернов [ править ]
Конвекция воды при отрицательных температурах [ править ]
Мантийная конвекция [ править ]
Введение в моделирование свободной конвекции в COMSOL Multiphysics®
Свободная конвекция играет важную роль во многих научных и прикладных задачах, таких как охлаждение электронных компонентов, кондиционирование в помещений и перенос вещества в окружающей среде. Модули Вычислительная гидродинамика и Теплопередача в версии 5.2a программного пакета COMSOL Multiphysics® включают функциональные возможности, позволяющие проще формулировать и решать задачи свободной конвекции. В этой статье мы расскажем о свободной конвекции, о новых функциональных возможностях и о некоторых проблемах, с которыми вы можете столкнуться при ее моделировании.
Что такое свободная конвекция?
Свободная конвекция — вид переноса вещества, вызванный действием выталкивающей (архимедовой) силы. Архимедова сила, в свою очередь, создается за счет неоднородной плотности среды переменного состава или температуры.
Вы могли сталкиваться с явлением свободной конвекции в системах кондиционирования помещений. В этом случае теплый воздух вблизи источников тепла поднимается вверх к потолку, а холодный воздух вблизи холодных поверхностей (таких как окна в зимний период) опускается вниз к полу.
Другой пример процесса, ход которого зависит от свободной конвекции, — охлаждение электроники. Например, нежелательно использовать шумные вентиляторы для охлаждения усилителей и телевизоров в домашних кинотеатрах. Электронное оборудование, работающее в тихой обстановке, обычно охлаждают с помощью свободной конвекции воздуха, обдувающего встроенные радиаторы.
Свободная конвекция вокруг расходящегося игольчатого радиатора, нагреваемого снизу Анимация показывает величину скорости потока воздуха вокруг радиатора.
В химической и пищевой промышленности существуют менее очевидные задачи, связанные со свободной конвекцией. Экологи и метеорологи тоже сталкиваются с задачей свободной конвекции, когда пытаются предсказать и понять явления переноса в воздухе и в воде.
Во всех упомянутых случаях инженерам и ученым важно понимать свойства свободной конвекции и проектировать системы, позволяющие применять эти свойства. Математическое моделирование здесь незаменимо. В последней версии COMSOL Multiphysics определять и решать задачи, связанные со свободной конвекцией, стало еще проще. Для этого мы добавили ряд новых возможностей.
Вариант Weakly compressible flow (Слабосжимаемый поток) для гидродинамических интерфейсов не учитывает влияние волн давления, которые редко играют роль в процессах свободной конвекции. Это позволяет увеличить шаг по времени и сократить время вычисления для задач свободной конвекции.
Вариант Incompressible flow (Несжимаемый поток) и приближение Буссинеска для потока, создаваемого архимедовой силой, линеаризуют плотность при помощи коэффициента термического расширения. Этот вариант учитывает изменение плотности в уравнении сохранения импульса только в слагаемом для объемной силы. Это еще более грубое упрощение по сравнению с вариантом Weakly compressible flow (Слабосжимаемый поток), но оно по-прежнему дает эффективное и точное описание систем с малыми вариациями плотности. Это упрощение почти всегда верно для свободной конвекции в воде при малых разностях температур.
Функциональная возможность Gravity (Сила тяжести) позволяет легко задавать точку отсчета гидростатического давления и автоматически учитывает изменения гидростатического давления на вертикальных границах.
Давайте подробнее изучим эти новые возможности и научимся применять их к задачам моделирования свободной конвекции.
Как решать задачи свободной конвекции с помощью модели слабосжимаемой среды
Интерфейс Nonisothermal Flow (Неизотермический поток) предоставляет опцию Weakly Compressible Flow (Слабосжимаемый поток), которая упрощает решение задач конвекции, не учитывая изменения плотности из-за давления. Этот вариант также не учитывает волны давления, расчет которых требует плотную сетку и маленький временной шаг, а значит занимает много времени. Волны давления редко влияют на свободную конвекцию, поэтому мы мало потеряем в точности модели, применив такое упрощение.
Уравнение непрерывности для сжимаемой жидкости имеет вид
где ρ — плотность, а u — вектор скорости.
Для газа плотность пропорциональна давлению и температуре. Например, для идеального газа
Если пренебречь динамическими эффектами изменения плотности, получим
Используя выражение для плотности идеального газа и пренебрегая зависимостью плотности от давления, получаем уравнение неразрывности
Это означает, что изменение плотности обусловлено только изменением температуры. Изменение плотности может вызвать расширение текучей среды, но прямое динамическое влияние этого расширения на поле давления с настройками Weakly compressible flow (Слабосжимаемый поток) не учитывается.
Кроме выражения для плотности в уравнении неразрывности, можно добавить объемную силу, сонаправленную силе тяжести, к уравнению сохранения импульса, выбрав флажок Gravity (Сила тяжести) в настройках интерфейса потока среды. По умолчанию она направлена в отрицательном направлении оси z. Эта сила имеет вид
где плотность ρ зависит от температуры.
Для идеального газа плотность обратно пропорциональна температуре.
Вы можете найти настройки для варианта Weakly compressible flow (Слабосжимаемый поток), выбрав интерфейс Nonisothermal Flow (Неизотермический поток) или интерфейс Conjugate Heat Transfer (Сопряженная теплопередача). Выберите в Построителе моделей интерфейс Fluid Flow (Поток текучей среды), чтобы увидеть окно настроек, как на рисунке ниже. Выбрав вариант Weakly compressible flow (Слабосжимаемый поток), вы устраните зависимость между давлением и плотностью, а включив флажок Gravity (Сила тяжести) — автоматически добавите объемную силу к уравнению импульса.
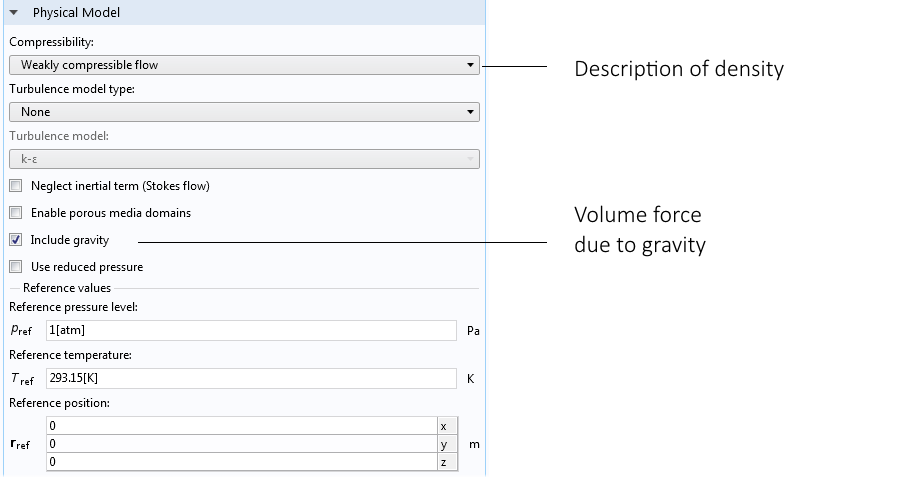
Окно настроек интерфейса Fluid Flow (Поток текучей среды), показывающее опции Weakly compressible flow (Слабосжимаемый поток) и Gravity (Сила тяжести).
На графике ниже показан поток между двумя вертикальными печатными платами. На рисунке показана только элементарная ячейка одной печатной платы. Вторая печатная плата размещена непосредственно перед ней, задней стороной к той плате, которую мы видим. Поток полностью обусловлен архимедовой силой, вентилятора нет.
Скорость потока на входе составляет примерно 0,2 м/с, а на выходе — примерно 0,3 м/с. Воздух не поступает с боковых сторон, а значит, разность скоростей потока обусловлена расширением воздуха из-за повышения температуры воздуха в канале между двумя печатными платами.
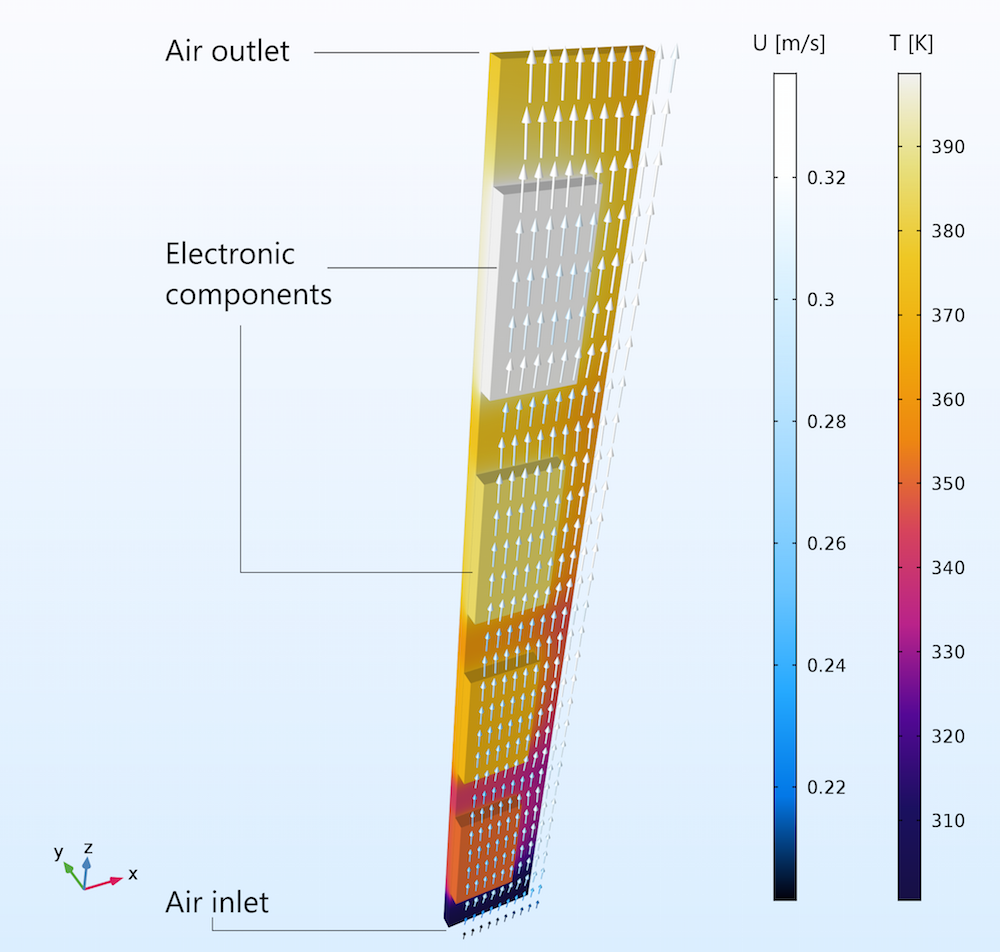
Созданный архимедовой силой поток между двумя вертикальными печатными платами. Расширение показано с помощью цветовой схемы стрелок: скорость потока на входе примерно 0,2 м/с, а на выходе — примерно 0,3 м/с.
Несжимаемая среда с приближением Буссинеска
Если изменения плотности и связанное с ними расширение пренебрежимо мало влияют на поле скорости потока, мы можем использовать опцию Incompressible flow (Несжимаемый поток) и приближение Буссинеска для свободной конвекции. Тогда уравнение неразрывности еще больше упрощается, чем в случае опции Weakly compressible flow (Слабосжимаемый поток), потому что текучая среда теперь считается несжимаемой. Уравнение неразрывности принимает вид
Вместо этого малые изменения плотности учитываются посредством объемной силы, которую добавляют в уравнение сохранения импульса и которая направлена противоположно силе тяжести, то есть, по умолчанию, в направлении оси z. Малые изменения плотности вычисляют, линеаризуя температурную зависимость плотности среды. Z-компонента объемной силы становится равна
где g — постоянная силы тяжести, \[<\rho _<<\text>>>\] — плотность при исходной температуре, α — коэффициент термического расширения среды, ΔT — разность температур.
Преимущество приближения Буссинеска для потоков, создаваемых архимедовой силой, заключается в уменьшении нелинейной составляющей уравнений гидродинамики — такую задачу проще решить численно, она требует меньше итераций и позволяет использовать большие шаги по времени в нестационарных задачах.
Например, приближение Буссинеска дает близкое к реальности описание потока воды при относительно малых разностях температуры. На рисунке ниже показана свободная конвекция в стакане воды, который нагревают снизу. Мы наблюдаем очень сложную картину потоков: потоки в центре и у дна стакана направлены вверх, а потоки между стенками и центром стакана направлены вниз.
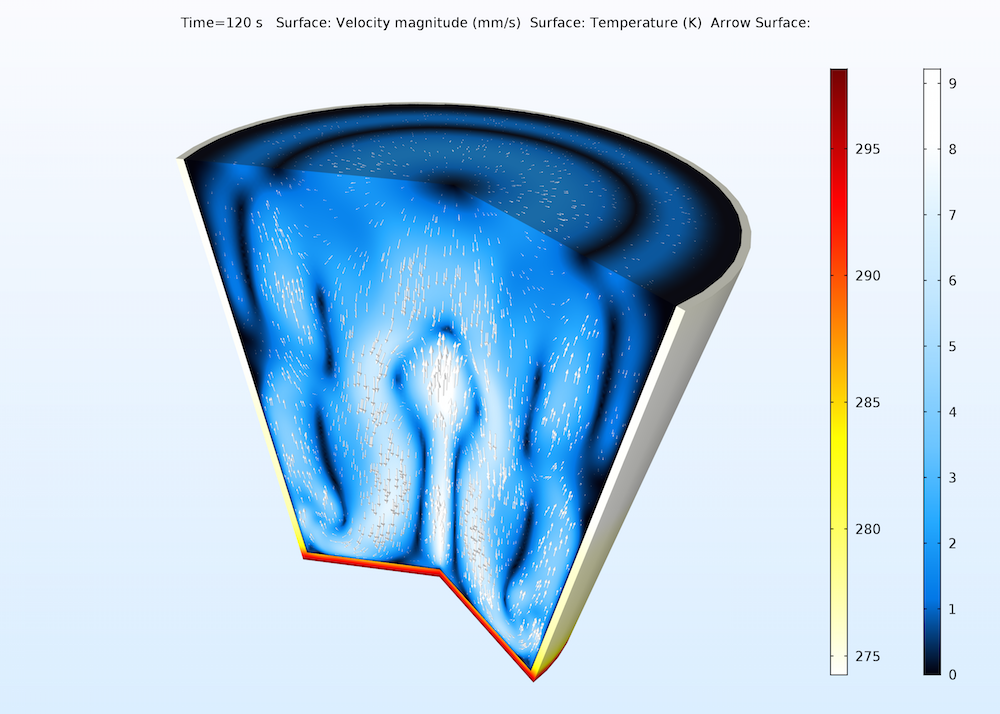
Свободная конвекция в стакане воды. График показывает поле скорости потока в стакане и распределение температуры на стенках стакана.
Мы можем использовать вариант Incompressible flow (Несжимаемый поток) вместе с приближением Буссинеска для потока, обусловленного архимедовой силой, выбрав настройки для гидродинамических интерфейсов в COMSOL Multiphysics, показанные на рисунке ниже.
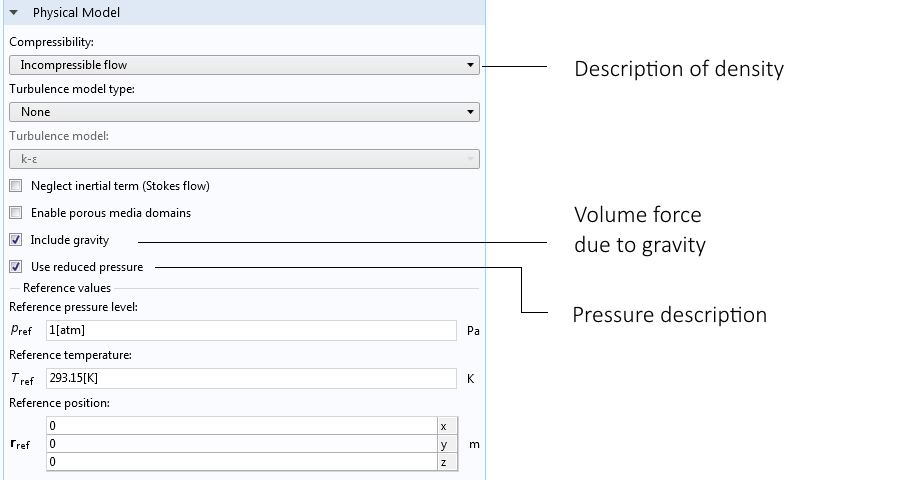
Опции Incompressible flow (Несжимаемый поток), Gravity (Сила тяжести) и упрощенное задание давления позволяют использовать приближение Буссинеска для задачи свободной конвекции.
Задание уравнения для давления в моделях свободной конвекции
При моделировании сжимаемого потока зависимость давления от времени включена в уравнение непрерывности, поскольку для сжимаемых текучих сред плотность является функцией давления. Это означает, что для хорошей постановки задачи обычно достаточно задать начальное условие по давлению, даже если мы не задаем давление на границе.
Для слабосжимаемых и несжимаемых потоков, как мы обсуждали выше, зависимость давления от времени в уравнении непрерывности опускается. Если граничные условия не задают давление, то поле давления не может быть однозначно определено до тех пор, пока мы не зададим давление хотя бы в одной точке области.
В COMSOL Multiphysics мы можем задать так называемое ограничение давления в точке, чтобы избежать неопределенности при расчете поля давления. Отсутствие условия для точки отсчета давления часто приводит к проблемам со сходимостью в задачах свободной конвекции.
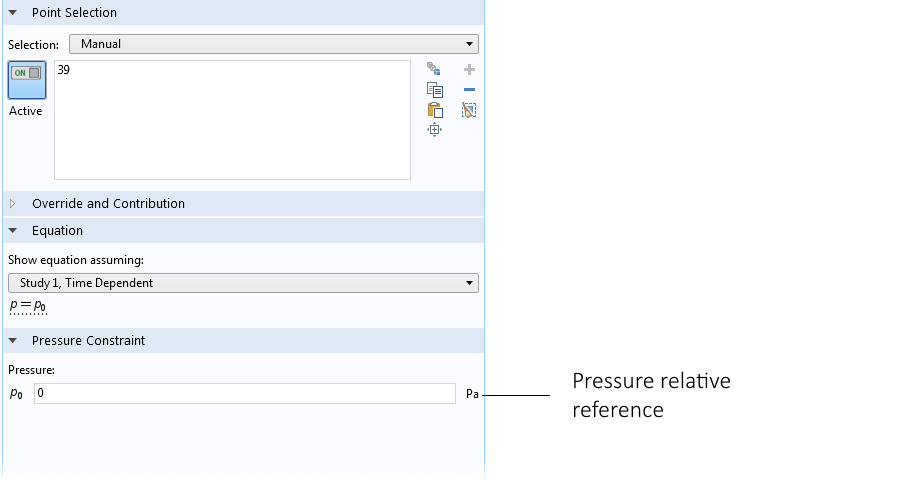
Настройки для ограничения давления в точке на примере со стаканом воды.
Использование связывания и разделения переменных для задач свободной конвекции
Уравнения, описывающие свободную конвекцию, обычно включают уравнение сохранения импульса, уравнение неразрывности и уравнение переноса энергии или массообмена. Если выталкивающая сила создается разностью температур, то уравнение энергетического обмена жестко связано с уравнениями гидродинамики (уравнения Навье–Стокса). В случае свободной конвекции эта взаимосвязь очень тесна. Таким образом, самый надежный способ решить эти уравнения — использовать полностью связный решатель в COMSOL Multiphysics.
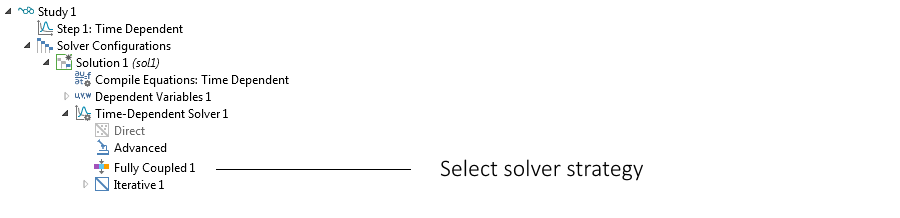
Узел Solver (Решатель) в дереве модели и настройки полностью связного решателя.
Для очень больших задач предпочтительным может оказаться раздельный подход. Например, если в задаче есть несколько химических веществ и выталкивающая сила создается за счет разного химического состава, то решатель с разделением переменных может оказаться единственным вариантом, не требующим чрезмерного объема памяти.
Заключение
Я хотел бы закончить эту статью еще одним примером, связанным со свободной конвекцией. Я часто думаю о свободной конвекции, куря сигару. Хотя я и не хочу рекламировать сигары, мой любимый пример свободной конвекции — сигарный дым, поднимающийся в холодный зимний воздух. На рисунке ниже показана зажженная сигара на пепельнице и распределение скорости в потоке, вызванном теплом сгорания.
Свободная конвекция (с небольшой составляющей вынужденной конвекции) воздуха вокруг зажженной сигары на пепельнице.

