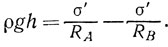Чем обусловлена шарообразная форма капель
Проект по теме: Физическая лаборатория «Капля жидкости»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Муниципальное автономное общеобразовательное учреждение
Средняя образовательная школа №2
Шуплецова Вера Николаевна
Перевалова Наталья Васильевна
Практическая часть…………. 7
Этапы реализации проекта …………………………………………14
В процессе выполнения работы: проведения наблюдений и опытов с каплями жидкости, создаётся обучающий комплекс под названием: Физическая лаборатория: «Капля жидкости», то есть набор приборов и материалов, которые можно использовать на факультативных занятиях и уроках физики.
Не сложные и интересные опыты можно выполнить, используя доступные и не дорогие материалы.
Получение новых знаний в результате эксперимента с каплями жидкости
3)Разработать инструкции для лабораторных работ
4)Создать электронное пособие: «Капля жидкости»
Обучающий комплекс – физическая лаборатория: «Капля жидкости» состоит из:
Прибор для создания капель жидкости
Набор для изучения явления смачивания и не смачивания
Наглядное пособие «Опыт Плато»
Разработки лабораторных работ
Электронное наглядное пособие
Целевые группы проекта
Ученики 7-10 классов
Планируемые результаты проекта
Применение проекта на факультативе в 7 «Н» классе
Место и время реализации проекта
20 февраля 2016 год
«Капля — это кусочек мира, в котором мы живём и который мы стремимся узнать» (Я. Гегузин)
Капля — небольшой объём жидкости, ограниченный поверхностью, определяемой преимущественно действием сил поверхностного натяжения, а не внешних сил.
Капля – маленькая частица какой-либо жидкости, принявшая округлую форму.
Капля – минимальное кол-во жидкости, принимающее округленную форму в следствие сцепления её частиц.
Форма капли определяется действием поверхностного натяжения и внешних сил (в первую очередь силы тяжести). Микроскопические капли, для которых сила тяжести не играет определяющей роли, имеют форму шара — тела с минимальной для данного объёма поверхностью (так как молекулы воды равномерно притягиваются друг другу). Крупные капли в атмосфере имеют шарообразную форму только при равенстве плотностей жидкости капли и окружающей её среды.
Падающие дождевые капли под действием силы тяжести, давления встречного потока воздуха и поверхностного натяжения принимают вытянутую форму.
При соприкосновении жидкости с твердым телом наблюдается явление смачивания или несмачивания.
Явление смачивания и не смачивания.
Эти явления являются проявлением сил поверхностного натяжения. В обычных земных условиях на смачиваемых поверхностях капли обычно растекаются, потому что если жидкость смачивает твердое тело, то это значит, что молекулы жидкости притягиваются сильные друг к другу, чем к молекулам твердого тела, а на не смачиваемых принимают форму сплюснутых шаров, потому что, когда наблюдается несмачиваемость, то это означает, что молекулы жидкости притягивается сильнее друг к другу, чем к молекулам твердого тела.
Явление смачивания применяют при обогащении руд. Суть обогащения состоит в отделении пустой породы от полезных ископаемых. Этот способ носит название флотации (флотация – всплывание). Раздробленную в мелкий порошок руду взбалтывают в воде, в которую добавлено небольшое количество жидкости, смачивающей полезную руду, например масло. Вдувая в эту смесь воздух, можно отделить обе составляющие. Покрытые пленкой кусочки полезной руды, прилипая к пузырькам воздуха, поднимутся вверх, а порода осядет на дно.
Благодаря явлению смачивания, мы можем рисовать красками, писать чернилами на бумаге,мыть посуду, стирать бельё. А благодаря явлению не смачивания, мы ходим в плащах, смело топаем по лужам, если обувь обработана водоотталкивающим средством.
Подтверждением действия сил поверхностного натяжения является опыт Плато.
Впервые опыт был выполнен в 1849 г. под руководством бельгийского ученого Жозефа Плато. Нечаянно он налил в смесь спирта и воды небольшое количество масла, и оно приняло форму шара. Плато, пожалуй, следует считать пионером этой науки. Он первый, оставаясь приверженным Земле, поставил жидкость в условия невесомости, «отключив» тяготение для одной капли.
Действие сил поверхностного натяжения, также используют в современных технологических устройствах.
Современная наука развивает с помощью капель нанотехнологию. Ученые лаборатории Белла в США, штат Нью-Джерси открыли способ управления поведением капель жидкости. Они изобрели наногазон.
Что же такое наногазон?
Это пластинка из кристаллов кремния, которая при большом увеличении напоминает аккуратно подстриженный газон. Он состоит из столбиков толщиной 200-300 нанометров, в тысячу раз тоньше, чем человеческий волос. У этого газона есть замечательное свойство: если на него поместить каплю жидкости, то она не будет растекаться, а останется шарообразной формы. Этот шарик может катиться по поверхности в любом направлении, которое нам нужно, но как только мы подадим на определенные “травинки” электрическое напряжение, то шарообразная капля начнет “протекать” в пространство между травинками. На одном таком микро устройстве можно создать целую химическую лабораторию. Внизу, у основания газона, ученые наносят различные реагенты. Далее они с помощью электрического импульса заставляют каплю просачиваться в тех местах, где нанесены реагенты, после чего начинают считывать с помощью оптических приборов результаты реакции. Это может быть изменение цвета или свечение. Таким образом, покатав по наногазону каплю человеческой крови, можно сделать ее полный биохимический анализ.
2.2 Практическая часть
«Изучение и наблюдение природы породило науку».
(Марк Туллий Цицерон)
Физика по-прежнему смотрит на каплю с интересом и интригой. В процессе работы мы рассмотрим образование капли, научимся определять её малую массу и объём, время её падения. Узнаем, как ведёт себя капля различных веществ на твёрдых поверхностях, поместим каплю в состояние невесомости в Земных условиях.
Объект исследования: капли жидкости
Предмет исследования: поведение капель жидкости в различных условиях
Методы исследования : наблюдение, эксперимент, анализ, обобщение.
Необходимо взять две бутылки (0,5л), затем первую бутылку нужно разрезать на две части (нам нужна часть с дном). Вторая бутылка нам необходима как емкость для хранения воды. У второй бутылки заменяем простую крышку на капельник от моющего средства (т. к. её форма предназначена для зарождения капли). После замены крышки необходимо во вторую бутылку налить воды. Следующее действие мы берем обрезанную бутылку и бутылку с жидкостью внутри и вторую бутылку вставляем в первую. Прибор для получения капель готов.
Для лучшего наблюдения капель можно использовать насыщенный водный раствор соли.
Опыт№1 Наблюдение за образованием капли: капля растет, образуется сужение – шейка и капля отрывается. Объяснение : вода как бы заключена в эластичный мешочек, и когда его прочность становится недостаточной для удержания большой массы воды, он разрывается. Эластичный мешочек – это поверхностный слой воды. Когда сила поверхностного натяжения становится меньше гравитационной силы, капля отрывается и падает.
2)Опыт №2 : « Определение массы капли воды и промежутка времени падения капли воды»
Цель работы : научиться измерять малые величины на примере определения массы и промежутка времени падения капли воды.
Приборы и материалы: Прибор для получения капель жидкости, сосуд известного объема (стакан с делениями, мерная посуда, банка или бутылка известного объема), вода, секундомер.
1.Возьмите сосуд известного объема (стакан с делениями, мерную посуду, банку или бутылку известного объема). Узнать, какую массу воды вмещает этот сосуд в граммах. Масса воды в сосуде – m1.
4. Рассчитайте массу m2 одной капли формуле m2 = m1/n в граммах.
5. Рассчитайте промежуток времени tо в секундах падения одной капли воды по формуле t2= t1/n
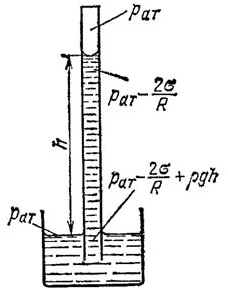
Чем обусловлена шарообразная форма капель
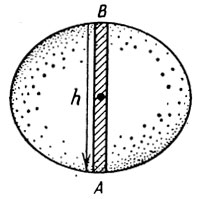
Мы привыкли думать, что жидкости не имеют никакой собственной формы. Это неверно. Естественная форма всякой жидкости – шар. Обычно сила тяжести мешает жидкости принимать эту форму, и жидкость либо растекается тонким слоем, если разлита без сосуда, либо же принимает форму сосуда, если налита в него. Находясь внутри другой жидкости такого же удельного веса, жидкость по закону Архимеда “теряет” свой вес: она словно ничего не весит, тяжесть на нее не действует – и тогда жидкость принимает свою естественную, шарообразную форму.
Прованское масло плавает в воде, но тонет в спирте. Можно поэтому приготовить такую смесь из воды и спирта, в которой масло не тонет и не всплывает. Введя в эту смесь немного масла посредством шприца, мы увидим странную вещь: масло собирается в большую круглую каплю, которая не вплывает и не тонет, а висит неподвижно [Чтобы форма шара не казалась искаженной, нужно производить опыт в сосуде с плоскими стенками (или в сосуде любой формы, но поставленном внутри наполненного водой сосуда с плоскими стенками)].


Опыт надо проделывать терпеливо и осторожно, иначе получится не одна большая капля, а несколько шариков поменьше. Но и в таком виде опыт достаточно интересен.
Это, однако, еще не все. Пропустив через центр жидкого масляного шара длинный деревянный стерженек или проволоку, вращают их. Масляный шар принимает участие в этом вращении. (Опыт удается лучше, если насадить на ось небольшой смоченный маслом картонный кружочек, который весь оставался бы внутри шара.) Под влиянием вращения шар начинает сначала сплющиваться, а затем через несколько секунд отделяет от себя кольцо. Разрываясь на части, кольцо это образует не бесформенные куски, а новые шарообразные капли, которые продолжают кружиться около центрального шара.
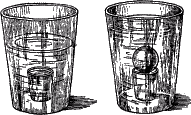
Впервые этот поучительный опыт произвел бельгийский физик Плато. Здесь описан опыт Плато в его классическом виде. Гораздо легче и не менее поучительно произвести его в ином виде. Маленький стакан споласкивают водой, наполняют прованским маслом и ставят на дно большого стакана; в последний наливают осторожно столько спирта, чтобы маленький стакан был весь в него погружен. Затем по стенке большого стакана из ложечки осторожно доливают понемногу воду. Поверхность масла в маленьком стакане становится выпуклой; выпуклость постепенно возрастает и при достаточном количестве подлитой воды поднимается из стакана, образуя шар довольно значительных размеров, висящий внутри смеси спирта и воды (рис. 58).
За неимением спирта можно проделать этот опыт с анилином – жидкостью, которая при обыкновенной температуре тяжелее воды, а при 75 – 85 °С легче ее. Нагревая воду, мы можем, следовательно, заставить анилин плавать внутри нее, причем он принимает форму большой шарообразной капли. При комнатной температуре капля анилина уравновешивается в растворе соли [Из других жидкостей удобен ортотолуидин – темно-красная жидкость; при 24° она имеет такую же плотность, как и соленая вода, в которую и погружают ортотолуидин].