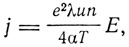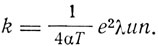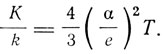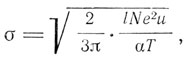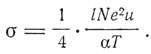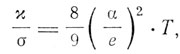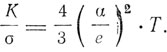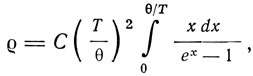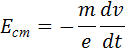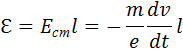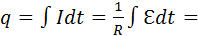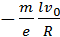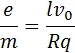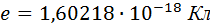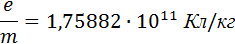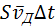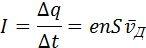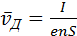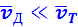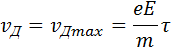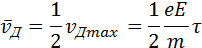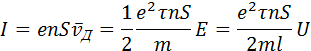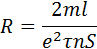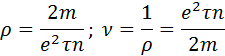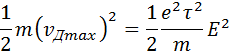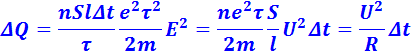Чем обусловлена электропроводность металлов

Чем обусловлена электропроводность металлов

Электропроводность металлов

Переходим теперь к рассмотрению электрических свойств твердого тела. Из этой области наибольшее развитие получила теория электропроводности металлов.

Уже в 1898 г. Э. Рикке предположил, что молекулы металла частично диссоциированы и в пространстве между молекулами имеются положительно и отрицательно заряженные частички. Поведение этих частиц определяется законами кинетической теории газов, однако плотность их настолько мала, что в расчет принимаются только их столкновения с молекулами металла, но не столкновения их между собой. Ток представляет упорядоченный поток этих частиц: положительно заряженных по направлению поля, отрицательно заряженных против поля. Существованием таких частиц Рикке объяснял и контактную разность потенциалов.

Рикке пытался выяснить, происходит ли перенос вещества в металлах током, обусловленным движением этих частиц. С этой целью он пропускал довольно сильный ток (около 10 ампер) в течение нескольких лет через цепь, составленную из кусков золота и серебра, плотно прилегающих друг к другу. Он не обнаружил никакого проникновения атомов золота в серебро и наоборот. Таким образом, носители электрического тока в металле являются не ионами, как в электролитах, а частицами, не связанными с массами обычных атомов.

В 1900 г. теорию электропроводности металлов развил Пауль Друде. Друде принимает, что электропроводность металлов обусловлена наличием свободных электронов. Однако наряду с отрицательными электронами он допускает и наличие положительных электронов, причем ток создается совместным направленным движением электронов обоего рода в противоположных направлениях. Друде применяет к электронам выводы классической теории газов (электронный газ) и принимает, что вследствие взаимных столкновений электронов между собой они в среднем получают одинаковую кинетическую энергию, пропорциональную абсолютной температуре

т. е. закон Ома: j = kE, где коэффициент электропроводности

Отсюда Друде находит соотношение между теплопроводностью К и электропроводностью k:

С помощью представления о свободных электронах Томсон получает объяснение термоэлектрических явлений (явления Пельтье и Томсона), а также явления Холла. Но в последнем случае встречается одно затруднение: явление Холла в различных веществах имеет разный знак. Друде обходил это затруднение, предполагая существование двух родов носителей тока: отрицательных и положительных. В зависимости от природы вещества в нем может преобладать либо ток отрицательного, либо ток положительного электричества (прообраз современной электронной и «дырочной» проводимости). Однако Томсон, принимая за носителей тока только отрицательно заряженные корпускулы, отклоняет эту теорию. Причину различия эффекта Холла он усматривает в неодинаковости действия магнитного поля на корпускулы во время их свободного движения и во время их столкновения. Последнее действие в зависимости от природы молекул может совпадать с действием на корпускулу при свободном движении, а может быть и прямо противоположным. Вместе с тем Томсон указывает, что применять образы кинетической теории газов к металлам следует с большой осторожностью; строение куска металла резко отличается от строения газов. «Кусок металла, по-видимому, представляет собой агрегат большого числа маленьких кристаллов»,- пишет Томсон.

Томсон останавливается также и на теории теплового излучения электронами, движущимися в металле. Эта теория была предложена Лоренцем и о ней говорилось в шестой главе.

По второй теории Томсона проводимость обусловлена переходом корпускулы вдоль цепочки поляризованных атомов от одного атома к другому. По этой теории отношение теплопроводности к электропроводности равно

В 1903 г. Г. А. Лоренц опубликовал статью «Об испускании и поглощении металлами тепловых лучей больших длин волн», на результаты которой и ссылается Д. Д. Томсон в своей теории проводимости в 1906 г. в книге «Корпускулярная теория материи». Выше мы приводили этот результат, который является не чем иным, как законом Рэлея-Джинса. В этой статье Лоренц исходит из теории проводимости Рикке-Друде и опытов Гагена и Рубенса 1903 г. по отражательной способности металлов для лучей длин волн более 8μ. Из этих опытов следует, что поведение металлов при отражении таких волн определяется только их проводимостью. Лоренц кратко излагает суть теории Друде и приводит его выражение для электропроводности, на которое он и опирается в последующих расчетах излучательной и поглощательной способности металлов. В 1905 г. Лоренц развивает дальше кинетическую теорию электропроводности, предполагая, что распределение тепловых скоростей электронов подчиняется закону Максвелла. Он получает при этом выражение для коэффициента электропроводности в виде

Закон Видемана-Франца в теории Лоренца имеет вид

Лоренц так же, как и Томсон, прилагает свою теорию к термоэлектрическим явлениям, объясняя и явление Пельтье, и явление Томсона.

Камнем преткновения для теории свободных электронов в металле было явление Холла, которое, как кажется, говорит в пользу гипотезы двух родов носителей тока. 17 апреля 1906 г. Лоренц прочитал лекцию «О положительных и отрицательных электронах» в Американском философском обществе в Филадельфии, основанном Б. Франклином. Разбирая гипотезу двух родов электричества, Лоренц приходит к выводу, что она противоречит второму закону термодинамики и, следовательно, электрический ток в металле обусловлен движением частиц одного рода, отрицательно заряженных электронов. Свою лекцию Лоренц заканчивает следующими словами: «Поскольку эффект Холла на первый взгляд кажется очень сильно благоприятствующим теории двух флюидов, мы должны исследовать, не может ли он быть объяснен движением только отрицательных электронов. Если мы преуспеем в этом, проникнув возможно глубже в механизм явления. то мы после всего придем к системе объяснения, значительно напоминающей франклинову унитарную теорию электричества».

Х. Каммерлинг-Оннес в своей лаборатории

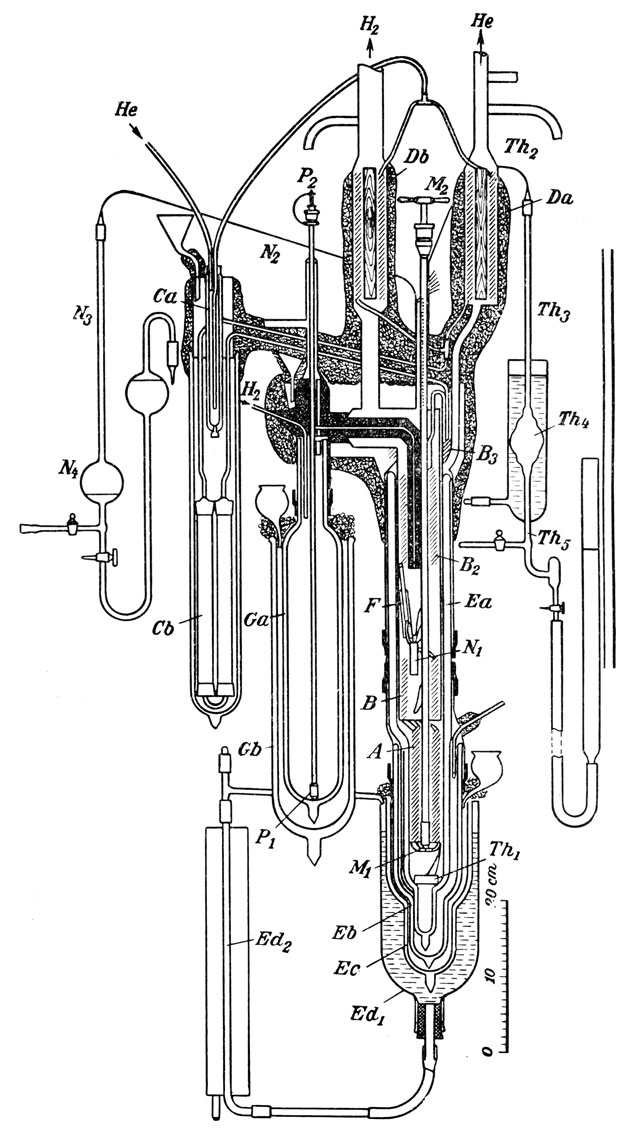
Гелиевый ожижитель Каммерлинг-Оннеса показан на рисунке. Жидкий водород непрерывно переливается сифоном из градуированного сосуда Ga. Гелий подавался компрессором под давлением 100 атмосфер и последовательно

Каммерлинг-Оннес получил с этим аппаратом при первом опыте 60 кубических сантиметров жидкого гелия.

Явление сверхпроводимости поставило теорию электронного газа перед чрезвычайными трудностями. Вин в 1913 г. пришел к выводу, что «электронная теория металла должна быть построена на существенно новой основе». Он предположил, что скорость свободных электронов совершенно не зависит от температуры. При правильной кристаллической решетке ее проводимость должна быть бесконечной, что соответствует опытам Каммерлинг-Оннеса. Тепловые колебания атомов нарушают эту правильность и сопротивление становится конечным. Столкновение электронов с атомами вещества производит поглощение или излучение кванта энергии. Рассчитывая сопротивление металла, Вин приходит к формуле

За год до публикации теории Томсона был опубликован в неоднократно упоминавшихся нами геттингенских докладах по теории материи и электричества доклад Г. А. Лоренца «Применение кинетической теории к движению электронов». Упомянув о теориях электропроводности Рикке, Друде и своей, в которых использовалось представление о свободных электронах со средней энергией 3 /₂kT, и об их успехах, Лоренц продолжал:

Схема аппарата для снижения гелия Каммерлинг-Оннеса

«Но постепенно им (т. е. этим теориям) стали противостоять значительные трудности, которые стимулировали предложение радикальных изменений. В недавно опубликованной работе (Лоренц имеет в виду появившуюся в 1913 г. работу Вина «К теории электрической проводимости в металлах») Вин идет даже так далеко, что полностью отказывается от представления о собственном тепловом движении, поскольку он приписывает электронам только скорость, не зависящую от температуры.» Вин исходил из того факта, что теория электронного газа приводит к неверному закону Рэлея для теплового излучения. В связи с этим Лоренц замечает, что тепловое излучение возникает в процессе изменения скорости электрона при столкновении с атомами металла. Но механизм столкновения электрона с атомом еще неясен, и Лоренц выражает надежду, «что квантовой теории, коль скоро она введет подходящие представления для механизма столкновения, когда-нибудь удастся добиться удовлетворительного объяснения теплового излучения».

Вместе с тем Лоренц приводит аргументы в пользу гипотезы о свободных электронах в металле, скорость которых зависит от температуры. Так, он указывает, что анализ поведения электрона в поле черного излучения, сделанный им на Сольвеевском конгрессе 1911 г. и Фоккером в диссертации 1913 г., показывает, что средняя кинетическая энергия электрона в этом поле действительно пропорциональна температуре, хотя коэффициент пропорциональности получается меньше 3 /₂ примерно в 24 раза. Он ссылается также на опыты Ричардсона по определению кинетической теории электронов, испускаемых нагретыми металлами, которые показывают, что находящиеся внутри металла свободные электроны обладают в среднем кинетической энергией 3 /₂kT. Тем самым доказывается, что электроны в металле участвуют в тепловом движении. Вместе с тем значение теплоемкости металла при обычных температурах указывает на незначительность вклада электронов в эту теплоемкость. Поэтому Лоренц предполагает, что число свободных электронов в металле очень незначительно по сравнению с числом атомов. Остальные электроны следует считать неподвижными или, во всяком случае, обладающими кинетической энергией, значительно меньшей, чем 3 /₂kT. Далее, Лоренц, ссылаясь на свою работу «О положительных и отрицательных электронах» (см. выше), указывает, что предположение о нескольких видах носителей тока противоречит второму закону термодинамики и что носителями тока являются только электроны. Он рассматривает затем механизм столкновения электронов с атомами. При этом он делает важное предположение, что электрон после столкновения покидает атом с той же скоростью, какой он обладал до столкновения. Направление же скорости остается совершенно неопределенным. Вполне возможно, что электрон при столкновении застревает в атоме, а взамен его атом испускает другой электрон с той же скоростью. Эта картина взаимодействия электронов с атомами напоминает позднейшие представления о столкновениях частиц с ядрами атомов.

Неопределенность направления скорости электронов после соударения приводит к тому, что в отличие от прежних теорий соотношение между теплопроводностью и электропроводностью металлов и зависимость этих величин от различных обстоятельств не могут быть указаны. Однако термоэлектрические величины должны удовлетворять соотношениям, выведенным из второго закона термодинамики. Лоренц исследует термоэлектрическую цепь сначала термодинамически, а затем прилагает к ней статистику Максвелла-Больцмана. При этом он приходит к выводу, что термодинамически полученное соотношение совпадает с соотношениями, выведенными из кинетической теории только в том случае, если для стационарного состояния справедлив закон распределения Максвелла. Вместе с тем для получения определенных значений характеристик металла, в частности коэффициента электропроводности, необходимы определенные допущения о механизме столкновения. Если воздержаться от таких допущений, то нельзя вывести и закон Видемана-Франца. Лоренц указывает, что посредством исследования соответствующих частных случаев можно даже показать, что этот закон вообще не справедлив и его следует рассматривать как приближенное правило.

Аппарат для сжижения гелия в лаборатории Каммерлинг-Оннеса в Лейдене

Свою статью Лоренц заканчивает любопытным примером. Он рассматривает электростатическую задачу о поле, создаваемом точечным зарядом, помещенным перед бесконечной проводящей плоскостью. Как известно, это поле совпадает с полем, произведенным данным зарядом и его «электрическим изображением» в плоскости. Заряд этого изображения распределен по плоскости с плотностью, убывающей обратно пропорционально третьей степени расстояния от центра. Но как будет выглядеть это распределение, если перед плоскостью помещен положительный заряд, равный элементарному заряду е? Лоренц указывает, что индуцированный отрицательный электрон будет быстро менять свое положение на плоскости и его распределение в среднем будет совпадать с распределением, даваемым электростатикой. Наблюдению доступно только это распределение. Это статистическое «распределение» электрона на поверхности было предшественником будущих статистических закономерностей квантовой механики.

Участвовавший в геттингенской дискуссии сотрудник Каммерлинга-Оннеса Биллем Гендрик Кеезом выступил с сообщением «О применении квантовой теории к теории свободных электронов в металле». Кеезом замечает, что квантовая теория может быть применена к свободным электронам в металлах таким же образом, как она была применена Тетроде и Ленцем к идеальному газу, если ввести дополнительно нулевую энергию. Поскольку в системе свободных электронов частоты, соответствующие скоростям электронов, значительно выше, чем частоты, появляющиеся для идеальных газов, следствия, получающиеся для идеальных газов при крайне низких температурах, будут применимы для электронов при экспериментально достигаемых температурах. Для высоких температур энергия свободных электронов совпадает с даваемой теорией Друде-Лоренца, но для низких температур энергия и, следовательно, средняя скорость приближаются к конечному постоянному значению, что соответствует предположению Вина в его теории электропроводности. Тем самым устраняются затруднения с теплоемкостью и нет необходимости принимать малое число свободных электронов. Число свободных электронов при низких температурах приближается к постоянному значению, как это принимает Вин в своей теории. Таким образом, применение квантовой теории, по Кеезому, дает результаты, согласующиеся при низких температурах с теорией Вина. В 1915 г. Лоренц, суммируя кратко положения электронной теории металлов, заключал: «Впрочем, в области, которой мы кратко коснулись, имеется еще много нерешенных проблем, из которых некоторые представляют значительные трудности, поскольку, как вообще должно быть признано, физические теории до настоящего времени проникли в сущность материи еще очень поверхностно».

Однако это проникновение в сущность материи уже началось и многие результаты электронной теории проводимости были только незначительно модифицированы квантовой теорией металлов, что, конечно, не означает недооценки глубокого принципиального значения изменений, внесенных в теорию проводимости квантовой теорией. На эту теорию, как мы видели, возлагал надежды и Лоренц.

Источник

Электрический ток в металлах

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л.И. Мандельштаму и Н.Д. Папалекси В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

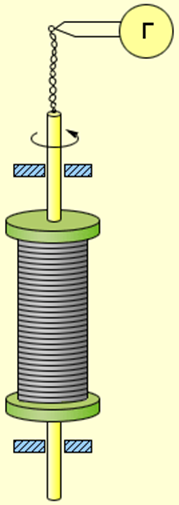
Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

Схема опыта Толмена и Стюарта

При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила 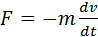которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E_ст поля сторонних сил:

Следовательно, в цепи при торможении катушки возникает электродвижущая сила 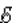, равная

где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный

Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ₀ – начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен:

Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд) равен

а его удельный заряд есть

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

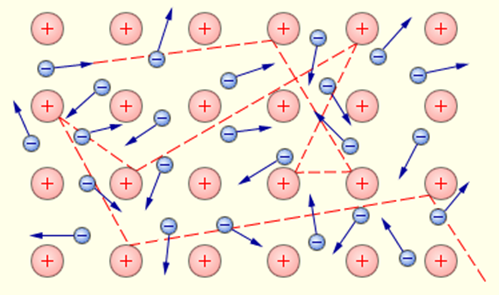
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.

Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость 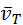теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость 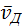дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме

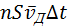
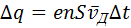
Число таких электронов равно , где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:

или

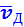
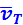
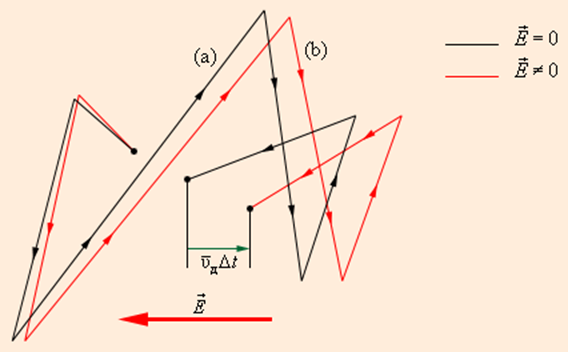
средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения

Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа 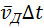сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение 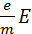. Поэтому к концу свободного пробега дрейфовая скорость электрона равна

где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа 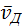равно половине максимального значения:

Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:

где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:

а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:

Закон Джоуля-Ленца.

К концу свободного пробега электроны под действием поля приобретают кинетическую энергию

Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.

За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:

Это соотношение выражает закон Джоуля-Ленца.

Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение 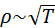, в то время как из эксперимента получается зависимость ρ

T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.

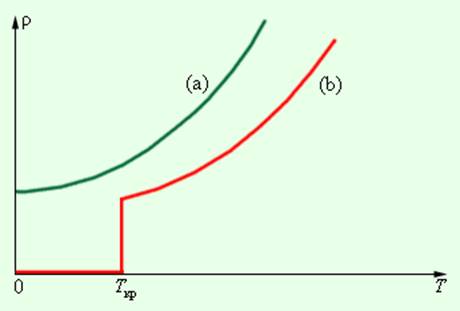
Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х.Каммерлинг-Онесом в 1911 году. При некоторой определенной температуре T_кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni₃Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник

Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.

Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения T_кр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.

В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями T_кр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Источник