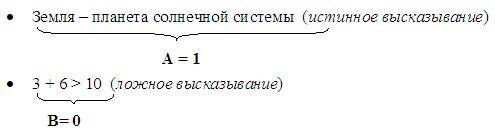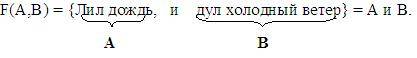Чем обозначаются высказывания в алгебре высказываний

Алгебра высказываний

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,

Многие люди не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

Пример:
Рассмотрим составное высказывание «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: \/, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.

Пример:
Рассмотрим составное высказывание «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.

Источник

АЛГЕБРА ВЫСКАЗЫВАНИЙ

АЛГЕБРА ВЫСКАЗЫВАНИЙ является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний – решение логических задач.

Объекты алгебры высказываний. Операции над высказываниями. Таблицы истинности.

Алгебра – это наука, которая изучает множество некоторых элементов и действия (операции) над ними. Если элементы алгебры – натуральные числа, а операции – сложение и умножение, то это алгебра натуральных чисел. Действия с направленными отрезками (векторами) изучает векторная алгебра.

Объектами алгебры высказываний являются высказывания. Высказывание – это истинное или ложное повествовательное предложение. Повествовательное предложение, в котором говорится об одном-единственном событии, называется простым высказыванием. Например, предложение «Луна – спутник Земли» есть простое высказывание, предложение «Не сорить!» не является высказыванием.

Высказывания обозначаются большими буквами латинского алфавита. Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.

Таблица 1

А	В	АВ
1	1	1
1	0	0
0	1	0
0	0	0

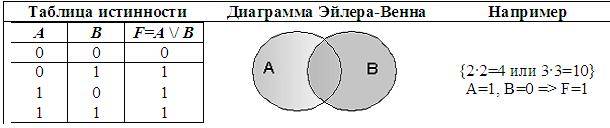
Объединение двух высказываний в одно с помощью союза «ИЛИ», употребляемого в неисключающем смысле, называется операцией логического сложения. Например, высказывание A – «Декабрь – зимний месяц», В – «Летом иногда идет дождь», определим высказывание A+B – «Декабрь – зимний месяц или летом иногда идет дождь». Установить истинность логической суммы можно с помощью следующей таблицы:

Таблица 2

А	В	А+В
1	1	1
1	0	1
0	1	1
0	0	0

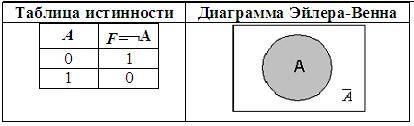
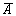
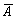
Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания (обозначается ) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Истинность высказывания определяется таблицей:

Таблица 3

А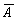
1	0
0	1

Пользуясь определенными выше операциями, можно из простых высказываний образовывать сложные. Например, всевозможные значения для высказывания 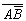можно записать в виде таблицы

Таблица 4

А	B		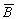A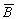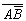
1	1	0	0	1
1	0	1	1	0
0	1	0	0	1
0	0	1	0	1

Тождественные высказывания. Эквивалентные высказывания. Формулы Августа де Моргана.

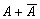
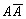
Среди высказываний особое место занимают те, в таблице истинности которых либо одни единицы, либо только нули. Это означает, что высказывание либо всегда истинно, либо ложно, независимо от истинности входящих в него высказываний. Например, высказывание всегда истинно, а высказывание всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.

Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.

Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:

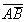
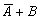
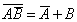
Среди высказываний встречаются такие, таблицы истинности которых совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания и (то есть ). Это можно проверить составив таблицы истинности этих высказываний:

Источник

MT1102: Линейная алгебра (введение в математику)

Определение высказываний

Высказывание — утверждение, относительно которого можно сказать истинно (1, истина, true) оно или ложно (0, ложь, false).

Примеры

Следующие предложения являются высказываниями:

%%A_1%%: «Лондон — столица Австрии».
%%A_2%%: «Число 8 больше числа 3».
%%A_3%%: «Число 8 больше числа 13».
%%A_4%%: «Луна — спутник планеты Земля».

Причем высказывания %%A_1, A_3%% — ложные, а %%A_2, A_4%% — истинные.

Следующие предложения не являются высказываниями:

%%B_1%%: «Какой сегодня день недели?».
%%B_2%%: «%%2 + 3%%».
%%B_3%%: «Число %%x%% больше 3».

Мы не можем сказать о любом из высказываний %%B_1, B_2, B_3%% истинно оно или ложно. Например, в предложении %%B_3%% буква %%x%% — переменная. Если поставить какое либо значение вместо нее, например 8, то получим истинное высказывание.

Операции над высказываниями

Пусть %%A%% и %%B%% — некоторые высказывания.

Конъюнкция

Конъюнкцией высказываний %%A%% и %%B%%

называется новое высказывание, обозначаемое %%A \land B%%, которое является истинным тогда и только тогда, когда высказывания %%A%% и %%B%% истины. Читается как %%A%% и %%B%%.

Рассмотрим конъюнкцию высказывний %%A_1%% и %%A_2%%, которая записывается как %%A_1 \land A_2%% и читается как «Генуя — столица Австрии и число 8 больше числа 3». Это высказывание ложно, так как высказывание %%A_1%% ложно. Другими словами, конъюнкция является ложной тогда и только тогда, когда хотя бы одно из высказываний ложно.

Рассмотрим произвольные высказывания %%A%% и %%B%% и полученное из них высказывание %%A \land B%%. Высказывания %%A, B%% могут быть как ложными, так и истинными. Возможны следующие варианты:

В каждом их этих случаев, вычислив значение конъюнкции высказываний %%A \land B%%, получим следующую таблицу, которая называется таблицей истинности.

%%A%%	%%B%%	%%A \land B%%
%%0%%	%%0%%	%%0%%
%%0%%	%%1%%	%%0%%
%%1%%	%%0%%	%%0%%
%%1%%	%%1%%	%%1%%

Где %%1%% обозначает истинное высказывание, %%0%% — ложное высказывание.

Дизъюнкция

Дизъюнкцией высказываний %%A%% и %%B%%

называется новое высказывание, обозначаемое %%A \lor B%%, которое является ложным тогда и только тогда, когда высказывания %%A%% и %%B%% ложны. Читается как %%A%% или %%B%%.

Рассмотрим дизъюнкцию высказывний %%A_1%% и %%A_2%%, которая записывается как %%A_1 \lor A_2%% и читается как «Москва — столица Австрии или число 8 больше числа 3». Это высказывание истинно, так как высказывание %%A_2%% истинно. Другими словами, дизъюнкция является истинной тогда и только тогда, когда хотя бы одно из высказываний истино.

Таблица истинности для дизъюнкции выглядит следующим образом.

%%A%%	%%B%%	%%A \lor B%%
%%0%%	%%0%%	%%0%%
%%0%%	%%1%%	%%1%%
%%1%%	%%0%%	%%1%%
%%1%%	%%1%%	%%1%%

Импликация

Импликацией высказываний %%A%% и %%B%% называется

новое высказывание, обозначаемое %%A \rightarrow B%%, которое является ложным тогда и только тогда, когда высказывание %%A%% истинно, %%B%% ложно. Читается как: «Если %%A%%, то %%B%%»; «%%A%% влечет %%B%%»; «из %%A%% следует %%B%%»; «%%A%% достаточно для %%B%%»; %%B%% необходимо для %%A%%».

Рассмотрим импликацию высказывний %%A_2%% и %%A_1%%, которая записывается как %%A_2 \rightarrow A_1%% и читается как «Если число %%8%% больше числа %%3%%, то Москва — столица Австрии». Это высказывание ложно, так как высказывание %%A_2%% истинно, а %%A_1%% ложно.

Таблица истинности для импликации выглядит следующим образом.

%%A%%	%%B%%	%%A \rightarrow B%%
%%0%%	%%0%%	%%1%%
%%0%%	%%1%%	%%1%%
%%1%%	%%0%%	%%0%%
%%1%%	%%1%%	%%1%%

Эквиваленция

Эквиваленцией высказываний %%A%% и %%B%%

называется новое высказывание, обозначаемое %%A \leftrightarrow B%%, которое является истинным тогда и только тогда, когда высказывание %%A%% и %%B%% одновременно истинны или ложны. Читается как: «%%A%% равносильно %%B%%»; «%%A%% необходимо и достаточно для %%B%%»; «%%A%% тогда и только тогда, когда %%B%%».

Рассмотрим импликацию высказывний %%A_1%% и %%A_2%%, которая записывается как %%A_1 \leftrightarrow A_2%% и читается как «Москва — столица Австрии тогда и только тогда, когда число %%8%% больше числа %%3%%». Это высказывание ложно, так как высказывание %%A_2%% истинно, а %%A_1%% ложно.

Таблица истинности для эквиваленции выглядит следующим образом.

%%A%%	%%B%%	%%A \leftrightarrow B%%
%%0%%	%%0%%	%%1%%
%%0%%	%%1%%	%%0%%
%%1%%	%%0%%	%%0%%
%%1%%	%%1%%	%%1%%

Также эквиваленцию можно выразить через импликацию и конъюнкцию, тогда

Покажем это, используя таблицы истинности.

%%A%%	%%B%%	%%A \leftrightarrow B%%	%%A \rightarrow B%%	%%B \rightarrow A%%	%%(A \rightarrow B) \land (B \rightarrow A)%%
%%0%%	%%0%%	%%1%%	%%1%%	%%1%%	%%1%%
%%0%%	%%1%%	%%0%%	%%1%%	%%0%%	%%0%%
%%1%%	%%0%%	%%0%%	%%0%%	%%1%%	%%0%%
%%1%%	%%1%%	%%1%%	%%1%%	%%1%%	%%1%%

Как видно из таблицы истинности столбцы %%A \leftrightarrow B%% и %%(A \rightarrow B) \land (B \rightarrow A)%% имеют одни и те же значения при одинаковых наборах значений %%A%% и %%B%%, что говорит о равенстве этих двух формул.

Отрицание

Отрицанием высказывания %%A%%

Рассмотрим отрицание высказывния %%A_1%%, которое записывается как %%\overline%% и читается как «неверно, что Москва — столица Австрии». Это высказывание истинно, так как высказывание %%A_1%% ложно.

Таблица истинности для отрицания выглядит следующим образом.

Источник

Основы алгебры логики

Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.

Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.

Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».

Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.

Это определение не является математически точным.

Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.

Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.

Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »

Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.

Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.

Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.

Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.

Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.

В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.

Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:

Источник

Чем обозначаются высказывания в алгебре высказываний

Простые и сложные высказывания, логиче­ские переменные и логические константы, логическое отрицание, логическое умноже­ние, логическое сложение, таблицы истин­ности для логических операций

Для описания рассуждений и правил выполне­ния действий с информацией используют специаль­ный язык, принятый в математической логике. В осно­ве рассуждений содержатся специальные предложе­ния, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объ­ектах, их свойствах и отношениях между объекта­ми. Высказыванием является любое суждение, отно­сительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повест­вовательные предложения. Вопросительные или по­будительные предложения высказываниями не явля­ются.

Высказывание — суждение, сформулированное в виде по­вествовательного предложения, о котором можно сказать, истинно оно или ложно.

Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предло­жение «Соблюдайте правила техники безопасности в компью­терном классе» высказываниями не являются. Повествователь­ные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство являет­ся внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются выска­зываниями, поскольку это суждения, о каждом из которых мож­но сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».

Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логиче­скими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве кото­рых используются заглавные латинские буквы. Логические пере­менные могут принимать только одно из двух возможных значе­ний: «истина» или «ложь». Например, высказывание «Информа­ция в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Прин­тер является устройством хранения информации» можно обо­значить логической переменной В. Поскольку первое выска­зывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказы­вание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.

Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.

Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.

Все рассуждения человека, а также работа современных тех­нических устройств основываются на типовых действиях с ин­формацией — трех логических операциях: логическом отрица­нии (инверсии), логическом умножении (конъюнкции) и логи­ческом сложении (дизъюнкции).

Логическое отрицание простого высказывания получают до­бавлением слов «Неверно, что» в начале простого высказывания.

■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы уме­ют летать». Результатом логического отрицания будет высказы­вание «Неверно, что крокодилы умеют летать». Значение ис­ходного высказывания — «ложь», а значение нового — «истина».

■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказы­вание «Неверно, что файл должен иметь имя». Значение исход­ного высказывания — «истина», а значение нового высказыва­ния — «ложь».

Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, ло­гическое отрицание высказывания ложно, когда исходное вы­сказывание истинно.

Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значе­нию исходного высказывания.

Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логичес­кого отрицания (табл. 40).

ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ

Если/1 = 0, то НЕ А = 1 (см. пример 1).

Если А = 1, то НЕ А = 0 (см. пример 2)

Можно заметить, что в таблице истинности для логическо­го отрицания ноль меняется на единицу, а единица меняется на ноль.

Логическое умножение двух простых высказываний получа­ют объединением этих высказываний с помощью союза и. Разбе­рем на примерах 3—6, что будет являться результатом логическо­го умножения.

■ ПРИМЕР 3. Имеются два простых высказывания. Одно выска­зывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».

Результатом логического умножения этих простых высказы­ваний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение но­вого сложного высказывания также «ложь».

■ ПРИМЕР 4. Имеются два простых высказывания. Первое вы­сказывание — «Карлсон живет в подвале». Второе высказыва­ние — «Карлсон лечится вареньем».

Результатом логического умножения этих простых выска­зываний будет сложное высказывание «Карлсон живет в подва­ле и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».

■ ПРИМЕР 5. Имеются два простых высказывания. Первое вы­сказывание — «Карлсон живет на крыше». Второе высказыва­ние — «Карлсон лечится мороженым».

Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».

Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».

Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.

Логическое умножение (конъюнкция) — логическая опера­ция, ставящая в соответствие двум простым высказывани­ям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.

ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ

Источник