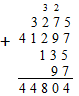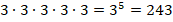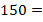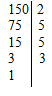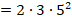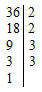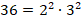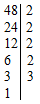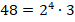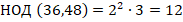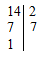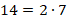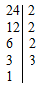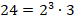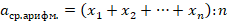Чем обозначаются натуральные числа

Натуральные числа. Ряд натуральных чисел.

История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.

Натуральные числа – это числа которые мы используем при счете предметов.

Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….

Нуль не относится к натуральным числам.

Все натуральные числа или назовем множество натуральных чисел обозначается символом N.

Таблица натуральных чисел.

Натуральный ряд.

Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.

Свойства натурального ряда:

Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5

Пример №2:
Нуль является натуральным числом?
Ответ: нет.

Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.

Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.

Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.

Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.

Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.

Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.

Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.

Источник

Натуральные числа

Содержание

Определение натуральных чисел [ править ]

Неформальное определение [ править ]

Определение:

Натура́льные чи́сла (англ. natural numbers, естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).

Существуют два подхода к определению натуральных чисел — числа, используемые при:

Отрицательные и нецелые числа натуральными числами не являются.

Формальное определение [ править ]

Определить множество натуральных чисел позволяют аксиомы Пеано (англ. Peano axioms):

Теоретико-множественное определение [ править ]

Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.

Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:

Числа, заданные таким образом, называются ординальными.

Первые несколько ординальных чисел и соответствующие им натуральные числа:

Классы эквивалентности этих множеств относительно биекций также обозначают [math]0, 1, 2, \dots.[/math]

Перечисленные аксиомы отражают наше интуитивные представления о «натуральном ряде».

Операции над натуральными числами [ править ]

Сложение [ править ]

Умножение [ править ]

Вычитание [ править ]

Деление чисел с остатком [ править ]

Формула деления с остатком: [math]n = m \cdot k + r,[/math] где [math]n\,[/math] — делимое, [math]m\,[/math] — делитель, [math]k\,[/math] — частное, [math]r\,[/math] — остаток, причем [math]0\leqslant r \lt b [/math]

Основная теорема арифметики [ править ]

Лемма Евклида [ править ]

Основная теорема арифметики [ править ]

Существование. Пусть [math]n[/math] — наименьшее натуральное число, неразложимое в произведение простых чисел. Оно не может быть единицей по формулировке теоремы. Оно не может быть и простым, потому что любое простое число является произведением одного простого числа — себя. Если [math]n[/math] составное, то оно — произведение двух меньших натуральных чисел. Каждое из них можно разложить в произведение простых чисел, значит, [math]n[/math] тоже является произведением простых чисел. Противоречие.

Принцип индукции, существование наименьшего числа в любом множестве натуральных чисел [ править ]

Индукция [ править ]

Формулировка принципа математической индукции:

Верность этого метода доказательства вытекает из так называемой аксиомы индукции, пятой из аксиом Пеано, которые определяют натуральные числа. Рассмотрение аксиом Пеано выходит за рамки этой статьи.

Также существует принцип полной математической индукции. Вот его строгая формулировка:

Существование наименьшего элемента [ править ]

Аксиому индукции можно заменить на аксиому существования минимума, и доказать аксиому индукции как теорему.

Из этой теоремы вытекает следующее утверждение, эквивалентное аксиоме математической индукции, но иногда более удобное при проведении доказательств.

Источник

Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.

Общее представление о натуральных числах

На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.

Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.

Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.

Десятичная запись натурального числа

Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.

Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.

Количественный смысл натуральных чисел

Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.

Далее, по аналогии: Ψ Ψ Ψ – 3 предмета («три»), Ψ Ψ Ψ Ψ – 4 («четыре»), Ψ Ψ Ψ Ψ Ψ – 5 («пять»), Ψ Ψ Ψ Ψ Ψ Ψ – 6 («шесть»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 7 («семь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 8 («восемь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 9 («девять»).

С указанной позиции функция натурального числа заключается в указании количества предметов.

Однозначные натуральные числа

Однозначное натуральное число – натуральное число, при записи которого используется один знак – одна цифра.

Двузначные и трехзначные натуральные числа

Двузначные натуральные числа – натуральные числа, при записи которых используются два знака – две цифры. При этом используемые цифры могут быть как одинаковые, так и различные.

Рассмотрим, какой смысл заключен в двузначных числах. Опираться будем на уже известный нам количественный смысл однозначных натуральных чисел.

Введем такое понятие как «десяток».

Представим множество предметов, которое состоит из девяти и еще одного. В таком случае можно говорить об 1 десятке («один десяток») предметов. Если представить один десяток и еще один, то речь пойдёт о 2 десятках («два десятка»). Прибавив к двум десяткам еще один, получим три десятка. И так далее: продолжая добавлять по одному десятку, мы будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков и, наконец, девять десятков.

Трехзначные натуральные числа – натуральные числа, при записи которых используются три знака – три цифры. Цифры могут быть различными или повторяющимися в любом сочетании.

Чтобы понять количественный смысл трехзначных натуральных чисел, введем понятие «сотня».

Одна сотня ( 1 сотня) – это множество, состоящее из десяти десятков. Сотня и еще одна сотня составят 2 сотни. Прибавим еще одну сотню и получим 3 сотни. Добавляя постепенно по одной сотне, получим: четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен.

Так, трехзначное натуральное число 402 обозначает: 2 единицы, 0 десятков (отсутствуют десятки, не объединенные в сотни) и 4 сотни.

По аналогии дается определение четырёхзначных, пятизначных и так далее натуральных чисел.

Многозначные натуральные числа

От всего вышесказанного теперь возможно перейти к определению многозначных натуральных чисел.

Многозначные натуральные числа – натуральные числа, при записи которых используются два и более знаков. Многозначные натуральные числа – это двухзначные, трехзначные и так далее числа.

Одна тысяча – множество, включающее в себя десять сотен; один миллион состоит из тысячи тысяч; один миллиард – тысяча миллионов; один триллион – тысяча миллиардов. Еще более крупные множества также имеют названия, но использование их редко.

Аналогично принципу выше, мы можем рассмотреть любое многозначное натуральное число, как набор однозначных натуральных чисел, каждое из которых, находясь на определенном месте, свидетельствует о наличии и количестве единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов и так далее (справа налево соответственно).

Например, многозначное число 4 912 305 содержит в себе: 5 единиц, 0 десятков, три сотни, 2 тысячи, 1 десяток тысяч, 9 сотен тысяч и 4 миллиона.

Резюмируя, мы рассмотрели навык группировки единиц в различные множества (десятки, сотни и т.д.) и увидели, что цифры в записи многозначного натурального числа являются обозначением количества единиц в каждом из таких множеств.

Чтение натуральных чисел, классы

В теории выше мы обозначили названия натуральных чисел. В таблице 1 укажем, как верно использовать названия однозначных натуральных чисел в речи и при буквенной записи:

Один
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять

Одна
Две
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять

Одно
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять

Теорема (О существовании минимума):

Число	Именительнный падеж	Родительный падеж	Дательный падеж	Винительный падеж	Творительный падеж	Предложный падеж
1 2 3 4 5 6 7 8 9	Один Два Три Четыре Пять Шесть Семь Восемь Девять	Одного Двух Трех Четырех Пяти Шести Семи Восьми Девяти	Одному Двум Трем Четырем Пяти Шести Семи Восьми Девяти	Один Два Три Четыре Пять Шесть Семь Восемь Девять	Одним Двумя Тремя Четырьмя Пятью Шестью Семью Восьмью Девятью	Об одном О двух О трех О четырех О пять О шести О семи О восьми О девяти

Для грамотного прочтения и написания двузначных чисел, необходимо выучить данные таблицы 2 :

Мужской, женский и средний род

10
11
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90Десять
Одиннадцать
Двенадцать
Тринадцать
Четырнадцать
Пятнадцать
Шестнадцать
Семнадцать
Восемнадцать
Девятнадцать
Двадцать
Тридцать
Сорок
Пятьдесят
Шестьдесят
Семьдесят
Восемьдесят
Девяносто

Десяти
Одиннадцати
Двенадцати
Тринадцати
Четырнадцати
Пятнадцати
Шестнадцати
Семнадцати
Восемнадцати
Девятнадцати
Двадцати
Тридцати
Сорока
Пятидесяти
Шестидесяти
Семидесяти
Восьмидесяти
Девяноста

Число	Именительнный падеж	Родительный падеж	Дательный падеж	Винительный падеж	Творительный падеж	Предложный падеж
10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90	Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто	Десяти Одиннадцати Двенадцати Тринадцати Четырнадцати Пятнадцати Шестнадцати Семнадцати Восемнадцати Девятнадцати Двадцати Тридцати Сорока Пятидесяти Шестидесяти Семидесяти Восьмидесяти Девяноста	Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто	Десятью Одиннадцатью Двенадцатью Тринадцатью Четырнадцатью Пятнадцатью Шестнадцатью Семнадцатью Восемнадцатью Девятнадцатью Двадцатью Тридцатью Сорока Пятидесятью Шестидесятью Семидесятью Восьмидесятью Девяностью	О десяти Об одиннадцати О двенадцати О тринадцати О четырнадцати О пятнадцати О шестнадцати О семнадцати О восемнадцати О девятнадцати О двадцати О тридцати О сорока О пятидесяти О шестидесяти О семидесяти О восьмидесяти О девяноста

Для того, чтобы читать трёхзначные числа, изучим данные таблицы 3 :

Сто
Двести
Триста
Четыреста
Пятьсот
Шестьсот
Семьсот
Восемьсот
Девятьсот

Число	Именительный падеж	Родительный падеж	Дательный падеж	Винительный падеж	Творительный падеж	Предложный падеж
100 200 300 400 500 600 700 800 900	Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот	Ста Двухсот Трехсот Четырехсот Пятисот Шестисот Семисот Восьмисот Девятисот	Ста Двумстам Тремстам Четыремстам Пятистам Шестистам Семистам Восьмистам Девятистам	Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот	Ста Двумстами Тремстами Четыремстами Пятистами Шестистами Семистами Восьмистами Девятистами	О ста О двухстах О трехстах О четырехстах О пятистах О шестистах О семистах О восьмистах О девятистах

Чтобы легко прочитать указанные натуральные числа, занесем их в таблицу:

Класс триллионов	Класс миллиардов	Класс миллионов	Класс тысяч	Класс единиц
134	678
31	013	736
23	476	009	434
2	533	467	001	222

Разберем подробно чтение числа 2 533 467 001 222 :

— добавив название класса, получим: «два триллиона»;

— читаем следующее число, добавив название соответствующего класса: «пятьсот тридцать три миллиарда»;

— продолжаем по аналогии, зачитывая следующий класс правее: «четыреста шестьдесят семь миллионов»;

— читаем последний класс единиц, не добавляя его название – «двести двадцать два».

Таким образом, число 2 533 467 001 222 будет звучать так: два триллиона пятьсот тридцать три миллиарда четыреста шестьдесят семь миллионов одна тысяча двести двадцать два. Используя указанный принцип, прочтем и прочие заданные числа:

— 31 013 736 – тридцать один миллион тринадцать тысяч семьсот тридцать шесть;

— 134 678 – сто тридцать четыре тысячи шестьсот семьдесят восемь;

— 23 476 009 434 – двадцать три миллиарда четыреста семьдесят шесть миллионов девять тысяч четыреста тридцать четыре.

Таким образом, основой правильного прочтения многозначных чисел является навык разбивать многозначное число на классы, знание соответствующих названий и понимание принципа прочтения двух- и трехзначных чисел.

Разряды натурального числа, значение разряда

Как уже становится понятно из всего вышесказанного, от позиции, на которой стоит цифра в записи числа, зависит ее значение. Т.е., например, цифра 3 в составе натурального числа 314 обозначает количество сотен, а именно – 3 сотни. Цифра 2 – количество десятков ( 1 десяток), а цифра 4 – количество единиц ( 4 единицы). При этом мы будем говорить, что цифра 4 находится в разряде единиц и является значением разряда единиц в заданном числе. Цифра 1 стоит в разряде десятков и служит значением разряда десятков. Цифра 3 располагается в разряде сотен и является значением разряда сотен.

Разряд – это позиция цифры в записи натурального числа, а также и значение этой цифры, которое определяется ее позицией в заданном числе.

Разряды имеют свои названия, мы уже использовали их выше. Справа налево следуют разряды: единиц, десятков, сотен, тысяч, десятков тысяч и т.д.

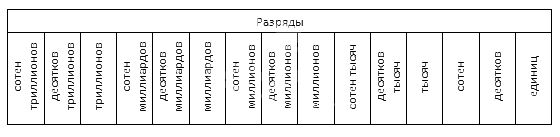
Для удобства запоминания можно использовать следующую таблицу (укажем 15 разрядов):

Уточним такую деталь: количество разрядов в заданном многозначном числе такое же, как количество знаков в составе записи числа. К примеру, данная таблица содержит названия всех разрядов для числа, в котором 15 знаков. Последующие разряды также имеют названия, но используются крайне редко и очень неудобны для восприятия на слух.

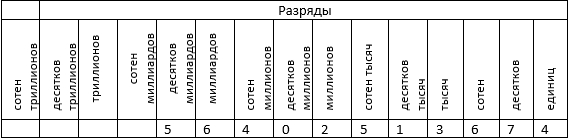
При помощи такой таблицы возможно наработать навык определения разряда, записывая заданное натуральное число в таблицу так, чтобы крайняя правая цифра была записана в разряде единиц и далее – в каждый разряд по цифре. К примеру, запишем многозначное натуральное число 56 402 513 674 так:

Введем также еще понятия низшего и высшего разрядов многозначного числа.

Низший (младший) разряд любого многозначного натурального числа – разряд единиц.

Высший (старший) разряд любого многозначного натурального числа – разряд, соответствующий крайней левой цифре в записи заданного числа.

Так, например, в числе 41 781 : низший разряд – разряд единиц; высший разряд – разряд десятков тысяч.

Логически следует, что возможно говорить о старшинстве разрядов относительно друг друга. Каждый последующий разряд при движении слева направо ниже (младше) предыдущего. И наоборот: при движении справа налево каждый следующий разряд выше (старше) предыдущего. К примеру, разряд тысяч старше разряда сотен, но младше разряда миллионов.

Уточним, что при решении некоторых практических примеров используется не само натуральное число, а сумма разрядных слагаемых заданного числа.

Кратко о десятичной системе счисления

Система счисления – метод записи чисел при помощи знаков.

Позиционные системы счисления – такие, в которых значение цифры в составе числа зависит от ее позиции в записи числа.

Помимо нее, существуют и прочие системы счисления. Например, информатика использует двоичную систему. Когда же мы ведем счет времени, то задействуем шестидесятеричную систему счисления.

Источник

Натуральные числа

Натуральные числа: определение, операции, свойства

Определение

Натуральными числами называются числа, предназначенные для счета предметов. Для записи натуральных чисел используются 10 арабских цифр (0–9), положенных в основание общепринятой для математических расчетов десятичной системы счисления.

Последовательность натуральных чисел

Иногда в ряд натуральных чисел вводят и 0. Это допустимо, и тогда говорят о расширенном натуральном ряде.

Классы натуральных чисел

Каждая цифра натурального числа выражает определенный разряд. Самая последняя – это всегда количество единиц в числе, предыдущая перед ней – количество десятков, третья от конца – количество сотен, четвертая – количество тысяч и так далее.

Для больших и очень больших чисел можно увидеть устойчивую тенденцию (если исследовать число справа налево, то есть от последней цифры к первой):

То есть всякий раз мы имеем дело с тремя цифрами, означающими единицы, десятки и сотни более крупного наименования. Такие группы формируют классы. И если с первыми тремя классами в повседневной жизни приходится иметь дело более или менее часто, то другие следует перечислить, потому что далеко не все помнят наизусть их названия.

Сложение натуральных чисел

Сложение натур.чисел представляет собой арифметическое действие, позволяющее получить число, в котором содержится столько же единиц, сколько имеется в складываемых числах вместе.

Знаком сложения является знак «+». Складываемые числа называются слагаемыми, получаемый результат – суммой.

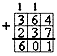
Небольшие числа складывают (суммируют) устно, письменно такие действия записывают в строку.

Если в столбик складывается не 2, а больше чисел, то при суммировании цифр разряда избыточным может оказаться не 1 десяток, а несколько. В этом случае на следующий разряд переносится количество таких десятков.

Вычитание натуральных чисел

Вычитание – это арифметическое действие, обратное сложению, которое сводится к тому, что по имеющейся сумме и одному из слагаемых нужно найти другое – неизвестное слагаемое. Число, из которого вычитают, называется уменьшаемым; число, которое вычитают, – вычитаемым. Результат вычитания называют разностью. Знак, которым обозначают действие вычитания, является «–».

При переходе к сложению вычитаемое и разность превращаются в слагаемые, а уменьшаемое – в сумму. Сложением обычно проверяют правильность выполненного вычитания, и наоборот.

Здесь 74 – уменьшаемое, 18 – вычитаемое, 56 – разность.

Обязательным условием при вычитании натуральных чисел является следующее: уменьшаемое обязательно должно быть больше вычитаемого. Только в этом случае полученная разность тоже будет натуральным числом. Если действие вычитания осуществляется для расширенного натурального ряда, то допускается, чтобы уменьшаемое было равно вычитаемому. И результатом вычитания в этом случае будет 0.

Примечание: если нулю равно вычитаемое, то операция вычитания не изменяет величины уменьшаемого.

Вычитание многозначных чисел обычно производят в столбик. Записывают при этом числа так же, как и для сложения. Вычитание выполняется для соответствующих разрядов. Если же оказывается, что уменьшаемое меньше вычитаемого, то берут единицу из предыдущего (находящегося слева) разряда, которая после переноса, естественно, превращается в 10. Эту десятку суммируют с цифрой уменьшаемого данного разряда и после этого производят вычитание. Далее при вычитании следующего разряда обязательно учитывают, что уменьшаемое стало на 1 меньше.

Произведение натуральных чисел

Произведение (или умножение) натуральных чисел – это арифметическое действие, представляющее собой нахождение суммы произвольного количества одинаковых слагаемых. Для записи действия умножения используют знак «·» (иногда «×» или «*»). Например: 3·5=15.

Действие умножение незаменимо при необходимости складывать большое количество слагаемых. Например, если нужно число 4 прибавить 7 раз, то перемножить 4 на 7 проще, нежели выполнять такое сложение: 4+4+4+4+4+4+4.

Числа, которые перемножают, называются множителями, результат умножения – произведением. Соответственно, термин «произведение» может в зависимости от контекста выражать собой как процесс умножения, так и его результат.

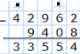
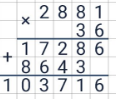
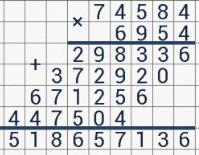
Многозначные числа перемножают в столбик. Для этого числа записывают так же, как и для сложения и вычитания. Рекомендуется первым (выше) записывать то из 2-х чисел, которое длиннее. В этом случае процесс умножения будет более простым, а следовательно, более рациональным.

При умножении в столбик выполняют последовательное умножение цифры каждого из разрядов второго числа на цифры 1-го числа, начиная с его конца. Найдя первое такое произведение, записывают цифру единиц, а цифру десятков держат в уме. При умножения цифры 2-го числа на следующую цифру 1-го числа к произведению прибавляют ту цифру, которую держат в уме. И снова записывают цифру единиц полученного результата, а цифру десятков запоминают. При умножении на последнюю цифру 1-го числа полученное таким способом число записывают полностью.

Результаты умножения цифры 2-го разряда второго числа записывают вторым рядом, сместив его на 1 клетку вправо. И так далее. В итоге будет получена «лесенка». Все получившиеся ряды цифр следует сложить (по правилу сложения в столбик). Пустые клетки при этом нужно считать заполненными нулями. Полученная сумма и есть конечное произведение.

Примечание

Деление натуральных чисел

Делением называют арифметическое действие, с помощью которого по известному произведению и одному из множителей может быть найдет другой – неизвестный – множитель. Деление является действием, обратным умножению, и используется для проверки правильности выполненного умножения (и наоборот).

Число, которое делят, называют делимым; число, на которое делят, – делителем; результат деления называется частным. Знаком деления является «:» (иногда, реже – «÷»).

Здесь 48 – делимое, 6 – делитель, 8 – частное.

Не все натуральные числа можно поделить между собой. В этом случае выполняют деление с остатком. Заключается оно в том, что для делителя подбирается такой множитель, чтобы его произведение на делитель было бы числом, максимально близким по значению к делимому, но меньшим него. Делитель умножают на этот множитель и вычитают его из делимого. Разность и будет остатком от деления. Произведение делителя на множитель называют неполным частным. Внимание: остаток обязательно должен быть меньше подобранного множителя! Если остаток больше, то это означает, что множитель подобран неверно, и его следует увеличить.

где a – перемножаемое само на себя число, x – количество таких множителей.

Простые и составные натуральные числа

Всякое натуральное число, кроме 1, можно разделить как минимум на 2 числа – на единицу и на само себя. Исходя из этого критерия, натуральные числа разделяют на простые и составные.

Простыми считаются числа, которые делятся только на 1 и на само себя. Числа, которые делятся более чем на эти 2 числа, называют составными. Единица, делящаяся исключительно на саму себя, не относится ни к простым, ни к составным.

Простыми являются числа: 2,3,5,7,11,13,17,19 и т.д. Примеры составных чисел: 4 (делится на 1,2,4), 6 (делится на 1,2,3,6), 20 (делится на 1,2,4,5,10,20).

Всякое составное число можно разложить на простые множители. Под простыми множителями при этом понимаются его делители, являющиеся простыми числами.

Пример разложения на простые множители:

Делители натуральных чисел

Под делителем понимают число, на которое можно без остатка разделить данное число.

В соответствии с этим определением, простые натур.числа имеют 2 делителя, составные – больше 2 делителей.

Многие числа имеют общие делители. Общим делителем называется число, на которое данные числа делятся без остатка.

Особое значение имеет наибольший общий делитель (НОД). Это число, в частности, полезно уметь находить для сокращения дробей. Для его нахождения требуется разложить данные числа на простые множители и представить его как произведение их общих простых множителей, взятых в наименьших своих степенях.

Требуется найти НОД чисел 36 и 48.

Делимость натуральных чисел

Далеко не всегда представляется возможным «на глазок» определить, делится ли одно число на другое без остатка. В таких случаях полезным оказывается соответствующий признак делимости, то есть правило, по которому за считанные секунды можно определить, можно ли разделить числа без остатка. Для обозначения делимости используется знак «».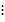

Наименьшее общее кратное

Эта величина (обозначается НОК) представляет собой наименьшее число, которое делится на каждое из заданных. НОК может быть найден для произвольного набора натуральных чисел.

НОК, как и НОД, имеет значительный прикладной смысл. Так, именно НОК нужно находить, приводя обыкновенные дроби к общему знаменателю.

НОК определяется путем разложения заданных чисел на простые множители. Для его формирования берется произведение, состоящее из каждого из встречающихся (хотя бы для 1 числа) простых множителей, представленных в максимальной степени.

Требуется найти НОК чисел 14 и 24.

Среднее арифметическое

Средним арифметических произвольного (но конечного) количества натуральных чисел является сумма всех этих чисел, разделенная на количество слагаемых:

Среднее арифметическое представляет собой некоторое усредненное значение для числового множества.

Даны числа 2,84,53,176,17,28. Требуется найти их среднее арифметическое.

Источник